Complete Solutions to Unsolved Numerical Problem of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| PHYSICS GALAXY | Unsolved Numerical Problem |
| Number Of Questions | 81 |
| Academic Year | 2023-24 |
A packet of 150kg is released from an air plane travelling due east at an altitude of 7200 m with a ground speed of 100 m/s. The wind applies a constant force on the packet of 300 N directed horizontally in the opposite direction to the plane's flight path. Where and when does the packet hit the ground, (with respect to the release location and time)
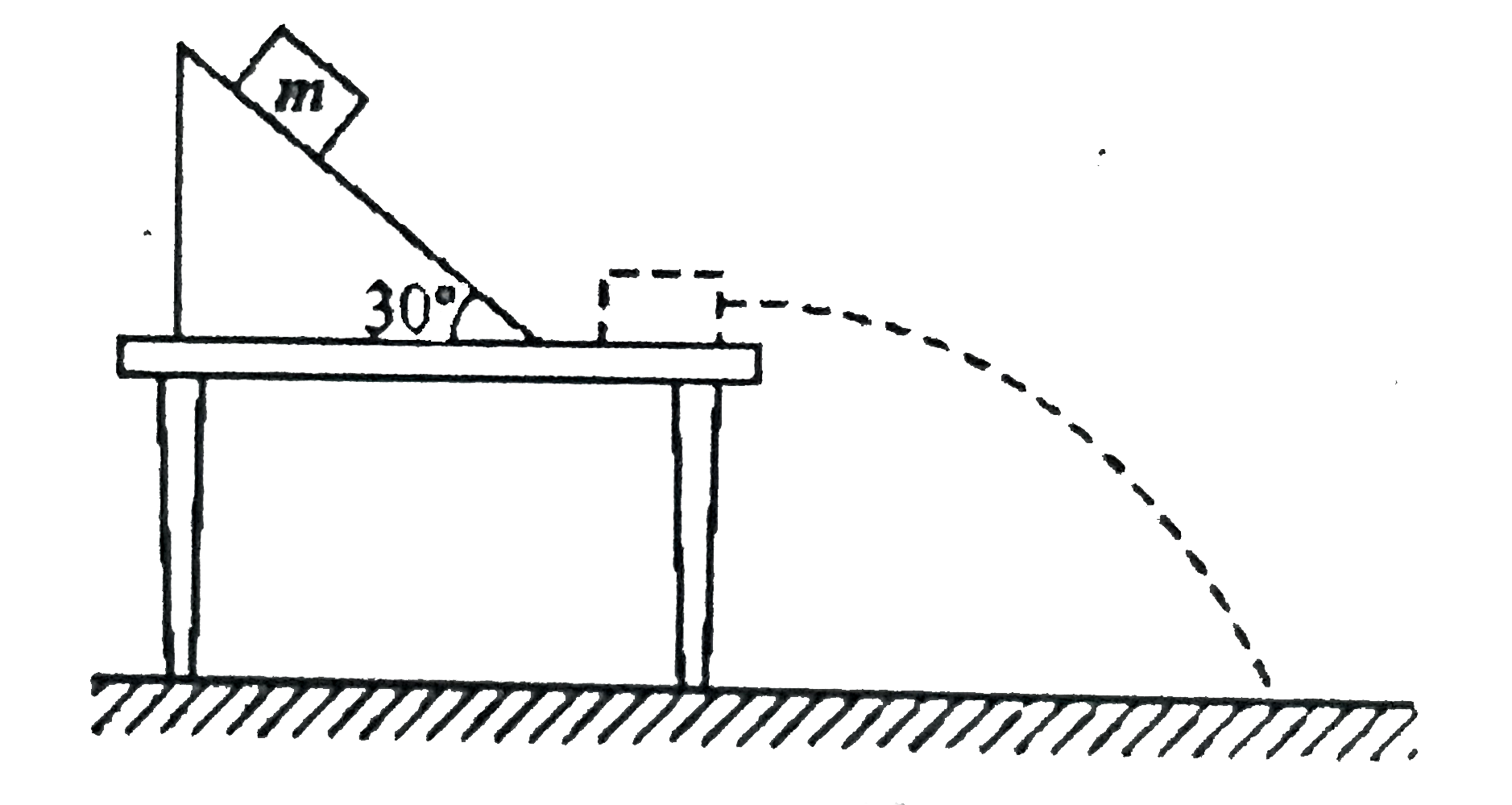
View SolutionA block m= 0.5kg slides down a frictionless inclined plane 2 m long as showi in figure-2.196. It then slides on a rough horizontal table surface of `mu = 0.3` for 0.5 m. It then leaves the top of the table,which is 1.0 m high. How far from the base of the table does the block land ?
View SolutionA baseball is dropped from the roof of at all building. As the ball falls, the air exerts a drag force that varies directly with the speed as f=qv is a constant. Show that the ball acquires a terminal speed. Find the speed of the falling ball as a function of time.
View SolutionA block of metal weighing 2kg is resting on a frictionless plane. It is struck by a jet releasing water at a rate of 1kg/s and at a speed of 5 m/s. Calculate the initial acceleration of the block.
View SolutionHaving gone through a plank of thickness h, a bullet changed its velocity from `v_(0)` to `v_(1)`. Find the time of motion of the bullet on the plank, assuming the resistance force to be proportional to the square of the velocity.
View SolutionA particle of mass M is dropped vertically into a medium that offers resistance proportional to the velocity of the particle. The buoyancy of the medium is negligible, and the resisting force per unit velocity is f. What uniform velocity will the particle finally attain ?
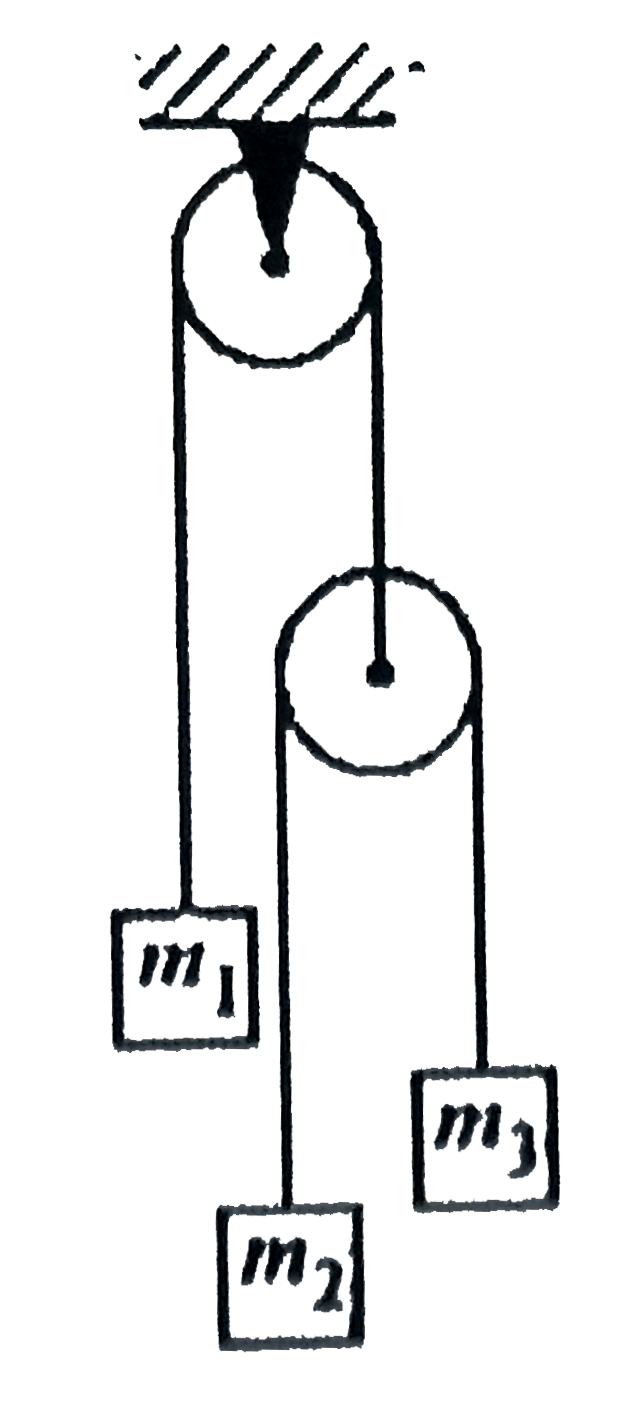
View SolutionConsider the system ofpulleysasshown in figure-2.197. Find the acceleration of the three masses `m^(1),m^(2)` and `m^(3). (m_(1) = I kg,m_(2) = 2kg " and " m_(3) =3kg)`
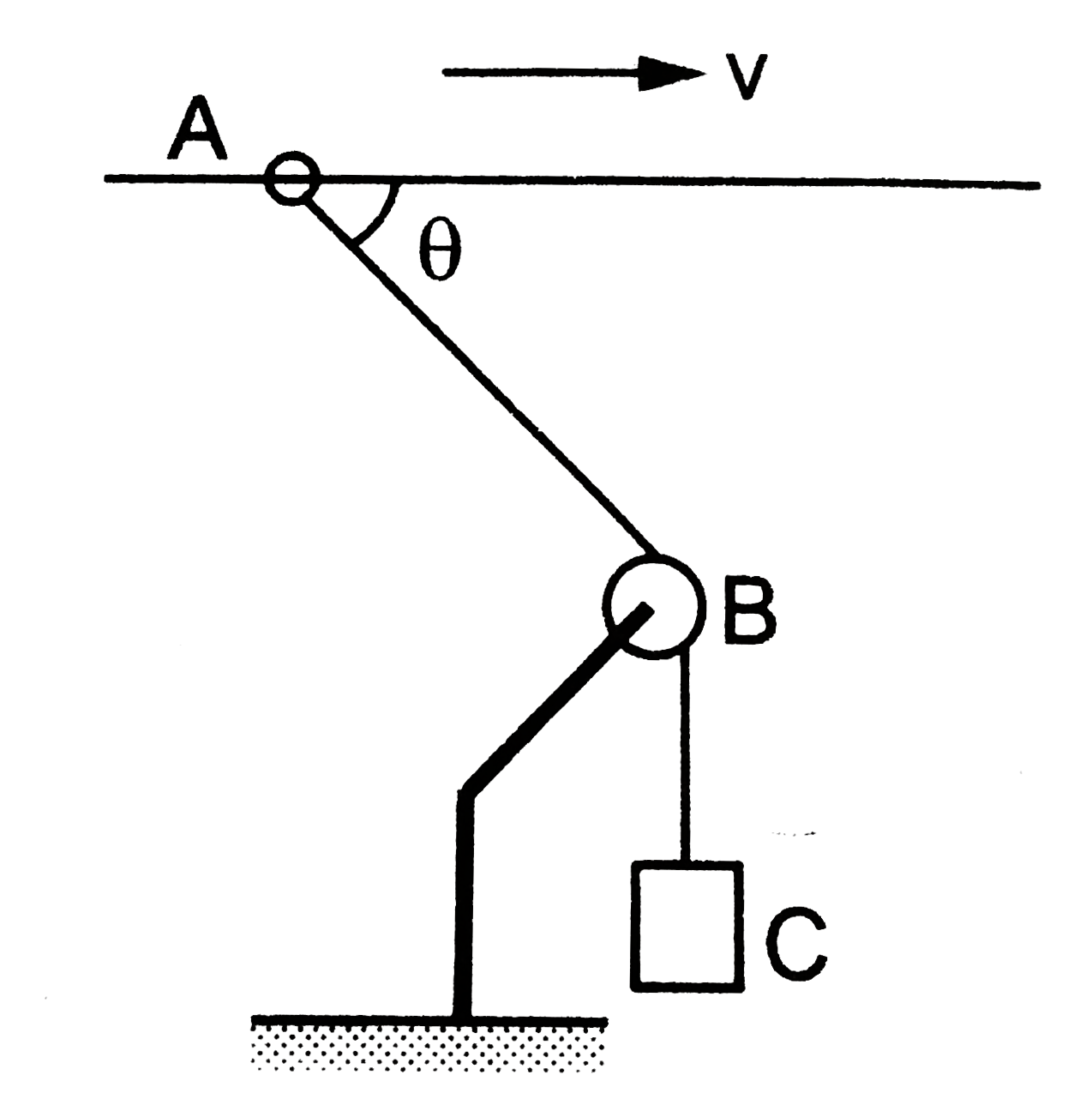
View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of mass `M(=2m)` as shown in figure. At an instant the string between the ring and the pulley makes an angle `theta` with the rod. (a). Show that, if the ring slides with a speed v, the block descends with speed `v cos theta`, (b). With what acceleration will the ring starts moving if the system is released from rest with `theta= 30^0`
View SolutionWhen an archer pulls on the bow string with a force of 500 N, the bow string makes angles of `53^(@)` with the arrow. What is the tension in the string.
View SolutionA man with mass 85 kg stands on a platform with mass 25 kg. He pulls on the free end of a rope that runs over a pulley on the ceiling and has its other end fastened to the platform. The mass of the rope and the mass of the pulley can be neglected, and the pulley is frictionless. With what force does he have to pull so that he and the platform have an upward acceleration of `2.2m/s^(2)`. (Take `g= 10m/s^(2)`)
View SolutionA body of mass `5xx10^(-3)` kg is launched upon a rough inclined plane making an angle of `30^(@)` with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionTwo blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of `0.2kg//m`. The whole system of blocks wires and support have an upward acceleration of `0.2m//s^2`. Acceleration due to gravity is `9.8m//s^2`.
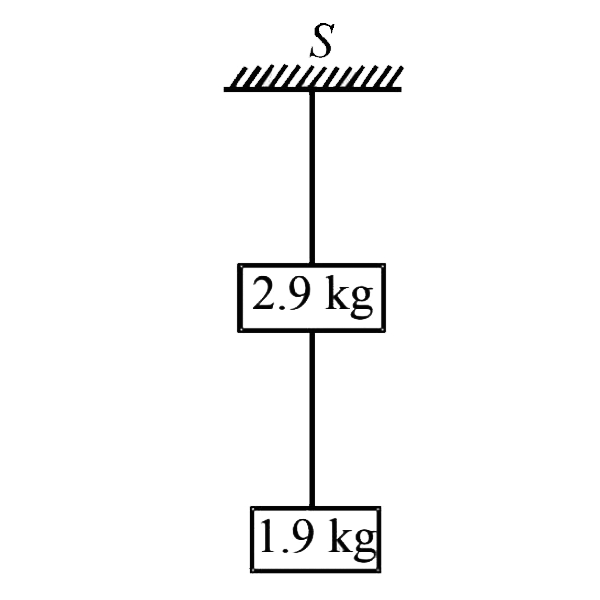
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.
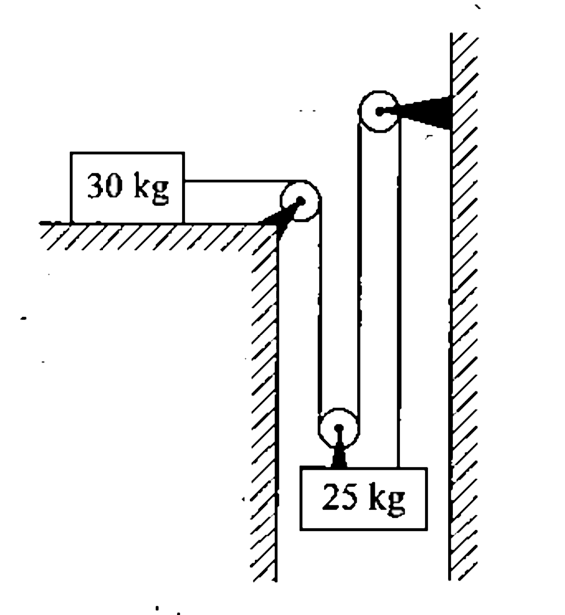
View SolutionThe two blocks shown in figure-2.200 are initially at rest. Assuming ideal pulleys and strings and neglecting friction at all the surfaces, find the accelerations of the two blocks and the tension in the cable.(Take `g = 9.8m/s^(2)`)
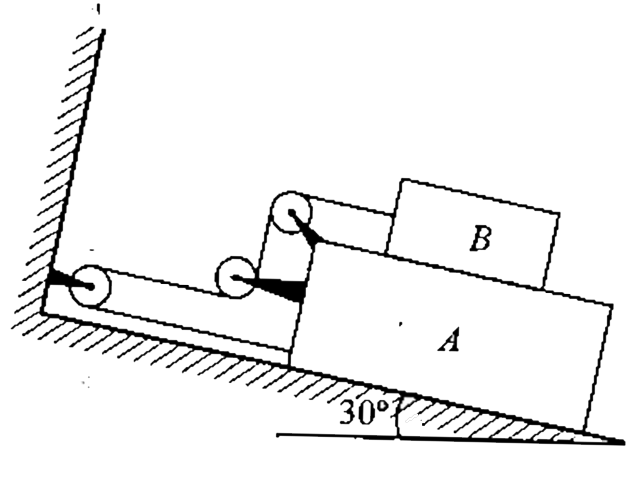
View SolutionIn the figure-2.201 shown the bigger block A has a mass of 40kg and the upper block 5 is of 8kg.The coefficients of friction between all surfaces,of contact are 0.2 (static) and 0.15 (sliding). Find the acceleration of masses when set free.
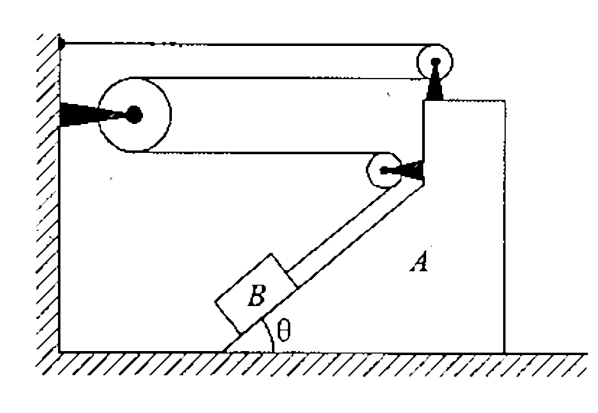
View SolutionFigure-2.202 shows a two block constrained motion system. Block A has a mass M and B has a mass m. If block A is pulled toward right horizontally with an external force F, find the acceleration of the block B relative to ground.

View SolutionSolve the previous problem if the blocks A and B are of different shapes as shown in figure-2.203.
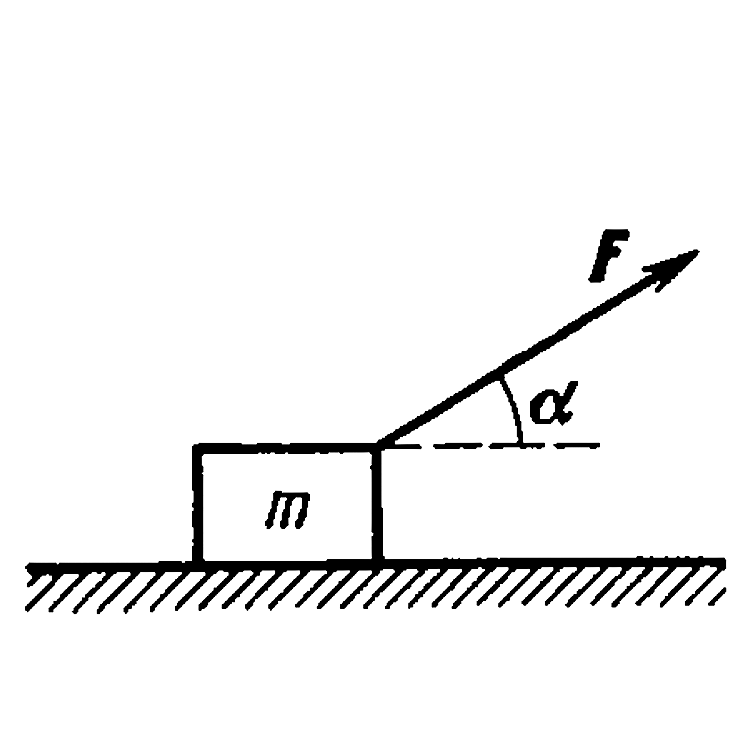
View SolutionAt the moment `t=0` the force `F=at` is applied to a small body of mass `m` resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle `alpha` with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain `llt1/2piR`.
View SolutionIf masses of the blocks A and B shown in figure-2.204 (a) and 2.204(b) are 10kg and 5kg respectively, find the acceleration of the two masses. Assume all pulleys and strings are ideal. (Take `g=9.8m/s^(2)`)
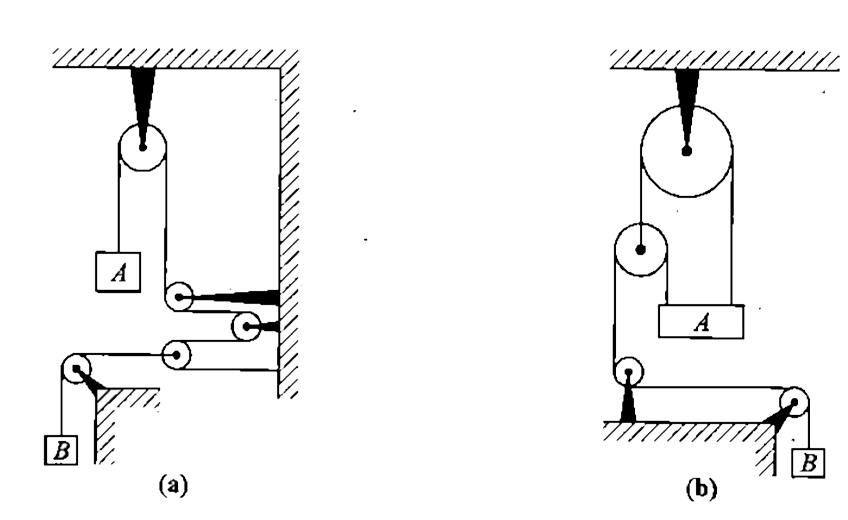
View SolutionIn the figure-2.205 shown in blocks A, B and C has masses `m_(A)= 5 kg, m_(B) = 5 kg` and `m_(C )= 10kg` respectively, find the acceleration of the three blocks. Assume all pulleys and strings are ideal. (Take `g = 10m//s^(2)`)

View SolutionOne end of a string is attached to a 6kg mass on a smooth horizontal table. The string passes over the edge of the table and to its other end is attached a light smooth pulley.Over this pulley passes another string to the ends of which are attached masses of 4kg and 2kg respectively. Show that the 6kg mass moves with an acceleration of `8g//17`.
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` kept touching each other on an inclined plane of inclination a with the horizontal. Show that (i) theforce of interaction between the blocks is `((mu_(1)-mu_(2))m_(1)m_(2)gcosalpha)/((m_(1)+m_(2)))` and (ii) the minimum value of `alpha` at which the blocks just start sliding is `a = tan^(-1).(mu_(1)m_(1)+mu_(2)m_(2))/(m_(1)+m_(2))` . Where `mu_(1)` and `mu_(2)` are the coefficients of friction between the block `m_(1)` and the inclined plane and between the block `m_(2)` and the inclinedplane respectively.
View SolutionTwo block `A` and `B` of masses `1kg` and`2kg` respectively are connected by a string, passing over a light frictionless pulley as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment `t = 0`, a force `F = 20 t` starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of `A` when `B` loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =`g =10 m//s^(2))`
View SolutionA worker wishes to pile a cone of sand onto a circular area in his yard. The radius of the circle is r,and no sand is to spill on to the surrounding area. If `mu` is the static coefficient of friction between each layer of sand along the slope and the sand, show that the greatest volume of sand that can be stored in this manner is `(1)/(3) pi muR^(3)`.
View SolutionA `30 kg` mass is initially at rest on floor of a truck . The coefficient of static friction between the mass and the floor of truck in `0.3` and coefficient of kinetic friction is `0.2` . Initially the truck is travelling due east at constant speed.Find the magnitude and direction of the friction force acting on the mass , if : (take `g = 10 m//s^(2))`
(a) the truck acceleration at `1.8 m//s^(2)` eastward
(b) the truck acceleration at `3.8 m//s^(2)` westward
View SolutionAt the moment t = 0 a stationary particle of mass m experiences a time-dependent force `F = kt(t'-t)`,where is a constant vector, t' is the time during which the given force acts. Find :
(a) The momentum of the particle when the action of the force discontinued,
(b) The distance covered by particle while the force acted.
View SolutionAn empty tin can of mass M is sliding with speed `V_(0)` across a horizontal sheet of ice in a rain storm. The area of opening of the can is A. The rain is falling vertically at a rate of n drops per second per square metre. Each rain drop has a mass m and is falling with a terminal velocity `V^(n)`. (a) Neglecting friction, calculate the speed of the can as a function of time,(b) Calculate the normal force ofreaction ofice on the can as a function of time.
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle `theta` with the horizontal. The coefficient of kinetic friction between the crate and the surface is `mu`. Find the angle `theta` such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View SolutionA small body was launched up an inclined plane set at an angle `alpha=15^@` against the horizontal. Find the coefficient of friction, if the time of the ascent of the body is `eta=2.0` times less than the time of its descent.
View SolutionA motor-boat of mass m moves along a lake with velocity `v_(0)`. At the moment t = 0 the engine of the boat is shut down. Assuming the resistance of the particle to-be proportional to the velocity of the boat F = - rv, find:
(a) How long the motor boat moved with the shut down engine,
(b) (b) The velocity of the motor boat as a function of the distance covered with the shutdown engine, as well as total distance covered till the complete stop.
(c ) The mean velocity of the motor boat over the time interval (beginning with the moment t=0), during which its velocity decreases `eta` times.
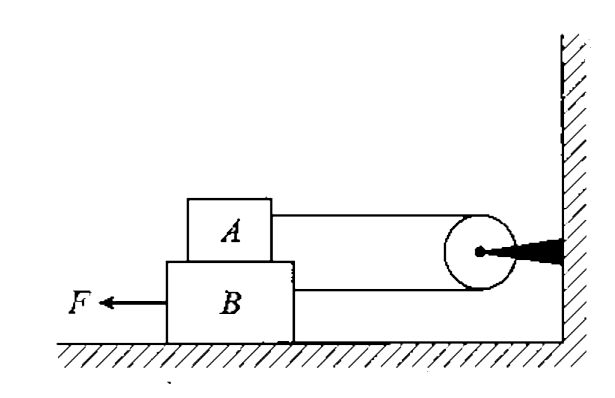
View SolutionBlock A in figure-2.207 weights 2.7N and block B weighs 5.4 N the coefficient of kinetic friction between all surfaces is 0.25. Find the magnitude of the horizontal force F necessary to drag blocks to the left at constant speed if A and B are connected by a light, flexible cord passing around a fixed frictionless pulley
View SolutionA uniform cone of half angle `phi` stands on a rough inclined plane. Show that as the inclination of the plane is increased the cone will slide down before it topples over if the coefficient of friction is less than 4 tan `phi`.
View SolutionA weight of 200kg hangs freely from the end of a rope. The weight is hauled up vertically from rest by winding up the rope. The pull starts at 250 kg and diminishes uniformly at the rate of one kg per metre wound up. Find the velocity after 30 metres have been wound up. Neglect the weight ofthe rope.
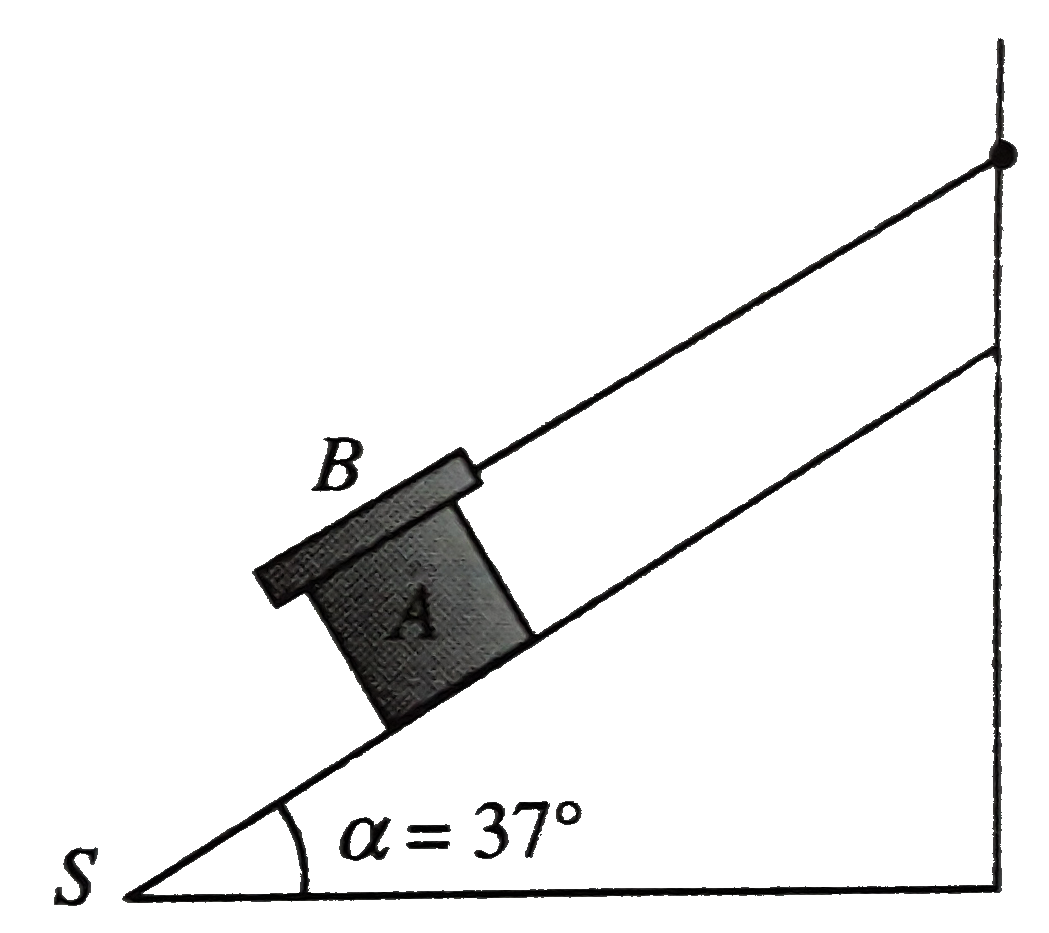
View SolutionA block A of weight `W` slide down an inclined plane S of slope`37^(@)`at a contact velocity,while the plane B also of weight `W` rests on top of `A` The plank B is atteched by a cord to the top of plane .The coefficient of kinetic friction`mu` is the same between the surface A and B and between S and A Determine the value of `1//mu`
View SolutionA small disc A is placed on an inclined plane forming an angle `alpha` with the horizontal and is imparted an initial velocity `v_(0)`. Find how the velocity of the disc depends on the angle `theta`, shown in figure-2.209, if the friction coefficient `mu = tan alpha` and at the initial moment `theta=pi//2`

View SolutionA horizontal plane with the coefficient of friction `k` supports two bodies: a bar and an electric motor with a battery on a block. A thread attached to the bar is wound on the shaft of the electric motor. The distance between the bar and the electric motor is equal to `l`. When the motor is switched on, the bar, whose mass is twice as great as that of the other body, starts moving with a constant acceleration `w`. How soon will the bodies collide?
View SolutionA fixed pulley carries a weightless thread with masses `m_(1)` and `m_(2)` at its ends. There is friction between the thread and the pulley. It is such that the thread starts slipping when the ratio `m_(2)//m_(1)=eta_(0)` find :
(a) The friction coefficient
(b) The acceleration of the mass when `m_(2)//m_(1)=eta gt eta_(0)`
View SolutionA body with zero initial velocity slips from the top of an inclined plane forming an angle `alpha` with the horizontal. The coefficient of friction `mu` between the body and the plane increases with the distance s from the top according to the law `mu = bs`. After what distance the body will stop.
View SolutionA homogeneous chain of length 2l and mass M lies on an absolutely smooth table. A small part of the chain hangs from the table. At the initial moment, the part of the chain lying on the table is held and released, after which the chain begins to slide off the table under the weight of the hanging end. Find the velocity of the chain when the length of the hanging part is equal to `x(x lt I)`. Also calculate the acceleration and the force with which it acts on the edge of the table.
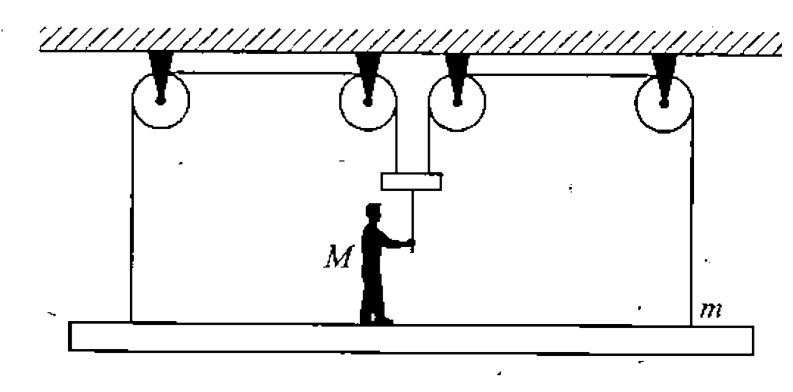
View SolutionA boy of mass M stands on a platform of mass m as shown in figure-2.210, supporting two stringsvia a massless support S. Strings are passing over the pulleys and other ends are connected to the platform as shown. Find the acceleration of the platform and the boy if he applies a constant force T to the string he isholding, which is connected to support S.
View SolutionAn empty box is put on the pan of a spring balance and scale is adjusted to zero.A stream of small identical beads,each of mass 4.5gm are then dropped into the box from height 7.6m at constant rate of 100 beads/sec. If the collision between each bead and box is completely inelastic fmd the reading of the scale, 10 seconds after beads begin to hit the box. '
View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
View SolutionA 12kg monkey climbs a light rope.The rope passes over a pulley and is attached to a 16kg bunch of bananas resting on floor. Mass and friction in the pulley are negligible so that the pulley's only effect is to reverse the direction of the rope. What is the maximum acceleration the monkey can have without lifting the bananas ? (Take `g=10m//s^(2)`)
View SolutionA heavy mass M resting on the ground is attached to a small mass m via massless inextensible string passing over a pulley.The string connected to M is loose.The smaller mass falls freely through a height h and the string becomes tight. Obtain the time from this instant when the heavier mass again makes contact with the ground. Also obtain the loss in K.E. when M is jerked in to motion.
View SolutionA bar of mass m is pulled by means of a thread up an inclined plane forming an angle `theta` with the horizontal as shown in figure-2.211. The coefficient of friction is `mu`. Prove that
(a)`alpha=tan^(-1)mu`, where `alpha` is the angle which the thread must from with the inclined plane for the tension of the thread to be minimum.
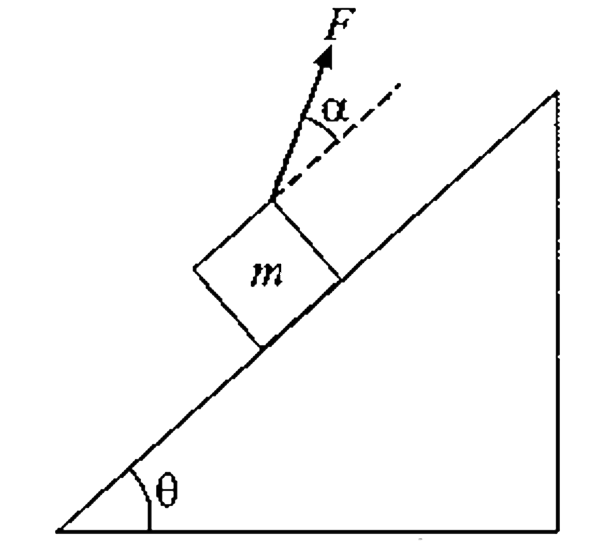
View SolutionFind the mass M in the situation shown in figure-2.212 such that m remains at rest on the front surface of `M_(1)`. The coefficient of friction between the front surface of `M_(1)` and that of m is `mu`.

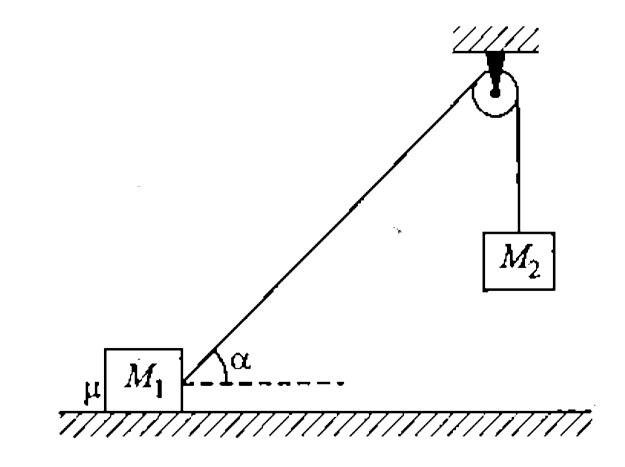
View SolutionA block of mass `m_(1)` rests on a rough horizontal plane with which its coefficient of friction is `mu`. A light string attached to this block passes over a light frictionless pulley and carries another block of mass `m_(2)` as shown in figure-2.213. When the system is just about to move, find the value of `mu` in terms of `m_(1) m_(2)` and `alpha`. Also find the tension in the string.
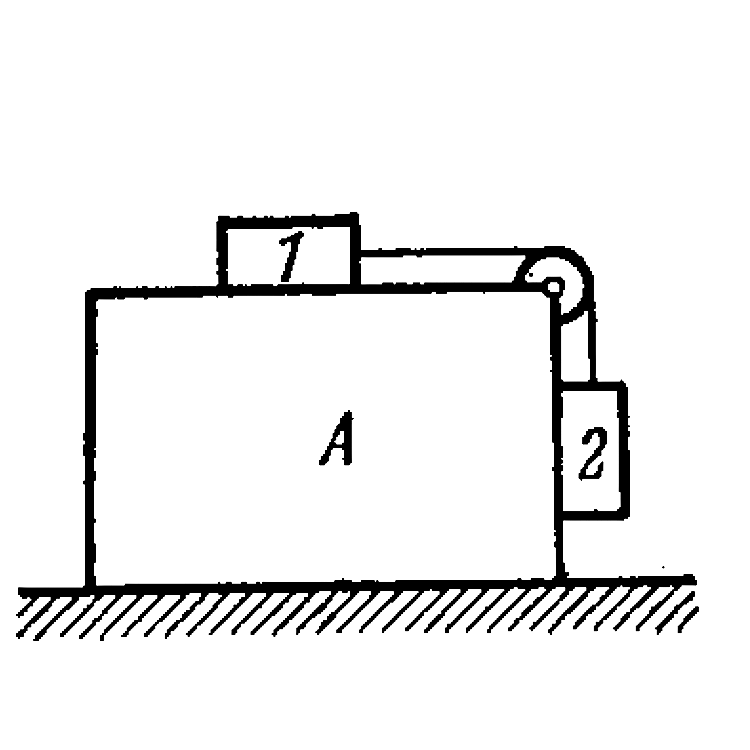
View SolutionWhat is the minimum acceleration with which bar A (figure) should be shifted horizontally to keep bodies 1 and 2 stationary relative to the bar? The masses of the bodies are equal, and the coefficient of friction between the bar and the bodies is equal to k. The masses of the pulley and the threads are negligible, the friction in the pulley is absent.
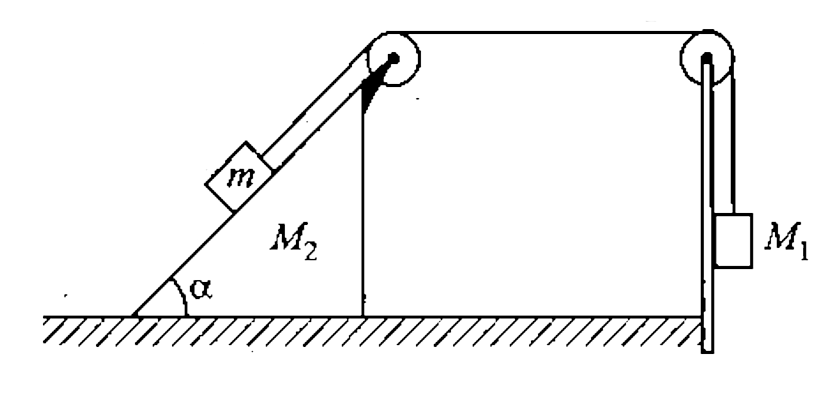
View SolutionFind out the value(s) of `theta` of the inclined plane such that the mass m remains at rest on the wedge of mass `M_(2)` as shown in figure-2.215. Friction between the small block and the wedge plane is `mu` and all other surface are smooth.
View SolutionIn the figure-2.216, the masses A and B are of 4kg and 12 kg respectively. When the system is released from rest, find the time after which the block B will hit the ground.
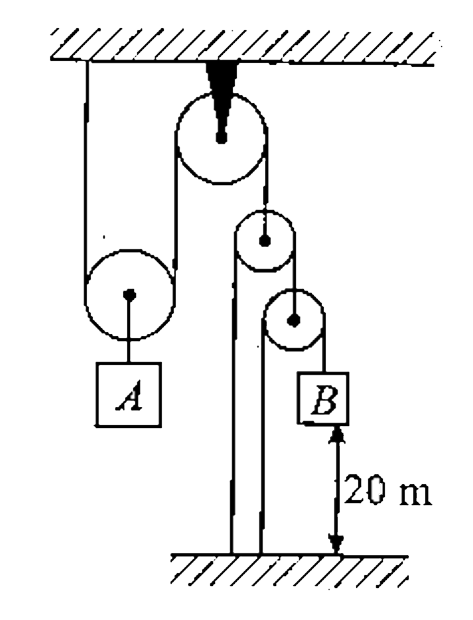
View SolutionIn the figure2.217 all the surfaces are frictionless. What force F is required to be applied on the bigger block so that `m_(2)` and `m_(3)` will remain at rest on it.
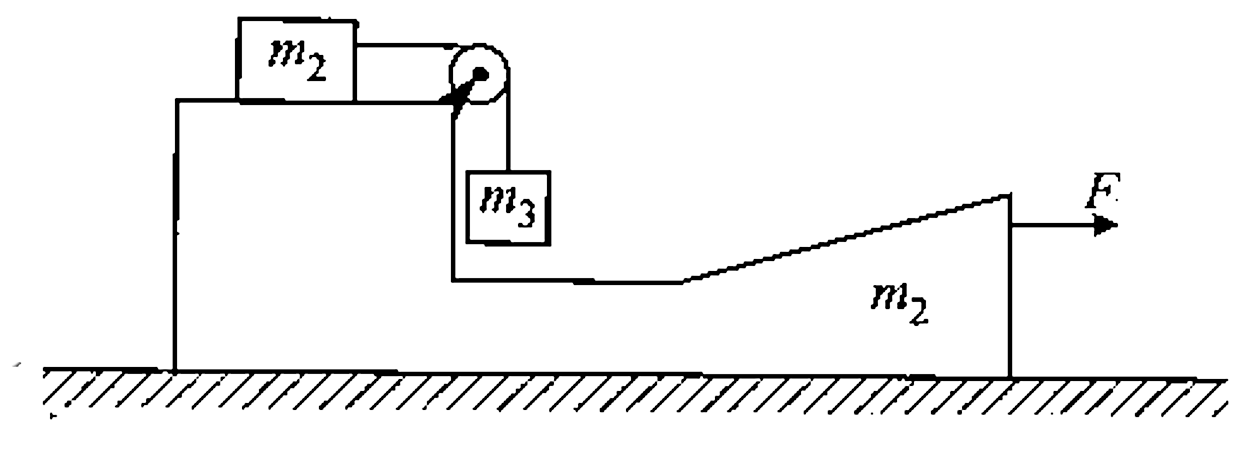
View SolutionMass of block B shown in figure-2.218 is m and that of cart C is M. Show that the maximum value of force F such that the block does not slip over the surface of C, has a magnitude
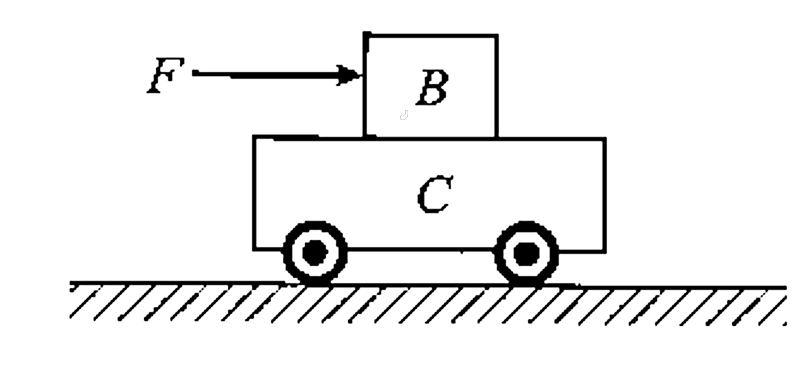
View SolutionIn the figure-2.219 shown, if the system is in equilibrium. Find the relation in `m_(1)` and `m_(2)` forthe case (i) if the bar is just going to slide and (ii) if box is just going to slide.
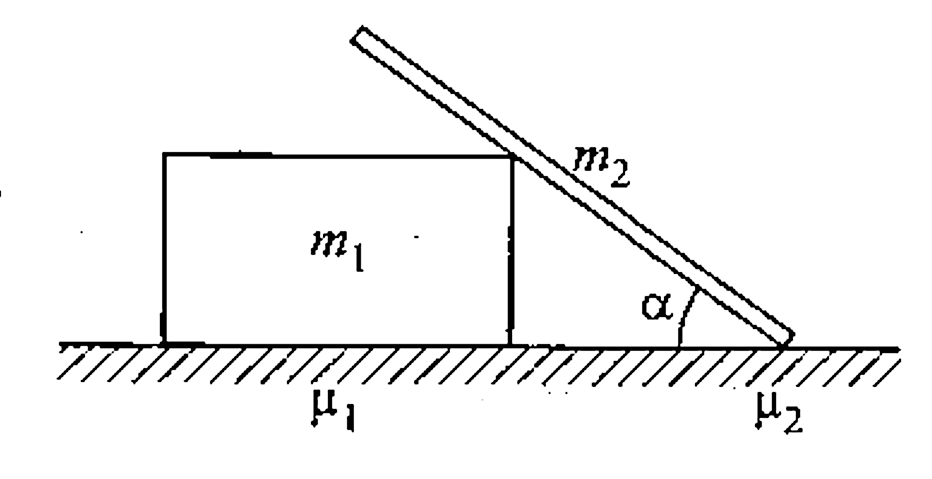
View SolutionA meter stick is hung from two spring balances A and B of equal lengths that are located at the 20 cm and 70 cm marks of the meter stick. Weights of 2.0N are placed at the 10cm and 40cm marks, while a weight of 1.0N is placed at the 90cm mark. The weight of the uniform meter stick is 1.5 N. Determine the scale readings of the two balances A and B.
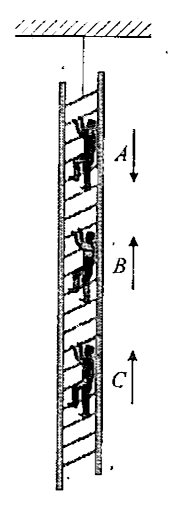
View SolutionA ladder is hanging from ceiling as shown in figure-2.220. Three men of masses 10kg,12kg and 8kg are climbing in such away that man A is going down with an acceleration of `1.6 m//s^(2)` and C is rising up with an acceleration of `0.9 m//s^(2)` and man B is going up with a constant speed of `0.6m//s`.. Find the tension in the string supporting the ladder.
View SolutionA 54kg girl on ice skates on a frozen lake pulls with a constant force on all light rope that is tied to a 41 kg sled. The sled is initially 22m from the girl, and both the sled and the girl start from rest. Neglecting friction, determine the distance the girl travels to the point where she meets the sled.
View SolutionThe force which keeps a hot air balloon is the buoyant force F. Suppose a hot air balloon ofmass M has a downward acceleration of magnitude a.Find the ballast mass that must be dropped from it to cause the balloon to accelerate upward with same magnitude a.'
View SolutionA 20 kg bucket is lowered by a rope with constant velocity of 0.5m/s. What is the tension in the rope? A 20kg bucket is lowered with a constant downward acceleration of `1m//s^(2)`. What is the tension in the rope? A 10kg bucket is raised with a constant upward acceleration with same magnitude a.
View SolutionA heavy chain with a mass per unit length `p` is pulled by the constant force `F` along a horizontal surface consisting of a smooth section and a rough section. The chain is initially at rest on the rough surface with `x = 0` . If the coefficient of kinetic friction between the chain and the rough surface is `mu_(k)` determine the velocity `v` of the chain when `x = L` . The force `F` is greater than `mu_(k) pgL` in under to initiate the motion ,

View SolutionA 400 kg ice boat moves on runners on essentially frictionless ice.A steady wind blows,applying a constant force to the sail. At the end of 8.0 sec run,the acceleration is `0.5m/s^(2)`. (a) What was the acceleration at the beginning of the run? (b) What was the force due to the wind ? (c) What retarding force must be applied at the end of 4.0 sec to bring the ice boat to rest by the end of the next 4 sec ? (assume boat was at rest at time t = 0)
View SolutionA box is placed in the middle of the bed of a flatbed truck and is not strapped down. The coefficient `mu` between the bed and the box is 0.75. If the truck is travelling at a speed of 22m/s along a horizontal street, what is the minimum stopping distance such that the box will not slide ?
View SolutionA person weighting 400N stands on spring scales in an elevator that is moving downward with constant speed of 4m/s the brakes suddenly grab, bringing the elevator to a stop in 1.8 s. Describe the scale readings from just before the brakes grab until after the elevator is at rest.
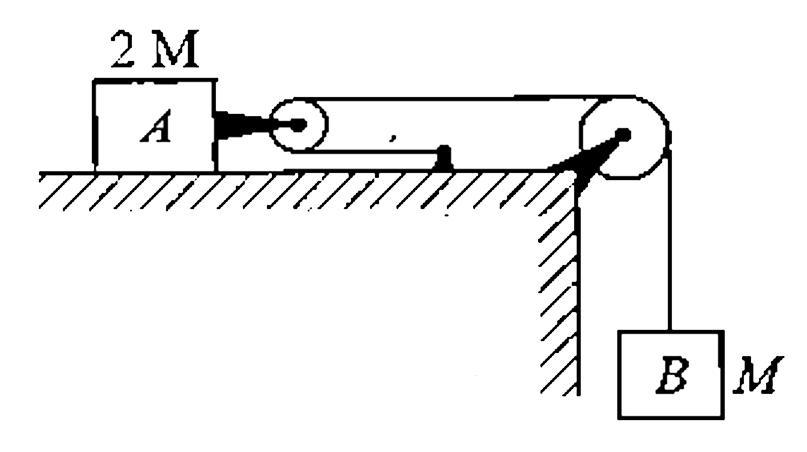
View SolutionDetermine the expression for the acceleration of blocks and B as shown in figure-2.222. Assume that the surface of body A are small and have well lubricated bearings. Also find the force, the pulley exerts on the clamp ?
View SolutionThe upper portion of an inclined plane of inclination `alpha` is smooth and the lower portion is rough. A particle slides down from rest from the top and just comesto rest at the foot.If the ratio ofthe smooth length to rough length is w : find the coefficient of friction.
View SolutionA light container filled with apples is to bed ragged on a rough floor where sliding friction coefficient is 0.35. The rope used for the purpose can bear a maximum of 1100 N tension. Find the angle with the horizontally which one has to pull the rope to carry maximum amount of apples. Also find this maximum amount of apples in kilograms.
View SolutionA simple At wood machine composed of a single pulley and two masses `m_(1)` and `m_(2)` is on an elevator. When `m_(1)`=44.7 kg and `m^(2)`=45.3 kg, it takes 5.0 sec for mass `m_(2)` to descend exactly one meter from rest relative to the elevator. What is the elevator's motion?
View SolutionWhen travelling freely a train is subjected to resistances which vary directly as the velocity and at 9= kph this is equal to 1 percent of the weight of the train. The brakes when applied create a further resistance equal to `l//16th` of the weight of the train. If the brakes are suddenly applied when the velocity is 90kph find the time and distance travelled before the train comes to rest.
View SolutionA bar of mass m resting on a smooth horizontal plane starts moving due to the force `F=mg//3` of constant magnitude. In the process of its rectilinear motion the angle `alpha` between the direction of this force and the horizontal varies as `alpha=as`, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle `alpha`.
View SolutionA 20kg box rests on the flat floor of a truck. The coefficients of friction between box and floor are `mu_(s)`= 0.15 and `mu_(k)`=0.10. The truck stops at a stop sign and then starts to move with an acceleration of `2 m/s^(2)`. If the box is 2.2 m from the rear of the truck when the truck starts, how much time elapses before the box falls of fthe rear of the truck? How far does the truck travel in this time.
View SolutionIf the coefficient of static friction between a table and a uniform massive rope is `mu`, what fraction of the rope can hang over the edge of a table without the rope sliding.
View SolutionTwo small balls of the same size and of mass `m_(1)` and `m_(2)(m_(1) gt m_(2))` are tied by a thin light thread and dropped from a large height. Determine the tension `T` of the thread during the flight after the motion of the balls has become steady. (Air resistance force is same on two balls)
[Take `m_(1)=2kg`, `m_(2)=1kg`, `g=10m//s^(2)`]
View SolutionA small block of mass `m` is projected on a larger block of mass `10 m` and length `l` with a velocity `v` as shown in the figure. The coefficient of friction between the two block is `mu_(2)` while that between the lower block and the ground is `mu_(1)`. Given that `mu_(2) gt 11 mu_(1)`.

(a) Find the minimum value of `v`, such that the mass `m` falls off the block of mass `10 m` .
(b) If `v` has minimum value, find the time taken by block `m` to do so.
View SolutionA block with mass `m_(1)` is placed on an inclined plane with slope angle `alpha` and is connected to a second hunging block with mass `m_(2)` by a cord passing over a small . Friction less pulley as shown in fig 7.247 . The coefficient of static friction is `mu_(2)` and the coefficient of kinetic friction is `mu_(s)`

a. Find the mass `m_(2)` for which block `m_(1)` moves up plane at constant speed once it is set in motion
b. Find the mass `m_(2)` for which block `m_(1)` moves down the plane at constant speed once it is set in motion
c.For what range of `m_(2)` will the blocks remain at rest if they are released from rest?
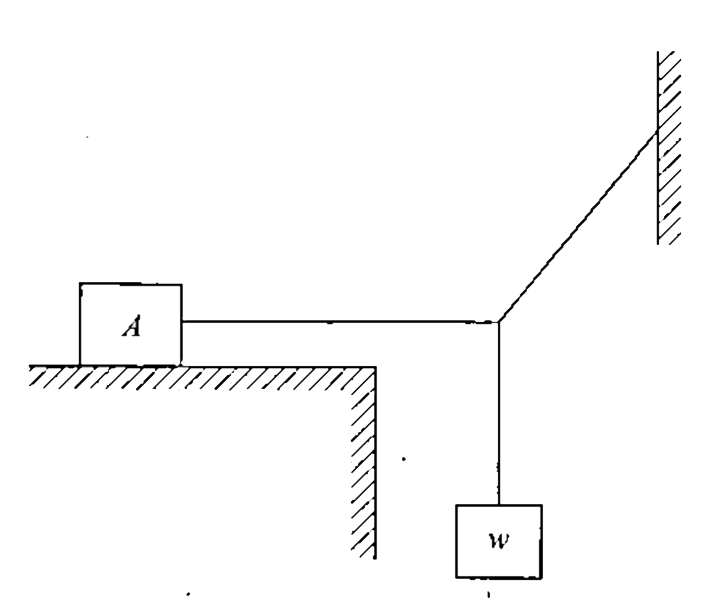
View SolutionBlock A in figure weights 90 N. The coefficient of static friction between the block and the surface on which it rests is 0.3. The weight w is 15N, and the system is in equilibrium. Find the friction force exerted on block A.(b) Find the maximum weight w for which the system will remain in equilibrium.
View SolutionA uniform rod of length `L` rests against a smooth roller as shown in Fig. Find the friction coefficient between the ground and the lower end if the minimum angle that the rod can make with the horizontal is `theta`.

View SolutionBlock `A` of mass `m` and block `B` of mass `2m` are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at `45^(@)` to the horizontal on both sides . The coefficient of friction between the block `A`and the wedge is `2//3` and that between the block `B` and the wedge is `1//3` .If the system of `A and B` is released from rest then find .
a. the acceleration of `A`
b. tension in the string
c.the magnitude and direction of the frictional force acting on `A`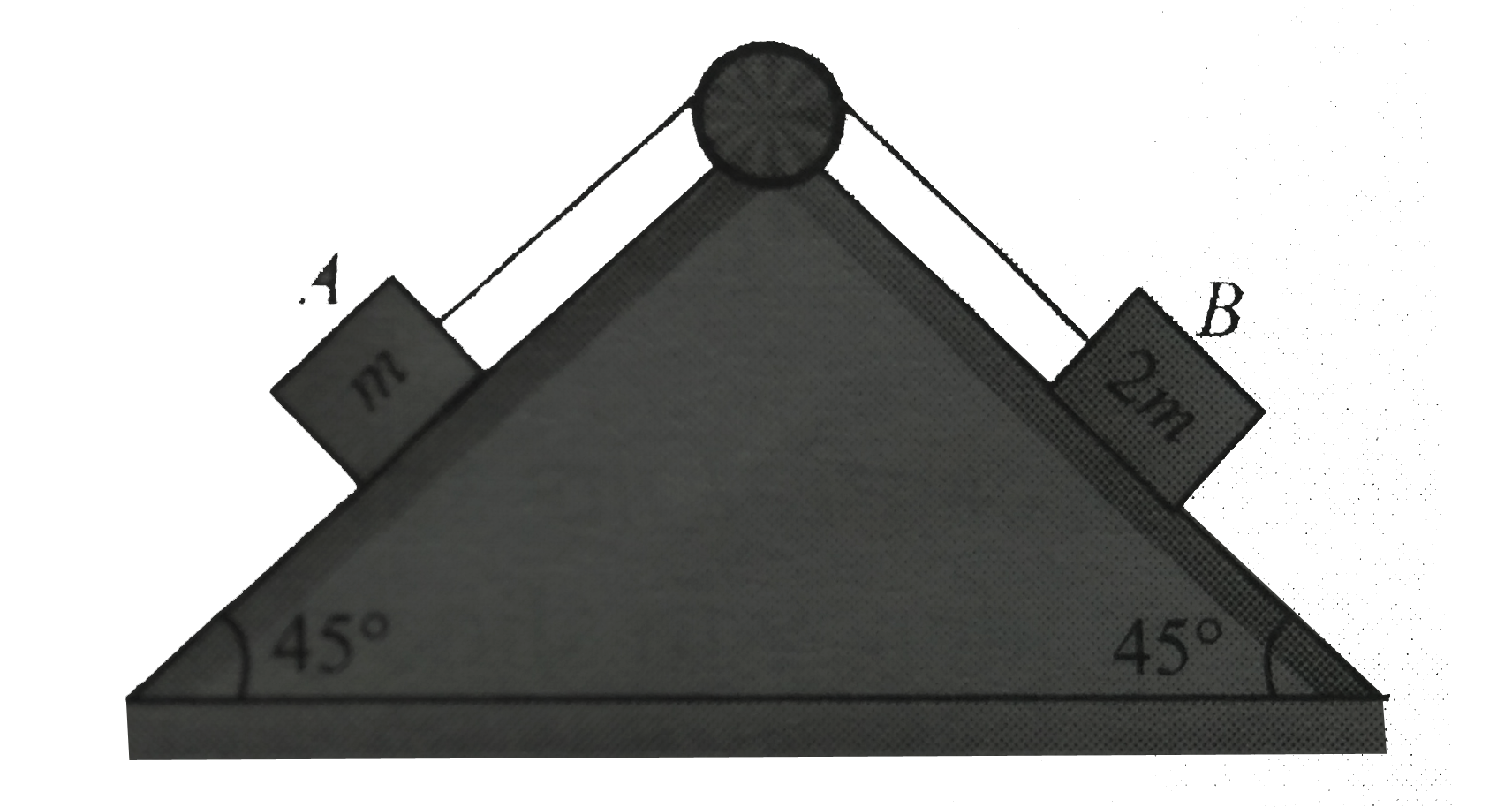
View SolutionFind the acceleration of the prism of mass M and that of the bar of mass m shown in figure.
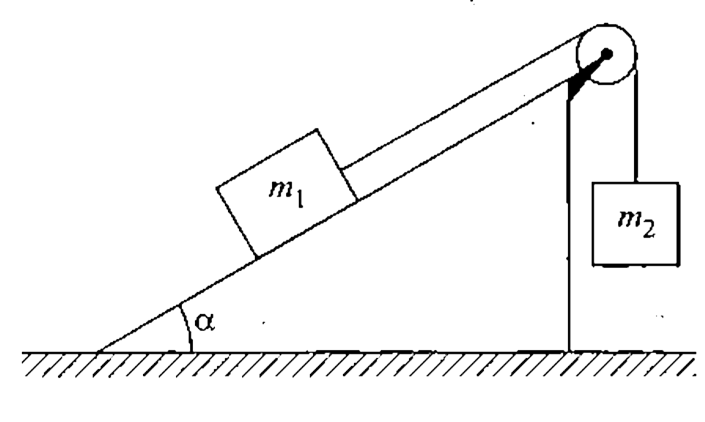
View Solution(i) A uniform ladder of length L and weight w rests against a vertical wall and makes an angle `theta` with the horizontal ground. If the coefficient of friction at the point of contact of the ladder with the wall and ground is `mu`, show that the greatest height x, measured along the ladder from the foot to which a man of weight w may climb without the ladder slipping is given by
`(x)/(L) = (mu(W+w))/(W(1+mu^(2))) (mu +tan theta) - (w)/(2W)`
(ii) If the wall be smooth and coefficient of friction between ladder and ground be 0.25, show that
`x = (L)/(4) (1-(w)/(W)) tan theta - (wL)/(2W)`
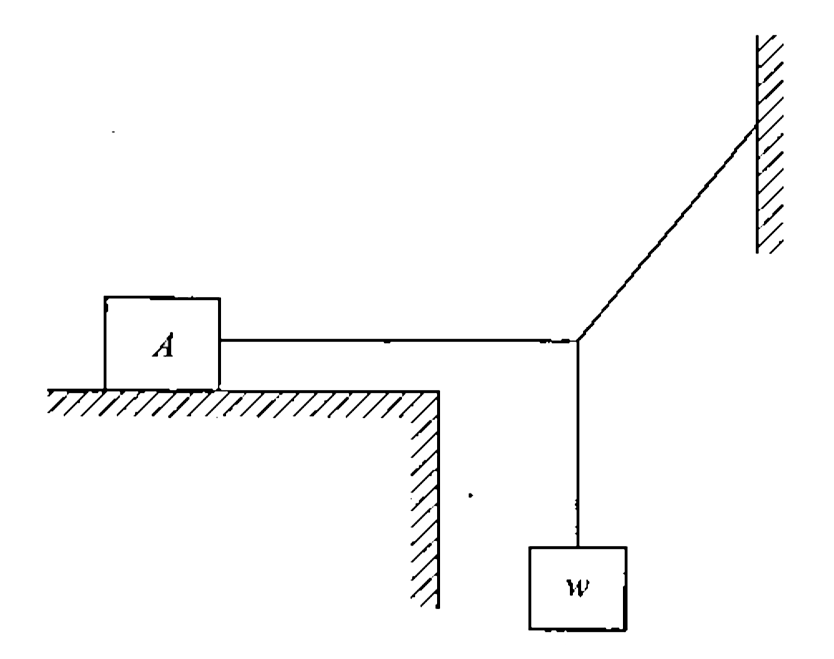
View SolutionConsider the situation shown in figure. Find the acceleration of the system and the tension in the strings.
View SolutionTwo masses `M_(1)` and `M_(2)` are connected by light string, which passes over the top of a smooth plane inclined at `30^(@)` to the horizontal, so that one mass rests on the plane and the other hangs vertically as shown in figure. It is found that `M_(1)`, hanging vertically can draw `M_(2)` up the full length of the plane in half the time in which `M_(2)` hanging vertically draws `M_(1)` up. Find `M_(1)//M_(2)`. Assume pulley to be smooth. Initially at time `t = 0` smooth masses `M_(1) = 15 kg` and `M_(2) = 10 kg` are held at rest and then they released. if after one second. the string snaps, find the further time taken for the 15 kg mass to return to its original position on the plane. Take `g = 10 m//s^(2)`

View SolutionTwo block , with masses `m_(1)` and `m_(2)` are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude `F` is applied to the top block at an angle `alpha` below the horizontal . The coefficient of friction between `m_(1)` and `m_(2)` are `mu_(s)`
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together

View Solution
Unsolved Numerical Problem questions and complete solutions for chapter NEWTONS LAWS OF MOTION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11