Complete Solutions to Particle Exercise of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| PHYSICS GALAXY | Particle Exercise |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionFor particles of equal masses M that move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionMass `M` is split into two parts `m` and `(M-m)`, which are then separated by a certain distance. What is the ratio of `(m//M)` which maximises the gravitational force between the parts ?
View SolutionIn a double star, two stars (one of mass `m` and the other of mass `2m`) distance `d` apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.
View SolutionTwo concentric spherical shells have masses `m_(1)`, `m_(2)` and radii `R_(1)`,`R_(2) (R_(1) lt R_(2))`. Calculate the force by this system on a particle of mass `m`, if it is placed at a distance `((R_(1) + R_(2)))/(2)` from the centre.
View SolutionThe distance between the centres of the Moon and the earth is `D`. The mass of the earth is `81` times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure`-6.30`. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) `r lt x lt 2r, (b) 2rlt x lt 2R "and"(c) xgt2R`.
View SolutionThe gravitational field in a region is given by `(2hati+2hatj)`N/kg. What is the work done by an external agent in slowly shifting a particle of mass 10 kg from origin to point (5,4).
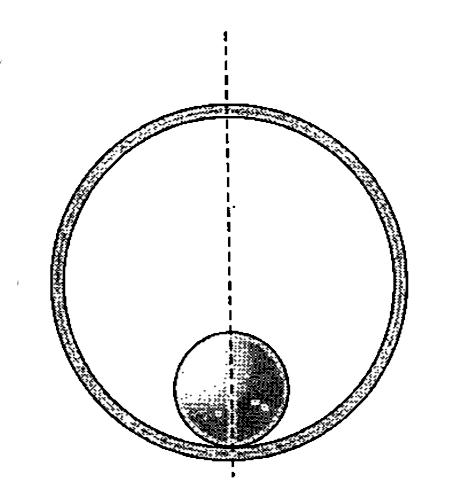
View SolutionInside a uniform sphere of density `rho` there is a spherical cavity whose centre is at a distance `l` from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View SolutionA small point mass m is placed at the centre of curvature of acircular are of radius R and mass 3 m as shown in figure`-6.31.`Find the net gravitational force acting on the point mass.

View SolutionA small point mass m is to be thrown with such a speed at a distance x from the axis of a long cylinder of radius R and density `rho`, so that m starts revolving around the cylinder in a circular orbit of radius x with centre on the axis of cylinder. Find the speed with which point mass is thrown.
View SolutionFigure shows two uniform rods of mass M and length l placed on two perpendicular lines. A small point mass m is placed on the point of intersection of the two lines. Find the net gravitational force experienced by m.

View SolutionWhat will be acceleration due to gravity on the surface of the moon if its radius were `(1//4)^(th)` the radius of earth and its mass `(1//80)^(th)` the mass of earth? What will be the escape velocity on the surface of moon if it is `11.2 km//s` on the surface of the earth? (given that `g=9.8 m//s^(2)`)
View SolutionThe diameter of a planet is four times that of the earth. Find the time period of a pendulum on the planet, if it is a second pendulum on the earth. Take the mean density of the planet equal to that of the earth,
View SolutionImagine a new planet having the same density as that of earth but `3` times bigger than the earth in size. If the acceleration due to gravity on the surface of earth is `g` and that on the new plane is `g` , then :
View SolutionWeight fo a body of a mass m decreases by 1% when it is raised to height h above the earth's surface. If the body is taken to depth h in a mine, change in its weight is
View SolutionA tunnel is dug along a chord of the earth. a perpendicular distance `R/2` from the earth\'s centre is dropped. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionFind the height over the earth\'s surface at which the weight of a body becomes half of its value at the surface.
View SolutionA body is weighted by a spring balance to be 1.000 kg at the north pole. How much will it weight at the equator. Account for the earth\'s rotation only.
View SolutionA body suspended on a spring balance in a ship weighs `W_(0)` when the ship is at rest. When the ship begins to move along the equator with a speed `v`, show that the scale reading is very close to `W_(0) (1+-2omegaV//g`), where `omega` is the angular speed of the earth.
View SolutionThe kinetic energy needed to project a body of mass m from the eath surface (radus R) to infinity is
View SolutionHow much work is done in circulating a small object of mass m around a sphere of mass m in a circle of radius R.
View SolutionDistance between the centres of two stars is `10alpha.` The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionTwo particle each of mass M are fixed at positions (0, a) and `(0, -a)`. Another particle of mass `M//2` is thrown from origin along + z axis so that it is just able to reach a point `(0, 0, 2sqrt(3)a)`. Find the soeed with which it was projrcted.
View SolutionThe gravitational field in a region is given by `E = (2 hati + 3 hatj) N//kg`.
Find the work done by the gravitational field when a particle of mass `1 kg` is moved on the line `3y+ 2x = 5` from `(1 m,1m)` to `(-2 m, 3m)`.
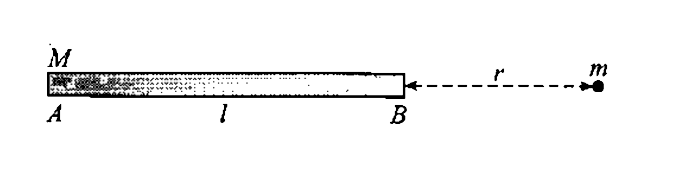
View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
View SolutionTwo satellites `A` and `B` of the same mass are orbiting the earth at altitudes `R` and `3R` respectively, where `R` is the radius of the earth. Taking their orbit to be circular obtain the ratios of their kinetic and potential energies.
View SolutionAs satellite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth\'s surface. Find a). its speed in the orbit b). its kinetic energy. c). The potential energy of the earth satelilte system and d). its time period. Mass of the earth `=6xx10^24kg`.
View SolutionA satellite is to revolve around the earth in a circle of radius 8000 km. With what speed should this satellite be projected into orbit? What will be the time period?
Take g at the surface `=9.8ms^-2` and radius of the earth =6400 km.
View SolutionAssume the radius of the earth to be `6.4xx10^(6)m`
a. Calculate the time period `T` of a satellite on equational orbit at `1.4xx10^(e)m` above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?
View SolutionA satellite of mass `2xx10^(3)kg` has to be shifted from an orbit of radius 2R to another of radius 3R, where R is the radius of the earth. Calculate the minimum energy required. Take mass of earth `=6xx10^(24)kg`, radius of earth `=6.4xx10^(6)m`.
View SolutionA double star is a system of two starts moving around the centre of inertia of the system due to gravitation. Find the distance between the components of the double star, if its total mass equals M and the period of revolution T.
View SolutionIf a planet was suddenly stopped in its orbit supposed to be circular, show that it would fall onto the sun in a time `sqrt(2)/(8)` times the period of the plant's revolution.
View SolutionA particle takes a time `t_(1)` to move down a straight tunnel from the surface of earth to its centre. If gravity were to remain constant this time would be `t_(2)` calculate the ratio `(t_(1))/(t_(2))`
View SolutionA planet of mass M moves around the Sun along an ellipse so that its minimum distance from the Sun is equal to r and the maximum distance to R. Making use of Kepler's laws, find its period of revolution around the Sun.
View SolutionSuppose we have made a model of the Solar system scaled down in the ratio `eta` but of materials of the same mean density as the actual materials of the planets and the Sun. How will the orbital periods of revolution of planetary models change in this case?
View SolutionTwo Earth's satellites move in a common plane along circular orbits. The orbital radius of one satellite `r=700km` while that of the other satellite is `Deltar=70km` less. What time interval separates the periodic approaches of the satellites to each other over the minimum distance?
View SolutionA satellite is put in an orbit just above the earth's atmosphere with a velocity `sqrt(1.5)` times the velocity for a circular orbit at the that height. The initial velocity imparted is horizontal. What would be the maximum distance of the satellite from the earth, when it is in the orbit.
View SolutionA cosmic body `A` moves to the sun with velocity `v_(0)`(when far from the sun) and aiming parameter `l`, the arm of the vector `v_(0)`, relative to the centre of the sun. find the minimum distance by which this body will get to the sun. mass of the sum is `M`.
View SolutionTwo satellites `S_(1)` and `S_(2)` revolve round a planet in coplaner circular orbit in the same sense. Their period of revolution are `1` hour and `8` hour respectively. The radius of the orbit of `S_(1)` is `10^(4) km`. When `S_(2)` is closest to `S_(1)`, find
(a) The speed of `S_(2)` relative to `S_(1)`,
(b) The angular speed of `S_(2)` actually observed by an astronaut is `S_(1)`
View SolutionIf a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is `r_(1)` and maximum distance is `r_(2)`. Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse.
View SolutionFor a low altitude orbit if `r ~= r_(p)`, where `r_(p)` is planet radius, show that for a given average planetary density, the orbital period of satellite is independent of the size of the planet. Calculate its value average density is `rho`.
View SolutionWhat should be the orbit radius of a communication satellite that it can cover 75% of the surface area of earth during its revolution.
View SolutionThe radius of a planet is `R_1 `and a satellite revolves round it in a circle of radius `R_2`. The time period of revolution is T. find the acceleration due to the gravitational force of the plane at its surface.
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of `1` year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is `r` and the distance of the earth from the Sun is `R`, find the relation between `r` and `R`.
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed of equal to half the magnitude of escape velocity from earth.
(i). Determine the height of the satellite above the earth's surface
(ii). If the satellite is stopped suddenly in its orbit and allowed to fall freely on the earth. Find the speed with it hits and surface of earth. Given `M="mass of earth & R "="Radius of earth"
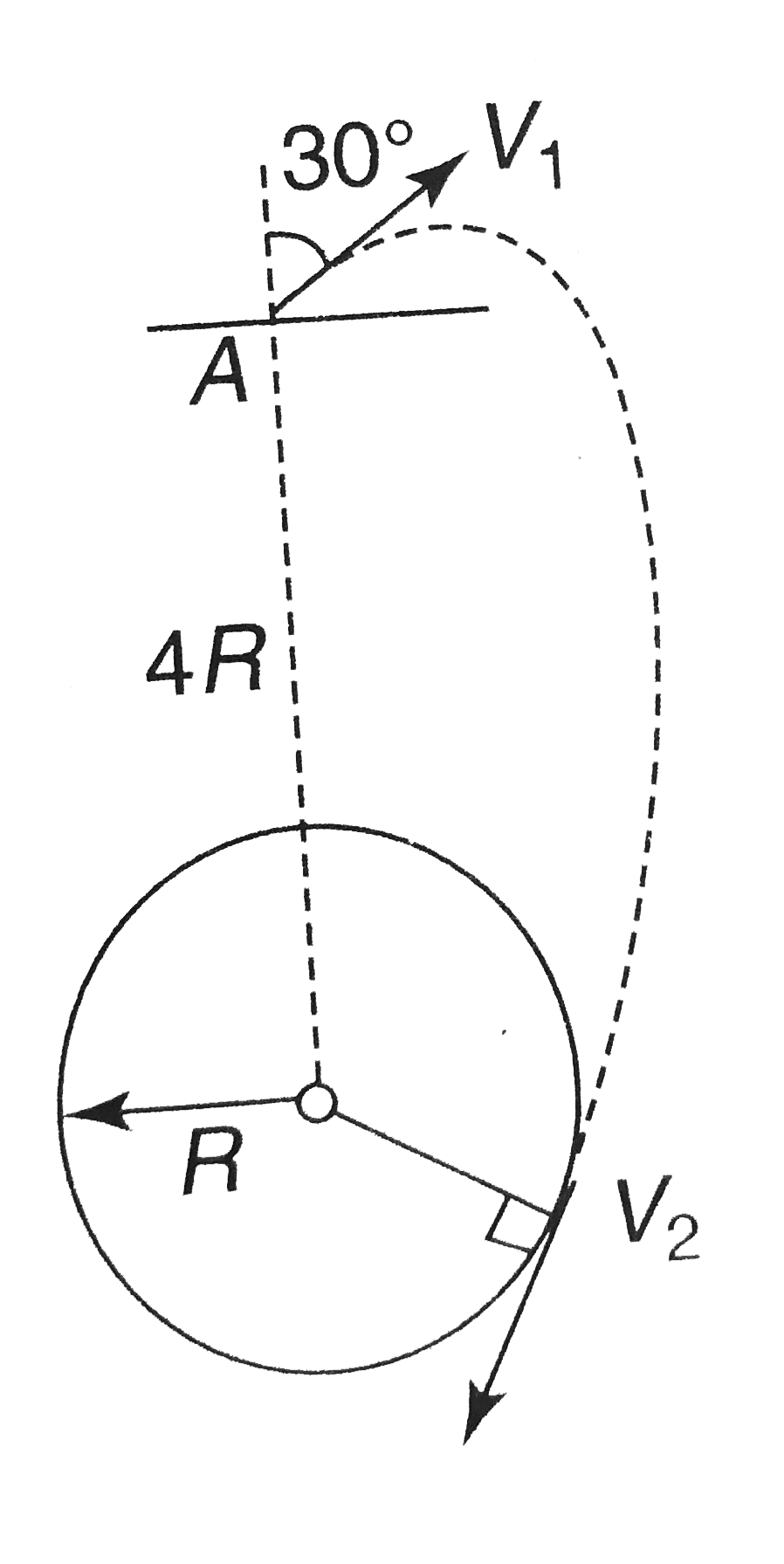
View SolutionA particle is projected from point `A`, that is at a distance `4R` form the centre of the earth, with speed `V_(1)` in a direction making `30^(@)` with the line joining the centre of the earth and point `A`, as shown. Consider gravitational interaction only between thesetwo. (Use `(GM)/R=6.4xx10^(7) m^(2)//s^(2)`). The speed `V_(1)` if particle pasess grazing the surface of the earth is
View SolutionA mass of `6xx10^(24) kg` is to be compressed in a sphere in such a way that the escape velocity from its surface is `3xx10^(8) m//s`. Find the radius of the sphere (in `mm`).
View Solution
Particle Exercise questions and complete solutions for chapter GRAVITATION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11