Complete Solutions to Unsolved Numerical of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| PHYSICS GALAXY | Unsolved Numerical |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
At what distance from the center of the earth will a 1 kg object have a weight of `1 N` ? If released from rest at this distance, What will its initial acceleration be ?
View SolutionThe radius of Mars is `3.4 xx 10^(6)m` and the accelerationof a freely falling object on its surface is `3.7 m//s^(2)`. Determine the mass of Mars.
View SolutionSuppose we invent a unit of mass which we shall call the caendish (C). One cavendish of mass is defined such that `G = 1.0000(AU)^(3)//(yr^(2)C)`. Our unit of length is the astronomical unit `(AU)`, the earth-sun distance`-1AU = 1.496 xx 10^(11) m`- and our unit of time is the year `(yr)`. (a) Datermine the conversion factor between C and kg. (b) Find the mass of the sun in C.
View SolutionDetermine the fractional reduction of the acceleration of gravity due to an increase in elevation of `10 km` neart the earth's surface.
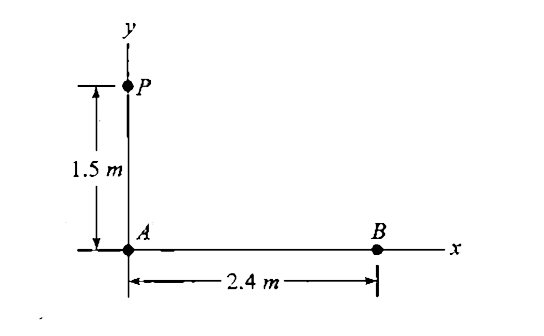
View SolutionIn figure-6.105, particle A has a mass of `1.4` and particle B has a mass of `3.1 kg`. What is the gravitational field at point P ?
View SolutionWhile investigating the planet Norc in another solar system, we find that the radius of Norc is `9.54 xx 10^(6) m` and that the period of a satellite put in circular orbit of radius `1.476 xx 10^(7) m` is `8.09 xx 10^(3) s`. Determine (a) the mass of Norc, (b) The average, mass density of Norc, (c) the value of the gravitational field on the surface of Norc. (d) If the period of Norc's rotation about its axis is `1.04 xx 10^(4) s`, what will be the reading on a spring scale (calibrated on earth) supporting a `1.0 kg` object at Norc's equator ?
View SolutionTwo concentric shells of mass `m_(1)` and `m_(2)` are situated as shown. Find the force on a particle of mass `m` when the particles is located at `(a) r=r_(1),(b)r=r_(2),(c)r=r_(3)`. The distance `r` is measured from the centre of the shell.

View SolutionTwo point masses, each equal to M, are placed a distance `2a` apart. Show that a small mass m placed midway between them on the line joining them will be in equilibrium and if it is slightly displaced from this position along the line perpendicular to the line joining the masses, it will execute simple harmonic oscillations. Calculate the frequnency of these oscillations.
View SolutionComputer the mass and density of the moon if acceleration due to gravity on its surfac is `1.62 m//s^(2)` and its radius is `1.74 xx 10^(6)m[G = 6.67 xx 10^(-11) MKS` units].
View SolutionTwo masses `m_(1)` and `m_(2)` at an infinite distance from each other are initially at rest, start interacting gravitationally. Find their velocity of approach when they are at a distance `r` apart.
View SolutionImagine a planet whose diameter and mass are both one half of those of earth. The day's temperature of this planet surface reaches upto `800 K`. ? Make calculation and tell whether oxygen molecules are possible in the atmosohere of the planet.
[Escape velocity from earth's surface `= 11.2 km//s, k = 1.38 xx 10^(-23)J//K`, mass of oxygen molecule `= 5.3 xx 10^(-26) kg`].
View SolutionA thin rod of mass M and length L is bent in a semicircle as shown in figure (a). What is its gravitational force (both magnitude and direction) on a particle with mass m at O the centre of curvature ? (b) what would be the force on m if the rod is in the form of complete circle?
View SolutionThree identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is released from the surface of earth along tunnel. Coefficient of restitution for collision between soil at centre and ball is `0.5`. Calculate the distance travelled by ball just before second collision at centre. Given mass of the earth is `M` and radius of the earth is `R`.
View SolutionA particle of mass `m` is subjected to an attractive central force of magnitude `k//r^(2)`, `k` being a constant. If at the instant when the particle is at an extreme position in its closed orbit, at a distance a from the centre of force, its speed is `sqrt(k//2ma)`, if the distance of other extreme position is b. Find `a//b`.
View SolutionIf the radius of the earth were to shrink by one percent its mass remaining the same, the acceleration due to greavity on the earth's surface would
View SolutionIn a certain region of space gravitational field is given by `I = - (k//r)`. Taking the reference point to be at `r = r_(0)`, with gravitational potential `V = V_(0)`, find the gravitational potential at distance `r`.
View SolutionA short , straight and frictinless tunnel is bored through the centre of the earth and a body is realesed from the surface into the tunnel . Show that the motion of the body in the tunnell will be simple harmoic and hence calculate the taken by the body to travel from one end of the tunnel to the other (Radius of the earth = `6.38 xx 10^(6)m` and acceleration due to gravity at the surface = `9.81 ms^(2)`
View SolutionAn iron ball o fradius 1 m and density `8000 kg m^(-3)` is placed in water . A bubble of radius 1 cm at a distance 1.5 m from the centre of the ball . Will there be a force of attraction or repulsion between them and what will be the magnitude of this force ? (Neglect the mass of air and take ` G=6.67 xx 10^(-11)`.)
View SolutionTwo satellites `A` and `B` of equal mass move in the equatorial plane of the earth, close to earth's surface. Satellite `A` moves in the same direction as the of the rotation of the earth while satellite `B` moves in the opposite direction. Calclate the ratio of the kinetic energy of `B` of that of `A` in the reference frame fixed to the earth `(g=9.8ms^(-2)` and radius of the earth `=6.37xx10^(6)km)`
View SolutionThree masses, `100 kg, 200 kg` and `500 kg` are placed at the vertices of an equilibrium triangle with sides `10 m`. They are rerranged by an agent on the vertices of a bigger triangle of sides `15m` and with the same in-centre. Calculate the work done by the agent.
View SolutionA satellite of Sun is in a circular orbit around the Sun, midway between the Suna and earth. Find the period of this satellite.
View SolutionA spacecraft is in a circular orbitof radius `3R` around the moon as shown in figure-6.109. At point A, the spacraft fires a probe which is supposed to arrive at the surface of the moon at point B. Datermine the necessary velocity `v_(r)` of the probe relative to the spacecraft just fter ejection. Also calculate the angular displacement `theta` of the spacecraft when the probe arrives at point B. Assume velocity of spacecraft remains unchanged due to ejection of probe.

View SolutionAn object weighs `10 N` at north pole of Earth. In a geostationary satellite distance `7 R` from centre of Earth (of radius `R`), what will be its (a) true weight (b) apparent weight?
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionWhat will be acceleration due to gravity on the surface of the moon if its radius were `(1//4)^(th)` the radius of earth and its mass `(1//80)^(th)` the mass of earth? What will be the escape velocity on the surface of moon if it is `11.2 km//s` on the surface of the earth? (given that `g=9.8 m//s^(2)`)
View SolutionIn a gravitational field `vectorg = (2hati + 3hatj) N//kg`. What is the work done in moving particle from `(1,1)` to `(2,1//3)` along the line `2x + 3 y = 5`.
View SolutionA satellite is revolving in the circular equatorial orbit of radius `R=2xx10^(4)km` from east to west. Calculate the interval after which it will appear at the same equatorial town. Given that the radius of the earth `=6400km` and `g` (acceleration due to gravity) `=10ms^(-2)`
View SolutionA system consists of a thin ring of radius R and a very long uniform wire oriented along axis of the ring with one of its ends coinciding with the centre of the ring. If mass of ring be M and mass of wire be `lambda` per unit length, calculate interaction force between the ring and the wire.
View SolutionA pendulum beats seconds on the surface of the Earth. Calculate as to how much it loses or gains per day if it is taken to,
(a) a mass 8 km below,
(b) a point 8 km above, the surface. (Radius of the Earth `= 6.4 xx 10^(6)m`)
View SolutionThe ratio of the K.E. required to the given to the satellite to escape earth's gravitational field to the K.E. required to be given so that the satellite moves in a circular orbit just above earth atmosphere is
View SolutionIf the time period of a satellite `T_(S)` is different from that of earth's rotation `T_(E)` and the satellite is moving in the direction of earth's rotation, show that the time interval between two successive appearances of the satellite overhead is given by ltbRgt `(1)/(T) = (1)/(T_(S)) ~ (1)/(T_(E))`
What will happen to this interval if `T_(S) = T_(E)`
View SolutionTwo identical solid copper spheres of radius `R` placed in contact with each other. The gravitational attracton between them is proportional to
View SolutionThe masses and radii of the Earth and the Moon are `M_1, R_1 and M_2,R_2` respectively. Their centres are at a distance d apart. The minimum speed with which a particel of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View SolutionA `50` kg astronaut is floating at rest in space `35 m` from her stationary `150,000` kg spaceship. About how long will it take her to float to the ship under the action of the force of gravity?
View SolutionThe eccentricity of the earth's orbit is `0.0167`, the ratio of its maximum speed in its orbit to its minimum speed is
View SolutionFind the proper potential energy of gravitational interaction of matter forming
(a) a thin uniform spherical layer of mass m and radius R,
(b) a uniform sphere of mass m and radius R(make use of the answer to Problem)
View SolutionA man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface realizes that he will pass through a small hole in the planet. As he enters the hole he seen that the planet really made of two places a spherical shell of negligible thickness of mass `(2M)/(3)` and a point mass `(M)/(3)` of centre. Change in the force of gravity experienced by the man is
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass `M` and the other `m`. Their centres are a distance `d` apart, `d` being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionA planet of mass M moves around the Sun along an ellipse so that its minimum distance from the Sun is equal to r and the maximum distance to R. Making use of Kepler's laws, find its period of revolution around the Sun.
View SolutionThe optimal way of transferring a space vehicle from an inner circular orbit to an outer coplanar circular orbit is to fire its engines as it passes through A to increase its speed and place it in an elliptic transfer orbit. Another increase in speed as it passes through B will place it in the desired circular orbit. For a vehicle in a circular orbit about the earth at an altitude `h_(1) = 320 km`, which is to be transferred to a circular orbit at an altitude `h_(2) = 800 km`, determine :
(a) The required increases in speed at A and B.
(b) The total energy per unit mass required to execute the

View SolutionA lunar probe is rocketed from earth directly toward the moon in such a way that it always between the earth and the moon. The probe narrowly misses the moon and continues to travel beyond it on an extension of the line segement described above. At what distance from the center of the earth will the force due to the earth be equal to the force due to the moon?
View SolutionA particle is projected from earth surface with a velocity `sqrt((4gR)/(3))` in upward direction where R is the radius of earth. Find the velocity of particle when it is at half its maximum height.
View SolutionA rocket starts vertically upward with speed `v_(0)`. Show that its speed `v` at height `h` is given by `v_(0)^(2)-v^(2)=(2hg)/(1+h/R)`
where `R` is the radius of the earth and `g` is acceleration due to gravity at earth's suface. Deduce an expression for maximum height reachhed by a rocket fired with speed `0.9` times the escape velocity.
View SolutionA satellite is in a circular orbit very close to the surface of a planet. At some point it is given an impulse along its direction of motion, causing its velocity to increase `n` times . It now goes into an elliptical orbit. The maximum possible value of `n` for this to occur is
View SolutionA spherical hollow is made in lead sphere of radius R, such that its surface touche the outside surface of the lead sphere and passes though its centre. The mass of the sphere before hollowing sphere exert on a point mass m placed at the centre of the hollow?

View SolutionIf a satellites is revolving close to a planet of density `rho` with period `T`, show that the quantity `rho T^(2)` is a universal constant.
View SolutionFind the angular speed of earth so that a body lying at `30^(@)` latitude may become weightless.
View SolutionA projectile is fired vertically upwards from the surface of the earth with a velocity `Kv_(e)`, where `v_(e)` is the escape velocity and `Klt1`.If `R` is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)
View SolutionA satellite is in a circular polar orbit of altitude `300 km`. Determine the sparation d at the equator between the ground tracks associated with two successive overhead passes of the satellite.
View SolutionA satellite of mass `5M` orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass `M` and the other of masses `4M`. After the explosion the mass `M` ends up travelling in the same circular orbit, but in the opposite direction. After explosion the mass `4M` is
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height `h`.
View SolutionWhat is the radius of a planet of density `rho` if at its surface escape velocity of a body is `v`.
View SolutionConsider two satellites `A` and `B` of equal mass, moving in the same circular orbit of radius `r` around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy `E_(A) + E_(B)` of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
View SolutionA satellite is moving around the earth's with speed `v` in a circular orbit of radius `r`. If the orbit radius is decreases by `1%` , its speed will
View SolutionA body on the equaotr of a planet weighs half of its weight at the pole. The density of matter of the planet is `3g//cm^(3)`. Determine the peiod of rotation of the planet about its axis.
View SolutionTwo satellites move in circular orbits around the earth at distances `9000 km` and `9010 km` from earth's centre. If the satellite which is moving faster has a period of revolution `90` minutes. Find the difference in their revolution periods.
View SolutionA body Is projected horizontally near the surface of the earth with `sqrt(1.5)` times the orbital velocity. Calculate the maximum height up to which it will rise above the surface of the earth.
View SolutionA satellite is orbiting around earth with its orbit radius `16` times as great as that of parking satellite. What is the period of this satellite.
View SolutionWhat should be the radius of a planet with mass equal to that of earth and escape velocity on its surface is equal to the velocity of light. Given that mass of earth is `M=6xx10^(24)kg`.
View SolutionTreating the earth as a symmetrical sphere of radius `R = 6400 km` with field `9.8 N//kg` at its surface, calcualate the vertical speed with which a rocket should be fired so as to reach a height `4R` from the surface.
View SolutionA diametrical tunnel is dug across the earth. A ball dropped into the tunnel from one side. The velocity of the ball when it reaches the centre of the earth is [Given: gravitational potential at the centre of earth `= -3//2(GM//R)`]
View SolutionTwo satellite `S_(1)` and `S_(2)` revolve around a planet in coplanar circular orbits in the opposite sense. The periods of revolutions are `T` and `eta T` respectively. Find the angular speed of `S_(2)` as observed by an astronouts in `S_(1)`, are observed by an astronaut in `S_(1)`, when they are closest to each other.
View SolutionA small body starts falling onto the Sun from a distance equal to the radius of the Earth's orbit. The initial velocity of the body is equal to zero in the heliocentric reference frame. Making use of Kepler's laws, find how long the body will be falling.
View SolutionGravitational potential difference between surface of a planet and a point situated at a height of 20 m above its surface is 2joule/kg. if gravitational field is uniform, then the work done in taking a 5kg body of height 4 meter above surface will be-:
View SolutionWhat woluld be the length of a day. If angular speed of earth is increased such that bodies typing on the equator by off?
View SolutionA communication satellite is put in parking orbit. What is the time taken by a wave to go to satellite and come back to earth in its checking mode.
View SolutionA cord of length `64 m` is used to connected a `100 kg` astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is `6400 km`.
View SolutionThe escape velocity for a planet is `20 km//s`. Find the potential energy of a particle of mss `1 kg`on the surface of this planet.
View SolutionA particle of mass `1kg` is placed at a distance of `4m` from the centre and on the axis of a uniform ring mass `5kg` and radius `3m`. The work done to increase the distance of the particle from `4m` to `3sqrt(3)`m is
View SolutionA body of mass `m` rises to a height `h=R//5` from the earth's surface where `R` is earth's radius. If `g` is acceleration due to gravity at the earth's surface, the increase in potential energy is
View SolutionA missile which missed its target went into an orbit around the earth at a mean radius `4` times great as the parking orbit. Find the period of missile
View SolutionCompute the magnitude of the necessary launch velocity at B and angle `alpha`. If the projectile trajectory is to intersect the earth's surface so that the angle `beta` equals `90^(@)`. The altitude at the highest point of the trajectory is `0.5 R`.

View SolutionSuppose Moon's orbital motion around the earth is suddenly stopped. Making use of Kepler's third law find the time the moon shell take to fall on to the earth?
View SolutionDistance between the centres of two stars is `10alpha.` The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.
View SolutionIf a body is to be projected vertically upwards from earth's surface to reach a height of `10R` where `R` is the radius of earth. The velocity required to be is
View SolutionA satellite of mass , os revolving round the eartj at height of `10R`, where R is the radius of earth. What is the kinetic energy of satellite.
View SolutionA sapceship nears the Moon along a parabolic trajectory that almost toches the Moon's surface. In order to transfer closest approach. The engine ejects gas ata speed of `u = 4 km//s` realtive to the spaceship In its direction of motion. If `v_(1) =` velocity of spaceship in parabolic trajectory, when it almost touches the earth and `v_(2) =` velocity of spaceship in circular orbit when it almost to'uches the earth. Then what friction of total mass should the fuel burn to transfer space ship to circular orbit?
View SolutionIf Earth be at one half its present distance from the sun, how many days will there be in a year?
View SolutionAt what height from the ground will the value of ‘ g ’ be the same as that in 10 km deep mine below the surface of earth
View SolutionA Body moving radially away from a planet of mas M, when at distance r from planet, explodes in such a way that two of its many fragments move in mutually prependicular circular orbits around the planet what will be
(i). Then velocity in circular orbits?
(ii). Maximum distance between the two fragments before collision and
(iii). Magnitude of their relative velocity just before they collide?
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by `h`. The error in weighing in terms of density of the earth `rho` is
View SolutionThe acceleration due to gravity about the earth's surface would be half of its value on the surface of the earth at an altitude of ( R = 4000 mile )
View SolutionA ring of radius `R = 4m` is made of a highly dense material. Mass of the ring is `m_(1) = 5.4 xx 10^(9) kg` distributed uniformly over its circumference. A highly dense particle of mass `m_(2) = 6 xx 10^(8) kg` is placed on the axis of the ring at a distance `x_(0) = 3 m` from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionFor particles of equal masses M that move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionThe density of the core a planet is `rho_(1)` and that of the outer shell is `rho_(2)`. The radii of the core and that of the planet are `R` and `2R` respectively. The acceleration due to gravity at the surface of the planet is same as at a depth `R`. Find the ratio of `(rho_(1))/(rho_(2))`

View SolutionA planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance `r_0` from the Sun its velocity was equal to `v_0` and the angle between the radius vector `r_0` and the velocity vector `v_0` was equal to `alpha`. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View SolutionIf gravitational forces between a planet and a satellite is proportional to `R^(-5//2)`. If R is the orbit radius. Then the period of revolution of satellites is proportional to `R^(n)`. Find n.
View SolutionA uniform sphere of radius a and density `rho` is divided in two parts by a plane at a distance `b` from its centre. Calculate the mutual attraction between two parts.
View SolutionA uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
View SolutionA meteorite approaching a planet of mass M (in the straight line passing through the centre of the planet) collides with an automatic space station orbiting the planet in a circular trajectory of radius R. The mass of the station is ten times as large as the mass of the meteorite. As a result of the collision, the meteorite sticks in the station which goes over to a new orbit with the minimum distance R/2 from the planet. Speed of the meteorite just before it collides with the planet is : .
View SolutionTwo satellites of the earth move in the sme plane with radii a and b,b being slghtly gerater than a. what is the minimum intants when they are on the same line thourth the centre of the earth (i) when they move in the same direction ,(ii) in oppsite direction?
View SolutionTwo lead spheres of `20 cm` and `2 cm` diametre respectively are planet with centres `100 cm` apart. Calculate the attraction between them, given the radius of the Earth as `6.37 xx 10^(8) cm` and its mean density as `5.53 xx 10^(3) kg m^(-3)`. Speciffic gravity of lead `= 11.5`. If the lead spheres are replaced by bress sphere of the same radii, would the force of attraction be the same?
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View Solution
Unsolved Numerical questions and complete solutions for chapter GRAVITATION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11