Complete Solutions to Numerial MCQs of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| PHYSICS GALAXY | Numerial MCQs |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
The ratio of the time period of a simple pendulum of length `l_(0)` with a pendulum of infinite length is :
(Where, R is the radius of earth)
View SolutionThe rotation of the earth radius R about its axis speeds upto a value such that a man at latitude angle `60^(@)` feels weightless. The duration of the day in such case will be
View SolutionAt what height the gravitationa field reduces by `75%` of the gravitational field at the surface of earth?
View SolutionIn a certain region of space, the gravitational field is given by `-(k)/(r)` where `r` is the distance and k is a constant. If the gravitaional potential at `r=r_(0)` be `V_(0)`, then what is the expression for the gravitaional potential (V)-
View SolutionIf different planets have the same density but diferent radii then the acceleration due to gravity (g) on the surface of the planet will depend on its radius (R) as
View SolutionA shell of mass M and radius R has another point mass m placed at a distance r from its centre `(r gt R)`. The force of attraction between the shell and point mass is :
View SolutionLet the acceleration due to gravity be `g_(1)` at a height `h` above the earth's surface `g_(2)` at a depth `d` below the earth's surface. If `g_(1)=g_(2),h lt lt R` and `d lt lt R` then
View SolutionA satellite is revolving round the earth in an orbit of radius r with time period T. If the satellite is revolving round the earth in an orbit of radius `r + Deltar(Deltar lt lt r)` with time period `T + DeltaT(DeltaT lt lt T)` then.
View SolutionConsider an infinite plane sheet of mass with surface mass density `sigma`. The gravitational field intensity at a point P at perpendicular distance r from such a sheet is :
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If `Q_1` coulomb, and `Q_2` coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionA point P `(Rsqrt(3)m,0,)` lies on the axis of a ring of mass M and radius R. The ring is located in `y -z` plane with its centre at origin. A small particle of mass m start from P and reaches O under gravitational attraction only. Its speed at O will be.
View SolutionAn artificial satellite moving in circular orbit around the earth has total (kinetic + potential) energy `E_(0)`. Its potential energy and kinetic energy respectively are :
View SolutionThe ratio of the earth's orbital angular momentum (about the Sun) to its mass is `4.4 xx 10^(15) m^(2) s^(-1)`. The area enclosed by the earth's orbit is approximately-___________m^(2).
View SolutionA particle is projected vertivally upwards from the surface of earth `(radius R_e)` with a kinetic energy equal to half of the minimum value needed for it to escape. The height to which it rises above the surface of earth is ……
View SolutionA satellite of mass `5000kg` is projected in space with an intial speed of `400m//s` making an angle of `30^(@)` with the radial direaction from a distance `3.6 xx 10^(7) m` away from the center of the earth.
The angular momentum of satellite :
View SolutionA satellite of mass `5000kg` is projected in space with an intial speed of `400m//s` making an angle of `30^(@)` with the radial direaction from a distance `3.6 xx 10^(7) m` away from the center of the earth.
The energy of satellite :
View SolutionA satellite of mass `5000kg` is projected in space with an intial speed of `400m//s` making an angle of `30^(@)` with the radial direaction from a distance `3.6 xx 10^(7) m` away from the center of the earth.
The minimum distance of state
The minimum distance of satellite from earth :
View SolutionA satellite of mass `5000kg` is projected in space with an intial speed of `400m//s` making an angle of `30^(@)` with the radial direaction from a distance `3.6 xx 10^(7) m` away from the center of the earth.
The maximum distance of satellite from earth.
View SolutionA satellite of mass `5000kg` is projected in space with an intial speed of `400m//s` making an angle of `30^(@)` with the radial direaction from a distance `3.6 xx 10^(7) m` away from the center of the earth.
The semi-major axis of the orbit of satellite :
View SolutionSemi-major axis of the orbita of satellite :
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius r with a period of revolution T. On what power of r will the square of time period will depend if the gravitational force of attraction between the planet and the star is proportional to `r^(-5//2)`.
View SolutionA projectile is fired from the surface of earth of radius `R` with a velocity `k upsilon_(e)` (where `upsilon_(e)` is the escape velocity from surface of earth and `k lt 1)`. Neglecting air resistance, the maximum height of rise from centre of earth is
View SolutionTwo satellites `S_(1)` and `S_(2)` revolve around a planet in coplanar circular orbits in the same sense their periods of revolution are 1 hour and 8hours respectively the radius of the orbit of `S_(1)` is `10^(4)` km when `S_(1)` is closest to `S_(2)` the angular speed of `S_(2)` as observed by an astronaut in `S_(1)` is :
View SolutionIn previous problem what is the angular speed of `S_(2)` is the observed by an astronaut in `S_(1)` when they are closet :
View SolutionTwo particles of masses `m_(1)` and `m_(2)` initially at rest a infinite distance from each other, move under the action of mutual gravitational pull. Show that at any instant therir relative velocity of approach is `sqrt(2G(m_(1)+m_(2))//R)` where `R` is their separation at that instant.
View SolutionA body is imparted a velocity v from the surface of the earth. If `v_(0)` is orbital velocity and `v_(e)` be the escape velocity then for :
`v = v_(0)` the body follows a circular track around the earth.
(B). `v gt v_(0)` but `lt ve`, the body follows elliptical path around the earth.
(C). `v lt v_(0)`, the body follows elliptical path and return to surface of earth.
(D). `v gt v_(e)`, the body follows hyperbolic path and escape the gravitational pull of the earth.
View SolutionThe escape velocity for a planet is `v_e`. A particle is projected from its surface with a speed `v`. For this particle to move as a satellite around the planet.
View SolutionTwo bodies of masses m and M are placed at distance d apart. The gravitational potential (V) at the position where the gravitational field due to them is zero V is
View SolutionSuppose we have made a model of the Solar system scaled down in the ratio `eta` but of materials of the same mean density as the actual materials of the planets and the Sun. How will the orbital periods of revolution of planetary models change in this case?
View SolutionA geostationary satellite orbits around the earth in a circular orbit of radius 36,000 km. then the time period of a spy satellite orbiting a few hundred km (600 km) above the earth's surface (R=6400 km) will approximately be
View SolutionConsider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
View SolutionFind the proper potential energy of gravitational interaction of matter forming
(a) a thin uniform spherical layer of mass m and radius R,
(b) a uniform sphere of mass m and radius R(make use of the answer to Problem)
View SolutionWhat should be the period of rotation of earth so as to make any object on the equator weig half of its present value?
View SolutionAn artificial satellite is describing an equatorial orbit at `3600 km` above the earth's surface. Calculate its period of revolution? Take earth radius `6400km`.
View SolutionIn previous question calculate orbital speed of satellite.
View SolutionFind the work done in bringing three particles each having a mass of 100 g, from large distances to the vertices of an equilateral triangle of side 20 cm.
View SolutionIn a satellite if the time of revolution is `T`, then kinetic energy is proportional to
View SolutionA saturn year is 29.5 times the earth year. How far is the saturn from the sun if the earth is `1.5xx10^(8)` away from the sun?
View SolutionA spherical planet far out in space has a mass `M_(0)` and diameter `D_(0)`. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
View SolutionA body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity on reaching the surface of earth. Take `g=` acceleration due to gravity on the surface of the Earth.
View SolutionTwo satellite A and B are moving round a planet in circular orbit having radii R and 3R respectively, if the speed of satellite A is v the speed f satellite B will be :
View SolutionThe radius of a planet is `R`. A satellite revolves around it in a circle of radius `r` with angular velocity `omega_(0)`. The acceleration due to the gravity on planet's surface is
View SolutionThe gravitational field in a in region is given by `vecg = (4hati + vecj) N//kg`. What done by this field is zero when the particle is moved along the line :
View SolutionThe figure shows a spherical shell of mass `M`. The point `A` is not at the centre but away from the centre of the shell. If a particle of mass `m` is placed at `A`, then

View SolutionSupernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than `1.4` times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius `R_(S)`, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius `R_(S)`. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about `6` light years. that orbits this massive object with an orbital speed of about `2 xx 10^(5) m//s`. Use the given data whereever necessary and answer the questions that hollow. `G = 6.67 xx 10^(-11) N - m^(2)//kg^(2)`, Solar mass `M = 2 xx 10^(30) kg, C = 3 xx 10^(8) m//s, 1` light year `= 9.5 xx 10^(15) m`.
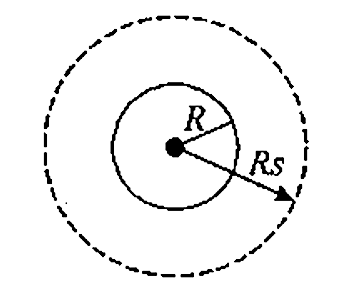
Mass (in kg) of the massive object at the centre of the milky galaxy is of the order :
View SolutionSupernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than `1.4` times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius `R_(S)`, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius `R_(S)`. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about `6` light years. that orbits this massive object with an orbital speed of about `2 xx 10^(5) m//s`. Use the given data whereever necessary and answer the questions that hollow. `G = 6.67 xx 10^(-11) N - m^(2)//kg^(2)`, Solar mass `M = 2 xx 10^(30) kg, C = 3 xx 10^(8) m//s, 1` light year `= 9.5 xx 10^(15) m`.
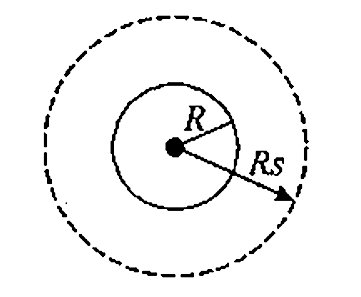
Theories suggest that it is not possible for a single star to have a mass of more than `50` masses. The massive object at the centre of milky way galaxy is most likely to be a :
View SolutionSupernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than `1.4` times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius `R_(S)`, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius `R_(S)`. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about `6` light years. that orbits this massive object with an orbital speed of about `2 xx 10^(5) m//s`. Use the given data whereever necessary and answer the questions that hollow. `G = 6.67 xx 10^(-11) N - m^(2)//kg^(2)`, Solar mass `M = 2 xx 10^(30) kg, C = 3 xx 10^(8) m//s, 1` light year `= 9.5 xx 10^(15) m`.
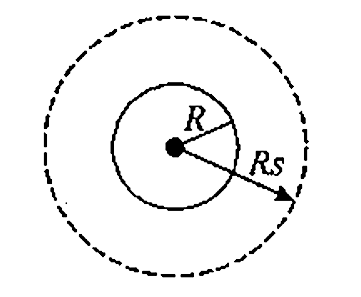
If mass of earth `M_(E) ~~ 6 xx 10^(24) kg` and its radius `R_(E) = 6400 km`, to what fraction of its presents radius does the earth need to be compressed in order to become a black hole ?
(Give only the order of your answer)
View SolutionA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth `v_(e)` is :
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle `theta` that the threads will make with the vertical due to attraction between the balls is :
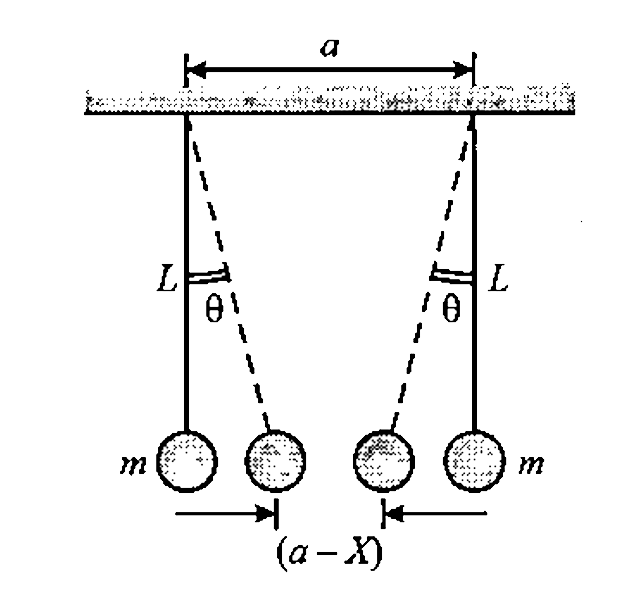
View SolutionTwo masses of mass m each are fixed at a separation distance of `2d`. A small mass `m_(s)` placed midway, when displaced slightly, starts oscillating. Then :
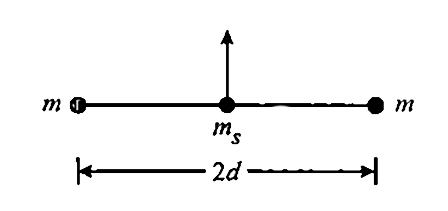
View SolutionMass M is uniformly distributed only on curved surface of a thin hemispherical shell. A, B and C are three points on the circular base of hemisphere, such that A is the centre. Let the gravitational potential at poins A, B and C be `V_(A), V_(B), V_(C)` respectively. Then :

View SolutionFigure shows a uniformly charges hemispherical shell. The direction of electric field at point `p` that is off centre (but in the plane of the largest circle of the hemisphere), will be along

View SolutionA straight rod of length `L` extends from `x=a` to `x=L+a`. Find the gravitational force exerts on a point mass `m` at `x=0` is (if the linear density of rod`mu=A+Bx^(2)`)
View SolutionThe planets with radii `R_(1)` and `R_(2)` have densities `p_(1),p_(2)` respectively. Their atmospheric pressues are `p_(1)` and `p_(2)` respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
View SolutionA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance `r_(a)` and perihelion distance `r_(p)`. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are `(r_(a) + r_(p))/(2)` and `sqrt(rho_(p)r_(a))` respectively. The angular momentum of the satellite is :
View SolutionA uniform thin rod of mass `m` and length `R` is placed normally on surface of earth as shown. The mass of earth is `M` and its radius `R`. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
View SolutionConsider a mass `m_(0)` enclosed by a closed imaginary surface S. Let `vec(g)` be the gravitational field intensity due to `m_(0)` at the surface element `d vec(S)` directed as outward normal to it. The surface integral of the gravitational field over S is :
View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
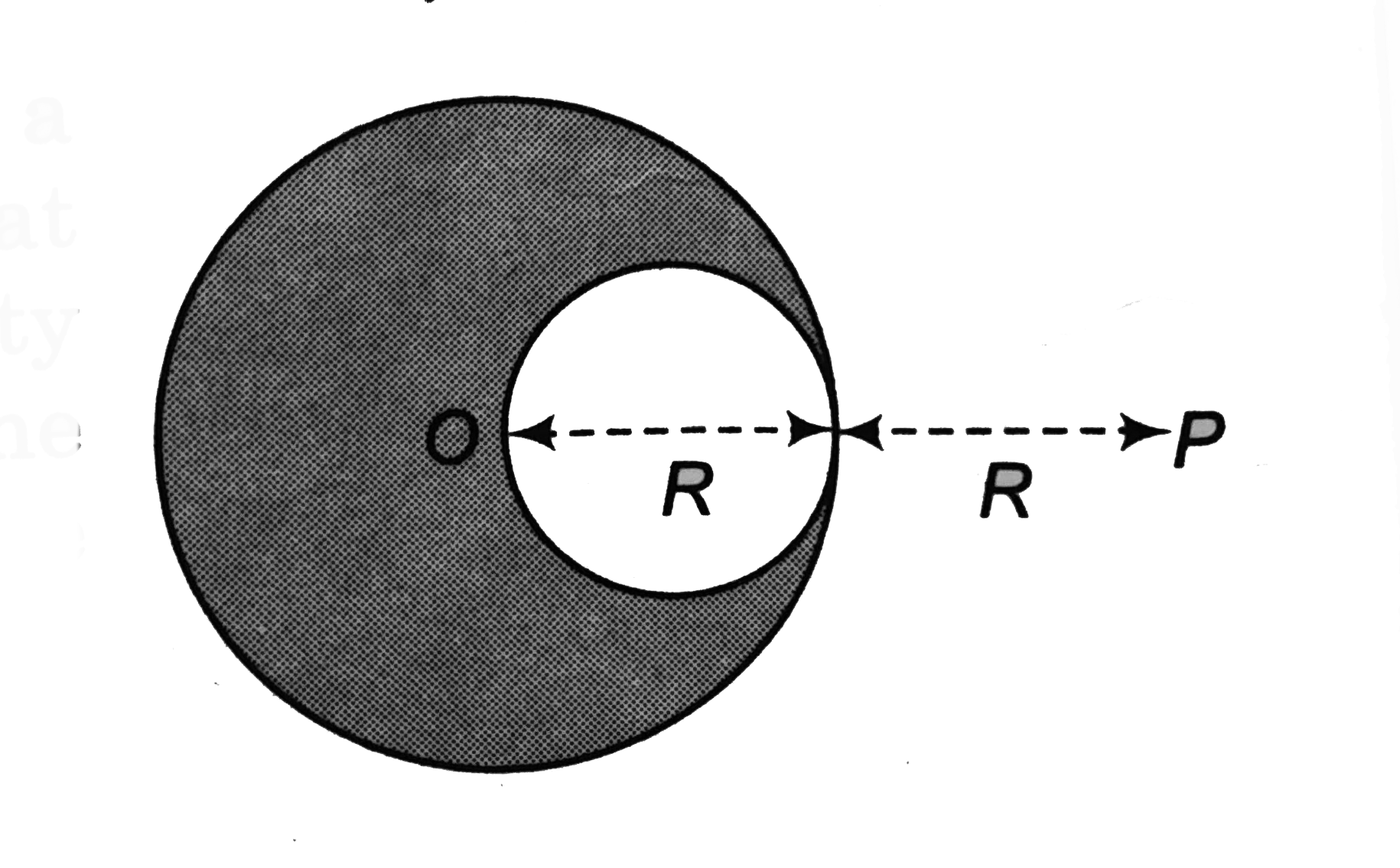
View Solution
Numerial MCQs questions and complete solutions for chapter GRAVITATION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11