Complete Solutions to 6 Long answer (NCERT) of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PRADEEP | 6 Long answer (NCERT) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
A hill is ` 500 m` hight. Supplies are to be across the hill using a canon that can hurl packetets at a speed of `125 m//s` pver the hill . The canon is located at a distance of ` 800 m` from the foot to hill and can be veoved on the ground at a speed of ` 2 m//s , so that its distance from the hill can be adjusted. What is the shortest time inwhich a pachet can reach on the ground across the hill ? Taje ` g= 10 m//s^2`.
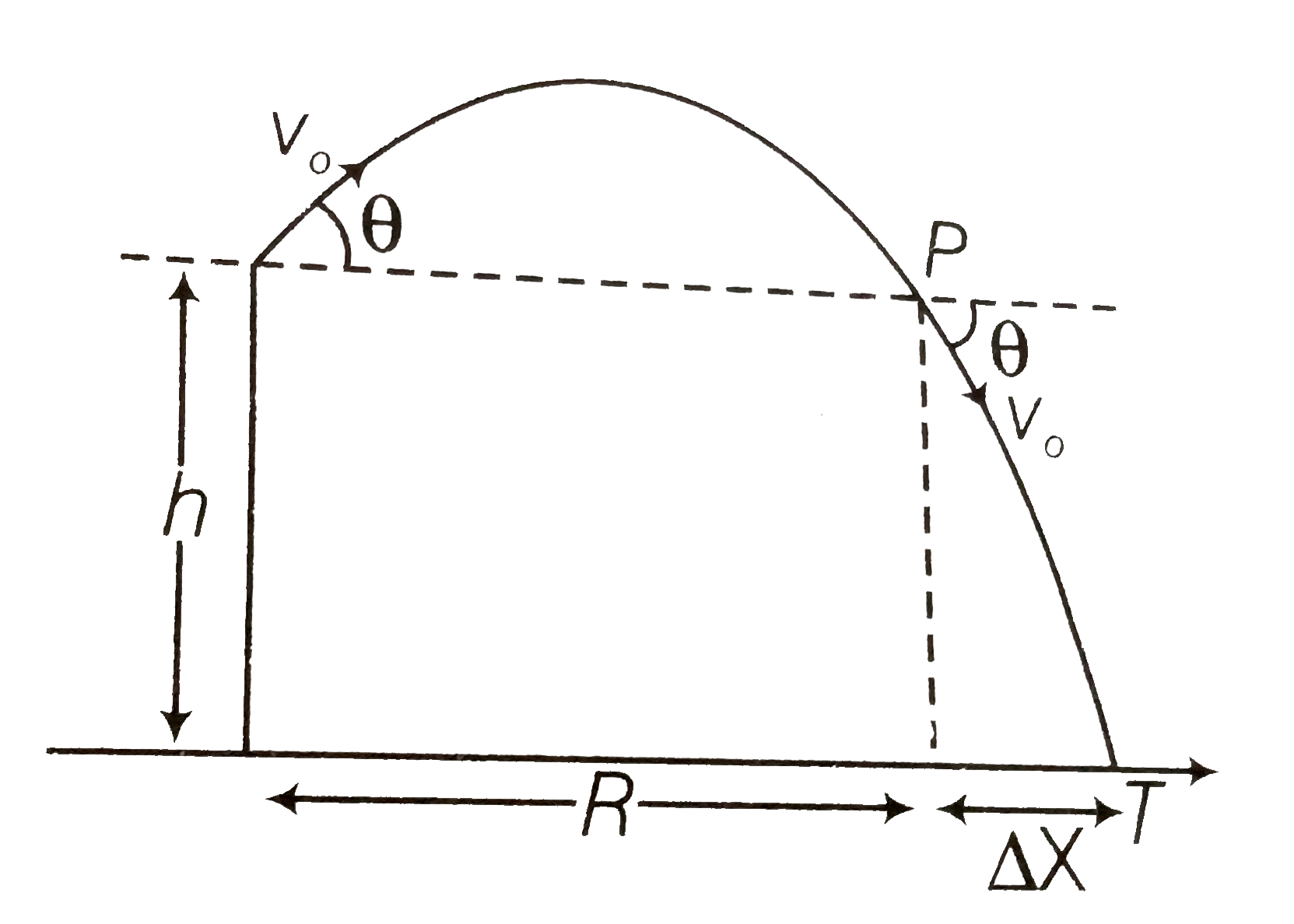
View SolutionA gun can fire shells with maximum speed `v_(0)` and the maximum horizontal range that can be achieved is `R=(v_(0)^(2))/(g)`. If a target farther away by distance `Deltax` (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least `h=Delta x[1+(Deltax)/(R)]`
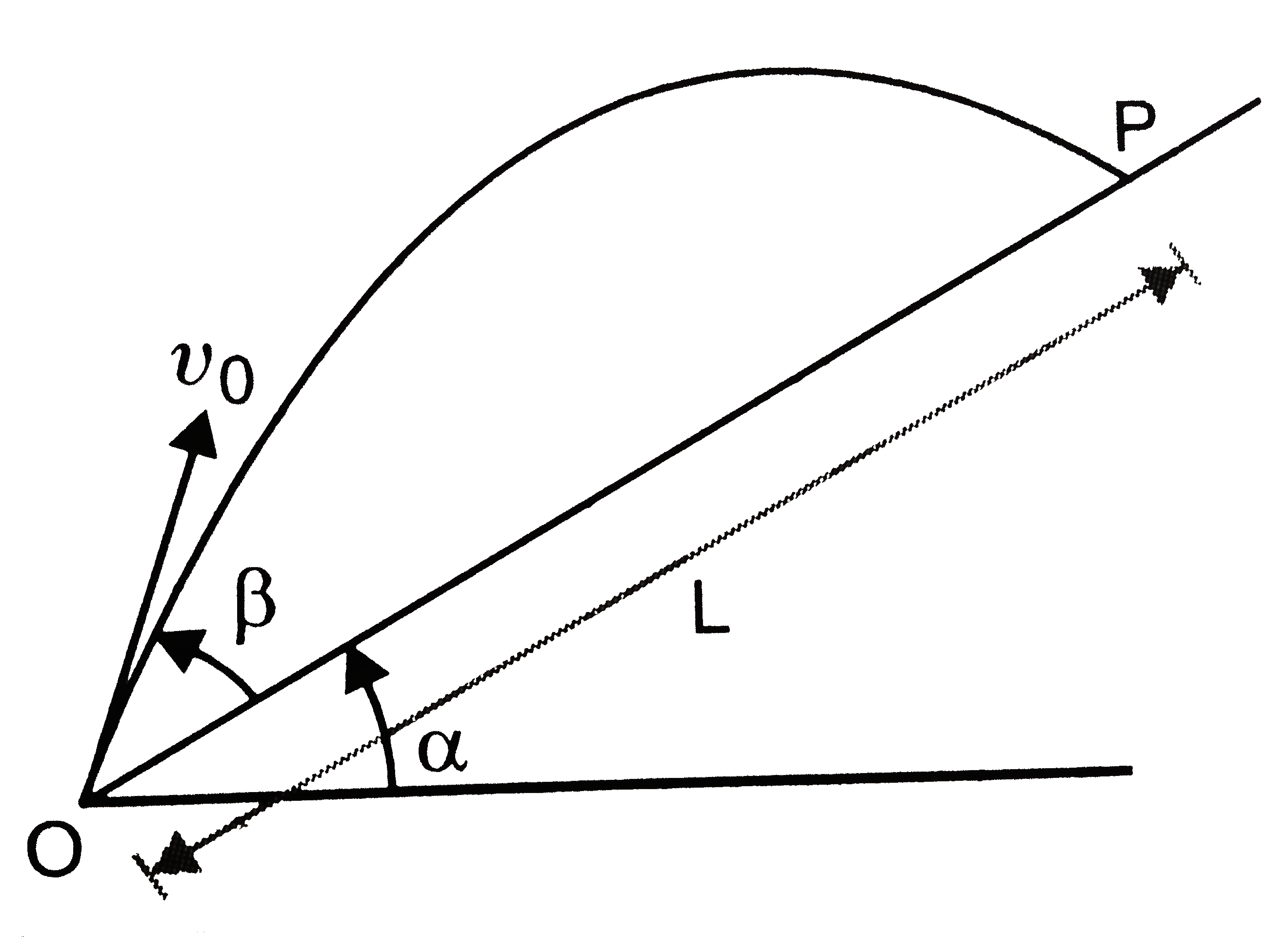
View SolutionA particle is projected in aer an angle ` beta` to a surface which itself is inclined at an angle ` alpha` to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) ` beta` at which range will be maximum.
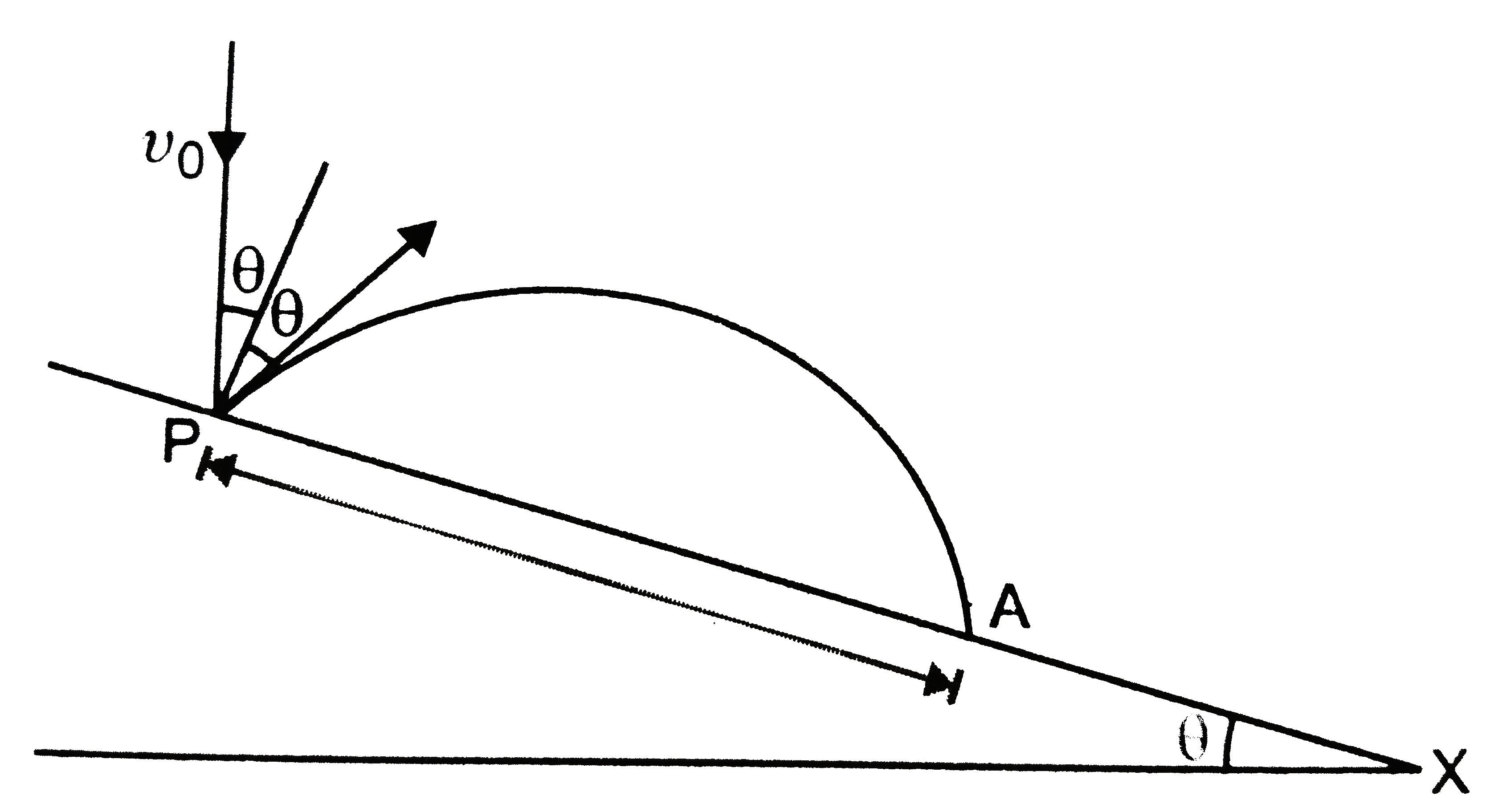
View SolutionA particle falling vertically from a height hits a plane surface inclined to horizontal at an ange ` theta` with speed ` v_0` and rebounds elastically (Fig. 2 (RP). 28). Find the distance aling the plane where it will hit second time.
 .
.
View SolutionA girl riding a bicycle with a speed of ` 5 m//s` to wards Noth direction, observes rain falling vertically down. If she increases her speed to `10 m//s`, rain appeard to meet her at ` 45^@` to the vertical . What is the speed ot the rain ? In what direction does rain fall as observed by a ground based observer ?
View SolutionA river is flowing due east with a speed ` 3 m//s` (Fig. 2 (EP) .31 ).
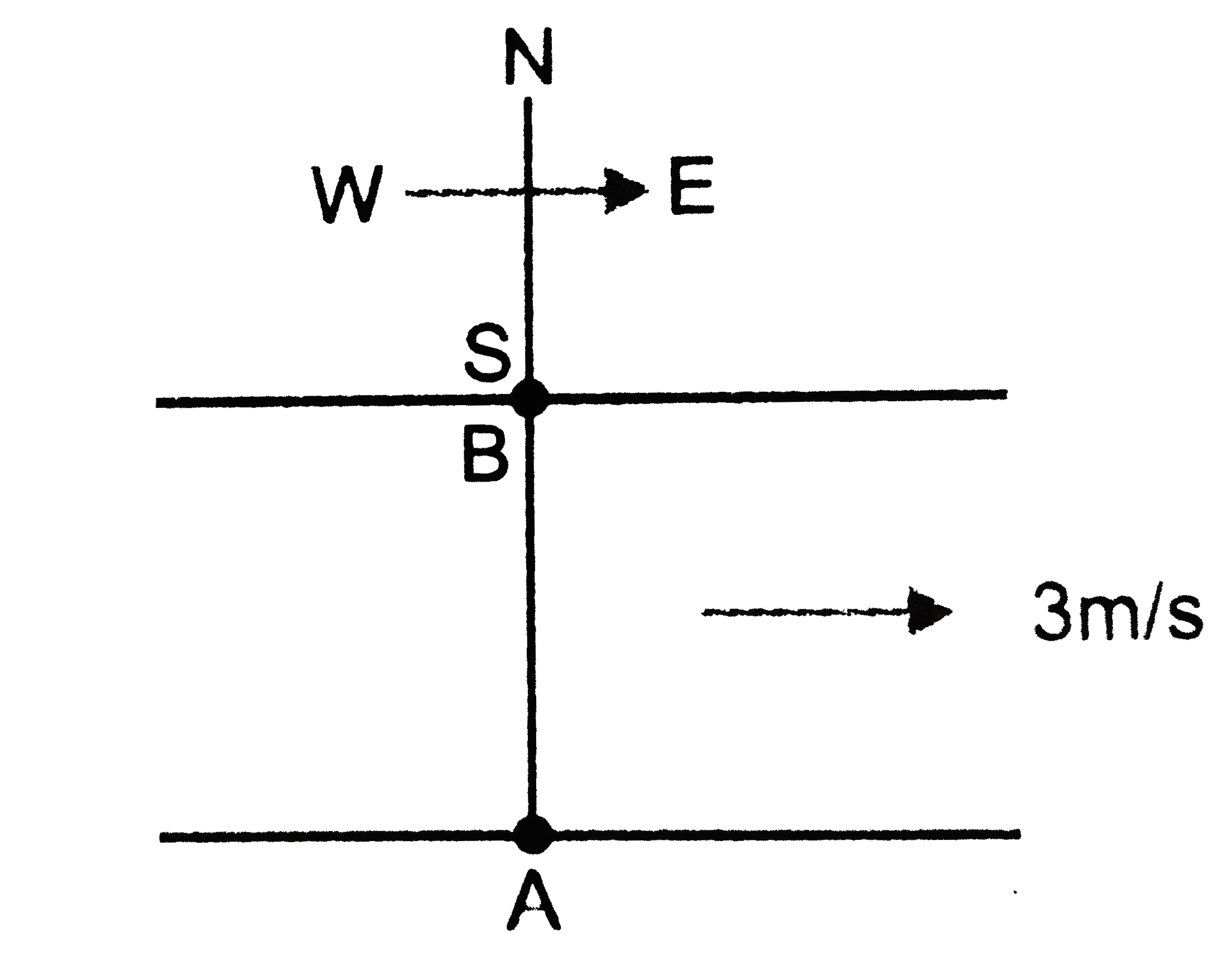 . (a) If swimmer starts swimming due borth, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
. (a) If swimmer starts swimming due borth, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
(i) Which direction should he swim? (ii) What will be his resultant speed ? (c ) From two differenrent casses as mentioned in (a) and 9b) above, in which casse will he reach opposite bank in shorter time ?
View SolutionA cricket fielder can throw the cricket ball with a speed ` v_0`. If he throws the ball while running with speed (u) at angle ` theta` to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find ` theta` at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does ` theta` for maximum range change if ` u gt v_0, u=v_0, ult v_0` ?
(f) how does ` theta` in (e) compare with that for ` u=0 (i.e., 45^@) ?
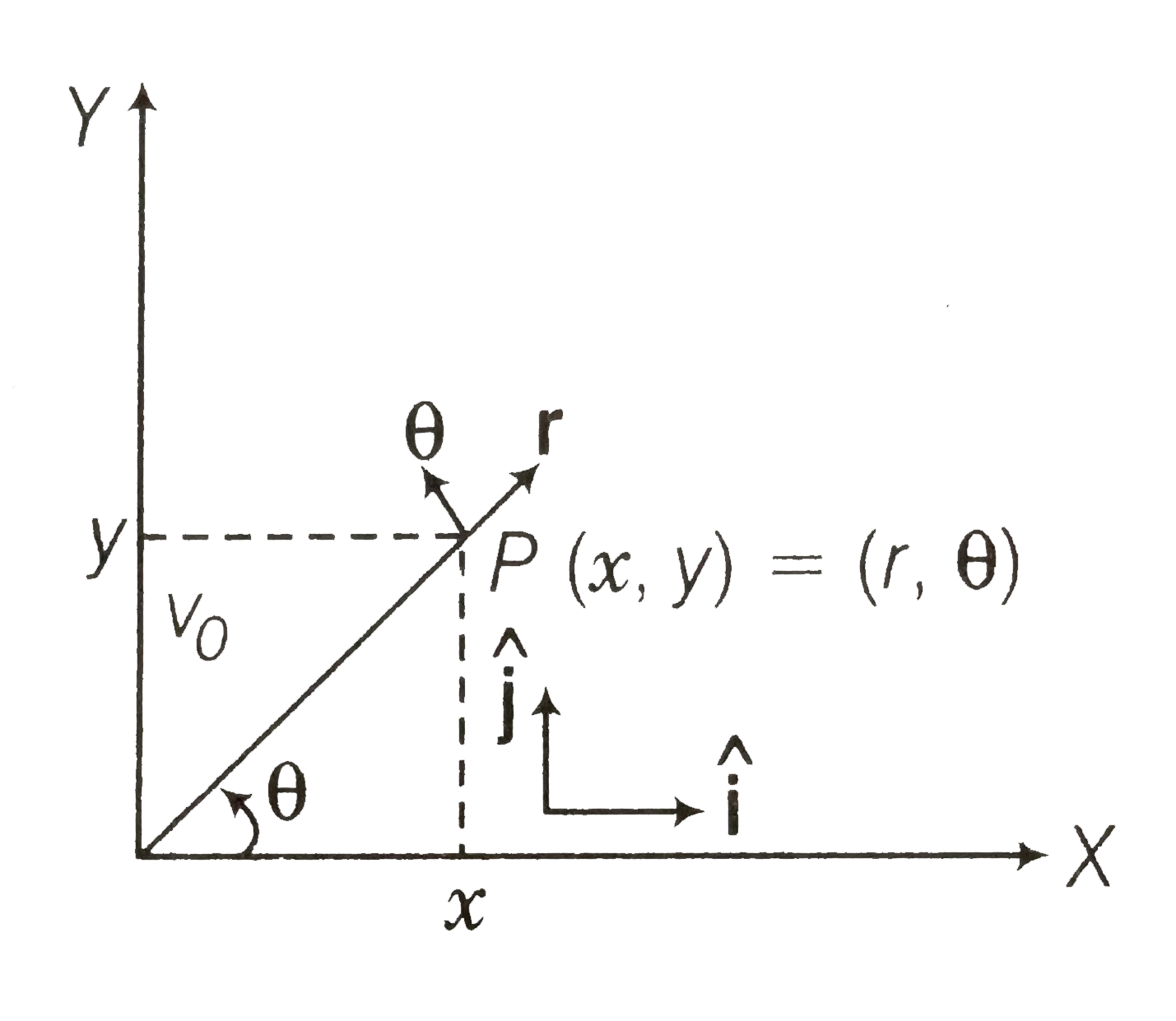
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates `A=A_(x)hat(i) + A_(y)hat(j)`, where `hat(i)` and `hat(j)` are unit vector along x and y-directions, respectively and `A_(x)` and `A_(y)` are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as `A= A_(r)hat(r) + A_(theta) hat(theta)`, where `hat(r)=(r)/(r)=cos theta hat(i)+sin theta hat (j)` and `hat(theta)=-sin theta hat(i) + cos theta hat (j)` are unit vectors along direction in which r and `theta` are increasing.
(a) Express `hat(i)` and `hat (j) ` in terms of `hat(r) ` and `hat (theta)`.
(b) Show that both `hat(r)` and `hat(theta)` are unit vectors and are perpendicular to each other.
(c) Show that `(d)/(dt)(hat(r))= omega hat(theta)`, where `omega=(d theta)/(dt)` and `(d)/(dt) (hat(theta))=-thetahat(r)`.
(d) For a particle moving along a spiral given by `r=a theta hat(r)`, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View SolutionA man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of `50mxx50m` is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s `(v lt 1)`. What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?
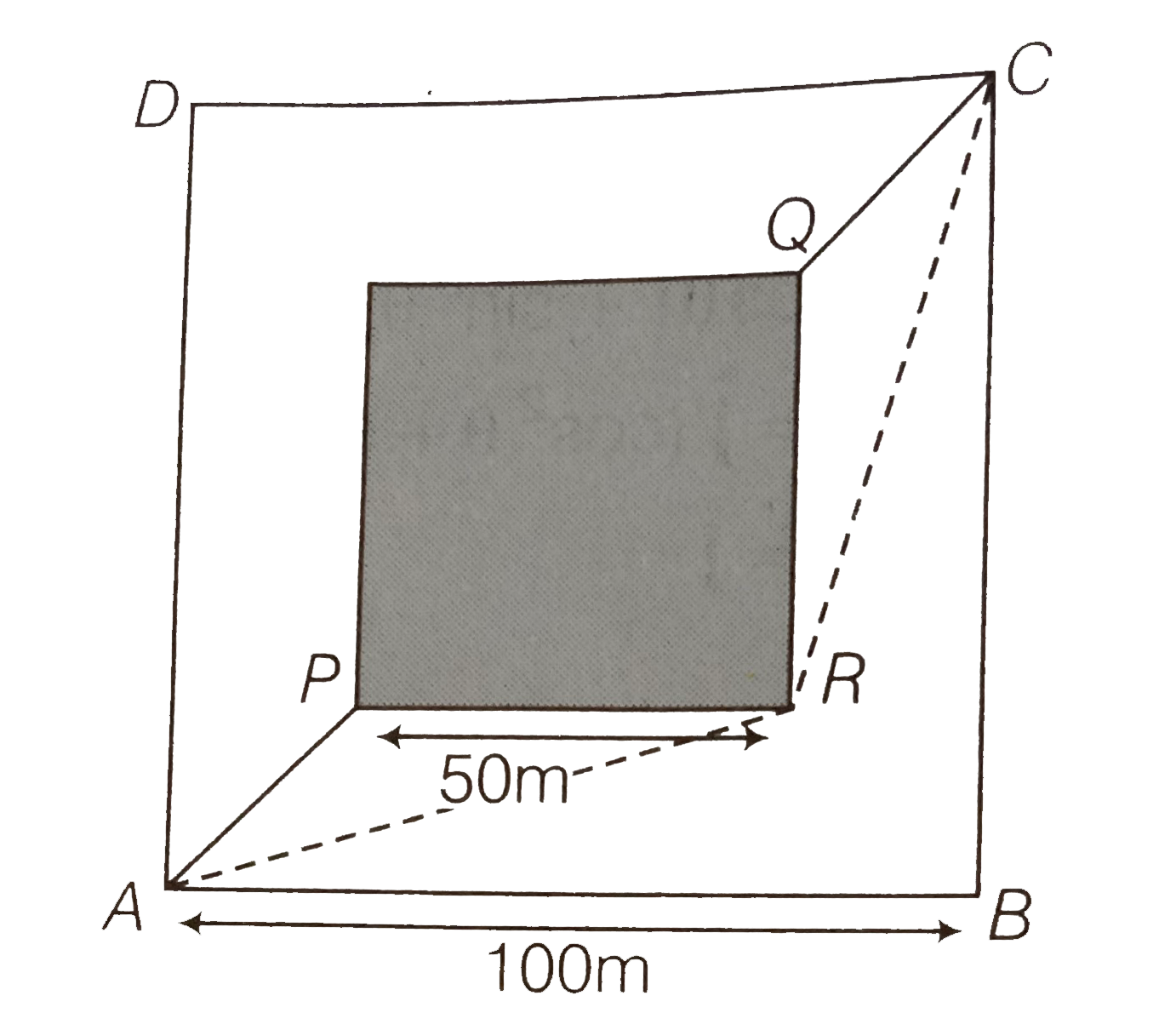
View Solution
6 Long answer (NCERT) questions and complete solutions for chapter KINEMATICS of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS KINEMATICS
- 1 Problems for practice
- 1 Con ceptual Problems
- 1 Conceptual Problems
- 1 Fill in the blanks
- 1 Long answer
- 1 Multiple choice
- 1 NCERT Assertion-Reaseon Type
- 1 NCERT Comprehension
- 1 NCERT multiple
- 1 Short answer
- 1 SolvedExamples
- 1 Very short
- 2 Con ceptual Problems
- 2 Fill in the blanks
- 2 Long answer
- 2 Multiple choice
- 2 NCERT multiple
- 2 Problems for practice
- 2 Short answer
- 2 SolvedExamples
- 2 Very short
- 3 Con ceptual Problems
- 3 Fill in the blanks
- 3 Long answer
- 3 Multiple choice
- 3 NCERT multiple
- 3 Problems for practice
- 3 Short answer
- 3 SolvedExamples
- 3 Very short
- 4 Con ceptual Problems
- 4 Conceptual Problems
- 4 Fill in the blanks
- 4 Long answer
- 4 Multiple choice
- 4 NCERT Integer type
- 4 NCERT multiple Choice
- 4 Problems for practice
- 4 Short answer
- 4 SolvedExamples
- 4 Very short
- 5 Long answer (NCERT)
- 5 Short answer
- 5 Very short
- 6 Long answer (NCERT)
- 6 Short answer
- 6 Very short
- Additional Exercises
- Advanced Problems
- Higher order thinking skills
- Motion
- NCRT Exercises
- Sample Promlem
- Value based