Complete Solutions to Advanced Problems of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PRADEEP | Advanced Problems |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
The displacement to particle is zero at ` t=0 and is z at t= t`. It starts moving in the positive x-direction with a velocity which varies, `v= k sqrt x`, wher (k) is a constant. Find the relation for variation of velocity with time.
View SolutionA bullet loses ` 1//2th1 of its velocity is passing through a plank. What is the least number of planks required to stop the bullet ?
View SolutionA balloon is ascending vertically with an acceelration of `0.2 ms^(-2)` .Two stones are dropped from it at an interval fo `2 s`, the distance between then when the second stone dropped is (tanke g=9.i8 ma^(-2).
View SolutionIf body travels half of its path in the last second of its fall from rest, find the time and height of its fall.
View SolutionA particle is moving in a plane with velocity `vec(v) = u_(0)hat(i) + k omega cos omega t hat(j)`. If the particle is at origin at `t = 0`, (a) determine the trajectory of the particle. (b) Find its distance from the origin at `t = 3pi//2 omega`.
View SolutionTwo masses ` A and B` are moving in the same straight (A) moves with a uniform vlocity 11 ms^(-1)`. (B) starts from rest at the instant it is ` 52.5 m` ahead of (A) , and moves with a uniform acceleation ` 1 ms^(-2)`. When will ` A catch B`? Explain the double answer....
View SolutionA proint moving in a straight line travels in its second, ` 16 m, 28 m and 52 m` respectively , prove that point is moving with constant acceleration. Aso find the total distance moving by particle in ` 10 seconds.
View SolutionTwo trains are headed towaads each other on the same straight rrach, each vaving a speed of ` 30 km h^(-1)`. A bird that can fly at ` 60 km h^(-1)` flies off one train when they are ` 60 km` apart and leads firectly form the otjer train, On reaching the other train, tg flies back to the first train and so on.
(a) How many trips can the bird make from one trin to the other train befre they meet ? (b) What is the total distance the bird travels ?
View SolutionTwo cars are moving in the same direction with the same speed `30 km//hr`. They are separated by a distance of `5 km`, the speed of a car moving in the opposite direction of it meets these two cars at an interval of `4` minutes, will be.
View SolutionA sports car is passing a police check post at ` 60 km h^(-1)` , immediately started slowing down uniformly until its speed was ` 40 km h^(-1)`. It continued to move at the same speed until it was passed by a police car ` 1 km` from the check post. The police car had started from rest at the check post at the same instant as the sports car had passed the check post. The police car had moved with a constant acceleraation until it had passed sports car. Assuming that the time taken by the sports car in slowing down from `60 km h^(-1)` to ` 40 km h^(-1)` was equal to the time that it travelled at constant speed before passed by the police car, find
(a) the time taken by the police car to reach the sports car
(b) the speed of the police car at the instant when it passed the sports car
(c ) the time measured from the check post when the speeds of the two cars were equal.
View SolutionThe retardation fo a moving particle if the relation between time and position is ` t= A x^3 + Bx^2 ` where ` A` and ` B` are appropriate constants will be .
View SolutionA particle moving along the x-axis has a pasition given by ` x= 10 t e^(-1)` metres where (t) is in seconds . How for is the partile from the origin when it momentarily stops ? (Do no consider its stop at infinity ).
View SolutionA person travelling east wards at the rate of ` 4 km h^(-1)` finds that the wind seems to blow directl from the borth . On dubling ins speed, the wind appears to come from ` 45^@` north of west. Find the actual velocity of the wind.
View SolutionA man running on the horizontal road at ` 8 km h^(-1)` find the rain appears to be falling vertically. He incresases his speed to `12 km h^(-1)` and find that the drops make angle ` 30^2` with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionA bird moves with velocity `20m s^(-1)` in a direction making an angle of `60^(@)` with vertical upward .Represent the velocity vector in a rectangular form.
View SolutionA smooth hemispherical bowl ` 30 cm` diameter, rotates with a constant angular velocity ` omega`, about its vertical axis of symmetry Fig. 2 (APC) . 2 (a) . A particle at (P) of weighing ` 5 kg` is observed to remain at rest relative to the bowl at a height `10 cm` above the base. Find the magnitude of the force exerted by the bowl on the particle and speed of rotation of the bowl.
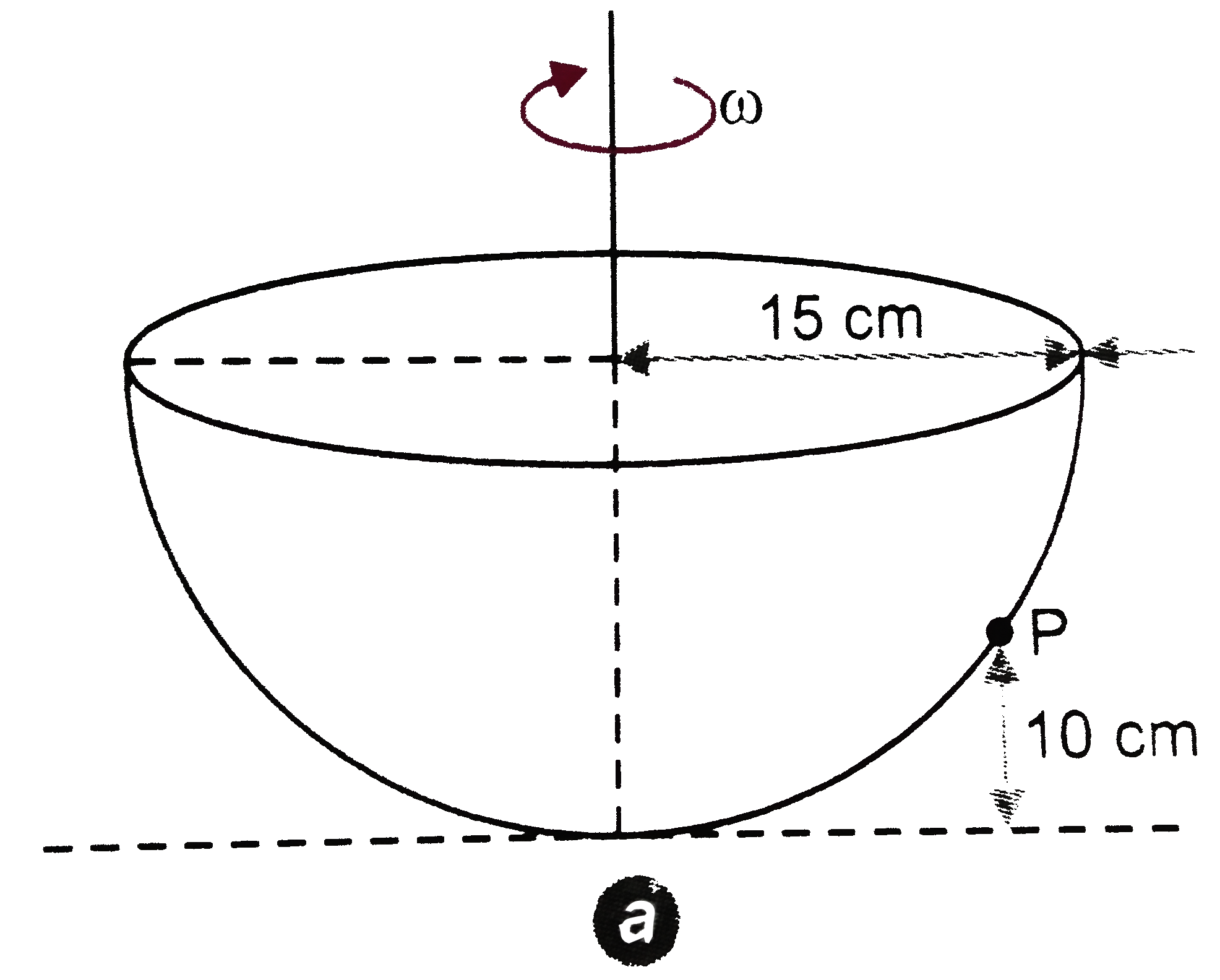 .
.
View SolutionA body is projected with a veocity of `40 ms^(-1)`. After `2 s` it fcrosses a vertical pole of height ` 20 .4 m` Find the angle of projection and horizontal range of projectile. (g = 9.8 ms^(-2)`.
View SolutionTwo inclined planes (AB) and (BC) are placed as shown in Fig. 2 (ABC).3 A particle is projected from the foot of the plane of angle ` alpha` along its line witn a velocity just sufficient to carry it to the top after which the particle slides down the other inclined plane. Fing the total time it will take to reach the pont (C ).
View SolutionIf the horizontal range of projectile be (a) and the maximum height attained by it is (b) then prove that the velocity of projection is
` [ 2 g (b+ a^2 /(16 b)) ] ^(1//2)`.
View SolutionAn object `A` is kept fixed at the point ` x= 3 m` and `y = 1.25 m` on a plank `p` raised above the ground . At time ` t = 0 ` the plank starts moving along the `+x` direction with an acceleration ` 1.5 m//s^(2) `. At the same instant a stone is projected from the origin with a velocity `vec(u)` as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle ` 45(@)` to the horizontal . All the motions are in the ` X -Y `plane . Find ` vec(u)` and the time after which the stone hits the object . Take ` g = 10 m//s`
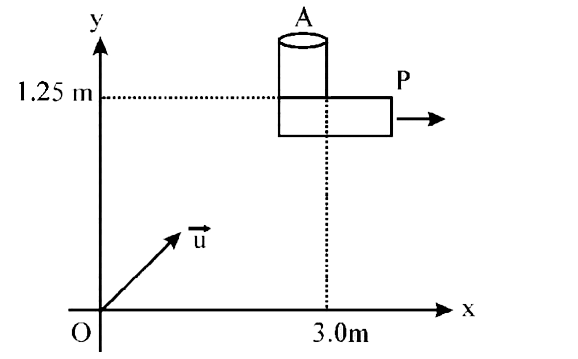
View Solution
Advanced Problems questions and complete solutions for chapter KINEMATICS of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS KINEMATICS
- 1 Problems for practice
- 1 Con ceptual Problems
- 1 Conceptual Problems
- 1 Fill in the blanks
- 1 Long answer
- 1 Multiple choice
- 1 NCERT Assertion-Reaseon Type
- 1 NCERT Comprehension
- 1 NCERT multiple
- 1 Short answer
- 1 SolvedExamples
- 1 Very short
- 2 Con ceptual Problems
- 2 Fill in the blanks
- 2 Long answer
- 2 Multiple choice
- 2 NCERT multiple
- 2 Problems for practice
- 2 Short answer
- 2 SolvedExamples
- 2 Very short
- 3 Con ceptual Problems
- 3 Fill in the blanks
- 3 Long answer
- 3 Multiple choice
- 3 NCERT multiple
- 3 Problems for practice
- 3 Short answer
- 3 SolvedExamples
- 3 Very short
- 4 Con ceptual Problems
- 4 Conceptual Problems
- 4 Fill in the blanks
- 4 Long answer
- 4 Multiple choice
- 4 NCERT Integer type
- 4 NCERT multiple Choice
- 4 Problems for practice
- 4 Short answer
- 4 SolvedExamples
- 4 Very short
- 5 Long answer (NCERT)
- 5 Short answer
- 5 Very short
- 6 Long answer (NCERT)
- 6 Short answer
- 6 Very short
- Additional Exercises
- Advanced Problems
- Higher order thinking skills
- Motion
- NCRT Exercises
- Sample Promlem
- Value based