Complete Solutions to 2 SolvedExamples of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PRADEEP | 2 SolvedExamples |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
A car moving along a straight highway with a speed of `72 km h^(-1)` is brought to a stop within the distance of `100 m`. What is the retardation of the car and how long does it take for the car to stop ?
View SolutionA body covers `10 m` in 4 second and ` 15m` in 16 second of its uniformly accelerated motion. How far will it travel in the next 3 seconds?
View SolutionA ball is thrown vertically upwards with a velcotiy of `20 ms^(-1)` from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25-0m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. `g=10 ms^(-2)`.
View SolutionA driver of car takes `-20 s` (which is the reaction time of dricer ) to apply the brkes after he sees an obstruction at a distance of `25 m` from him . If he is driving car at a speed of `54 km h^(-1)` and the brakes cause a deceleration of `6.0 km h^(-2), predict whether he will avert collistion or not.
View SolutionOn a foggy day, the two cars are approaching each other on a straight road, with speeds `72 km h^(-10` and `54 km h^(-1)`. The drivers of the cars spot other when they were `60` meres apart. Both of them applied brakes, retarding their cars at of `6 ms^(-1)`. Predict whether they will avert collision or not.
View SolutionA body travels a distance of `2 m` in `2` seconds and `2.2m` next `4 seconds`. What will be the velocity of the body at the end of `7` the second from the start?
View SolutionA motor car starts from rest and accelerates uniformly for `10 s` to a velocity of `30 ms^(-1)`. It then runs at a constant speed and is finally brought to distance covered is `830 m`. Find the value of acceleration, retardation and total time taken.
View SolutionA man `16 m` behind the door of a train when it starts it starts moving with an acceleration `a=2 ms^(-1)`.The man runs with a msximum constant speed to get into the train. How for does he have to run and after what time does he get the train ? What is his maximum constant speed ?
View SolutionTwo buses `A and B` are at positions `60 m` 160 m` from the origin at time `t=0`. They start moving in the same direction simultaneously with uniform speed `54 km h^(-1)` and `36 km h^(-`)`. Derermine the time and positiona t which `A overtaken B`.
View SolutionProve that the distances traversed during equal intervals of time by a body falling from rest, stand to one another in the same fatio as the odd mumbers beginning with unity [namely 1: 3: 5: …………….].
View SolutionForm the top of a tower `100 m` in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of `25 ms^(-1)`. Find when and where the two balls will meet.
View SolutionA tennis ball is dropped on to the floor from a height of `4.00 m`. It rebounds to a height of `3.00 m`. If the ball was in contact with the floor for `0.010 sec`, what was its average acceleration during contact?
View SolutionA parrachutist bails out from an aeropane and after dropping through a distance of `40 m` opens the parachute and decelerates at `2 ms^(-2)`. If he reaches the ground with a speed of `2 ms^(-1)`, how lowg he in the air ? At what height did he bail out from the plane ?
View SolutionA body is dropped from rest at a height of `150 m` and simultanceously, another body is dropped from rest from a point `100 m` above the ground. What is the difference between heights after theymave fallen for (i) `3s (ii) 5s`. Consider that the body on reaching fround remains there and acceleration due to gravity be `10 m//s^(2)`.
View SolutionA balloon starts rising from the ground with an acceleration `2 ms^(-2)`. After `5 second , a stone is released from the ballooon. Find the time taken by the stone to reach the ground after its release and total height attained by ballooon when stone reaches the ground. Take `g==10 ms^(-2)`.
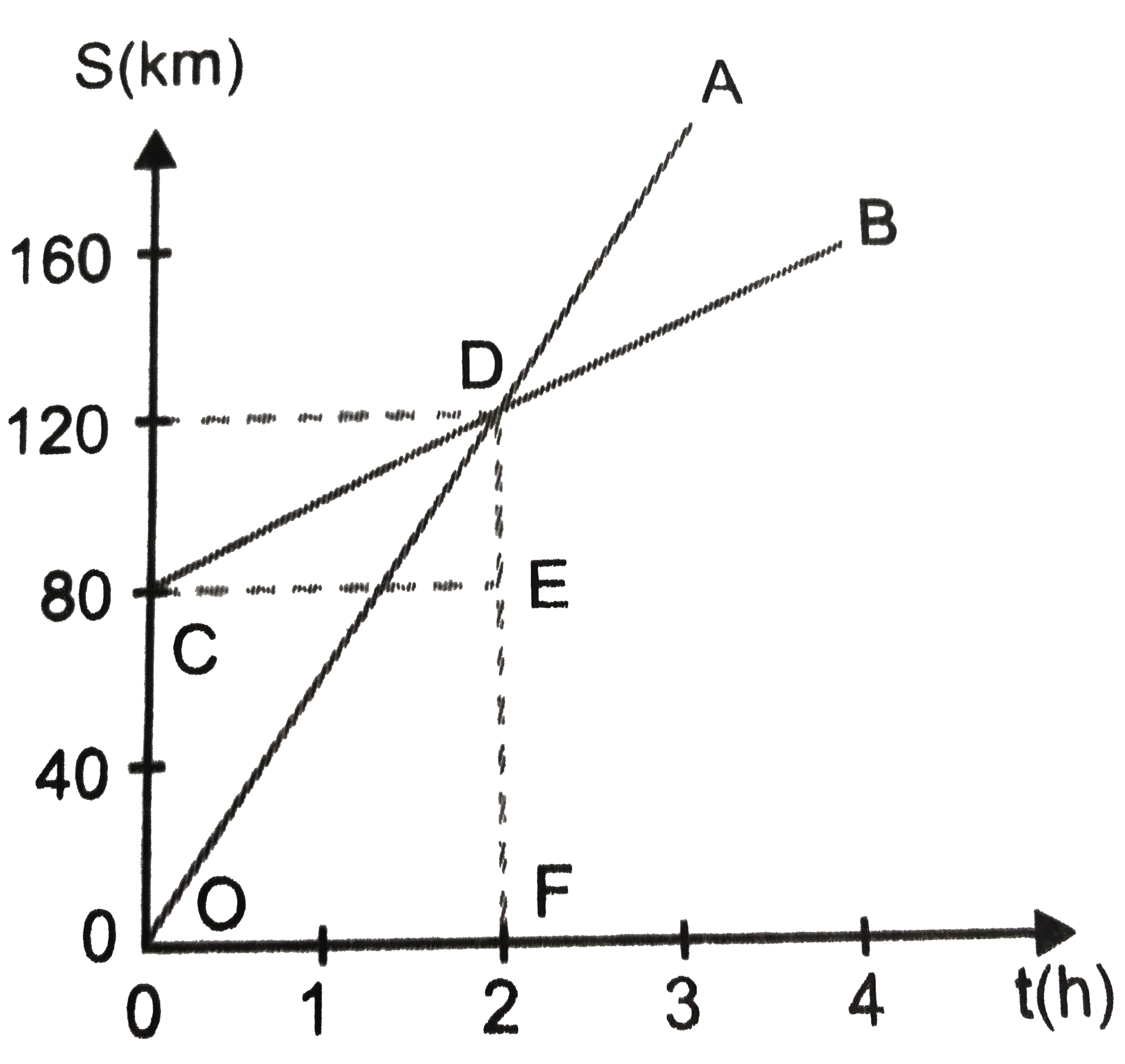
View SolutionFig. 2 (b). 12` shows thae distance (S) -time (t) graphs of two trains, which start moving simultaneously in the same direetion. From the graphs, find:
 .
.
(a) How much (B) is ahead of (A) when motion starts
(b) What is the speed of (B) ?
( c) What and where (A) will catch (B) ? `
(d) What is the differnce in speeds of (A) and (B) ? lt
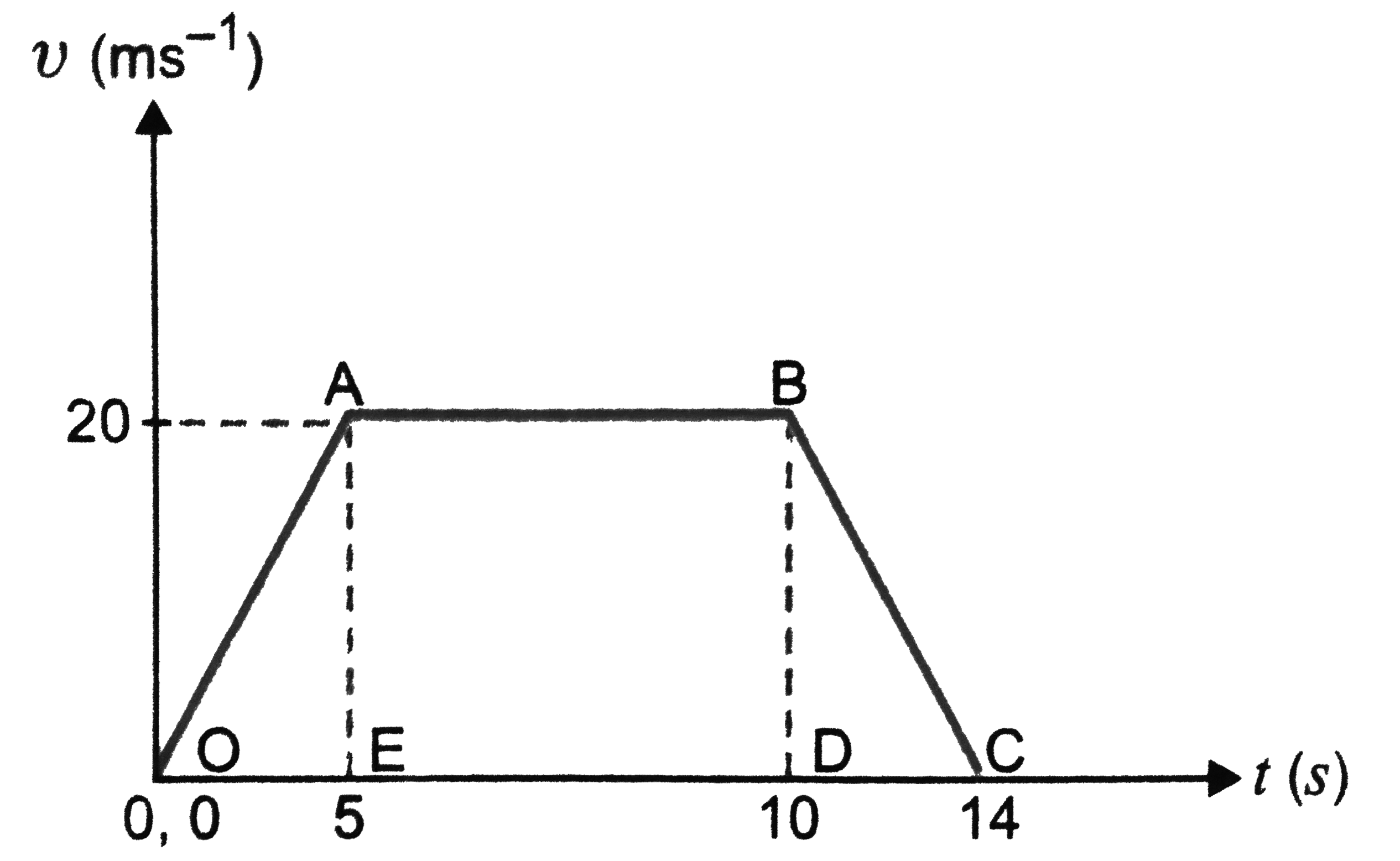
View SolutionVelocity (v) time (t) graph of a car starting from rest is shown in Fig. 2(b). 13. Draw acceleration (a) -time (t) graph for the motion of the car and find total distance travelled by car.
 .
.
View SolutionA body starting from rest acclerates uniformly along a st. line , at the rate of `10 ms^(-2)` for 5 s`. It moves for `2 s` with uniform velocoty of `50 ms^(-1)`. The it retards uniformly and comes to rest in 3 s`. Draw velocity-time graph of the and find the total distance travelled by body.
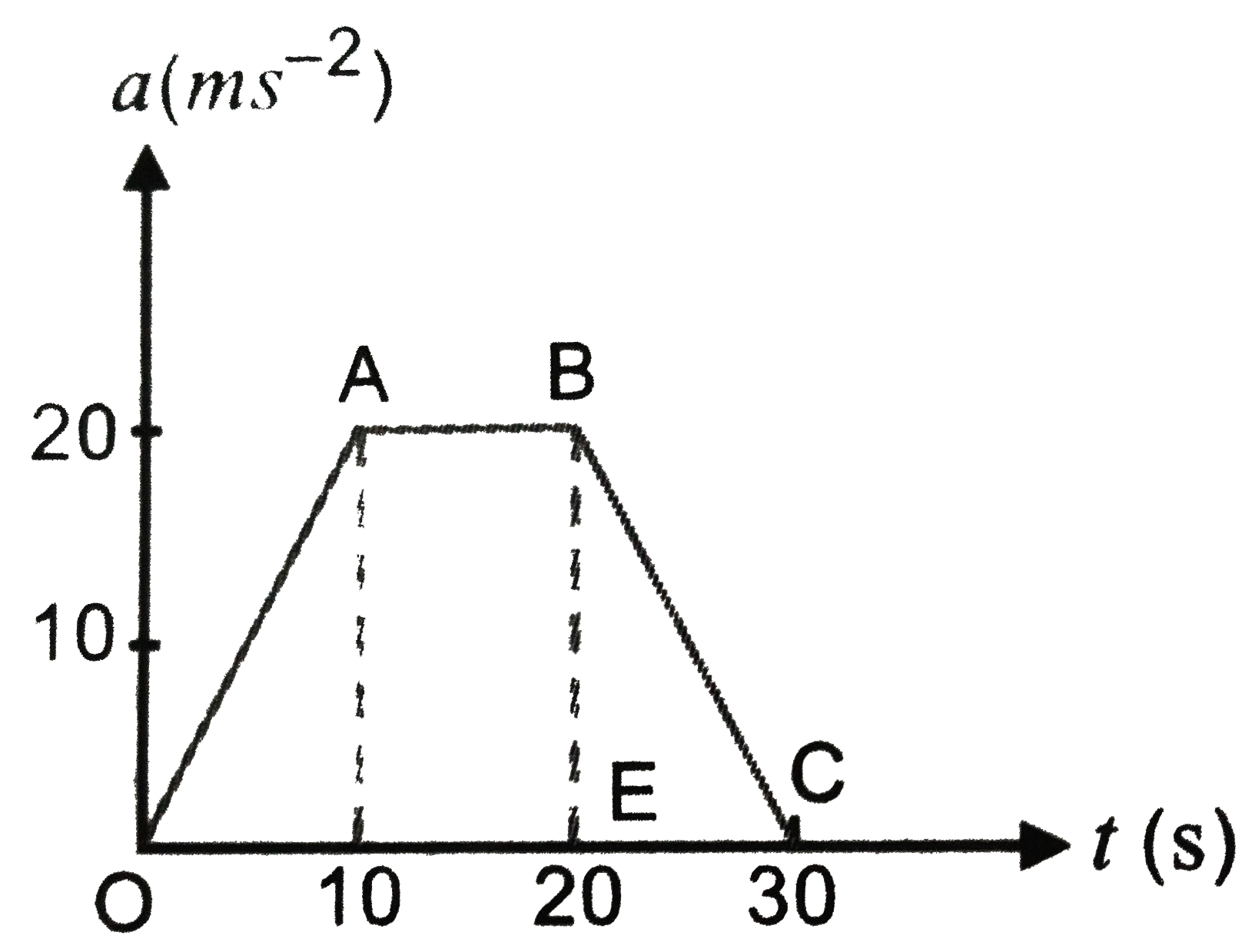
View SolutionFig. 2 (b) .16 shows the time-acceleration graph for a particle in rectillinear motion. Find the averate acceleration in first twenty seconds.
 .
.
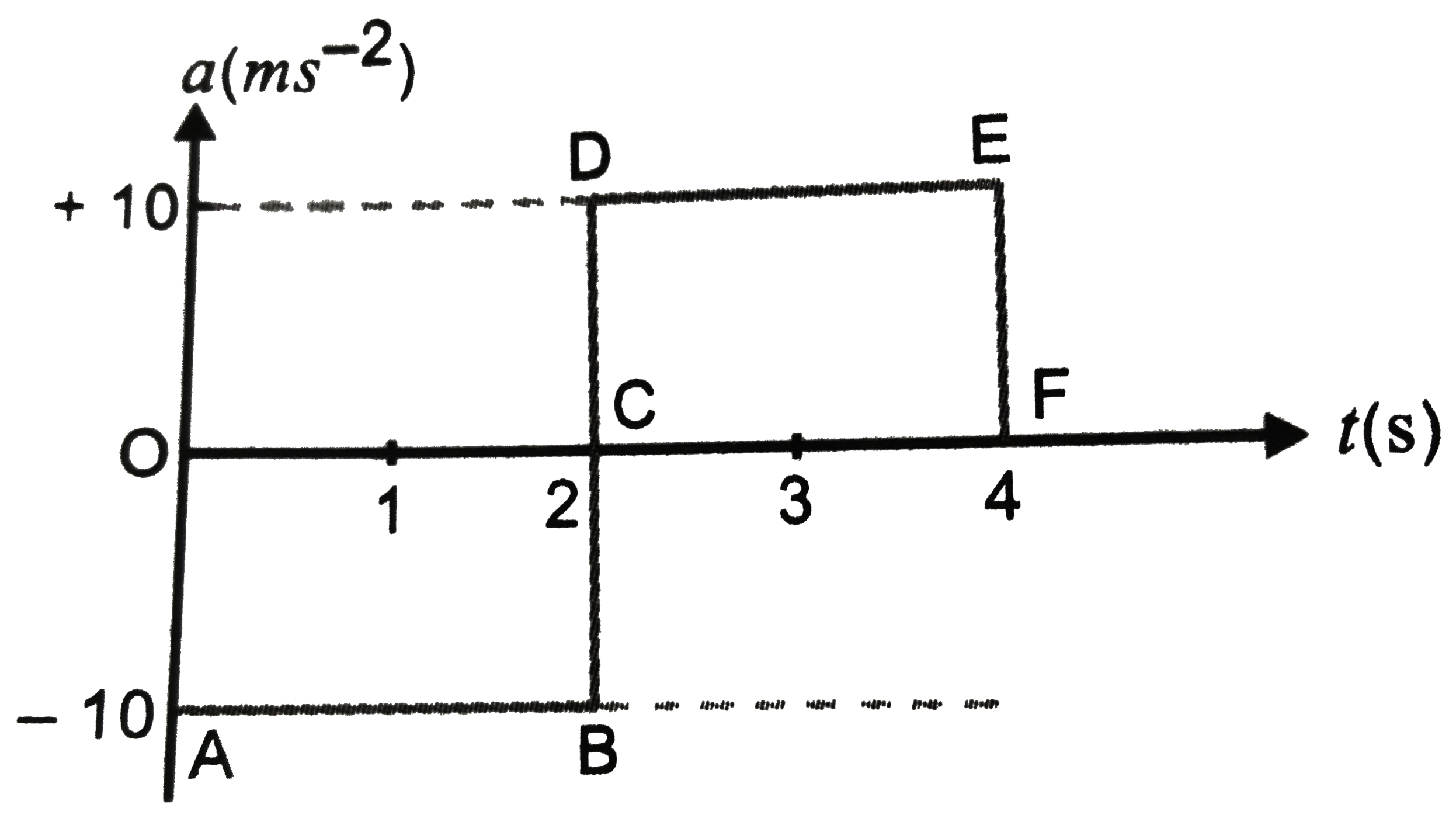
View SolutionA particle starts from rest at time `t=0` and moves on a straight line with acceleration a (ms^-2) as plotted in Fig. 2 (b) .17. Find the time at which the speed og the particle is maximum. Also calculate the displacement of theparticle from starting point after `4 s`.
 .
.
View SolutionA ball is thrown upward with an initial velocity of `80 ms^(-1)`. After how much time will it return to ground ? Draw velocity-time graph for the ball and find from the graph
(a) the maximum height attained by ball and
(b) height of the ball after `12 s`. Take `g=10 ms^(-2)`.
View SolutionThe distance travelled by a particle moving along a st. line is given by `x=4 t + 5t^(2) +6^(3)` mette.
Find (i) the initial velcity of the particle (ii) the velcoty at the end of `4 s` and (iii) the acceleration of the particle at the end of `5 second.
View SolutionThe velocity of a particle is given by `v=u_(0) + g t+ 1/2 at^(2)`. If its position is `x =0` at `t=0`, then what is its displacement after `t=1 s` ?
View SolutionThe position of an object moving along x-axis is given by `x = a + bt^2` where `a=8.5 m, b=2.5 m s^-2 and t` is measured in seconds. What is its velocity at `t= 0 s and t = 2.0 s`. What is the average velocity between `t = 2.0 s and t = 4.0 s?`
View SolutionThe distance (x) particle moving in one dismension, under the action of a constant force is related to time (t) by equation `tsqrt x +3`
where (x) is in vettres and (t) in seconds. Find the displacement of the particle when its velcity is zero.
View SolutionAn object , moving with a speed of ` 6.25 m//s `, is decelerated at a rate given by :
`(dv)/(dt) = - 2.5 sqrt (v)` where `v` is the instantaneous speed . The time taken by the object , to come to rest , would be :
View SolutionA bird flies for `4 s` with a velcoty `v=t (-2) ms^(-1) in a stralght line. Calculate the displacement of the bird ans distance travelled by the bird.
View SolutionA particle is moving in a straight line with constant acceleration. If x,y and z be the distances described by a particle during the pth, qth and rth second respectively, prove that
View SolutionA juggler throws ball into air. He throus one whenever the previus one is at its highest point. How high do the balls rise if he throus (n) balls each second. Acceleration the to gravity=g`.
View SolutionThe relation between time t and displacement x is `t = alpha x^2 + beta x,` where `alpha and beta` are constants. The retardation is
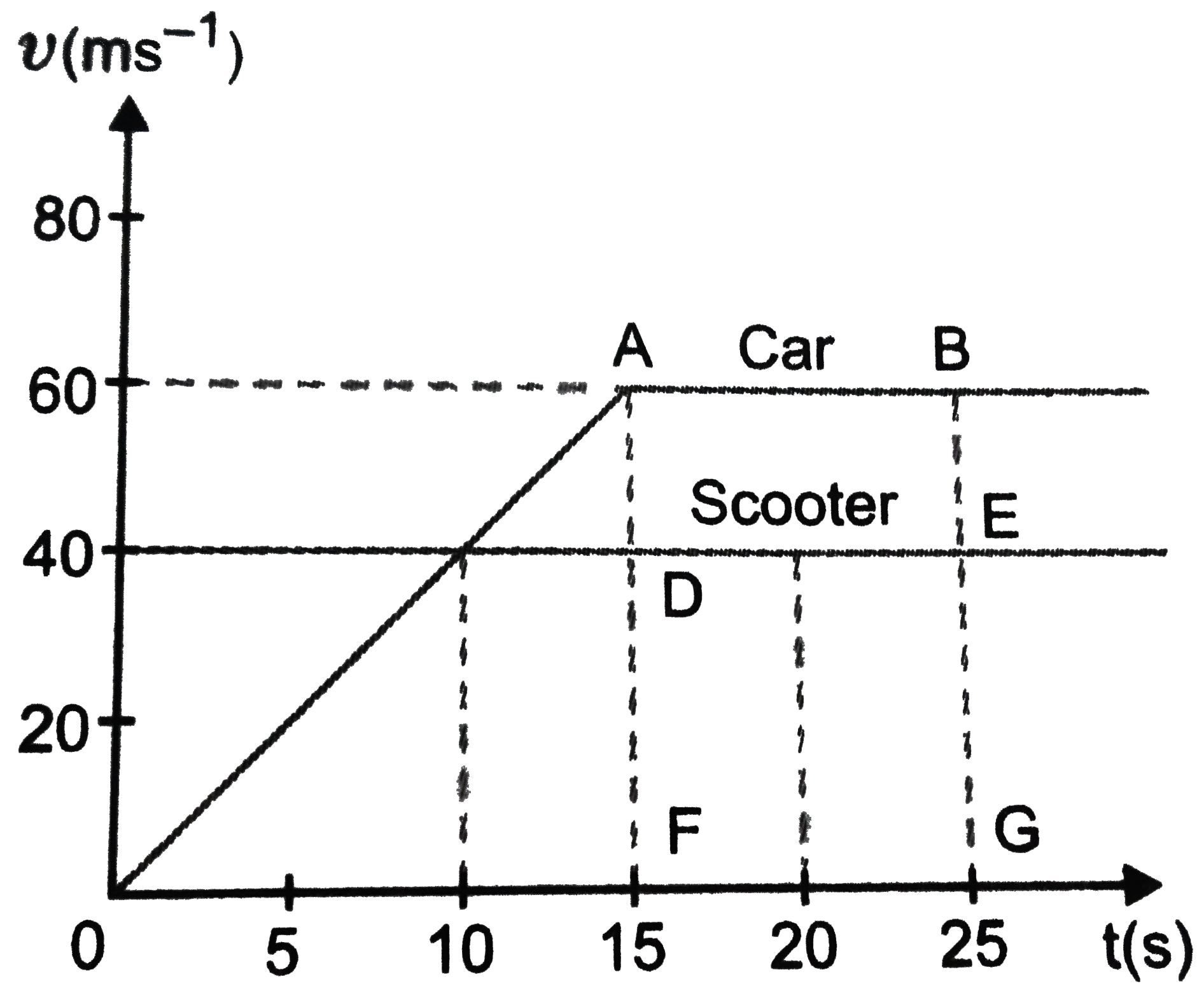
View SolutionAs soon as a car starts from rest in a certain dirction, a scooter moving with a uniform speed overtakes the car. Their velcity-time graphs are shown in Fig. 2 (b) .19.` Calcutate
(a) the difference between the distances travelled by the car and the scooter in `25 s`.
(b) the time when car will catch up the secooter.
(c ) the distance of the car and scooter from the starting point at the meeting point.
 .
.
View Solution
2 SolvedExamples questions and complete solutions for chapter KINEMATICS of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS KINEMATICS
- 1 Problems for practice
- 1 Con ceptual Problems
- 1 Conceptual Problems
- 1 Fill in the blanks
- 1 Long answer
- 1 Multiple choice
- 1 NCERT Assertion-Reaseon Type
- 1 NCERT Comprehension
- 1 NCERT multiple
- 1 Short answer
- 1 SolvedExamples
- 1 Very short
- 2 Con ceptual Problems
- 2 Fill in the blanks
- 2 Long answer
- 2 Multiple choice
- 2 NCERT multiple
- 2 Problems for practice
- 2 Short answer
- 2 SolvedExamples
- 2 Very short
- 3 Con ceptual Problems
- 3 Fill in the blanks
- 3 Long answer
- 3 Multiple choice
- 3 NCERT multiple
- 3 Problems for practice
- 3 Short answer
- 3 SolvedExamples
- 3 Very short
- 4 Con ceptual Problems
- 4 Conceptual Problems
- 4 Fill in the blanks
- 4 Long answer
- 4 Multiple choice
- 4 NCERT Integer type
- 4 NCERT multiple Choice
- 4 Problems for practice
- 4 Short answer
- 4 SolvedExamples
- 4 Very short
- 5 Long answer (NCERT)
- 5 Short answer
- 5 Very short
- 6 Long answer (NCERT)
- 6 Short answer
- 6 Very short
- Additional Exercises
- Advanced Problems
- Higher order thinking skills
- Motion
- NCRT Exercises
- Sample Promlem
- Value based