Complete Solutions to 3 NCERT multiple of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PRADEEP | 3 NCERT multiple |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A student goes from his to his friend`s house with speed ` v_1`. Finding the door of his friend`s home closed, he returns back to his own house with the speed ` v_2`. Then the averge speed and net displacement of student is [consider distance between two houses be S].
View SolutionA particle position as function of time is described as ` y (t) =5 cos (10 t + 15)` in meters. What is the average velocity of the particle from ` t=0` at ` t= 3 sec` ?
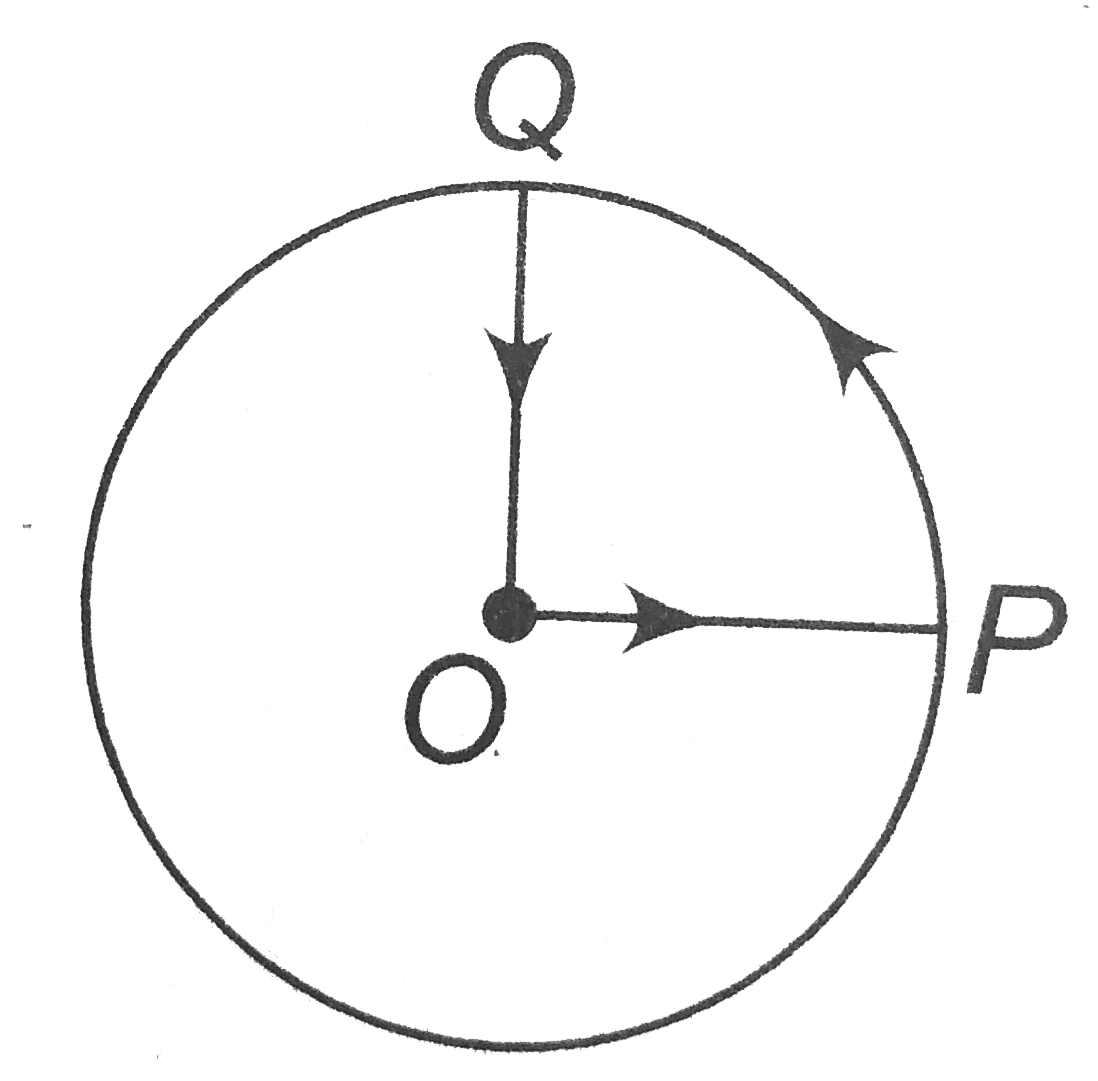
View SolutionA cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ cicumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minute, the net displacement and average speed of the cylists (in kilometer and kinetic per hour) is
View SolutionA body moves along a quadrant of a circle of radius (r). The displacement and distance traveled are.
View SolutionTwo straight lines drawn on the same displacement-time graph make angles `30^(@)` and `60^(@)` with time-axis respectively Fig. 2 (a) .36 Which line represents greater velocity? What is the ratio of two velocities?
 .
.
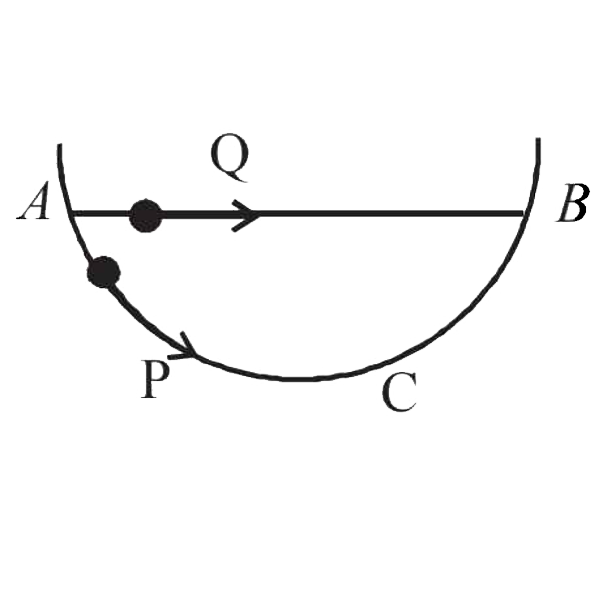
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at `t=0`. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at `t=0` along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let `t_P` and `t_Q` be the respective times taken by P and Q to reach the point B. Then:
View SolutionA body of mass (m) moving along a straight line covers half the distance with a speed of 2 m/s. The remaining half of the distance is covered in two equal tiem intervals with a speed of ` 3 ms^(-1)` and ` 5 ms^(-2)` respectively. The average speed of the particle for the entire journey is .
View SolutionA car travels half the distanace with constant velocity ` 30 km //h` and another half with a constant velocity of ` 40 km //h along a straight line. The average velocity of car in km//h is.
View SolutionA cae movies a distance of ` 200 m`. It covers the first half of the distance at speed of ` 40 km//h` and second half of the distance at a speed (v). The average speed is ` 48 km//h`. Find the value of (v) .
View SolutionA car runs at a constant speed on a circulat track of radius ` 100 m`. Taking `62.8 s` for every circular lap. The average velocity and average speed for each circular lap respectively are :
View SolutionTaxis leave station `X` for station `Y` every `10 min`. Simultaneously, a taxi also leaves station `Y` for station`X` every `10 min`. The taxis move at the same constant speed and go from `X` and `Y` or vice-versa in `2 h`, How many taxis coming from the other side will meet each taxi enroute from `Y` and `X`?.
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance `S_1` in the first 10 sec and a distance `S_2` in the next 10 sec, Then
View SolutionA man throws ball into the air one after the other. Throwing one when other is at the highest point. How high the balls rise if he throws twice a second.
View SolutionA bus begins to move with an acceleration of ` 1 ms^(-1)` . A man who is `1 48m` behind the bus starts running at ` 10 ms^(-1)` to catch the bus, the man will be able to catch the bus after .
View SolutionA particle is moving such that its position coordinates `(x, y)` are `(2m, 3m)` at time `t=0, (6m, 7m)` at time `t=2 s`, and `(13 m, 14m)` at time `t=5 s`.
Average velocity vector`(vec(V)_(av))` from `t=0` to `t=5 s` is
View SolutionAirplanes `A` and `B` are flying with constant velocity in the same vertical plane at angles `30^(@)` and `60^(@)` with respect to the horizontal respectively as shown in figure . The speed of `A` is `100sqrt(3) m//s` . At time `t = 0 s`, an observer in `A` finds `B` at a distance of `500 m`. The observer sees `B` moving with a constant velocity perpendicular to the line of motion of `A` . If at `t = t_(0)`, A just escapes being hit by `B ,t_(0)` , A just escapes being hit by `B , t_(0)` in seconds is

View SolutionTwo balls of equal masses are thrown upwards along the same vecticla direction at an interavel of ` 2 seconsds`. With the same intial velcity of ` 39.2 m//s` . The these collede at a height of .
View SolutionTwo balls of equal masses are thrown along the same vertical direction at an interval of ` 2 seconds`, with the same initial velocity of 1 45 ms^(-1)`. Then these balls collide at a height of (use g=10 ms^(-2)`
View SolutionA body dropped from top of a tower falls through ` 40 m` during the last two seconds of its fall. The height of tower in m is ( g= 10 m//s^@)`
View SolutionA body is rpojected vertically upwards with a velocity of `10m//s`. If reaches the maximum height (h) in time (t). In time ` t//2` the height covered is (g= 10 m//s^@)`
View SolutionTwo trains travelling on the same track are approaching each other with equal speed of ` 40 m//s`. The drivers of the trains beging to decelerate simultaneously when just ` 2.0 km apart. Assuming deceleration to be uniform and equal the value to the deceleration to barely avoid collision should be .
View SolutionA particle movig with a uniformacceleration travels ` 24 ` metre and ` 64` metre in first two successive intervals of ` 4` seconds each. Its initial velocity is.
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
View SolutionA body released from the top of a tower falls through half the height of tower in `3` seconds. If will reach the ground after nearly .
View SolutionA ball is thrown up, it reaches a maximum height anf then comes down. IF ` t_1` and `t_2` (t_2 gt t_1)` ar the time that the ball takes to be at a particular height then the time taken by the ball to reach the highest point is .
View SolutionA particle is dropped from rest from a large height Assume `g` to be constant throughout the motion. The time taken by it to fall through successive distance of `1 m` each will be :
View SolutionA balloon starts rising from the ground with an acceleration of `1.25ms^-2`. After 8 seconds, a stone is released from the balloon. After releasing, the stone will:
View SolutionA man in a balloon rising vertically with an accelration fo `4.9 ms^(-2)` released a ball `2 seconds` after the balloon is let fo from the fround. The greatst height above the ground reached by the ball is .
View SolutionA bullet loses ` 1//20` of its velocity in passing through a plank. What is the least number of plank required to stop the bullet .
View SolutionA balloon rises from rest on the ground with constant acceleration `g`//`8.` A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA ball rleased from the tope of a tower travels ` (11) /( 36) ` of the height of the tower in the last second of its journey. The height of the tower is (g= 10 ms^(2)).
View SolutionIf a particle is thrown vertically upwards , then its velocity so that it covers same distance in ` 5th and 6th seconds would be .
View SolutionA car acceleartion from reat at a constant rate of ` 3ms^(-2) for sometime. Then it retards at constant tate of 6 ms^(-1)` and comes to rest. If the total tiem for which it remains in motion is ` 3` seconds. What is the total distance travelled ?
View SolutionA stone is dropped from a certain height which can reach the ground in `5 s`. It is stopped after `3 s` of its fall and then it is again released. The total time taken by the stone to reach the ground will be .
View SolutionThe ball is dropped from a bridge ` 122.5 m` above a river, After the ball has been falling for 2 s, a second ball is thrown straight down after it. What must its initial velocity be so that both hit the water at the same time ?
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time `t` is proptional to
View SolutionA particle is moving in a straight line with initial velocity `u` and uniform acceleration `f`. If the sum of the distances travelled in `t^(th) and (t + 1)^(th)` seconds is `100 cm`, then its velocity after `t` seconds, in `cm//s`, is.
View SolutionTwo particles , one with constant velocity ` 50 m//s` and the other with uniform acceleration ` 10 m//s^(-2)`. Start moving simultaneously from the same place in the same direction. They will be at a distance of `125m` other after.
View SolutionA ball is dropped vertically from `a` height `d` above the ground . It hits the ground and bounces up vertically to a height ` (d)//(2). Neglecting subsequent motion and air resistance , its velocity `v` varies with the height `h` above the ground as
View SolutionA parachutist after bailing out falls 50m without friction. When parachute opens, it decelerates at `2m//s^2`. He reaches the ground with a speed of `3m//s`. At what height, did the bail out?
View SolutionA balloon is ascending vertically with an acceelration of `0.2 ms^(-2)` .Two stones are dropped from it at an interval fo `2 s`, the distance between then when the second stone dropped is (tanke g=9.i8 ma^(-2).
View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
`v(x) = beta x^(-2 n)`
where `beta` and `n` are constant and `x` is the position of the particle. The acceleration of the particle as a function of `x` is given by.
View SolutionThe motion of a particle along a straight line is described by equation : `x = 8 + 12 t - t^3` where `x` is in metre and `t` in second. The retardation of the particle when its velocity becomes zero is.
View SolutionThe retardation fo a moving particle if the relation between time and position is ` t= A x^3 + Bx^2 ` where ` A` and ` B` are appropriate constants will be .
View SolutionThe displacement `x` of a particle varies with time `t` as `x = ae^(-alpha t) + be^(beta t)`. Where `a,b, alpha` and `beta` positive constant.
The velocity of the particle will.
View SolutionThe acceleation fo a particle (a) is related to irs velocity (v) by ` a =- v`. What is the bature of velocity-time curve ?
View SolutionAn object , moving with a speed of ` 6.25 m//s `, is decelerated at a rate given by :
`(dv)/(dt) = - 2.5 sqrt (v)` where `v` is the instantaneous speed . The time taken by the object , to come to rest , would be :
View SolutionThe deceleration exerienced by a moving motor blat, after its engine is cut-off is given by `dv//dt=-kv^(3)`, where `k` is constant. If `v_(0)` is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time `t` after the cut-off is.
View SolutionThe displacement to particle is zero at ` t=0` . It starts moving in the positive x-direction with a velocity which varies, `v= k sqrt x`, where (k) is a constant. Find the relation for variation of velocity with time.
View SolutionThe displacement of a body is given by `4s=M +2Nt^(4)`, where `M` and `N` are constants.
The velocity of the body at any instant is .
View SolutionThe retardation experienced by a movign motr bat after its engine is cut-off , at the instant (t) is given by`, ` =-k v^4` , where (k) is a constant. If ` v_0` is the magnitude of velocity at the cut-off , the magnitude fo velocity at time (t) after the cut-off is .
View SolutionThe distance traveled by an object along the axes are even by ` x= 2 t^2 , y=t^2-4 t, z=3 t -5`. The initial velocity of the particle is .
View SolutionA particle moving along x-axis has acceleration `f`, at time `t`, given by `f = f_0 (1 - (t)/(T))`, where `f_0` and `T` are constant.
The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_x)` is :
View SolutionThe x and y coordinates of the particle at any time are `x=5t-2t^(2) and y=10t` respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View SolutionA particle is moving with velocity ` vecv = k( y hat(i) + x hat(j)) `, where `k` is a constant . The genergal equation for its path is
View SolutionA particle starts from the origin of coordinates at time t = 0 and moves in the xy plane with a constant acceleration `alpha` in the y-direction. Its equation of motion is `y= betax^2`. Its velocity component in the x-direction is
View SolutionA car of mass `m` starta from rest and accelerates so that the instyantaneous power delivered to the car has a constant magnitude `P_(0)`. The instaneous velocity of this car is proportional to
View SolutionA particle of mass `m` is at rest the origin at time ` t= 0 ` . It is subjected to a force ` F(t) = F_(0) e^(-bt)` in the `x` - direction. Its speed ` v(t)` is depicted by which of the following curves ?
View SolutionThe position vector of a particle `vec(R )` as a funtion of time is given by:
`vec(R )= 4sin(2pit)hat(i)+4cos(2pit)hat(j)`
Where `R` is in meters, `t` is in seconds and `hat(i)` and `hat(j)` denote until vectors along x-and y- directions, respectively Which one of the following statements is wrong for the motion of particle ?
View SolutionIf the velocity of a particle is `v = At + Bt^2`, where `A` and `B` are constant, then the distance travelled by it between `1 s` and `2 s` is :
View SolutionA ball is thrown vertically upwards. Which of the following graph/graphs represent velocity time graph of the ball during its flight ( air resistance is neglected).
View SolutionWhich of the following graphs may not repersent variation of distance (S) with respect ot time (t) ?
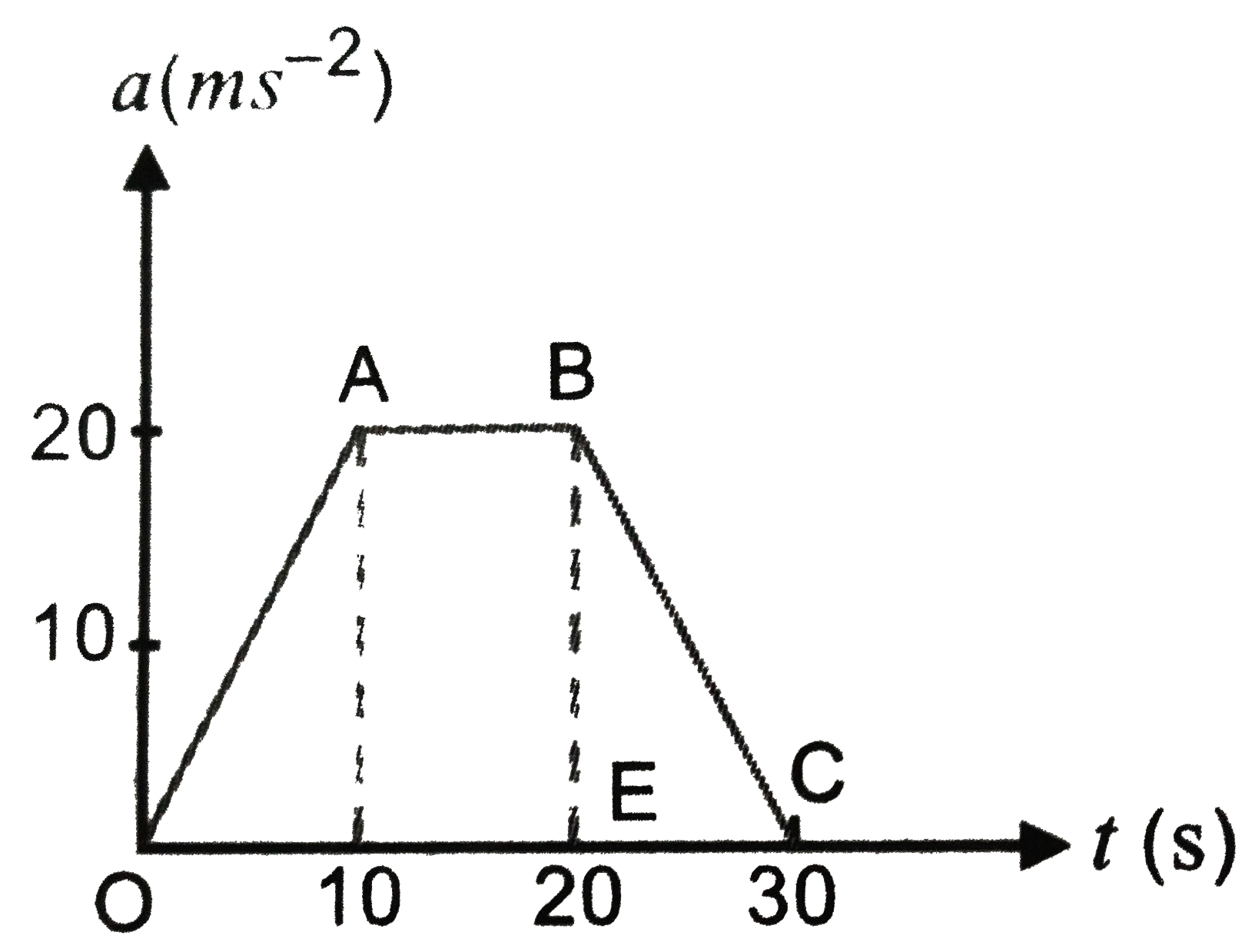
View SolutionFig. 2 (b) .16 shows the time-acceleration graph for a particle in rectillinear motion. Find the average acceleration in first twenty seconds.
 .
.
View SolutionThe velocity-time graph of a body is shown in .
The displacement of the body in `8 s` is.
 .
.
View SolutionIn the above questin, the total distance covered by the body in `8` seconds is.
View SolutionThe acceleration time graph of a particle is shown in the Fig. 2 (CF). 11. At time ` t= 10 s` is the particle is ` 8 ms^(-1)`. Its velocity ` t= 10 s` is.
 .
.
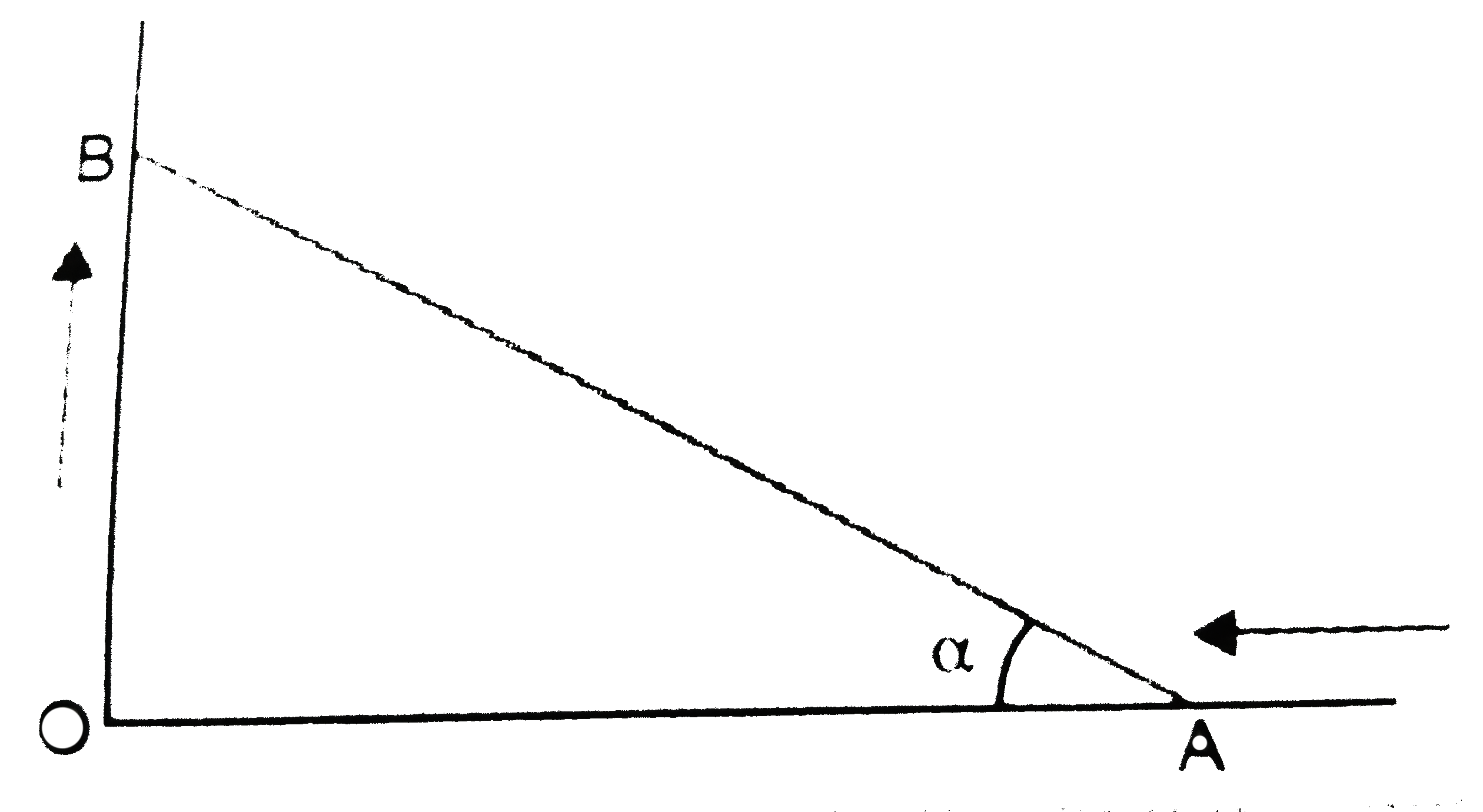
View SolutionTwo particles (A) and (B) are connected by a rigid rod ` AB`. The rod slides along perpendicular rails as shown here. The velocity of (A) to the left is ` 10 m//s`.
What is the velocity of (B) ange ` alpha = 30^@`.
 .
.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff ` 240 m ` high with initial speed of ` 10 m//s and 40 m//s` respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take ` g = 10 m//s^(2))`
( The figure are schematic and not drawn to scale )
View SolutionFor the velocity tiem graph shown in Fig. 2 (CF).14, the distance covered by the body in last two seconds of its what fraction if the total distance covered by it in all the seven seconds?
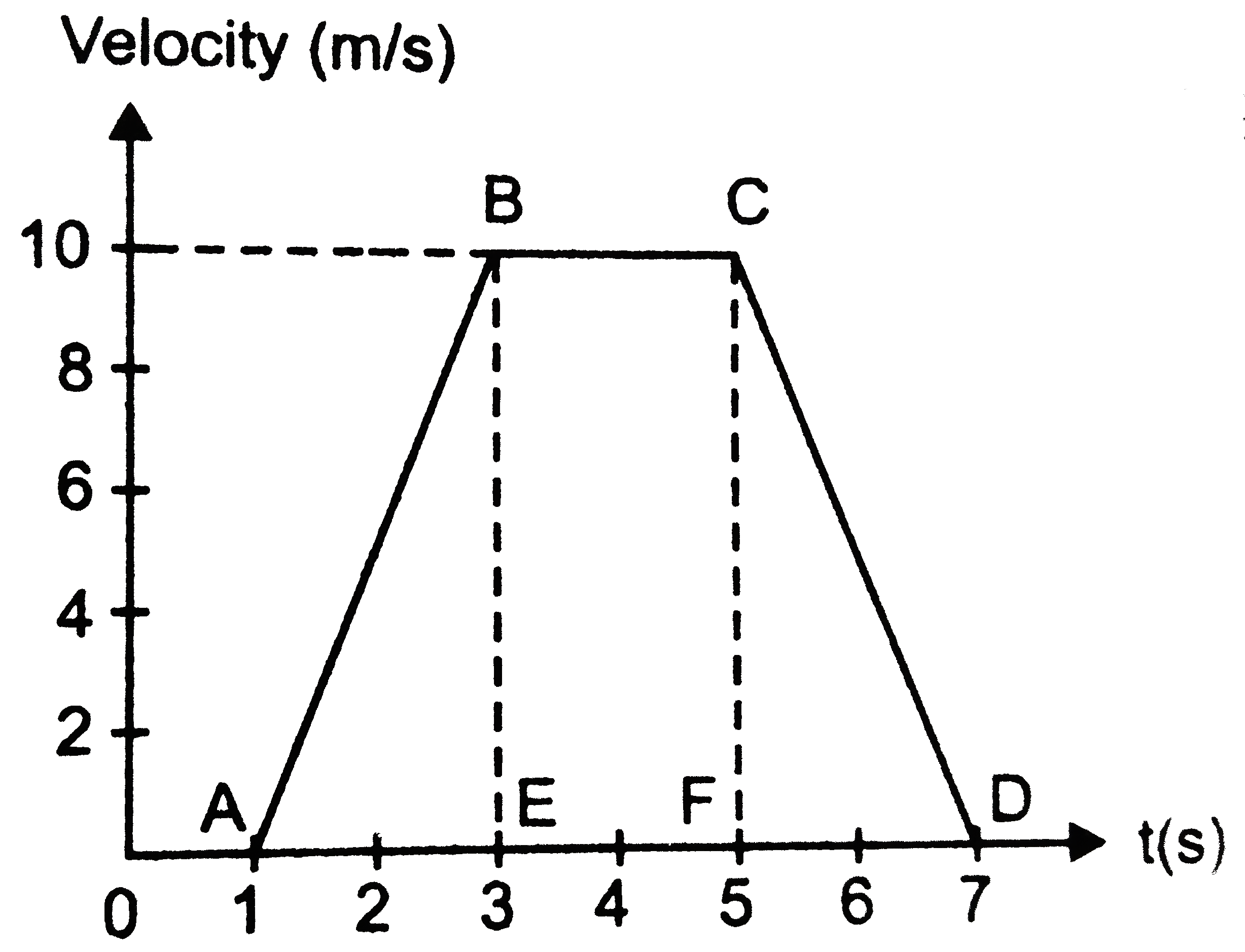 .
.
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in the Fig. 2 (CF) . 15. The distance traversed by the particle between ` t= 2 s` ` 6 s` is .
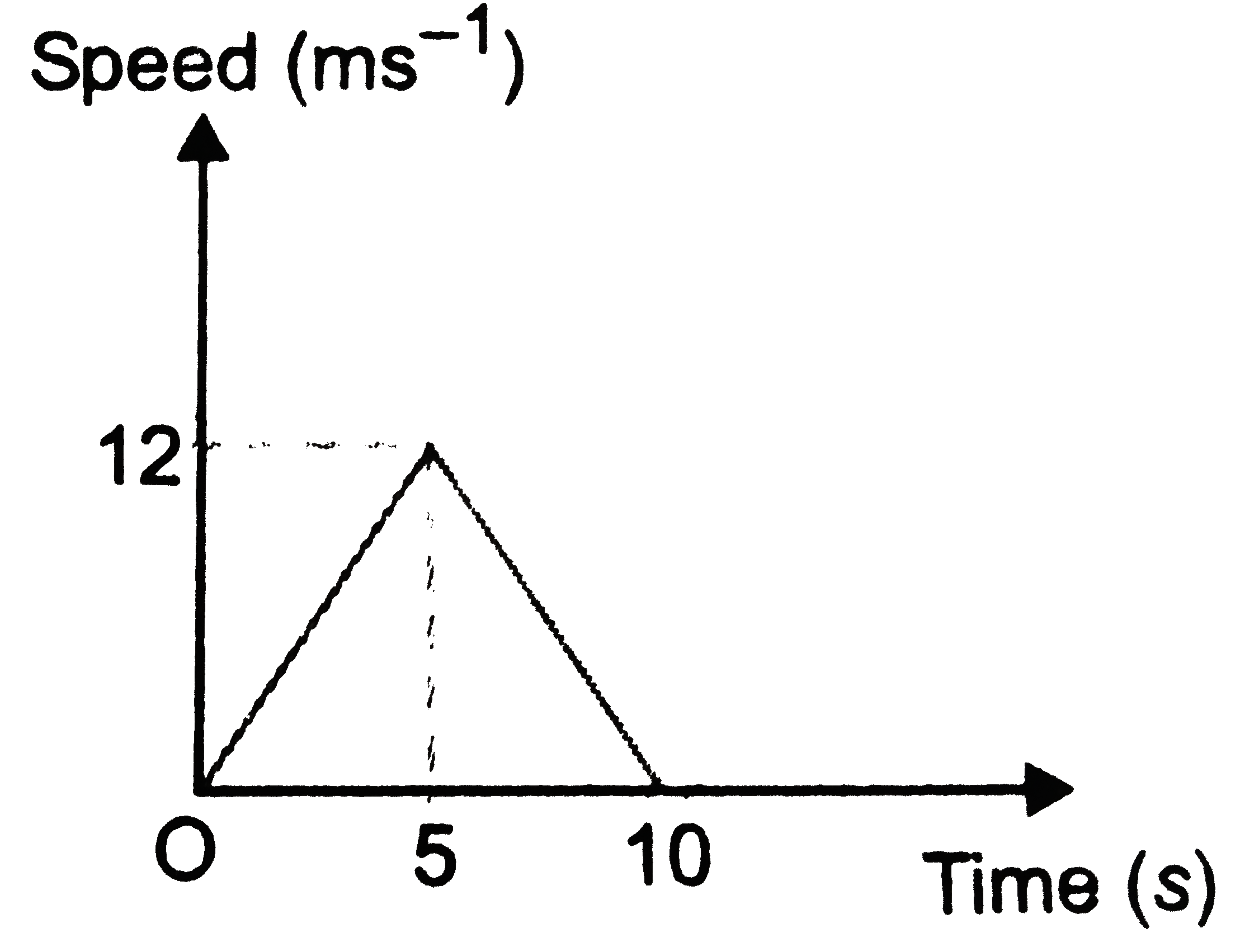 .
.
View SolutionA particle starts from rst at ` t= 0` and undergoes and acceleration (a) in ms^(-2)` with tiem (t) in seconds which is shown in Fig. 2 (DF) .16 . Which one of the following plot repesents velocity (v) (in ms_1) versis time (in seconds ) ?
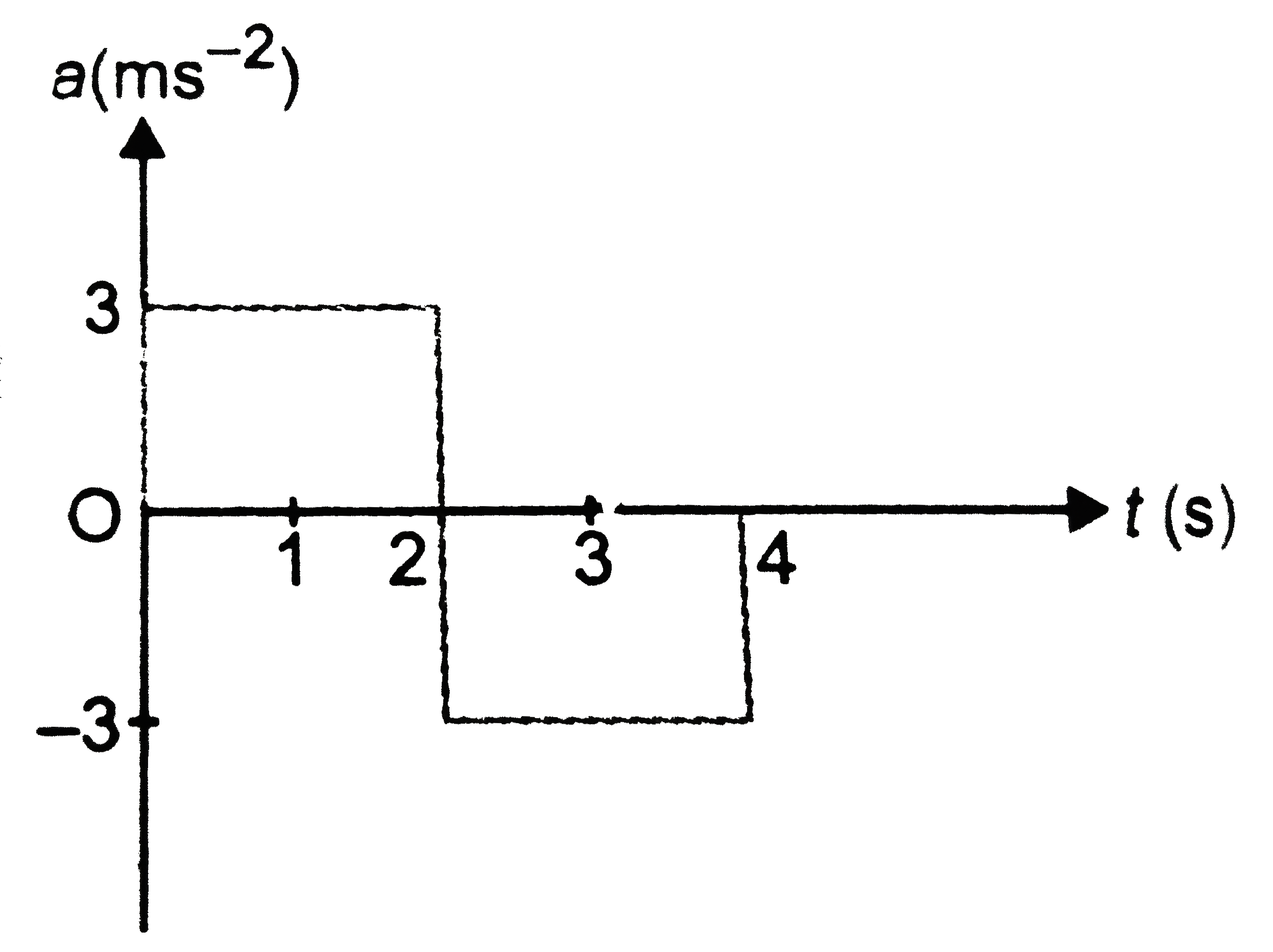
View SolutionIn the given ` v-t` graph, the distance travelled by the body in `5` second will be
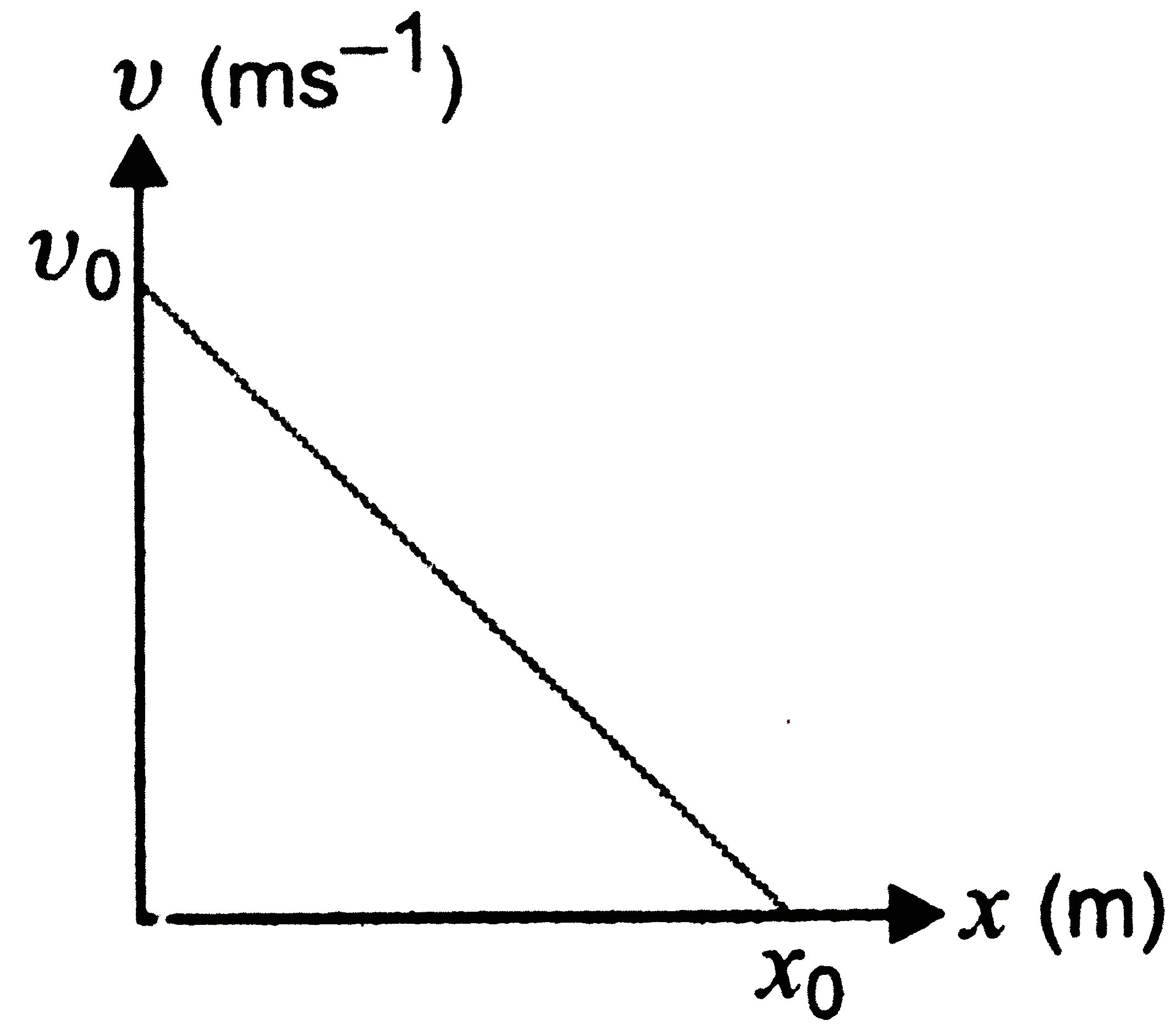 .
.
View SolutionWhat will be the (a) ve (x) graph for the graph shown in Fig. 2 (CF). 18
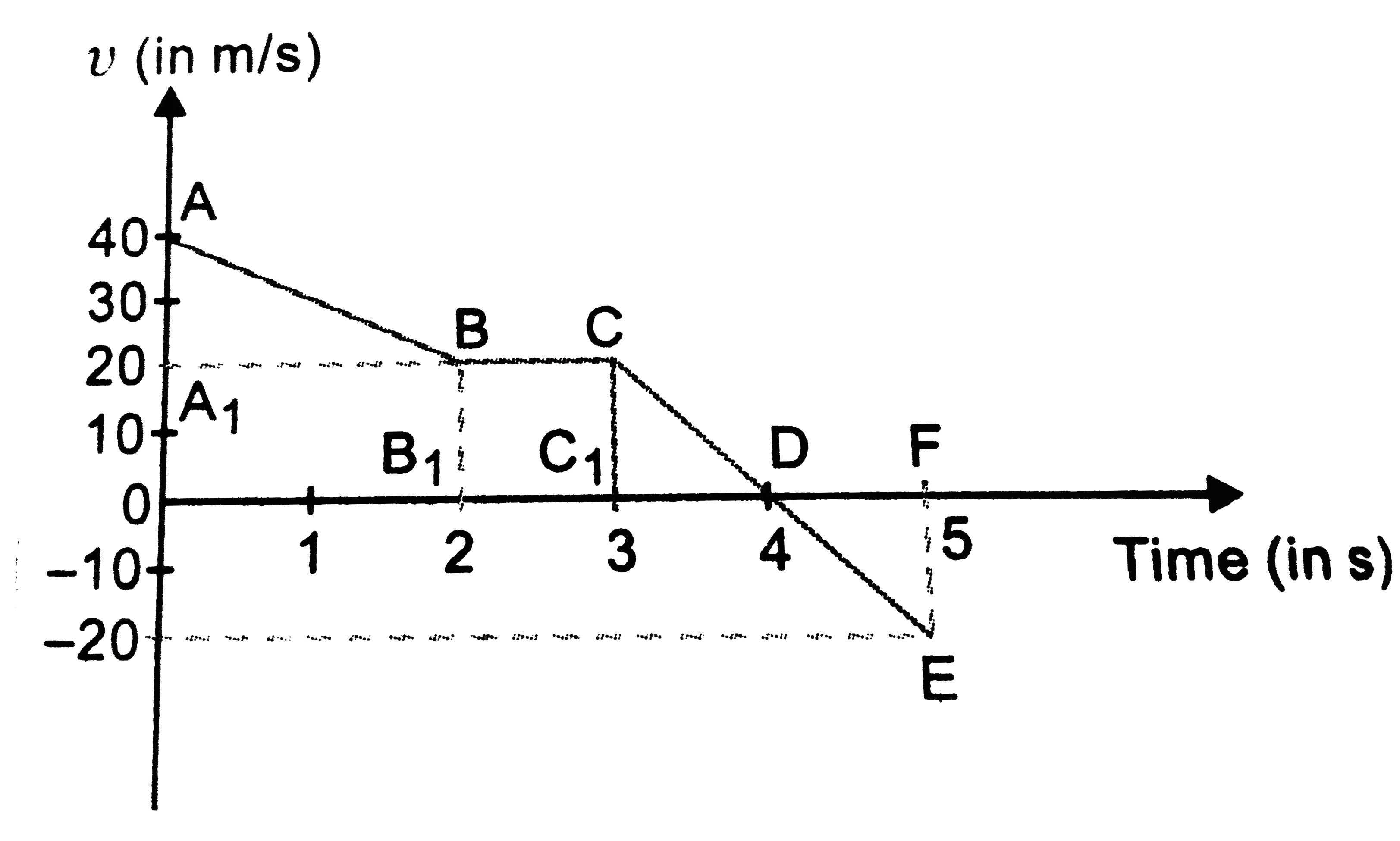 .
.
View SolutionA body is at rest at ` x =0 ` . At ` t = 0`, it starts moving in the positive `x - direction` with a constant acceleration . At the same instant another body passes through ` x= 0 ` moving in the positive ` x - direction ` with a constant speed . The position of the first body is given by `x_(1)(t)` after time 't', and that of the second body by ` x_(2)(t)` after the same time interval . which of the following graphs correctly describes `(x_(1) - x_(2))` as a function of time 't' ?
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionA particle is moving eastwards with a velocity of ` 5 m//s`. In `10 s` the velocity changes to `5 m//s` nothwards. The average acceleration in this time is
View SolutionA person moves `30 m` north, then `30 m est, then 30sqrt(2)` south-west. His diaplacement from the original position is
View SolutionA truck travelling due North at ` 50 km h^(-1)` turns Westamd travels at the same speed. What is the change in velocity ?
View SolutionA vector `vec A` of magniude (A) is turned through an angle ` theta`. Calculate the change in the magnitude of vector.
View SolutionAn aeroplane fles a straight path from town (A) to town ` B, 500 km` way . Town (B) is due East ot town (A) and a strong with blows from South to North at 1 300 km//h`. Tf the lane`s air speed is ` 900 km//h`. Which of following statements is true ?
View SolutionIn the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
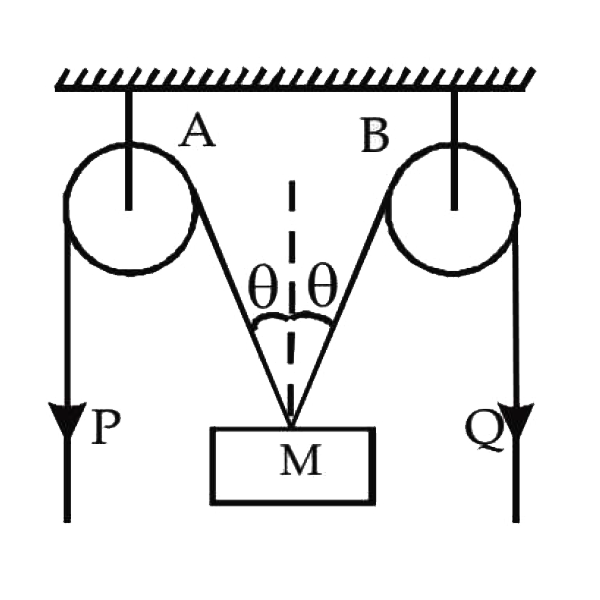
View SolutionA body is moving with velocity `30 m//s` towards east. After `10 s` its velocity becomes `40 m//s` towards north. The average acceleration of the body is.
View SolutionThe sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
View SolutionIf vector `P, Q and R` have magnitude 5,12,and 13 units and `vec(P)+vec(Q)=vec(R )`, the angle between Q and R is
View SolutionAn object of mass ` 3 kg ` is at rest. Now a force of ` vec F = 6 t^2 hat I + 4 t hat j` is applied on the object, the velocity of object at `t= 3 s` is.
View SolutionIf `vec(A)=vec(B)+vec(C )`, and the magnitudes of `vec(A)`,`vec(B)`,`vec(C )` are 5,4, and 3 units, then the angle between `vec(A)` and `vec(C )` is
View SolutionFour persons K,L,M,N are initially at the four corners of a square of side d. Each person now moves with a uniform speed v in such a way that K always moves directly towards L, L directly towards M, M directly towards N, and N directly towards K. The four persons will meet at a time............. .
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionForces of ` 5 N, 12 N` and ` 13 N` are equilibrimum. If ` sin 23^@= 5 //13 `, the angle between ` 5 N` and ` 13N` force is.
View SolutionThe resultant ot two forces acting at an angle of ` 150^@` is ` 10 N` and is perpendicular to one of the forces. The other force is .
View SolutionThe magnitude of vectors `vec(OA), vec(OB) and vec (OC)` in figure are equal. Find the direction of `vec(OA)+vec(OB)-vec(OC)`.
 .
.
View SolutionTwo unequal vectors are inclined at an angle `30^(@)`. When they are added, the resultant can be :
View SolutionThe vectors ` vec P = a hat I + a hat j + 3 hat k)` and ` vec Q = a hat I - 2 hat j - hat kl` are peroendicular to each other. The positve value of (a) is.
View Solutionthe resultant of two forces is ` 10 sqrt 13 N`, when one of the force is ` 10 sqrt 3 N` and angle between two forces is 1 30^@` then what is the value of second force ?
View SolutionThe resultant of two vectors `vec(P)` and `vec(Q)` is `vec(R )`. If the magnitude of `vec(Q)` is doubled, the new resultant vector becomes perpendicular to `vec(P)`. Then, the magnitude of `vec(R )` is equal to
View SolutionTwo vectors ` vec A` and `vec B` have equal magnitudes. If magnitude of ` vec A-vec B` is equal to (n) times the magnitude of ` vec A-vec B`, then angle between ` vec A` and ` vec B` is ?
View SolutionThe magnitude of the component of the vector
` (2 hat i+3 hat j + hat k) along (3 hat I = 4 hat k) is .
View SolutionA boat which has a speed of `5 km// hr ` in steel water crosses a river of width ` 1 km` along the shortest possible path in `15 minutes`. The velocity of the river water in ` km// hr` is
View SolutionWind is blowing west to east along two parallel tracks. Two train moving with the same speed in opposite directions on these tracks have the steam tracks. If one is double than the other, what is the speed of each train ?
View SolutionA ship travels downstream from point (A) to point (B) in two hours and upstream in three hours. Then the time taken by log wood to cover the distance from (A) to (B) is .
View Solution
3 NCERT multiple questions and complete solutions for chapter KINEMATICS of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS KINEMATICS
- 1 Problems for practice
- 1 Con ceptual Problems
- 1 Conceptual Problems
- 1 Fill in the blanks
- 1 Long answer
- 1 Multiple choice
- 1 NCERT Assertion-Reaseon Type
- 1 NCERT Comprehension
- 1 NCERT multiple
- 1 Short answer
- 1 SolvedExamples
- 1 Very short
- 2 Con ceptual Problems
- 2 Fill in the blanks
- 2 Long answer
- 2 Multiple choice
- 2 NCERT multiple
- 2 Problems for practice
- 2 Short answer
- 2 SolvedExamples
- 2 Very short
- 3 Con ceptual Problems
- 3 Fill in the blanks
- 3 Long answer
- 3 Multiple choice
- 3 NCERT multiple
- 3 Problems for practice
- 3 Short answer
- 3 SolvedExamples
- 3 Very short
- 4 Con ceptual Problems
- 4 Conceptual Problems
- 4 Fill in the blanks
- 4 Long answer
- 4 Multiple choice
- 4 NCERT Integer type
- 4 NCERT multiple Choice
- 4 Problems for practice
- 4 Short answer
- 4 SolvedExamples
- 4 Very short
- 5 Long answer (NCERT)
- 5 Short answer
- 5 Very short
- 6 Long answer (NCERT)
- 6 Short answer
- 6 Very short
- Additional Exercises
- Advanced Problems
- Higher order thinking skills
- Motion
- NCRT Exercises
- Sample Promlem
- Value based