Complete Solutions to Problems For Practice of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| PRADEEP | Problems For Practice |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
A uniform chain of length `L` and mass `M` is tying on a smoth table and one third of its length is banging vertically down table the edge of the table if g is acceleration the to gravity , the work required to pull the hanging part on the table is
View SolutionA man moves on a straight horizontal road with a block of mass 2 kg in his hand. If he covers a distance of `40m` with an acceleration of `1ms^(-2)`, find the work done by the man.
View SolutionCalculate work done in raising a stone of mass 5kg and specific gravity 3 lying at the bed of a lake through a height of 4 metre.
View SolutionA man weighing `60kg` `f` suports a body of `20kg f ` on his head. Calculate work done by him in moving a distance of `15m` up an incline of `1` in 10 . Take `g=9.8m//s^(2)`
View SolutionA body moves from a point `A` to `B` under the action of a force shown in figure. What is the amount of work done ?

View SolutionUnder the action of a force, a `2 kg` body moves such that its position x as a function of time is given by `x =(t^(3))/(3)` where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionA man weighing `55kg` supports a body of `20kg` on his head. Calculate work done by him if he moves a distance of `20m(i)` on a horizontal road, (ii) upon a smooth incline of 1 in 5. Take `g=10ms^(-2)`
View SolutionA body of mass `0.3kg` is taken up an inclined plane of length `10m` and height `5m,` and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is `0.15`.
What is the
(a) work done by the gravitational force over the round trip ?
(b) work done by the applied force on the upward journey ?
(c) work done by the frictional force over the round trip ,
(d)kinetic energy of the body at the end of the trip ?
View SolutionA force exerts an impulse `J` on a body changing its speed from `u` to `upsilon`. The force and object's motion are along the same line. Show that the work done by the force is `J(u+upsilon)//2`
View SolutionA particle moves from a point `vec (r)_(2)=(2hat(i) +3hat(j))` to another point `vec (r)_(2)=(3hat(i) +2hat(j))` during which a certain force `vec(F)=(5hat(i)+5hat(j))` acts on it. Calculate work done by the force on the particle during this displacement.
View SolutionIn a ballistic demonstration, a police officer fires a bullet of mass `50g` with a speed of `220m//s` on a wooden target. The bullet emerges with `20%` of its initial `K.E.` What is the emergent speed of the bullet ?
View SolutionMomentum of a particle is increased by `50%`. By how much percentage kinetic energy of particle will increase?
View SolutionA toy rocket of mass 0.1 kg hass a small fuel of mass 0.02 kg, which it burns out in 3s. Starting from rest on a horizontal smooth track, it gets a speed of `20ms^(-1)` after the fuel is burnt out. What is the approcimate thrust of the rocket ? What is the energy content per unit mass of the fuel ? (Ignore the small mass variation of teh rocket during fuel burning).
View SolutionWhile catching a cricket ball of mass `200g` moving with a velocity of `20ms^(-1)`, the player draws his hands backwards through `20cm`. Find the work done in catching the ball and the average force exerted by the ball on the hand.
View SolutionA body of mass `2kg` is resting on rough horizontal surface. A force `20N` is applied to it for `10s` parallel to the surface. If coefficient of kinetic friction between the surfaces in contact in `0.2.` Caluculate (i) work done by applied force in `10s`. (ii) change in `KE` of object in `10s`.
Take `g=10m//s^(2)`
View SolutionThemasses of `1g` and `4g` are moving with equal kineticc energies. Calculate the ration of the magnitudes of their linear momenta.
View SolutionLinear momentum of particle is increased by
(a) 100% (b) 1%
without changing its mass. Find percentage increase in its kinetic energy in both cases.
View SolutionAn automobile moving at a speed of `72kmh^(-1)` reaches the foot of a smooth incline, when the engine is switched off. How much distance does the automobile go up the incline before coming to rest. The angle of inclination with horizontal is `30^(@)` and `g=9.8 ms^(-2) ?`
View SolutionA bullet weighing `10g` is fired with a velocity of `800ms^(-1)`. After passing through a mud wall `1m` thick, its velocity decreases to `100ms^(-1)`. Find the average resistance offered by the mud wall.
View SolutionA body of mass `5kg` is acted upon by a variable force. The force varies with the distance covered by the body as shown in figure. What is the speed of the body when it has covered `25m`? Assume that the body starts from rest.
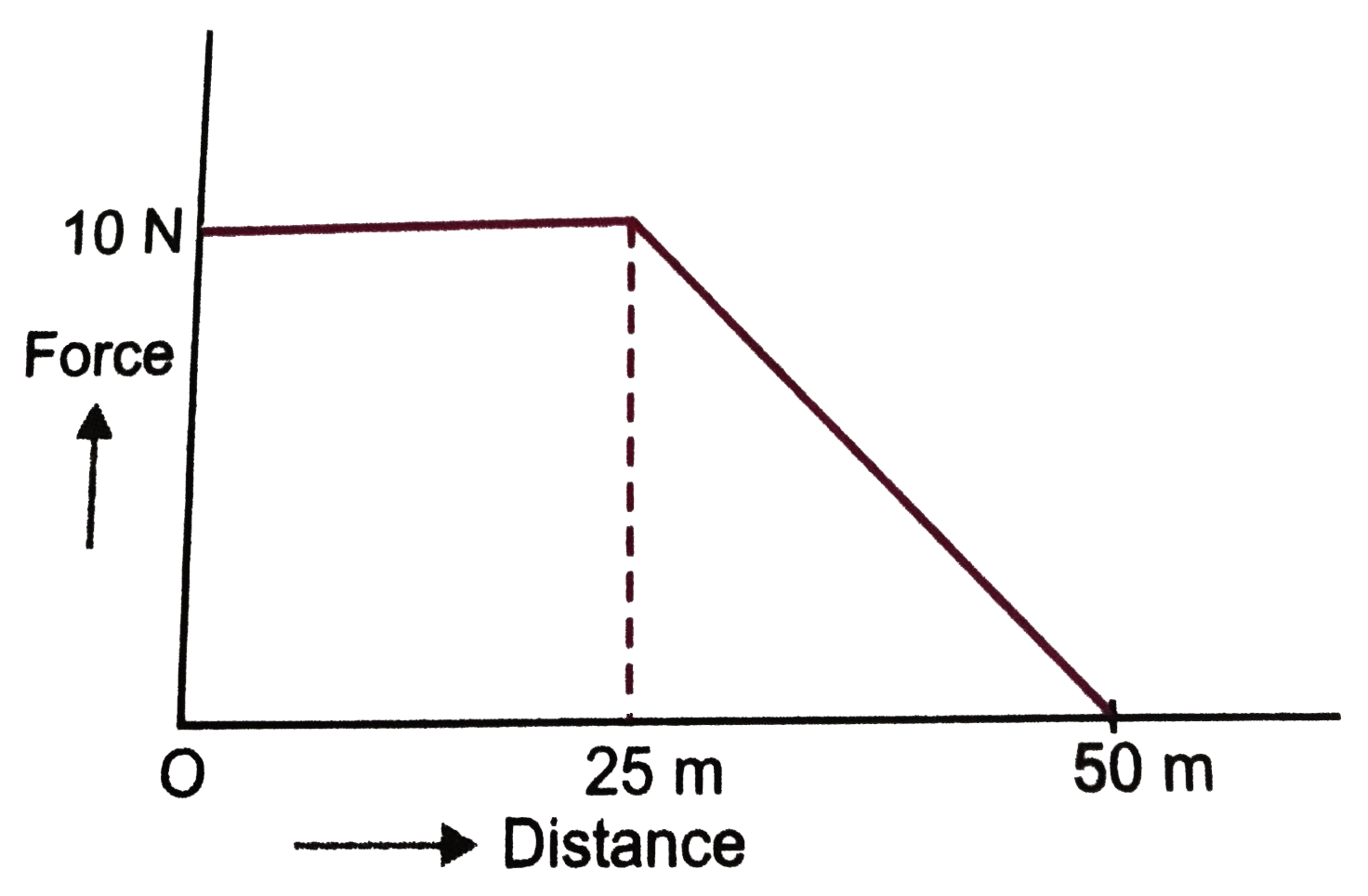
View SolutionA horizontal force of `5N` acts on a body of mass `2kg` initally at rest. It starts moving on a table having coefficient of friction `=0.2` Calculate
(i) work doen by the applied force in `5s`
(ii) work done by force of friction in `5s`
(iii) work done by net force is `5s`
(iv) change in `K.E.` of the body in `5s`.
What do you conclude from this ?
View SolutionA girl of mass `40kg` sits on a swing formed by a rope `6m` long. A person pulls the swing to a side so that the rope makes an angle of `60^(@)` with vertical . What is the gain in `P.E.` of the girl.
View SolutionA ball bounce of `80%` of its original height . What fraction of its mechanical energy is lost in each bounce ?
View SolutionA simple pendulum of length `1m` has a wooden bob of mass `1kg`. It is struck by a bullet of mass `10g` moving with a speed of `200m//s`. The bullet gets embedded into the bob. Obtain the height to which the bob rises before swinging back.
Take `g=10m//s^(2)`.
View SolutionA body dropped from a height H reaches the ground with a speed of 1.2 `sqrt(gH)`. Calculate the work done by air friction.
View SolutionA pendulum bob has a speed 3m/s while passing thorugh its lowest position. What is its speed when it makes an angle of `60^0` with the vertical? The length of the pendulum is 0.5m Take `g=10 m/s^2`.
View SolutionA `16kg` block moving on a frictionless horizontal surface with a velocity of `4m//s` compresses an ideal spring and comes to rest. If the force constant of the spring be `100N//m`, then how much is the spring commpressed ?
View SolutionThe bob of a pendulum has its rest point `1` metre below the support. The bob is pulled aside until the string makes an angle of `15^(@)` with the vertical. Upon release, with what speed does the bob swing past its rest point ?
View SolutionThe string of a pendulum is `2.0m` long. The bob is pulled sideways so that the string becomes horizontal and then the bob is released. What is the speed with which the bob arrives at the lowest point ? Assume theat `10%` of initial energy is dissipated against air resistance. Take `g=10m//s^(2)`
View SolutionA spring gun has a spring constant of `80Ncm^(-1)`. The spring is compressed `12cm` by a ball of mass `15g`. How much is the potential energy of the spring ? If the trigger is pulled, what will be the velocity of ball ?
View SolutionA ball of mass `m` is droppped from a height `h` on a platform fixed at the top of a vertical spring. The platform is depressed by a distance `x`. What is the spring constant `K`?
View SolutionThe potential energy of a certain spring when stretched through a distance 'S' is `10` joule. The amount of work (in joule) that must be done on this spring to stretch it through an additional distance 'S' will be
View SolutionA certain spring that obeys Hook's law is stretched by an external agent. The work done in stretching the spring by `10 cm is 4 J` . How much additional work is required to stretch the spring an additional `10 cm`?
View SolutionA spring of force constant 24N`//`m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
View SolutionAn object is attached to a vertical springs and lowered slowly to its equilibrium position. This stretches the spring by a distance `d`. If the same object is attached to the same vertical spring, but permitted to fall freely, through what distance does it stretch the spring ?
View SolutionAbout `4xx10^(9)kg` of matter is converted into energy in the sun each second. What is the power output of the sun ?
View SolutionShow that energy equivalent of one atomic mass unit is nearly `933MeV`.
Take `1a m u=1.66xx10^(-27)kg`
View SolutionWhat is the minimum energy released in the annhilation of an electron positron pair?
View SolutionWhen slow neutrons are incident on a target containing `._(92)U^(235)` , a possitle fission reactionis
`._(92)U^(235)+n rarr ._(56)Ba^(141)+_(36)Kr^(92)+3n+Q`
Estimate the amount of energy released using the following data :
`M[._(92)U^(235)]=235.04u,`
`M[._(56)Ba^(141)]=140.91u,`
`M[._(36)Kr^(92)]=91.926u,`
`M_(n)=1.0087u.`
Take `1u=1.661xx10^(-27)kg.`
`1MeV=1.602xx10^(-13)J`
View SolutionA nucleus of radium ` (._(88)Ra^(226))`
decays to `._(86)Rn^(222)`
by emisson of `alpha-` particle `(._(2)He^(4))` of energy `4.8MeV`. If meass of `._(86)Rn^(222)=222.0 a.m.u` mass of `._(2)He^(4)` is `4.003 ` a.m.u. and mass of `._(88)Ra^(226)` is `226.00826` a.m.u., then calculate the recoil energy of the daughter nucleus. Take ` 1 a.m.u. =931MeV`
View SolutionIf `1000kg` of water is heated from `0^(@)C` to `100^(@)C`, calculate the increase in mass of water.
View SolutionA well `20m` deep and `3m` is diameter contains water to a dept of `14m`. How long will a `5 hp` engine take to empty it ?
View SolutionAn elevator which can carry a maximum load of `1800kg` is moving with a constant speed of `2ms^(-1)`. The frictional force opposing the motino is `5000N`. Calculate the minimum power delivered by the motor to the elevator in watt and hp ?
Take `g=10m//s^(2)`
View SolutionA lift is designed to carry a load of 4000 kg through 10 floors of a building, avarage 6m per floor, in 10s. Calculate the power of the lift.
View SolutionAn engine pumps up `100 kg` water through a height of `10 m` in `5 s`. If efficiency of the engine is `60%`. What is the power of the engine? `Take g = 10 ms^(2)`.
View SolutionA pump can throw up 10 quntals of coal per hour from a coal mine `120m` deep. Calculate the power of the engine in watt assuming that efficiency is `80%`.
View SolutionFind the power of a person who can chew `30g` of ice in one minute. Latent heat of ice `=80cal//gm`, `J=4.2`joule`//`cal.
View SolutionA car of mass `2000kg` is lifted up a distance of `30m` by a crane in 1 minute . A second crane does the same job in 2 minues. Do the cranes consume the same or different amounts of fuel ? What is the power supplied by each crane ? Neglect power disspation against friction.
View SolutionWater falling from a `50m` high fall is to be used for generating electric power. If `1.8xx10^(5)kg` of water falls per hour and half the gravitational potential energy can be converted into electric energy, how many 100 watt lamps can be lit ?
View SolutionA car of mass 1000kg accelerates uniformly from rest to a velocity of `54km//h` in 5 seconds. Calculate (i) its acceleration (ii) its gain in KE (iii) average power of the engine during this period.
View SolutionA car weighing `1120kg` is going up an incline of 1 in 56 at the rate of `20m` in `2s`. Find the power of the engine if frictional force is `64N`.
View SolutionA train weighing 100 metric ton is running on a level track with a uniform speed of `72km h^(-1)` . If the frictional resistance amounts to `0.5kg` per metric ton, find the power of the engine
View SolutionAn engine of weight `6.5` metric ton is going up an inclined plane of 5 in 13 at the rate of `9km//h`. If the coefficient of friction is `(1)/(120`. Calculate the power of the engine. Take `g=9.8m//s^(2)`
View SolutionThe human heart forces `4000cm^(3)` of blood per minute through the arteries under pressure of `130mm` . The density of blood is `1.03g//c c`. What is the horse power of the heart ?
View SolutionA ball moving with a speed of `9m//s` strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of `30^(@)` with the original line of motion. Find the speeds of the two balls after collision.
View SolutionA nucleus of radium ` (._(88)Ra^(226))`
decays to `._(86)Rn^(222)`
by emisson of `alpha-` particle `(._(2)He^(4))` of energy `4.8MeV`. If meass of `._(86)Rn^(222)=222.0 a.m.u` mass of `._(2)He^(4)` is `4.003 ` a.m.u. and mass of `._(88)Ra^(226)` is `226.00826` a.m.u., then calculate the recoil energy of the daughter nucleus. Take ` 1 a.m.u. =931MeV`
View SolutionA body of mass 2 kg makes an elastic collision with another body at rest and contiues to move in the original direction with a speed equal to one thrid of its original speed. Find the mass of the second body.
View SolutionWhat percentage of `K.E.` of a moving particle is transferred to a stationary particle when it stikes the stationary particle of 4 times its mass?
View SolutionA bomb at rest explodes into two fragments of masses `3.0kg` and `1.0kg`. The total kinetic energy of the fragments is `6xx10^(4)J`. Calculate (i) , kinetic energy of the bigger fragment (ii) momentum of the smaller fragment.
View SolutionA uranium 238 nucleus, initially at rest emits an alpha particle with a speed of `1.4xx10^7m/s`. Calculate the recoil speed of the residual nucleus thorium 234. Assume that the mas of a nucleus is proportional to the mass number.
View SolutionThe first ball of mass `m` moving with the velocity `upsilon` collides head on with the second ball of mass `m` at rest. If the coefficient of restitution is `e`, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionWhat percentage of `K.E.` of a moving particle is transferred to stationary sphere particle , when it strikes the stationary particle of (a) 100 times its mass (b) equal mass ?
View SolutionWhat percentage of `K.E.` of a moving particle is transferred to a stationary particle, when moving particle strikes with a stationary particle of mass (a) 19 times in mass (b) equal in mass (c) `(1)/(19)` th of its mass ?
View SolutionA simple pendulum of length `1m` has a wooden bob of mass `1kg`. It is struck by a bullet of mass `10g` moving with a speed of `200m//s`. The bullet gets embedded into the bob. Obtain the height to which the bob rises before swinging back.
Take `g=10m//s^(2)`.
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass `2m` which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionA particle of mass `m` strikes on ground with angle of incidence `45^(@)`. If coefficient of restitution, `e=(1)/(sqrt(2))`, find the velociy after impact and angle of reflection.
View SolutionA body of mass `m` falls from a height `h` and collides with another body of same mass at rest. After collision, the two bodies combine and move through distance `(d)` till they come to rest. Find the work done against the resistive force.
View SolutionA `10kg` ball and a `20kg` ball approach each other with velocities `20m//s` and `10m//s` respectively. What are their velocities after collision, if the collision is perfectly elastic ?
View SolutionA sphere of mass `m` collides against a pendulum of mass `m` with horizontal velocity `upsilon_90)`. (i) Calculate the maximum height reached by the pendulum if the masses scatter elastically along the line of initial motion, (ii) What is the maximum height reached by the pendulum if the two masses stick together ?
View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of `0.5m//s`. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is `30cm//s`. Show that the two balls will move at right angles to eachother, after the collision.
View SolutionA ball moving with velocity `2 ms^(-1)` collides head on with another stationary ball of double the mass. If the coefficient of restitution is `0.5`, then their velocities (in `ms^(-1)`) after collision will be
View SolutionA ball of a mass m hits the floor with as speed v making an angle of incidence `theta` with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
 `
`
View SolutionFigure shows a force compression curve of a spring. A body of mass `5kg` moving with the velocity of `8m//s` hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
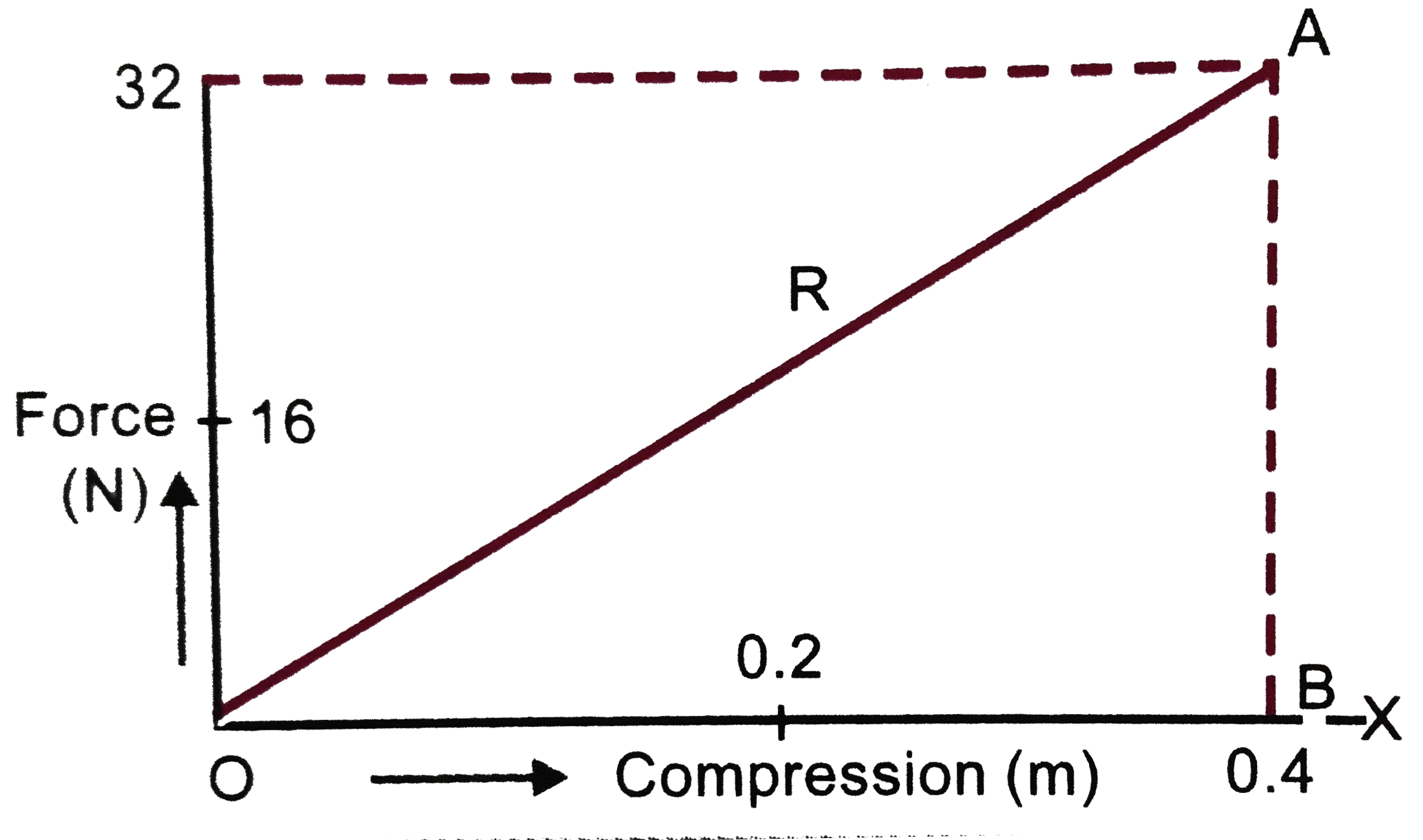
View SolutionA body falling on the ground from a height of `10m` rebounds to a height of `2.5m`. Calculate (i) the percentage loss of kinetic energy of the body during its collision with the ground. (ii) ratio of the velocities of the body just before and just after collision.
View SolutionThe iron `Fe^(27)` nucleus emits a y-axis of energy 14.4KeV. If mass of nucleus is 56.935u, calculate the recoil energy of the nucleus. Take `1u=1.66xx10^(-27)kg.`
View SolutionA particle moves in a straight line with retardatino proportional it its displacement. Calculate the loss of `K.E.` for any displacement `x`.
View Solution
Problems For Practice questions and complete solutions for chapter WORK, ENERGY AND POWER of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS WORK, ENERGY AND POWER
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- Comprehension
- Conceptual Problems
- Curiosity questions
- Fill in the blanks
- higher order thinking skills
- Integer Type Questions
- JEE (Main and Advanced)
- Long Answer Question
- Multiple choice question
- NCERT EXERCISES WITH SOLUTIONS
- NCERT( Multiple choide questions-1)
- Problems For Practice
- SAMPLE PROBLEM
- Short Answer Question
- solved examples
- value Based Question
- Very Short Anwer Question.