Complete Solutions to solved examples of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| PRADEEP | solved examples |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
A perosn is holding a bucket by applying a force of 20N. He moves a horizontal distance of 15m first and then climbs up a distance of 12m. What is the total work done by him?
View SolutionCalculate work done in raising a stone of mass 5kg and specific gravity 3 lying at the bed of a lake through a height of 4 metre.
View SolutionA uniform chain of length `2m` is kept on a table such that a length of `60 cm` hangs freely from the edge of the table. The total mass of the chain is `4 kg`. What is the work done in pulling the entire the chain the on the table?
View SolutionA cluster of clouds at a height of 1000m above the earth burst and enough rain fell to cover an area of `10^(6)m^(2)` with a depth of 2cm. How much work would have been done in raising water to the height of clouds ? Take `g=10m//s^(2)` and density of water `10^(3)kg//m^(3)`.
View SolutionA particle is acted upon by constant forces
`vec(F)_(1)=(2hat(i)-3hat(j)+4hat(k))` and `vec(F)_(2)=(-hat(i)+2hat(j)-3hat(k))` is displaced from the point `A(2,1,0)` to the point `B(-3,-4,2)`. Find the total work done by the forces.
View SolutionA particle moves along the X-axis from `x=0 to x=5m` under the influence of a force given by `F=(7-2x+3x^(2)).` Find the work done in the process.
View SolutionCalculate work done in moving the object from `x=2` to `x=3m ` from the graph shown here.
View SolutionA body moves from point A to B under the action of a force, varying in magnitude as shown in figure. Obtain the work done. Force is expressed in newton and displacement in meter.

View SolutionA force `vecF=2xhat(j)` newton acts in a region where a particle moves annticlockwise in a square loop of 2m in x`-`y plane as shown in figure . Calculate the total amount of work done. Is this force a conservative force or a non-conservative force?
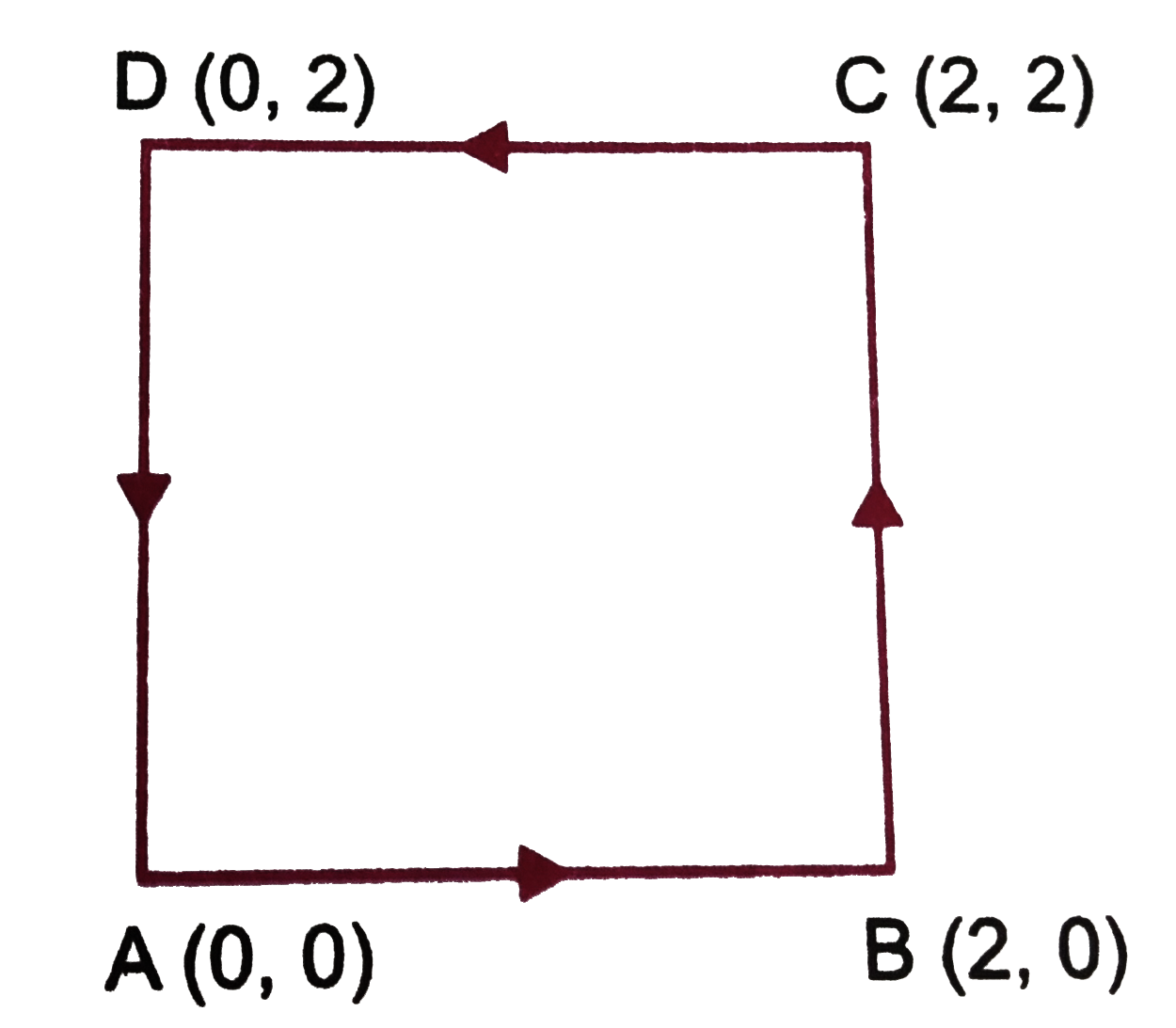
View SolutionThe displacement `x` of particle moving in one dimension, under the action of a constant force is related to the time `t` by the equation ` t = sqrt(x) +3`
where `x is in meters and t in seconds` . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first ` 6 seconds`.
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionA woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50N. The total distance through which trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50N against the distance. Calculat the work done by the two forces over 20m.
View SolutionA particle moves from position `3hat(i)+2hat(j)-6hat(k)` to `14hat(i)+13hat(j)+9hat(k)` due to a uniform force of `4hat(i)+hat(j)+3hat(k)N`. If the displacement is in meters, then find the work done by the force.
View SolutionThe variation of force acting on a body with the displacement of body is shown in figure. Calculate work done by the force in the interval
(i) `0le x lem` (ii) `2m le x le 4m`

View SolutionA shot travelling at the rate of `100m//s` is just able to pierce a plant 4 cm thick. What velocity is required to just pierce a plank 9cm thick ?
View SolutionIf KE of a body increases by `300%`, by what `%` will the linear momentum of the body increase?
View SolutionThe kinetic energy of a body decreases by `19%`. What is the percentage decrease in its momentum?
View SolutionTwo identical `5 kg` blocks are moving with same speed of `2 m//s` towards each other along a friction less horizontal surface . The two blocks collide , stick together and come to rest. Consider the two blocks as a system . The work done by the external and ijnternal force are respectively:
View SolutionA running man has half the KE that a body of half his mass has. The man speeds up by `1.0ms^(-1)` and then has the same energy as the boy. What were the original speeds of the man and the boy?
View SolutionA particle of mass `0.5kg` travels in a straight line with a velocity `v=(5x^(5//2))m//s`. How much work is done by the net force during the displacement from `x=0` to `x=2m` ?
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of `50.0ms^(-1)` (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionWhen an automobile moving with a speed of `36km//h` reaches an upward inclined road of angle `30^(@)`, its engine is switched off. If the coefficient of friction is 0.1, how much distance will the automobile move before coming to rest ? Take `g=10ms^(-2)`.
View SolutionThe mass of a pendulum bob is 0.2kg, and it is suspended by a string 1m long. It is pulled aside until the thread is at `30^(@)` to the vertical. How much work is done ? The ball is now released. Find its K.E. at the lowest point ? Take `g=10ms^(-2).`
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionTo stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of `18.0 km//h` on a smooth road and colliding with a horizontally mounted spring of spring constant `6.25xx10^(3)Nm^(-1)`. What is the maximum compression of the spring?
View SolutionConsider Example 22. Takin the coefficient of friction, `mu` to be `0.5,` calculate the maximum compression of the spring.
View SolutionExpress (a) the energy required to break one bond in DNA `(10^(-10)J)` in eV.
(b) the kinetic energy of an air molecule `(10^(-21)J)` in eV.
(c) the daily intake of a human adult `(10^(7)J)` in kilocalories.
View SolutionA body of mass 50kg has a momentum of `1000kgm//s`. Calculate its K.E.
View SolutionIf the linear momentum of a body increases by `20%`, what will be the percentage increase in KE of body ?
View SolutionA vehicles of mass 10 quintals climba up a hill 200m high and thenmoves on a level road with a velocity of `36km//h` .Calculate its total mechanical energy while running on the top of the hill.
View SolutionA ball falls undal gravity from a height of 10m with an initial downward velocity u. It collides with ground, loses halft its energy and then rises back to the same height. Find the initial velocity u.
View SolutionA bullet of mass 10g travels horizontally with speed `100m//s` and is absorbed by a wooden block of mass 900 g suspended by a string. Find the vertical height through which the block rises. Given `g=10m//s^(2)`
View SolutionTwo masses as shown in figure. Are released from their positions. Calculate the velocity with which the mass of 5kg touches the surface if its initial heigth from the surface is 4m. Also, show that the gain in KE of the system is equal to loss in its P.E. Take `g=10ms^(-2)`.

View SolutionIn a ballistics demonstration, a police officer fires a bullet mass `50.0g` with speed `200ms^(-1)` on soft plywood of thickness 2.00cm. The bullet emerges only with `10%` of its initial kinetic energy. What is the emergent speed of the bullet ?
View SolutionA force is acting on a body moving alonog x-axis in the direction of motion of the body. If this force produces a potential energy `u=Ax^(4),` where `A=1.2Jm^(-4),` then the what is the force acting on the body when the body is at `x=-0.8m`?
View SolutionA 3.0kg block has a speed of `2m//s` A and `6m//s` at B. If the distance from A and B along the curve is 12m, how large a frictional force acts on it ? Assuming the same friction, how far from B will it stop ?
View SolutionTwo springs have force constants `K_(1)` and `K_(2)` , where `K_(1)gtK_(2)`. On which spring, more work is downe if
(i) they are stretched by the same force?
(ii) they are stretched by the same amount?
View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA spring of force constant 24N`//`m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
View SolutionTwo blocks`A` and`B` are connected to each other by a string and a spring , the spring pases and a frictionlesss pulley as down over in the figure . Block `B` sides over the horizental top surface of a strionry block `C` both with the verical side of `C` , both with the same conform speed
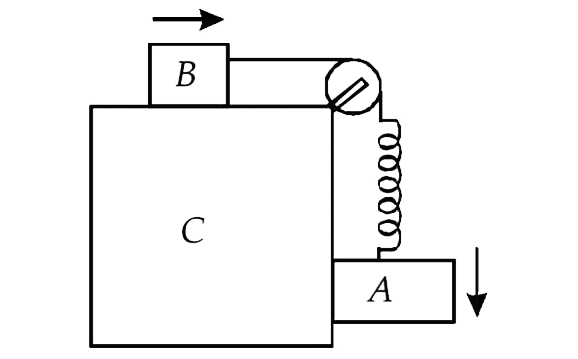
The coefficient of friction between the surface the of block is `0.2` force constant of the spring is `1960` newtons , if mass of block `A` is `2` kg , celculate the mass of block `F` and `B` and the energy stored is the spring
View SolutionIf a body of mass m suspended by a spring comed to rest after a downward displecemtn `y_(0)`, claculate (a) force constant of the spring, (b) loss in gravitational potential energy, (c) gain in elastic potential energy of spring.
View SolutionA block of mass `5.7kg` slides on a horizontal frictionless table with a constant speed of `1.2ms^(-1)`. It is brougth momentarily to rest by compressing a spring in its path. By what maximum distance is the spring compressed ? The spring constant `k=1500Nm^(-1).`
View SolutionEstimate the amount of energy released in the nuclear fusion reaction:
`_(1)H^(2)+._(1)H^(2)rarr._(2)He^(2)+._(0)n^(1)` Given that
`M(._(1)H^(2))=2.0141u, M(._(2)He^(3))=3.0160u`
`m_(n)=1.0087u` ,
where `1u=1.661xx10^(-27)kg` .
Express your answer in units of MeV.
View SolutionA particle of rest mass `m_(0)` moves with a spess `c//2` . Calculate its
(i) mass (ii) momentum (iii) total energy (iv)K.E.
View SolutionHow much mass is converted into tenergy per day in a nuclear power plant operated at `10^(7)` kW?
View Solution200 kg of water is heated from `20^(@)C` to `100^(@)C`. If specifice heat of water is `4.2xx10^(3)Jkg^(-1)0C^(-1)`, calculate the increase in the mass of water.
View SolutionA car of mass 1000kg accelerates uniformly from rest to a velocity of `54km//h` in 5 seconds. Calculate (i) its acceleration (ii) its gain in KE (iii) average power of the engine during this period.
View SolutionAn electric motor is used to lift an elevator and its load (total mass 1500kg) to a height of 20m. The time taken for the job is 20s. What work is done ? What is the rate at which work is done. If efficiency of the motor is `75%`, at which rate is the energy supplied to the motor?
View SolutionA machine gun fires 60 bullets per minute with a velocity of `700ms^(-1)`. If each bullet has a mass of 50g, find the power of the gun.
View SolutionA man cycles up a hill whose slope is 1 in 20 with a velocity of `6.4 km h^(-1)` along the hill. The weight of the man and the cycle is 98kg. What work per minute is the man doing ? What is his horse power ?
View SolutionThe human heart discharges 75ml of blood at each beat against a pressure of 0.1m of Hg. Calculate the power of the heart assuming that the pulse frequency is 80 beats per minute. Given, density of mercury `=13.6xx10^(3) kg//m^(3)`
View SolutionAn elevator can carry a maximum load of `1800 kg` (elevator + passengers) is moving up with a constant speed of `2 ms^(-1)`. The friction force opposite the motion is `4000 N`.What is minimum power delivered by the motor to the elevator?
View SolutionA standard car developes 40 H.P. Find the maximum speed the car can attain agains a resistance of 20kg wt. due to air and friction. Gvien efficiency of the engin is `25%.1H.P.=746W ` and `g=10ms^(-2)`.
View SolutionThe turbine pits at Niagra Falls are 50m deep. The average horse power develop is 5000. If the efficiency of the generator `85%` , how much water passes through the turbine per minute ? Take `g=10m//s^(2)`.
View SolutionA railway carriage of mass 9000kg moving with a speed of `36kmh^(-1)` collides with a stationary carriage of the same mass. After the collision, the two get coupled and move together. What is this common speed ? What type of collision is this?
View SolutionA ball is dropped from a heigth H. It rebounds from the ground a number of times. If coefficient is e, to what height does it go after nth rebounding ?
View SolutionA plastice ball is dropped from a height of 1m and rebounds several times from the floor. IF1.3 s elaspes from from the moment it is dropped to the second impact with the floor, what is the coefficient of restitution?
View SolutionA ball of 0.1 kg makes an elastic head on collision with a ball of unknown mass that is initially at rest. If the 0.1kg ball rebounds at one third of its original speed, what is the mass of the other ball?
View SolutionA body of mass M at rest is struck by a moving body of mass. Prove that the fraction of the initial kinetic energy of mass transferred to the struck body is `(4Mm)/((m+M)^(2))`
View SolutionIn a nuclear reactor, a neutron of high speed `(~~10^(7)ms^(-1))` must be slowed down to `10^(3)ms^(-1)` so that it can have a high probality of interacting with isotipe `_92U^(235)` and causing it to fission. Show that a neutron can lose most of its K.E. in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a fewe times the neutron mass. The material making up the light nuclei usually heavy water `(D_(2)O)` or graphite is called modertaor.
View SolutionConsider the collision depicted in Figure, to be between two billiard balls with equal masses `m_(1)=m_(2)`. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle `theta_(2)=phi=37^(@)`. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain `theta_(1)=theta` .
View SolutionA and B are two particles having the same mass m. A is moving along X-axis with a speed of `10ms^(-1)` and B is at rest. After undergoing a perfectly elastic collision with B, particle A gets scattered through an angle of `30^(@)`. What is th edirection of motion of B, and the speeds of A and B, after the collision?
View SolutionTwo particles A and B of masses m and 2m are moving along the X-axis and Y-axis respectively with the same speed v. They collide at the origin and coalesce into one body, after the collision. What is the velocity of this coalesced mass? What is the loss of energy during this collision?
View SolutionTwo particles of masses 0.5 kg and 0.25kg moving with velocity 4.0 m`//`s and -3.0m`//` collide head on in a perfectly inelastic collision. Find the velocity of the composite particle after collision and KE lost in the collision.
View SolutionA toy rocket of mass 0.1 kg hass a small fuel of mass 0.02 kg, which it burns out in 3s. Starting from rest on a horizontal smooth track, it gets a speed of `20ms^(-1)` after the fuel is burnt out. What is the approcimate thrust of the rocket ? What is the energy content per unit mass of the fuel ? (Ignore the small mass variation of teh rocket during fuel burning).
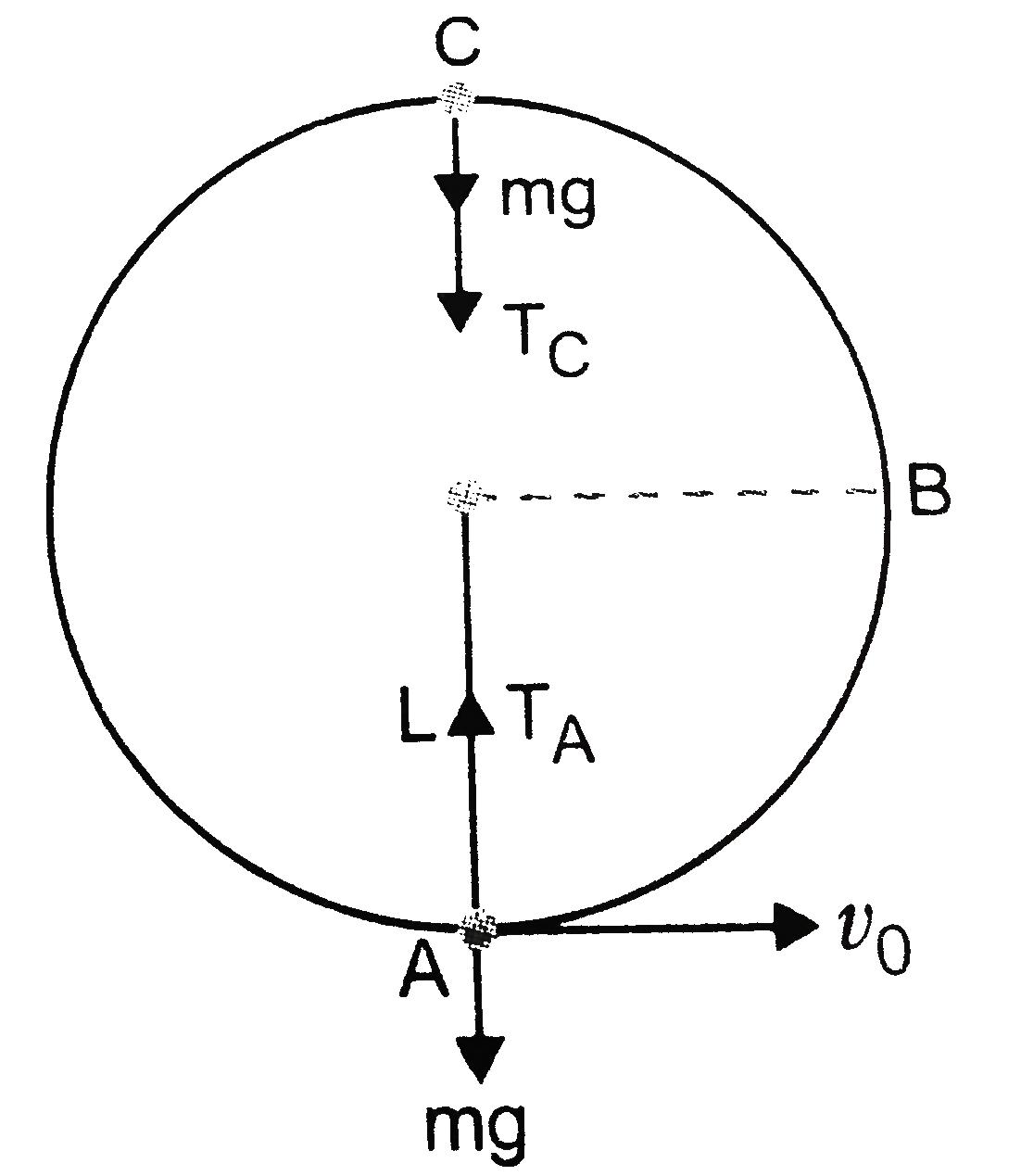
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
View SolutionA ball moves along a curved path of radius 5m as shown in figure. It starts from point A and reaches the point B. Calculate the normal force that acts on the ball at B, assuming that there is no friction between the ball and the surface of contact.
View SolutionA bullet of mass `m` hits a target of mass M hanging by a string and gets embeded in it. If the block rises to a height h as a result of this collision, the velocity of the bullet before collision is
View SolutionA uniform chain of mass m & length L is kept on a smooth horizontal table such that `(L)/(n) `portion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionAparticle of mass 1 g executes an oscillatory motion on the concave surface of a spherical dish of radius 2m placed on a horizontal plane, Figure . If the motion of the particle begins from a point on the dis at a height of 1 cm. from the horizontal plane and coefficient of friction is 0.01 , fing the total distance covered by the particle before coming to rest.

View SolutionA particle of mass 0.1kg has an iniital speed of `4ms^(-1)` at a point A on a roudh horizontal road. The coefficient of friction between the object and road is 0.15. The particle moves to a point B at a distance of 2m from A. What is the speed of particle at B ?
Take `g=10ms^(-2)`
View SolutionA 100 metric ton engine is moving up a slope of gradient `5^(@)` at a speed of 100 metre`//` hour. The coefficient of friction between the engine and the rails is 0.1. If engine has an efficiency of `4%` for converting heat into work, find the amount of coal the engine has to burn in one hour. Burning of 1 kg coal yields 50000J.
View SolutionA ball moving with a speed of `9m//s` strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of `30^(@)` with the original line of motion. Find the speeds of the two balls after collision.
View Solution
solved examples questions and complete solutions for chapter WORK, ENERGY AND POWER of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS WORK, ENERGY AND POWER
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- Comprehension
- Conceptual Problems
- Curiosity questions
- Fill in the blanks
- higher order thinking skills
- Integer Type Questions
- JEE (Main and Advanced)
- Long Answer Question
- Multiple choice question
- NCERT EXERCISES WITH SOLUTIONS
- NCERT( Multiple choide questions-1)
- Problems For Practice
- SAMPLE PROBLEM
- Short Answer Question
- solved examples
- value Based Question
- Very Short Anwer Question.