Complete Solutions to PROBLEMS FOR PRACTICE of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| PRADEEP | PROBLEMS FOR PRACTICE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A simple harmonic motion is represented by
`x=10sin(20t+0.5).`
Write down its amplitude, angular frequency, frequency, time period and initial phase if displacement is measured in metres and time seconds.
View SolutionA body oscillates with SHM according to the equation
`x(t)=5cos(2pit+pi//4)`
where t is in second and x in metres. Calculate (a) displacement at t=0 (b) time period (c) initial velocity
View SolutionA particle executes SHM of time period 10 seconds. The displacment of particle at any instant is given by `: x=10 sin omegat ` (in cm). Find (i) the velocity of the body 2 s after it passes through mean position (ii) the acceleration 2 s after it passes the mean position.
View SolutionA body is vibrating with SHM of amplitude 15 cm and frequency 4 Hz. Compute the maximum values of the acceleration and velocity.
View SolutionA particle is moving in SHM in a straight line. When the distance of the particle from equilibrium position has values `x_(1)` and `x_(2)` , the corresponding values of velocities are `u_(1)` and `u_(2)`. Show that time period of vibration is `T=2pi[(x_(2)^(2)-x_(1)^(2))/(u_(1)^(2)-u_(2)^(2))]^(1//2)`
View SolutionA particle executes SHM of period `1.2 s` and amplitude `8cm`. Find the time it takes to travel `3cm` from the positive extremity of its oscillation. `[cos^(-1)(5//8) = 0.9rad]`
View SolutionA particle executes SHM of amplitude 20cm and time period 2s. What is the minimum time required for the particle to move between two points 10cm on either side of the mean position?
View SolutionA particle moving with SHM in a straight line has a speed of `6m//s` with when 4m from the centre of oscillation and a speed of `8m//s` when 3m from the centre of oscillation . Find the amplitude of oscillation and the shortest time taken by the particle in moving from the extremen position to a point mid way between the extreme position and the centre.
View SolutionA body executes SHM under the influence of one force with a time period of 0.8second. It has a time period of 0.6 second udner the action of another force. Calculate the time period when both the force act in the same direction simultaneously.
View SolutionFrom the figure, obtain the equation of simple harmonic motion of the y-projection of the radius vector of the revolving particle P in each case.
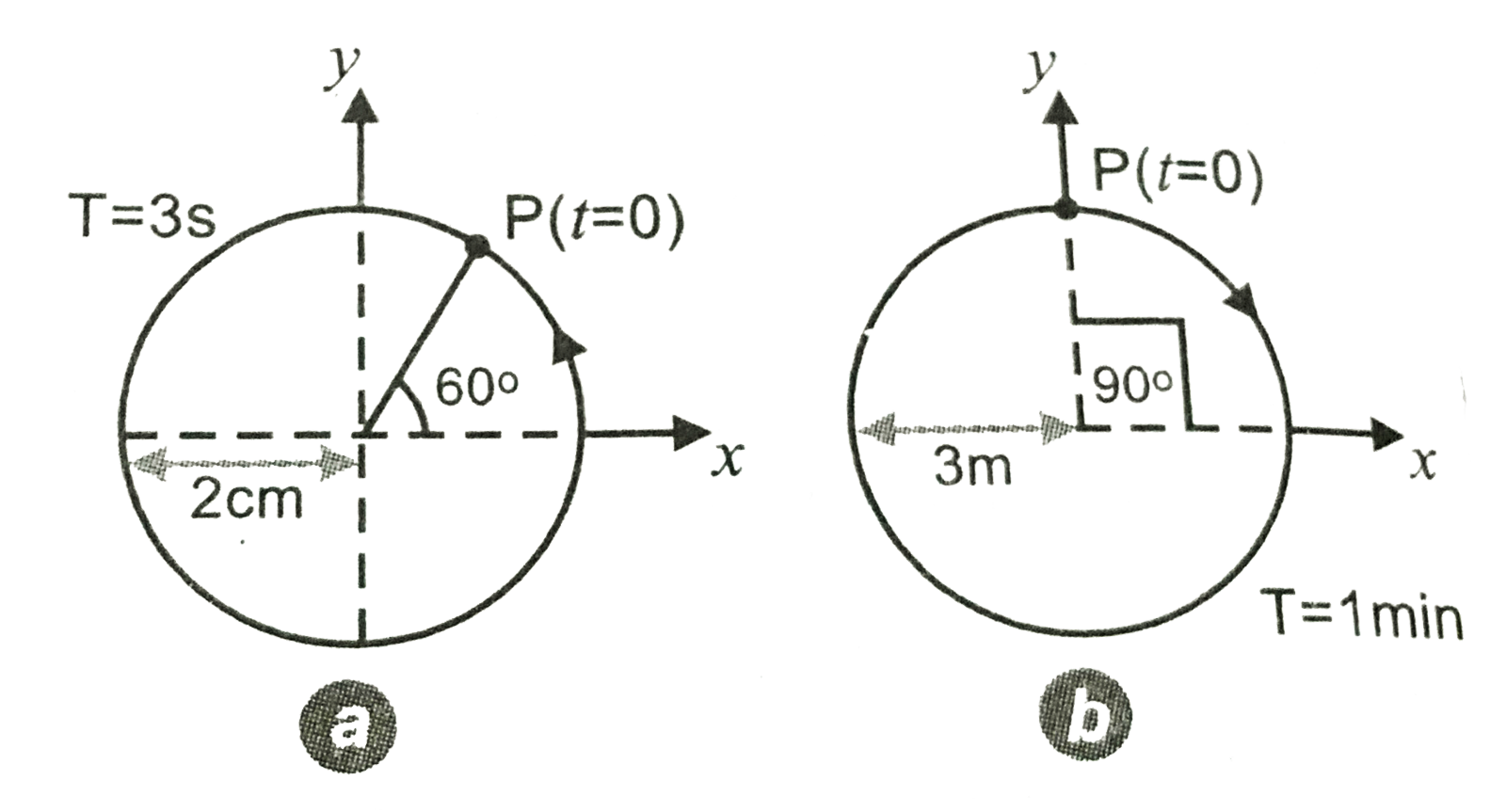
View SolutionTwo particles execute simple harmonic motion of same amplitude and frequency along the same straight line. They pass on another, when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
View SolutionThe displecement-time equation of a particle executing `SHM` is `x = A sin (omega t + phi)` At time `t = 0` position of the position is `x = A//2` and it is moving along negative `x- direction` .Then the angle `phi` can be
View SolutionMaximum velocity of a particle in SHM is 10 cm`//`s . What is the average velocity during motion from one extreme position to other extreme position ?
View SolutionA person normally weighing `60 kg` stands on a platform which oscillates up and down harmonically at a frequency `2.0 sec^(-1)` and an amplitude `5.0 cm` . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, `Take g = 10 m//sec^(2)`.
View SolutionA block lying on a horizontal table executes SHM of period 1 second, horizontally. What is the maximum amplitude for which the block does not slide if coeff. Of friction between block and surface is `0.4, pi^(2)=10. `
View SolutionIf the displacement of a moving point at any time is givenby an equation of the form `y (t) = a cos omega t + b sin omega t`, shown that the motion is simple harmonic . If `a = 3 m, b = 4m and omega = 2`: determine the period , amplitude, maximum velocity and maximum acceleration.
View SolutionTwo linear SHM of equal amplitudes `A` and frequencies `omega` and `2omega` are impressed on a particle along `x` and `y - axes` respectively. If the initial phase difference between them is `pi//2`. Find the resultant path followed by the particle.
View SolutionTwo simple harmonic motions are represented by the following equations
`y_1=10sin(3pit+pi/4)`
`y_2=5(sin 3pit+sqrt3cos3pit)`
Find out the ratio of their amplitudes. What are the time periods of two motions?
View SolutionA block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and piston separate? What is the maximum velocity of the piston at this amplitude?
View SolutionA block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency `3Hz` in a horizontal plane. The coefficient of static friciton between block and the table surface is `0.72.` find the maximum amplitude of the table at which the block does not slip on the surface.
View SolutionThe displacement of a particle executing SHM is given by `y=cos^(2)(t//2)sin(1000t).` Finid the independent constituent SHM's.
View SolutionIn a HC1 molecule, we may treat C1 to be of infinite mass and H along oscillating. If the oscillations of HC1 molecule shows frequency `8xx10^(13)s^(-1)`, deduce the force constant. Avogadro's number `=6xx10^(26)` per kg mol.
View SolutionA particle executes SHM of period 8 seconds. After what time of its passing through the mean position will the energy be half kinetic and half potential ?
View SolutionA particle of mass 10g is describing SHM along a straight line with a period of 4s and amplitude 12 cm. What is the kinetic energy when it is (i) 3cm (ii) 6 cm from its equilibrium position. How do you account for the difference between the two values ? `[use pi^(2)=10]`
View SolutionA body weighing 20 g has a velcoity `8cms^(-1)` after one second of its starting from mean position. If the time period is 8 seconds, find the kinetic energy, potential energy and total energy.
View SolutionWhen the displacement is one half of the amplitude, what fraction is potential in SHM ? At what displacement is the energy half kinetic and half potential?
View SolutionA linear harmonic oscillator of force ocnstant `2xx10^(6)N//m` and amplitude 0.01 m has a total mechanical energy of 160J. What is the maximum K.E. and minimum P.E.?
View SolutionA particle executes SHM with an amplitude 4 cm. Locate the position of point where is speed is half its maximum speed. At what displacement is potential energy equal to kinetic energy?
View SolutionA particle executes simple harmonic motion of amplitude A (i) At what distance from the extreme positino is its kinetic energy equal to half its potential energy ? (ii) At what position from the extreme position is its speed half the maximum speed.
View SolutionA spring of force constant `1200Nm^(-1)` is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released , what is
(a) The speed of the mass when the spring is compressed by 1.0cm?
(b) Potential energy of the mass when it momentarily comes to rest ?
(c) Total energy of the oscillating mass.

View SolutionA 5 kg collar is attached to a spring of spring constant 500`Nm^(-1)` . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA 0.2kg of mass hangs at the end of a spring. When 0.002kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed what will be the period of vibration of the system?
View SolutionThe frequency of oscillations of a mass m suspended by spring of `v_(1)`. If the length of the spring is cut to one-third, the same mass oscillates with frequency `v_(2)`. Determing the value of `v_(2)//v_(1)`
View SolutionA spring is of spring constant `k=15 N//cm`. It is cut into 3 equal parts, which are joined in parallel. What is the spring constant of the combination ?
View SolutionA body of mass 10 kg is suspended by a massless coil spring of natural length 40 cm and force constant `2.0xx10^(3)Nm^(-1)`. What is stretched length of the spring.? If the body is pulled down further stretching the spring to a length 48cm and then released, what is the frequency of oscillations of the suspended mass ? `g=10ms^(2)`
View SolutionInfinite springs with force constants k,2k, 4k and 8k … respectively are connected in series. What will be the effective force constant of springs, when `k=10N//m`
View SolutionTwo springs of equal lengths and equal cross-sectional area are made of materials whose Young's moduli are in the ration of `2:3` . They are suspended and loaded with the same mass. When stretched and released they oscillate. Find the ratio of the time period of oscillation.
View SolutionA spring of constant `k=0.5 N//m` and an attached mass m oscillates on a smooth horizontal table. When the mass is at position `x_(1)=0.1m, ` its velocity is `v_(1)=-1ms^(-1)` , and at `x_(2)=0.2m`, it has velocity `v_(2) =0.5ms^(-1)`. Find m and the amplitude A of the motion.
View SolutionA force of 1N is required to stretch a spring by 1.5cm. If the spring is cut into three equal parts, find the force required to stretch one part by 3 cm.
View SolutionTwo particles A and B of equal masses are suspended from two massless springs of spring constants `k_(1)=4N//m` and `k_(2)=8 N//m` respectively. If maximum velocities during oscillation are equal, fing the ration of amplitudes of A and B.
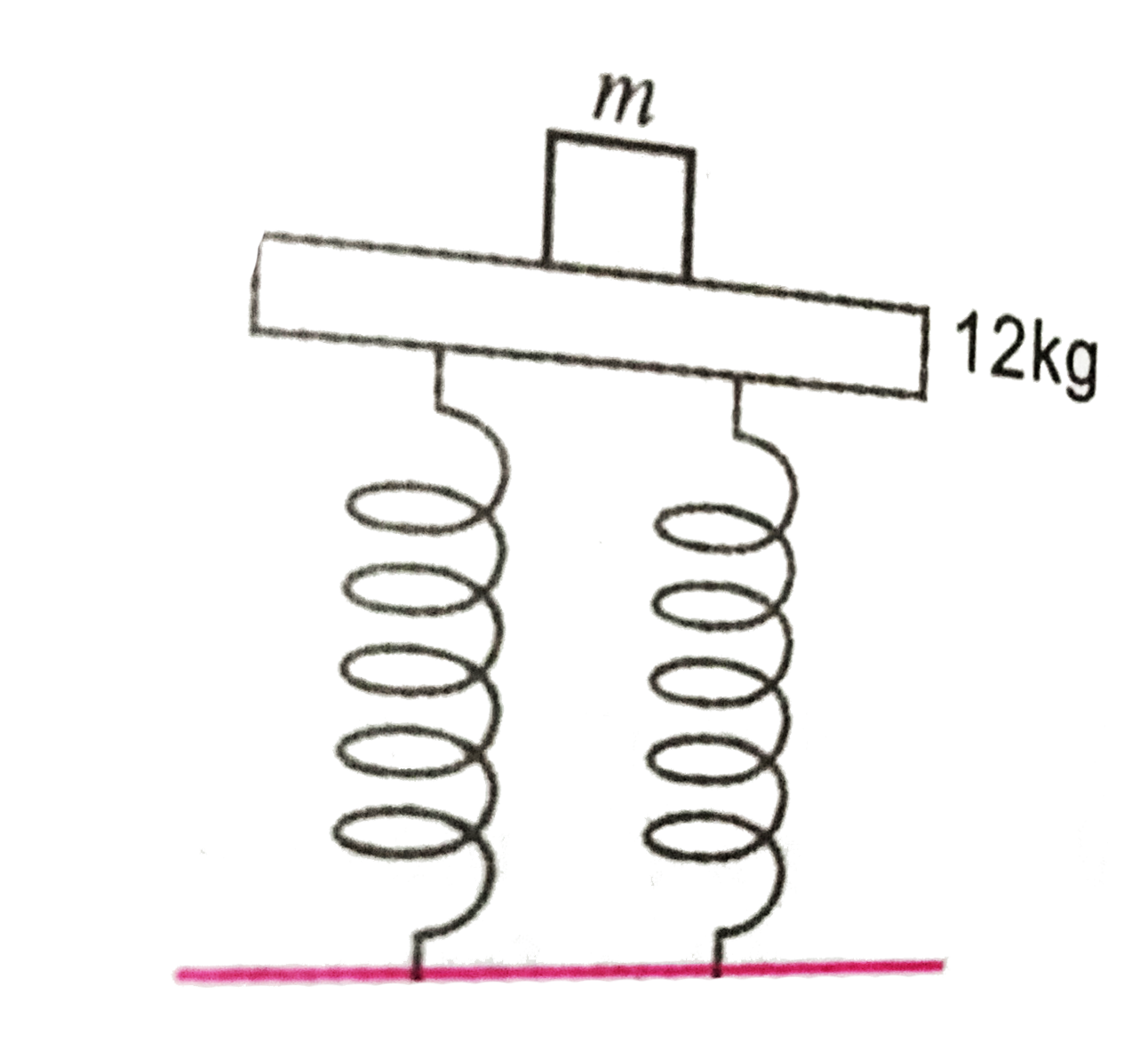
View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
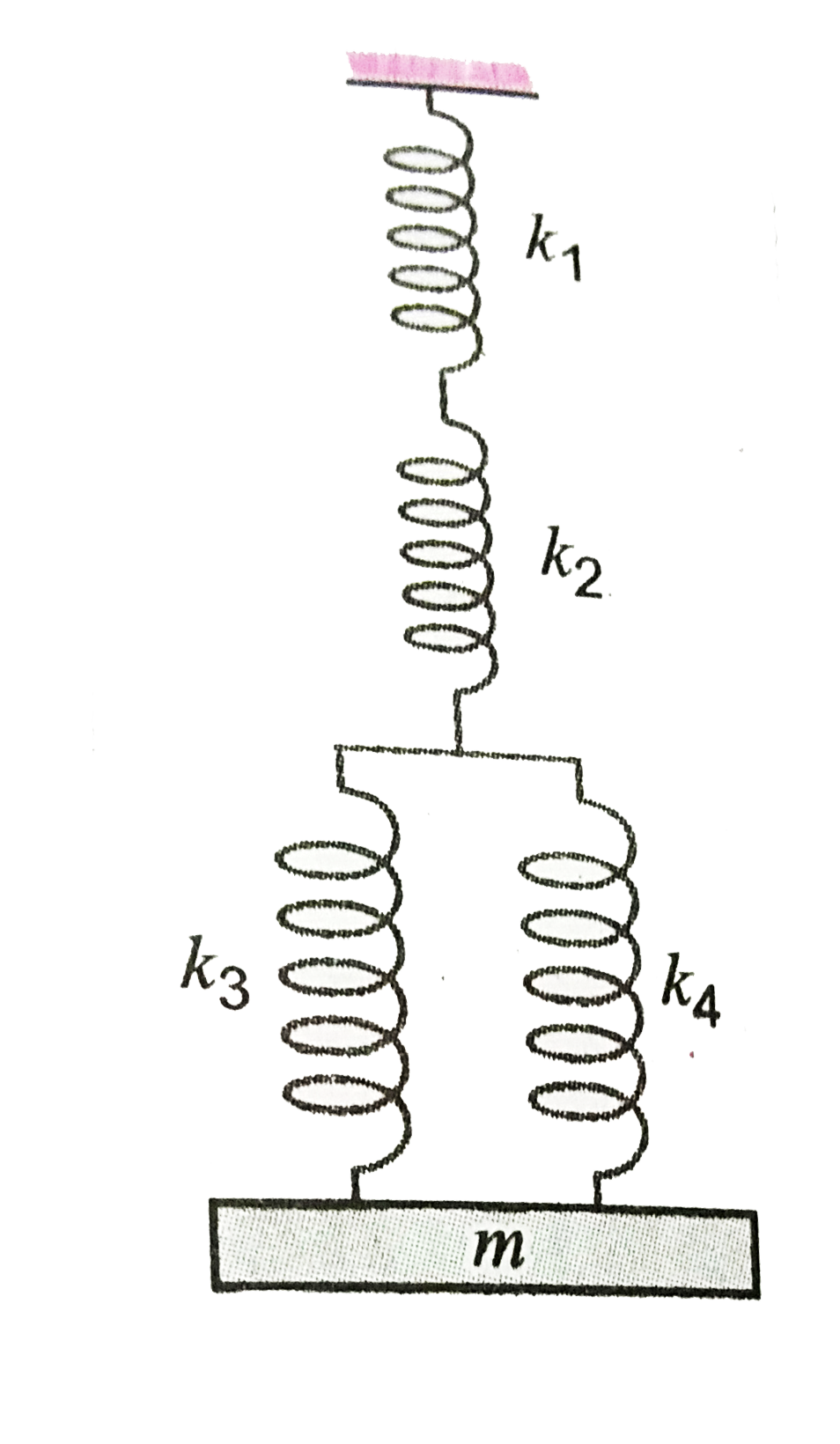
View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
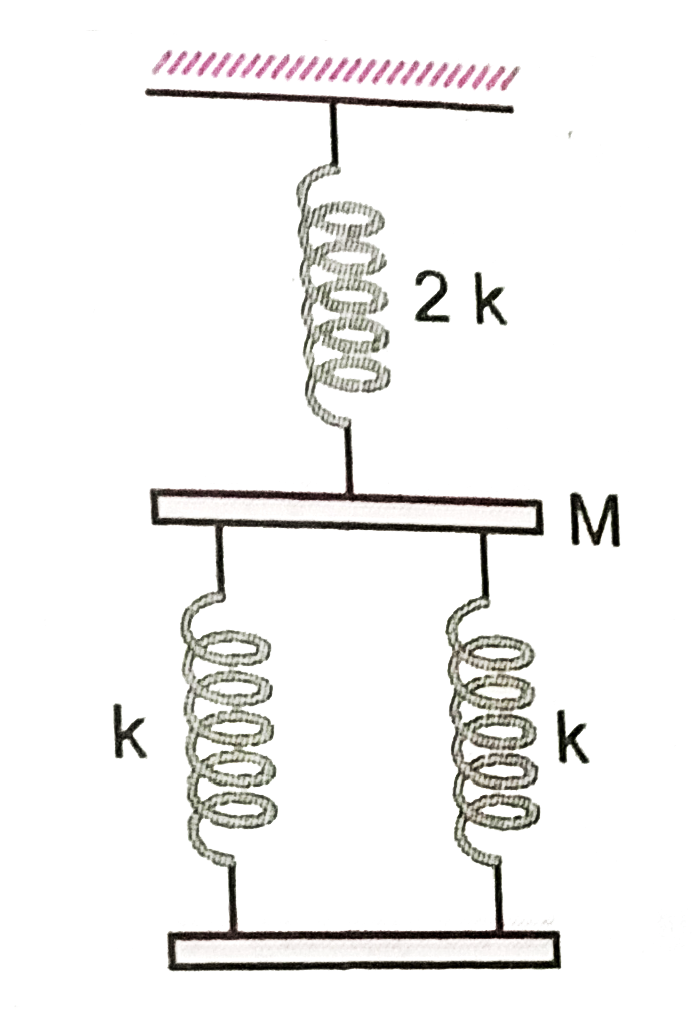
View SolutionThree spring are connected to a mass `m(=100g)` as shown in figure. Given `k=2.5Nm^(-1)`. (a) What is the effecitve spring constant of the combination of spring constant of the combination of springs? (b) When mass m oscillates, find time period of its vibration.
View SolutionTwo pendulums of length 90 cm and 100 cm start oscillating in phase. After how many osxillations will they b again in the same phase ?
View SolutionIf the acceleration due to gravity on the moon is one-sixth of that on the earth. What will be the change in length of a second pendulum there so that it may beat a second there? Take acceleration due to gravity on earth's surface `=9.8 ?`
View SolutionIf the length of a second's pendulum is increased by `1%` , how many seconds will it loss or gain in a day ?
View SolutionA simple pendulum has time period 2s in air. If the whole arrangement is placed in a non viscous liquid whose density is `1//2` times the density of bob, find the time period of oscillation in liquid.
View SolutionA second's pendulum is taken from a place where `g=9.8 ms^(-2)` to a place where `g=9.7 ms^(-2)` .How would its length be changed in order that its time period remains unaffected ?
View SolutionTwo pendulums of lengths 200 cm and 220.50 cm start oscillating in phase. After how many oscillations will they be in same phase for the first time ?
View SolutionTime period of is simple pendulum of length `L` is `T_(1)` and the point time peirod of a uniform rod of the same length `L` pivotal about one end and oscillating in vertical plane is `T_(2)`. Amplitude of oscillation in both the cased is small. The `T_(1)//T_(2)` is:
View SolutionA body is dropped in a hole drilled across diameter of the earth. Show that it executes SHM Asuume earth to be a homogenous sphere, find the time period of its motion. Given density of earth is `5.51 xx10^(3)Kgm^(-3)` and `G=6.67xx10^(-11)Nm^(2)kg^(-2)`
View SolutionA cylinderical wooden block of cross-section 15.0 `cm^(2)` and 250 gram attached to its bottom. The cylinder floats vertically. From the state of equilibrium, it is slightly depressed and released. If the specific gravity of wood is 0.3 and `g=9.8 ms^(-2)`, deduce the frequency of oscillation of the block.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA test tube weighing 10g and external dismeter 2.5cm is floated vertically in water by placing 20g of mercury at its bottom. The tube is depressed in water a little and then released. Find the time of oscillation. Take `g=10ms^(-2)`.
View SolutionA particle of mas 10g is placed in a potential field given by` U=(500x^(2)+100)` erg `//` gm. Calculate the frequency of oscillation.
View SolutionIn dampled oscillations, the amplitude of oscillatinos is reduced to one-fourth of its initial value 10cm at the end of 50 oscillations. What will be its amplitude when the oscillator completes 150 oscillations ?
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA body of mass `1kg` is suspended from a weightless spring having force constant `600N//m`. Another body of mass `0.5 kg` moving vertically upward hits the suspended body with a velocity of `3.0m//s` and get embedded in it. Find the frequency of oscillations and amplitude of motion.
View SolutionThe potential energy of a particle of mass `1kg` in motion along the x- axis is given by: `U = 4(1 - cos 2x)`, where `x` in meters. The period of small oscillation (in sec) is
View SolutionFor aluminium , the modulus of rigidity is `2.1xx10^(10)Nm^(-2` and density is `2.7xx10^(3)kg//m^(3)`.Find the speed of transverse waves in the medium.
View SolutionFor a steel rod, the Young's modulus of elasticity is `2.9xx10^(11)N//m^(2)`, and the density of steel is `8xx10^(3)kg//m^(3)`.What is the velocity of longitudinal waves in steel?
View SolutionAt normal temperature and pressur, 4g of He occupies a volume of 22.4 litre. Determine the speed of sound in helium. Take 1 atmospheric pressure `=10^(5)N//m^(2)` and `gamma` for helium `=1.67`.
View SolutionThe diameter of an iron wire is 1.20 mm. If the speed of transverse waves in the wire is `50.0m//s`, what is the tension in the wire? The density of iron is `7.7xx10^(3)kg//m^(3)`
View SolutionA source of sound is placed at one end of an iron bar 2 km long. Two sounds are heard at the other end at an interval of 5.6s. If the velocity of sound in air is `330m//s`, find the velocity of sound in iron.
View SolutionA body sends waves 100mm long through medium A and 0.25m long in medium B. If the velocity of waves in medium A is `80cms^(-1)`, calculate the velocity of waves in medium B.
View SolutionThe distance between two points on a stretched string is 20 cm. A pregressive wave of frequency 400 hertz travels on the string with a velocity of `100m//s`. Calculate phase differency between the points.
View SolutionA stone is dropped into a well in which water is 78.4m deep. After how long will the sound of splash be heard at the top ? Take velocity of sound in air `=332ms^(-1)`.
View SolutionFrom a cloud at an angle of `30^(@)` to the horizontal, we hear the thunder clap 8 s after seeing the lightening flash. What is the height of the cloud above the ground if the velocity of sound in air is `330 m//s` ?
View SolutionFor aluminium, the bulk modulus and modulus of rigidity are `7.5xx10^(10)N//m^(2) and 2.01xx10^(10)N//m^(2)` respectively. Find the velcoity of longitudinal and transverse wave in the medium. Given desity of aluminium is `2.7xx10^(3)kg//m^(3)`.
View SolutionA progressive wave of frequency 500Hz is travelling with a velocity of 360 m`//` s. How far part are two points `60^(@)` out of phase ?
View SolutionFind the ratio of velocity of sound in helium `(gamma =5//3)` and that in oxygne `(gamma=7//5)`. Given the molecular weights of Helium and Oxygen are 4 and 32 respectively.
View SolutionAt what temperature will the speed of sound in hydrogen be the same aas in oxygen at `100^(@)` ? Molar Masses of oxygen and hydrogen are in the ratio `16: 1` .
View SolutionA sound wave propagating in air has a frequency of 4000Hz. Calculate the percentage change in wavelength when the wavefront initially in a region where `T=27^(@)C` enters a region where temperature decreases to `10^(@)C`.
View SolutionA gas is a mixture of two parts by volume of hyprogen and part by volume of nitrogen at `STP`. If the velocity of sound in hydrogen at `0^(@) C` is `1300 m//s` . Find the velocity of sound in the gaseous mixure at `27^(@)C`.
View SolutionA tuning fork of frequency 220Hz produces sound waves of wavelength 1.5m in air at NTP. Calculate the increase in wavelength, when temperature of air in `27^(@)C`.
View SolutionThe speed of sond in air is `332m//s` at NTP. What will be its value in hydrogen at NTP, if density of hydrogen at NTP is `1//16th` that of air ?
View SolutionA steel wire has a length os 12.0m and a mass of 2.10 kg. What should be the tension in the wire at `20^(@)C` so that speed of transverse wave on the wire equals the speed of transverse wave on the wire equals the speed of sound in dry air at this temperature which is `330ms^(-1)` ?
View SolutionAt what temperature, velocity of sound in oxygen is same as that in nitrogen at `10^(@)C`? Given their densities at `0^(@)C` are in the ratio `16:`4`.
View SolutionIf velocity fo sound in hydrogen at `0^(@)C` is `1280 ms^(-1)` , what will be the velocity of sound at the same temperature in a mixture, 2 parts in volume of hydrogen to one part of oxygen. Density of oxygen is 16 times that of hydrogne.
View SolutionA tuning fork of frequency 220Hz produces sound waves of wavelength 1.5m in air at NTP. Calculate the increase in wavelength, when temperature of air in `27^(@)C`.
View SolutionWrite the equation of a progressive wave propagating along the positive x-direction, whose amplitude is 5cm, frequency 250Hz and velocity 500 m`//` s.
View SolutionThe speed of a wave in a stretched string is `20ms^(-1)` and its frequency is 50Hz. Calculate the phase difference in radian between two points situated at a distance of 5 cm on the string ?
View SolutionA wave travelling along a string is given by `y(x,t)=0.05 sin (40x-5t)`, in which numerical constants are in SI units. Calculate the displacement at distance 35 cm from origin, and time 10 sec.
View SolutionA simple harmonic wave is expressed by equation,
`y=7xx10^(-6)sin(800pit-(pi)/(42.5)x)`
where y and x are in cm and t is in second.
Calculate (i) amplitude (ii) frequency
(iii) wavelength )
(iv) wave velocity
(v) Phase difference between two particles separated by 17.0cm.
View SolutionThe equation of a transverse wave travelling along the X-axis is givey by
`xi=10 sin pi(0.01x-2.00t)`
where `xi` and x are expressed in cm and t in sec. Find the amplitude, frequency, velocity and wavelength of the wave.
View SolutionA simple harmonic wave has the equation,
`xi=0.5 sin (314t-1.57x)`
where t, x and `xi` are in second, metre and centimetres respectively. Find the frequency and wevelength of this wave. Another wave has the equation
`xi=0.1 sin (314t-1.57x+1.57)`
Deduce the phase difference and ratio of intensities for the above two waves.
View SolutionThe equation for a wave travelling in x-direction on a string is `y =(3.0cm)sin[(3.14 cm^(-1) x - (314s^(-1))t]` (a) Find the maximum velocity of a particle of the string. (b) Find the acceleration of a particle at x =6.0 cm at time t = 0.11 s.
View SolutionWrite down the equation for a wave propagating with velocity `330m//s` and having frequency 110Hz. The amplitude is 0.05m.`
View SolutionThe equation of a travelling wave is
`y=0.07sin (12pix-500pit)`
where the distances are in metre and time is in second. Calculate the wavelength and velocity of wave.
View SolutionA displacement wave is represented by
`xi=0.25xx10^(-3)sin(500t-0.025x)`
Deduce (i) amplitude (ii) period (iii) angular frequency (iv)wavelength (v) amplitude of particle velocity (vi) amplitude of particle acceleration . `xi`, t and x are in cm, sec, and metre respectively.
View SolutionA simple harmonic travelling wave is represented by `y=50sinpi(20t-0.08x)` is SI units. Find its amplitude, time period and wavelength. Also, calculate maximum particle velocity.
View SolutionThe vibrations of a string of length `60cm` fixed at both ends are represented by the equation----------------------------
`y = 4 sin ((pix)/(15)) cos (96 pit)`
Where `x` and `y` are in `cm` and `t` in seconds.
(i) What is the maximum displacement of a point at `x = 5cm`?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at `x = 7.5 cm` at `t = 0.25 sec`.?
(iv) Write down the equations of the component waves whose superpositions gives the above wave.
View SolutionThe consitutent waves of a stationary wave on a string fixed at two ends are amplitude 6 cm, frequency 50Hz and velocity `80cms^(-1)`. Write down the equation of stationary wave.
View SolutionWhat are the three lowest frequencies for standing waves on a wire 10m long having a mass of 100g, which is stretched under a tension of 1600N?
View SolutionThe standing waves are set up by the superimposition of two waves:
`y_(1)=0.05 sin (15pit-x)`and
`y_(2)=0.05 sin (15pit+x)`, where x and y are in metre and t in seconds. Find the displacement of particle at `x=0.5m.`
View SolutionThe mass of 1m long steel wire is 20 g. The wire is stretched under a tension of 800N. What are the frequencies of fundamental mode of vibration and next two higher modes ?
View SolutionA string vibrates with a frequency of 200Hz. Its length iss doubled and its tension is altered till it begins to vibrate with a frequency of 300Hz. What is the ratio of new tension to the original tension ?
View SolutionA metal wire of linear mass density of `9.8g//m` is stretched with a tension of `10 kg-wt` between two rigid support `1meter` apart. The wire passes at its middle point between the poles of a permanent magnet, and it vibrates in resonance when carrying an alternating current of frequency `n`. the frequency `n` of the alternating source is
View SolutionThe length of a sonometer wire is `0.75m`, and density `9xx10^(3)m`. It can bear a stress of `8.1xx10^(8)N//m^(2)` without exceeding the elastice limit. What is the fundamental frequency that can be produced in the wire?
View Solution
PROBLEMS FOR PRACTICE questions and complete solutions for chapter OSCILLATIONS AND WAVES of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS OSCILLATIONS AND WAVES
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- conceptual problems
- CURIOSITY QUESTION
- Fill In The Blanks
- Higher Order Thinking Skills
- integer type question
- JEE mains adv..(multiple choice quection)
- Long Answer Questions
- Multiple Choice Question
- Multiple Choice Question-I
- Multiple Choice Question-II
- multiple choice Questions
- NCERT CHAPTER
- NCERT EXERCISES WITH SOLUTIONS
- PROBLEMS FOR PRACTICE
- SAMPLE PROBLEM
- Short Answer Questions
- SOLVED EXAMPLES
- Value Based Questions
- Very Short Answer Questions