Complete Solutions to NCERT EXERCISES WITH SOLUTIONS of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| PRADEEP | NCERT EXERCISES WITH SOLUTIONS |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Which of the following examples represent periodic motion?
(a) A swimmer completing one (return0trip from one bank of a river to other bank. (b) A freely suspended bar megnet displaced from its `N-S` direction and released. (c) A hydrogen molecule rotating about its centre of mass. (d) An arrow released from a bow.
View SolutionWhich of the following examples examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position.
View SolutionFig. 14.23 depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion) ?

View SolutionWhich of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic , and (c) non-periodic motion ? Give period for each case of periodic motion `, omega` is any positive constant). ltbr. (a) `sinomegat-cosomegat)` (b) `sin^(3)omegat` (c) `3cos((pi)/(4)-2omegat)`
(d) `cosomegat+cos3omegat+cos5omegat)` (e) ` exp(-omega^(2)t^(2))` (f) `1+omegat+omega^(2)t^(2)`
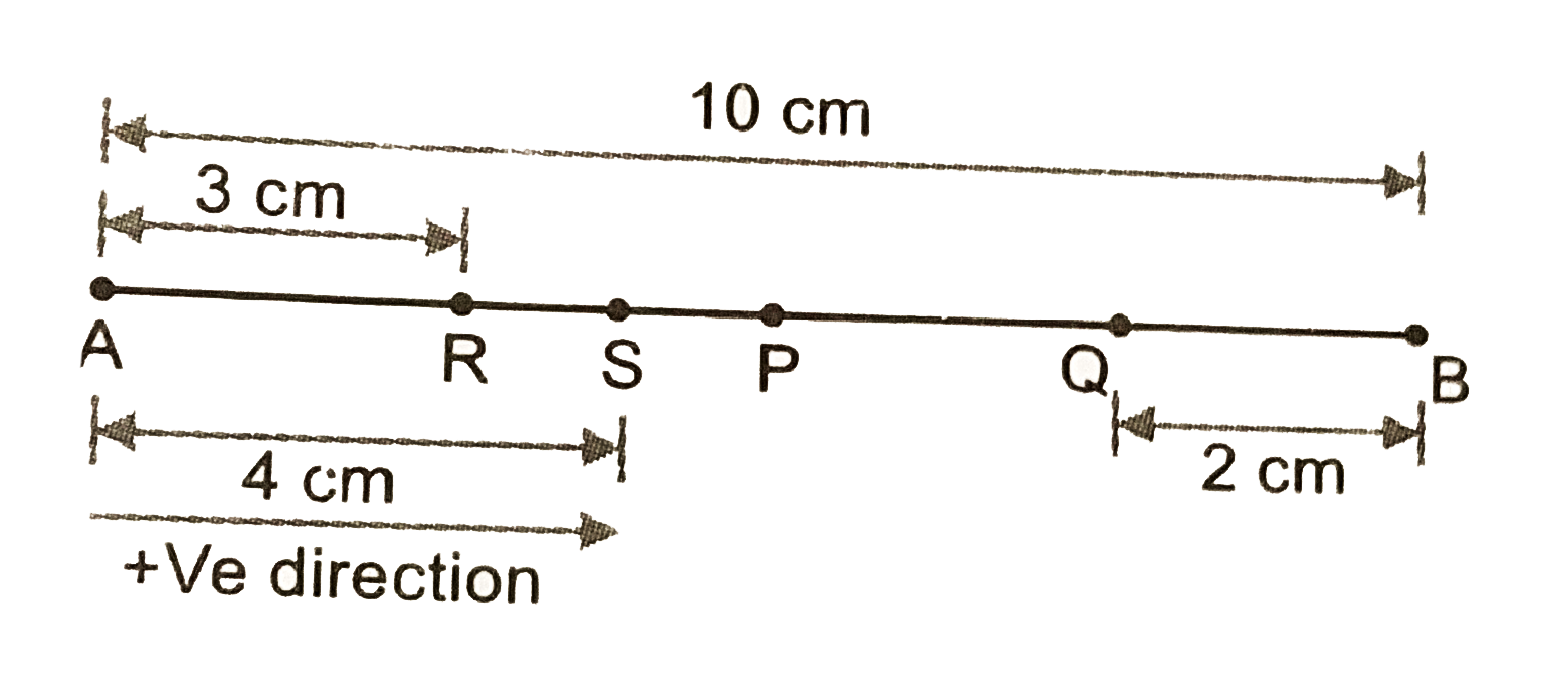
View SolutionA particle is in linear S.H.M. between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is.
(a) at the end (A) at the end B,
(c) at the mid point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A goiing towards B, and
(f) at 4 cm away from A going towards A.
View SolutionWhich of the following relationship between the acceleration, a and the displacement x of a particle involve simple harmonic motion.
(a) `a=7.0x` (b) `a=-200x^(2)` (c) `a=-10x` (d) `a=100x^(3)`
View SolutionThe motion of a particle in S.H.M. is described by the displacement function, `x=Acos(omegat+phi)`, If the initial `(t=0)` position of the particle is 1cm and its initial velocity is `omega cm s^(-1)`, what are its amplitude and initial phase angle ? The angular frequency of the particle is `pis^(-1)`. If instead of the cosine function, we choos the sine function to describe the SHM`: x=B sin(omegat+alpha)`, what are the amlitude and intial phase of the particle with the above intial conditions ?
View SolutionA spring balance has a scale that reads from 0 to 50kg. The length of the scale is 20cm. A body suspended from this spring, when displaced and released, oscillates with period of 0.60s. What is the weight of the body?
View SolutionA spring of force constant `1200Nm^(-1)` is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionIn example 34, let us take the position of the mass, when the spring is unstretched, as x=0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass, if at the moment we start the stop watch (t=0), the mass is (i) at the mean position (ii) at the maximum stretched position (iii) at the maximum compressed position.
In what do these different functions of SHM differ ? Frequency, amplitude or initial phase ?
View SolutionFigures,. Correspond to two circular motions. The radius of the circle, the peirod of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each. Obtain the corresponding equations of simple harmonic motions of the revolving particle P in each case.
View SolutionPlot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial`(t=0)` position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case `: (x` is in cm and t is in s ).
(a) `x=-2 sin(3t+pi//3)` (b)`x=cos(pi//6-t)` (c) `x=3sin(2pit+pi//4)` (d) `x=2cospit`
View Solutionspring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionThe piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0m. If the piston moves with simple harmonic motion with an angular frequency of `200rev//`min., what is its maximum speed ?
View SolutionThe acceleration due to gravity on the surface of the moon is `1.7ms^(-2)`. What is the time perioid of a simple pendulum on the surface of the moon, if its time period on the surface of earth is `3.5s ?` Take `g=9.8ms^(-2)` on the surface of the earth.
View SolutionAnswer the following questions: (a) Time period of particle is S.H.M. depends on the force constant k and mass m of the particle `: T=2pisqrt(m//k).` A simple pendulum executes S.H.M. approximately. Why then is the time-period of a pendulum independent of the mass of the pendulum?
(b) The motino of simple pendulum is approximatley simple harmonic for small angles of oscillation. For large angle of oscillation, a more involved analysis (beyond the scope of this book) shows that T is greater that `2pisqrt(l//g)`. Think of a quanlitative argument to appreciate this result.
(c) A man with a wrist watch on his hand falls from the top of tower. Does the watch give correct time during the free fall?
(d) What is teh frequency of oscillation of a simple pendulum mounted iin a cabin that is freely falling under gravity?
View SolutionA simple pendulum of length l and having a bob of mass M is suspended ina car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium, what will be its time period ?
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density `rho_(1)`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T=2pisqrt((hrho)/(rho_(1)g))`
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
NCERT EXERCISES WITH SOLUTIONS questions and complete solutions for chapter OSCILLATIONS AND WAVES of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS OSCILLATIONS AND WAVES
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- conceptual problems
- CURIOSITY QUESTION
- Fill In The Blanks
- Higher Order Thinking Skills
- integer type question
- JEE mains adv..(multiple choice quection)
- Long Answer Questions
- Multiple Choice Question
- Multiple Choice Question-I
- Multiple Choice Question-II
- multiple choice Questions
- NCERT CHAPTER
- NCERT EXERCISES WITH SOLUTIONS
- PROBLEMS FOR PRACTICE
- SAMPLE PROBLEM
- Short Answer Questions
- SOLVED EXAMPLES
- Value Based Questions
- Very Short Answer Questions