Complete Solutions to JEE mains adv..(multiple choice quection) of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| PRADEEP | JEE mains adv..(multiple choice quection) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
when two displacements represented by `y_(1) = a sin(omega t)` and `y_(2) = b cos (omega t)` are superimposed the motion is
View SolutionA particle is moving in SHM in a straight line. When the distance of the particle from equilibrium position has values `x_(1)` and `x_(2)` , the corresponding values of velocities are `u_(1)` and `u_(2)`. Show that time period of vibration is `T=2pi[(x_(2)^(2)-x_(1)^(2))/(u_(1)^(2)-u_(2)^(2))]^(1//2)`
View SolutionThe oscillationof a body on a smooth horizontal surface is represented by the equation
`x=Acos omegat`
where `x=` displacement at time t, `omega=` frequency of oscillation. Which one of the following graphs shows correctly the variation of acceleration a with time t ?
View SolutionA particle performs harmonic oscillations along a straight line with a period of 6s and amplitude 4 cm. The mean velocity of the particle averaged over the time interval during which it travels a distance of 2 cm starting from the extreme position is
View SolutionA particle performs simple harmonic mition with amplitude A. Its speed is trebled at the instant that it is at a destance
`(2A)/3` from equilibrium position. The new amplitude of the motion is:
View SolutionTwo pendulums of time period 3 s and 8 s respectively starts oscillating simultaneously from two oppositee extreme positions. After how much time they will be in the same phase ?
View SolutionA particle executies linear simple harmonic motion with an amplitude `3cm` .When the particle is at `2cm` from the mean position , the magnitude of its velocity is equal to that of acceleration .The its time period in seconds is
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is `V(x) = k|x|^3` where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe density `rho` of a liquid varies with depth h from the free surface as `rho=kh`. A small body of density `rho_(1)` is released from the surface of liquid. The body will
View SolutionA mass m is performing linear simple harmonic motion, then which of the following graph represents correctly the variation of acceleration a corresponding to linear velocity `upsilon` ?
View SolutionA particle executing `SHM` while moving from start it found at distance `x_(1) x_(2)` and `x_(2)` from comes at the and of three successive second The period of oscillation is
where `theta = cos^(-1)((x_1 + x_2)/(2x_(2)))`
View SolutionThe acceleration versus displacement graph of a particle performing SHM is shown in figure. The time period of oscillation of particle in second is

View SolutionIf displacement `x` and velocity `v` related as
`4v^(2) = 25 - x^(2)m` in a `SHM` Then time period of given `SHM` is (consider SI unit)
View SolutionThe velocity v and displacement x of a particle executing simple harmonic motion are related as
`v (dv)/(dx)= -omega^2 x`.
`At x=0, v=v_0.` Find the velocity v when the displacement becomes x.
View SolutionThe (x - t) graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at `t = 4//3 s` is
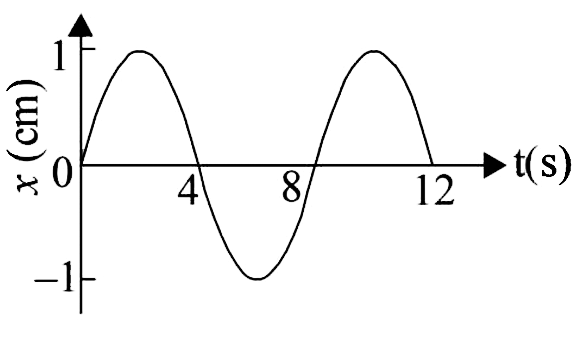 .
.
View SolutionIf x, and a denote the displacement, the velocity and the acceler of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View SolutionTwo simple harmonic motion are represented by equations
`y_(1) = 4 sin (10 t + phi) rArr y_(2) = 5 cos 10t`
What is the phase difference between their velocities ?
View SolutionTwo particles execute simple harmonic motion of same amplitude and frequency along the same straight line. They pass on another, when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
View SolutionA particle executes SHM of period 1.2s and amplitude 8 cm. Find the time it takes to travel 13 cm from the positively extremily of its oscillation `cos^(-1)0.625=51^(@)`
View SolutionA particle is performing simple harmonic motion along `x-`axis with amplitude `4 cm` and time period `1.2 sec` .The minimum time taken by the particle to move from `x = 2 cm to x = +4 cm` and back again is given by
View SolutionA particle executes simple harmonic motion between `x = -A and x = + A`. The time taken for it to go from `0 to A//2 is T_1 and to go from A//2 to (A) is (T_2)`. Then.
View SolutionThe period of a particle in SHM is `8s`. At `t=0` it is at the mean position. The ratio of the distances travled by it in the first and the second second is
View SolutionA partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM.
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency `omega` along the x-axis . Their mean position is separated by distance `X_(0)(X_(0)gtA). If the maximum separation between them is (X_(0)+A), the phase difference between their motion is:
View SolutionA particle is subjected to two mutually perpendicular simple harmonic motions such that its `X` and `y` coordinates are given by `X=2 sin omegat` , `y=2 sin (omega+(pi)/(4))`
The path of the particle will be:
View SolutionA particle moves with simple harmonic motion in a straight line. In first `taus`, after starting form rest it travels a destance a, and in next `tau s` it travels 2a, in same direction, then:
View SolutionTwo pearticle are oscillation along two close parallel straght lines side by side with the same frequency and amplitude They pass each other moving in opposite directions when their displacement is half of the on a stright line perpendicular to the part of the two particle The phase difference is
View SolutionTwo simple harmonic motions act on a particle. These harmonic motions are
`x=Acos (omegat+delta), y=Acos (omegat+alpha)`
When `delta=alpha+(pi)/(20,` the resulting motion is
View SolutionThe displacement `y` of a particle executing periodic motion is given by `y = 4 cos^(2) ((1)/(2)t) sin(1000t)`
This expression may be considereed to be a result of the superposition of
View SolutionFour simple harmonic motions`, c_(1)=8sinomegat,x_(2)=6sin(omegat=pi//2) , x_(3)=4sin(omegat+pi) and x_(4)=2sin (omegat+3pi//2)` are superimposed on each other. The resuslting amplitude and its phase difference with `x_(1)` are respectively
View SolutionTwo particles P and Q are executing SHM across same straight line whose equations are given as `y_(P)=Asin (omegat+phi_(1)) and y_(Q)=Acos (omegat+phi_(2))`
An observer, at `t=0` observer the particle P at a distance `A//sqrt(2)` moving to the right from mean position O while particle Q at `(sqrt(3))/(2)` A moving to the left from mean position O as shown in figure. Then `phi_(2)-phi_(1)(i n rad)` ie equal to

View SolutionThe displacement equation of a particle is `x=3 sin 2t+4cos2t`. The amplitude and maximum velocity will be respectively
View SolutionA particle of mass 5 kg is placed in a field of gravitational potential
`v=(7x^(2)-21x)J//kg` . Then its motion
View SolutionA particle of mass 2 kg moving along x-axis has potential energy given by, `U=16x^(2)-32x` ( in joule), where x is in metre. Its speed when passing through `x=1 is 2ms^(-1)`
View SolutionThe function `sin^(4)(omegat)` represents
View SolutionA point mass is subjected to two simultaneous sinusoidal displacements in `x - direction, x_1 (t) = A sin (omega)t and x_2 (t) = A sin ((omega t + (2 pi)/(3))`. Adding a third sinusoidal displacement `x _3 (t) = B sin (omega t + phi)` brings the mas to a complete rest. The values of (B) and (phi) are.
View SolutionOut of the following function reporesenting motion of a particle which represent `SHM`
(i) ` y = sin omega t - cos omega t `
(ii) `y = sin^(3) omega t`
(iii)`y =5cos ((3pi)/(4) - 3omega t)`
(iv) ` y = 1+ omega t + omega^(2) t^(2) `
View SolutionA particle is executing simple harmonic motion with a time period `T`. At time `t=0,` it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
View SolutionA body is executing simple harmonic motion. At a displacement `x` its potential energy is `E_(1)` and at a displacement `y` its potential energy is `E_(2)` The potential energy `E` at displacement `(x+y)` is
View SolutionFor a simple pendulum, a graph is plotted its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?
View SolutionA solid cube of side a and density `rho_(0)` floats on the surface of a liquid of density `rho`. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA pendulum bob has a speed 3m/s while passing thorugh its lowest position. What is its speed when it makes an angle of `60^0` with the vertical? The length of the pendulum is 0.5m Take `g=10 m/s^2`.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass `M`. The piston and the cylinder have equal cross-sectional area `A`. When the piston is in equilibrium, the volum of the gas is `V_(0)` and its pressur is `P_(0)`. The pistong is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionA simple pendulum is oscillating without damiping, When the displacement of the bob is less than maximum, its acceleration vector `veca` is correctly show in:
View SolutionThere is a rod of length `l` and mass `m`. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionTwo simple pendulums have time period `T` and `5T//4`. They start vibrating at the same instant from the mean position in the same phase. The phase difference (in rad) between them when the smaller pendulum completes one oscillation will be
View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation `y = K t^2, (K = 1 m//s^2)` where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of `(T_1^2)/(T_2^2)` is `(g = 10 m//s^2)`.
View SolutionA simple pendulum of length `L ` is suspended from the top of a flat beam of thickness `L//2` . The bob is pulled away from the beam so that it makes an angle `thetalt30^(@)` with the vertical , as shown in figure. It is then released from rest. If `phi` is the maximum angular deflection to teh right, then
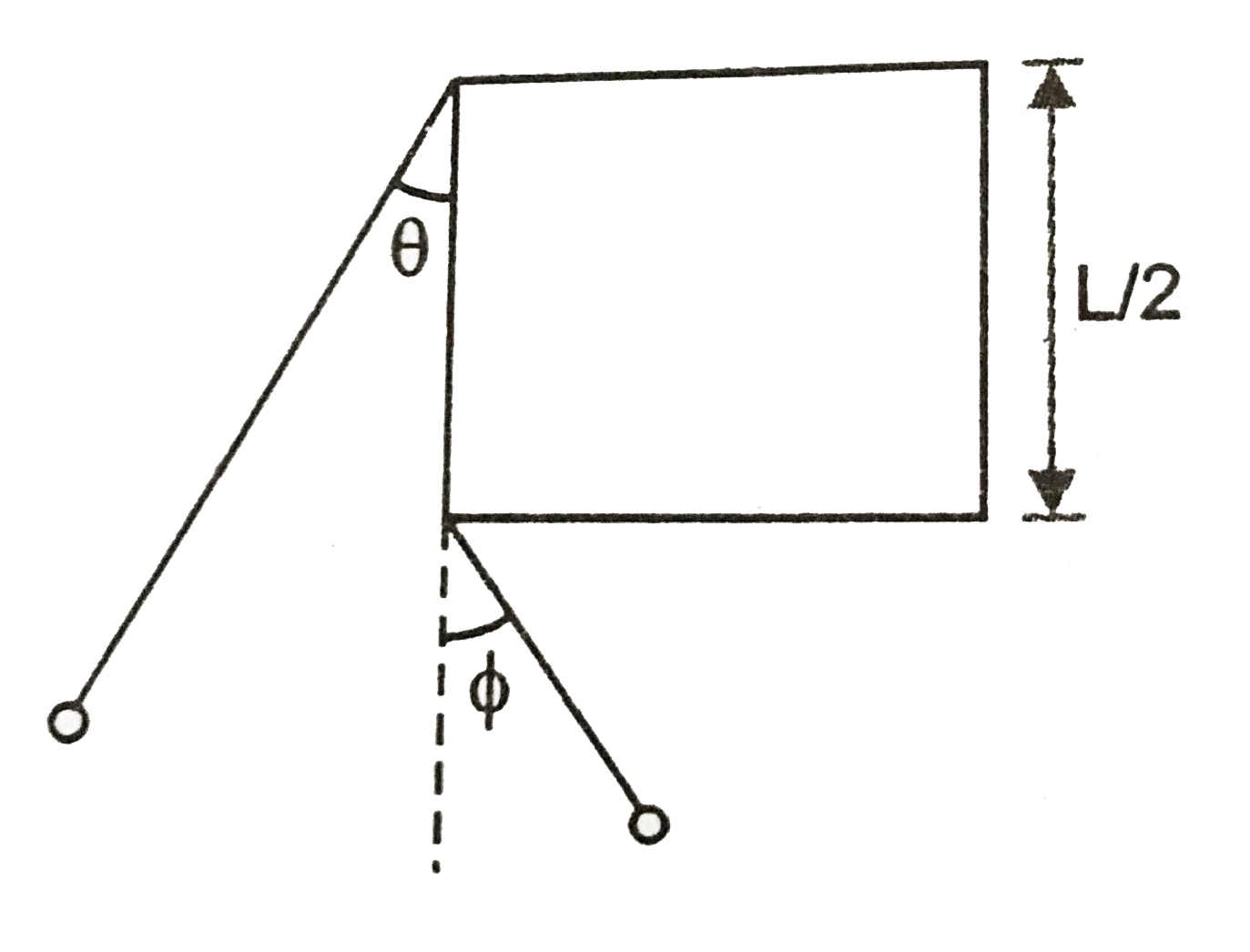
View SolutionA pendulum suspended from the roof of an elevator at rest has a time period `T_(1)`, when the elevatore moves up with an acceleration `a` its time period becomes `T_(2)`, when the elevator moves down with an acceleration `a`, its time period becomes `T_(3)`, then
View SolutionA spring of force constant `k` is cut into lengths of ratio `1 : 2 : 3`. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k'. Then k' : k" is :
View SolutionThree springs are connected to a mass m as shown in figure, When mass oscillates, what is the effective spring constant and time period of vibration? Given `k=2Nm^(-1)` and m=80 gram.
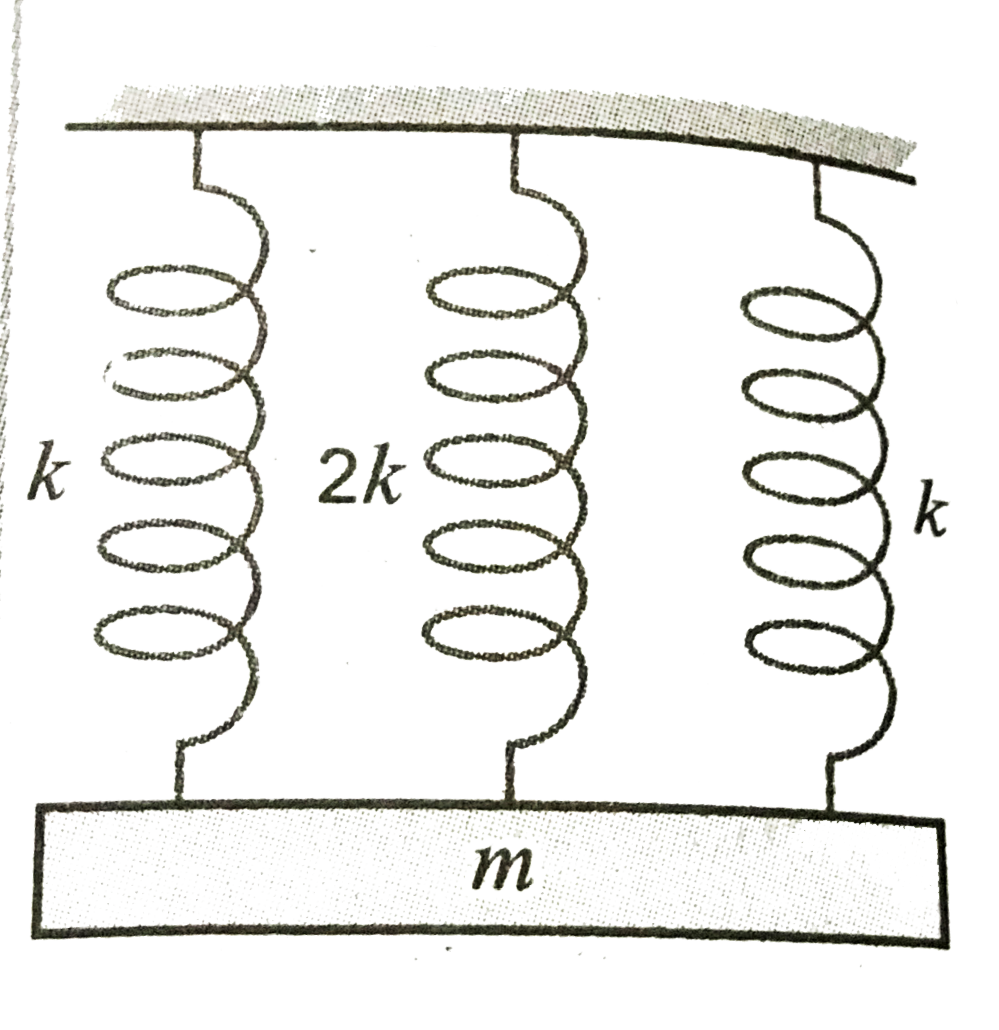
View SolutionA force of `6.4N` streches a vertical spring by `0.1m` The mass that must be supended from the spring so that it oscilation with a time period of `pi//4` second
View SolutionA body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
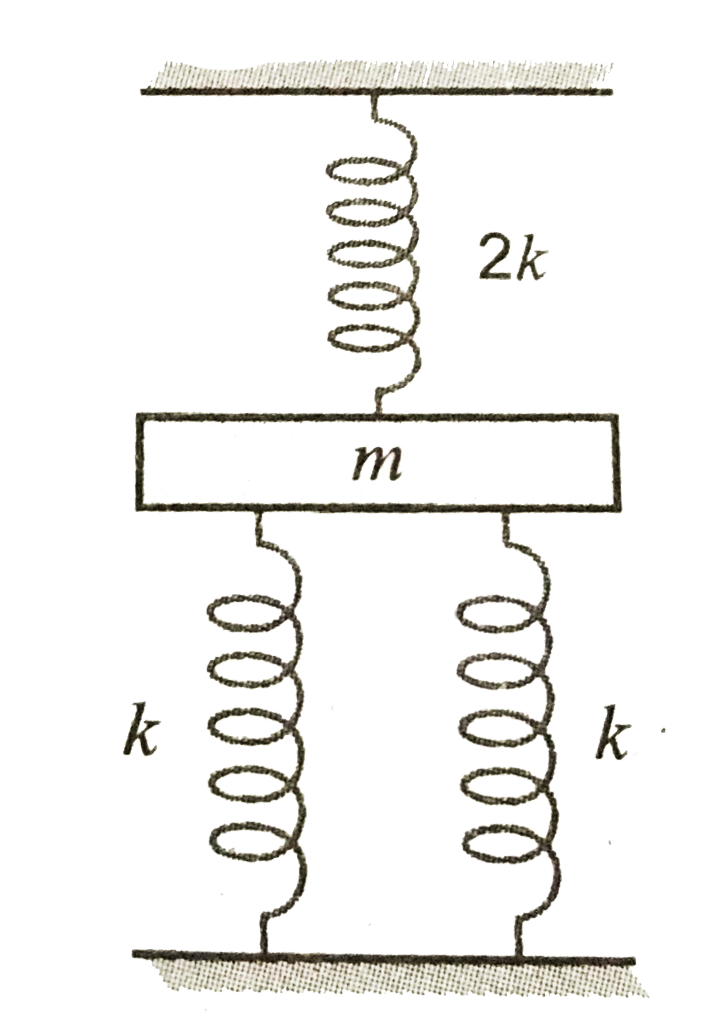
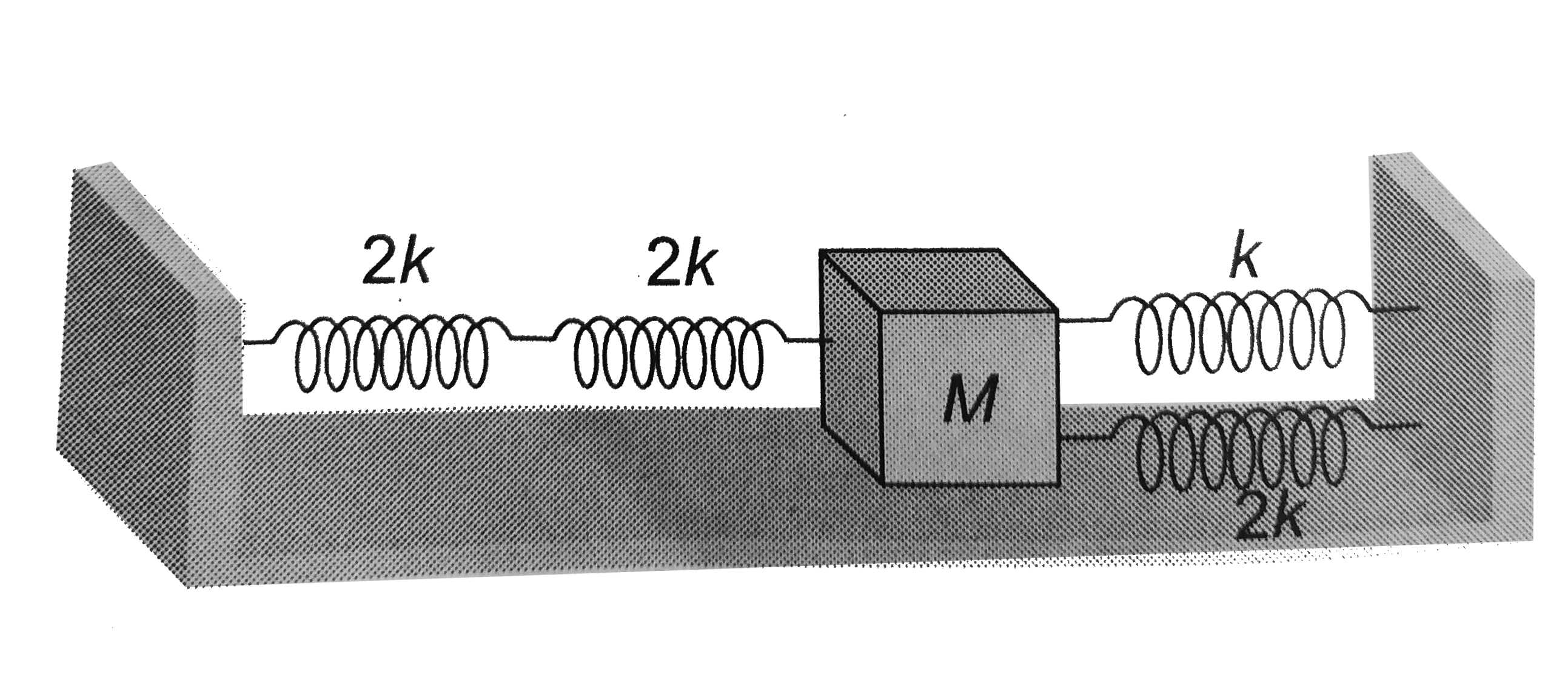
View SolutionFour mass less spring whose force constant are `2k , 2k, k` and `2k` respectively are attached to a mass `M` kept on a friction less plate (as shown in figure) if the mass `M` is displaced in the horizontal direction then the frequency of oscillation of the system is
View SolutionA particle of mass `m` is fixed to one end of a massless spring of spring constant `k` and natural length `l_(0)`. The system is rotated about the other end of the spring with an angular velocity `omega` ub gravity-free space. The final length of spring is
View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

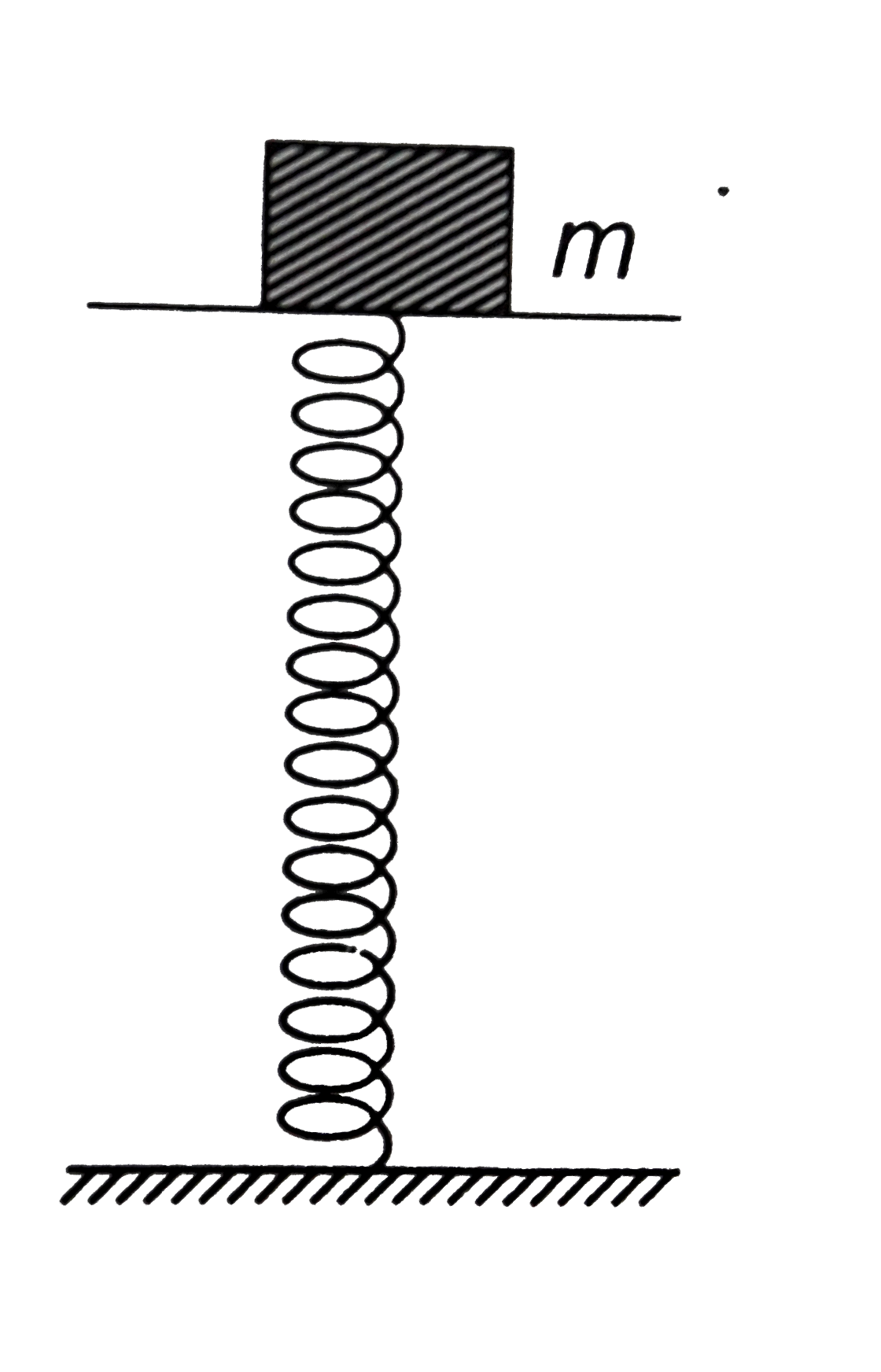
View SolutionA mass of `2.0 kg` is put on a flat pan attached to a vertical spring fixed on the ground as shown in figure. The mass of the spring and the pan is negligible. When pressed slightly and realeased the mass executes a simple contant is `200 N//m`. What should be the minimum amplitude of the motion, so that the mass gets the detached from the pan? `(Take g= 10 m//s^(2))`
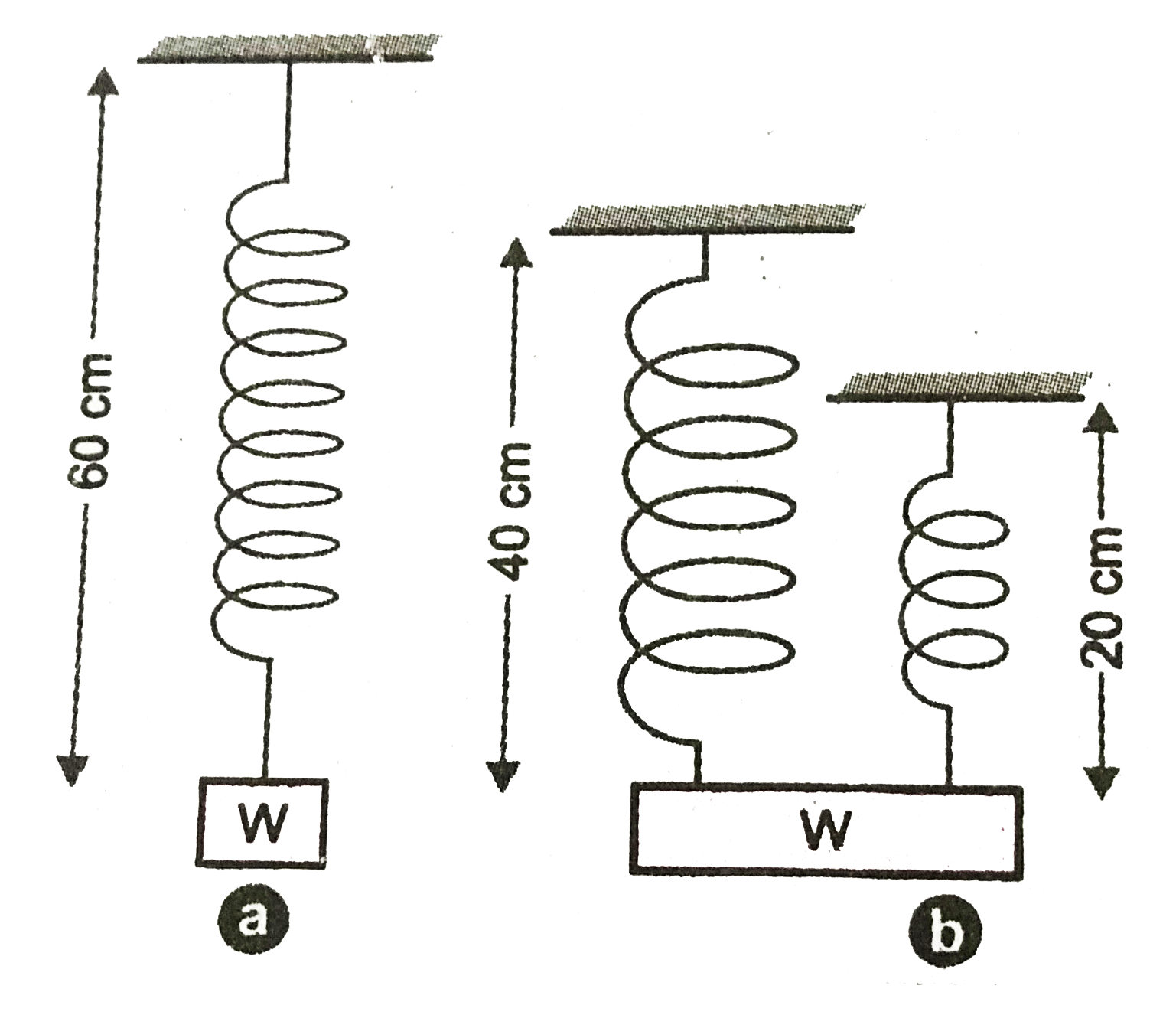
View SolutionA block of weight `W` produces an extension of `9cm` when it is hung by an elastic spring of length of `60cm` and is in equilibrium. The spring is cut into two parts, one of length `40cm` and the other of length `20cm`. The same load `W` hangs in equilibrium supported by both parts as shwon in figure. The extension in `cm` noe is
View SolutionTwo springs, of spring constants `k_(1)` and `K_(2)`, have equal highest velocities, when executing SHM. Then, the ration of their amplitudes (given their masses are in the ratio `1:2`) will be
View SolutionA uniform rod of length (L) and mass (M) is pivoted at the centre. Its two ends are attached to two springs of equal spring constants (k). The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle (theta) in one direction and released. The frequency of oscillation is. ?
 .
.
View SolutionThe mass (M) shown in the figure oscillates in simple harmonic motion with amplitude of the point (P) is.
 .
.
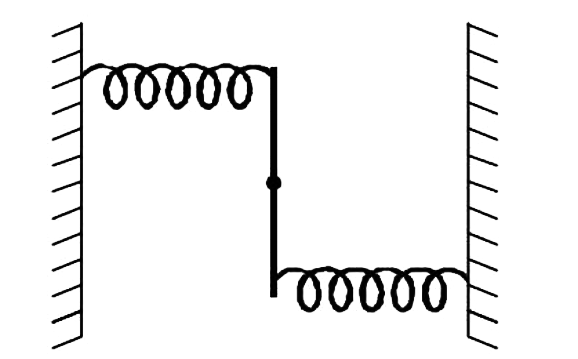
View SolutionA particle of mass `m` is attached to three identical springs of spring constant `k` as shwon in figure. The time period of vertical oscillation of the particle is

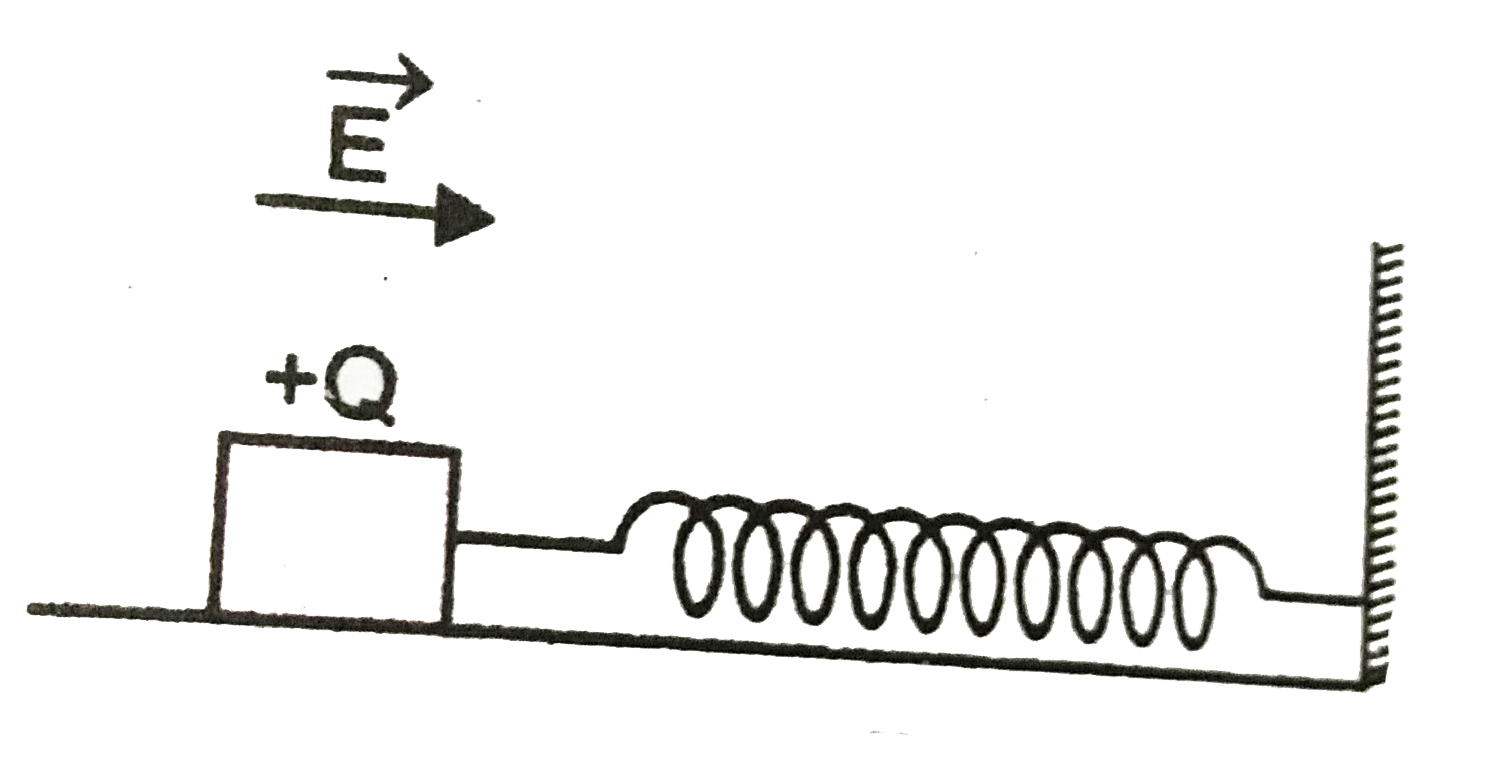
View SolutionA wooden block performs SHM on a frictionless surface with frequency, `v_(0)`. The block carries a charge `+Q` on its surface. If now a uniform electric field `vec (E)` is switched on as shwon in figure., then the SHM of the block will be
View SolutionA mass `M` attached to a horizontal spring executes `SHM` with an amplitude `A_(1)`. When mass `M` passes through its mean position a smaller mass `m` is placed over it and both of them move togther with amplitude `A_(2)`. Ratio of `((A_(1))/(A_(2)))` is:
View SolutionIf a spring of stiffness `'k'` is cut into two parts `'A'` and `'B'` of length `l_(A):l_(B)=2:3`, then the stiffness of spring `'A'` is given by
View SolutionA particle, with restoring force proportional to displacement and resulting force proportional to velocity is subjected to a force `F sin omega t`. If the amplitude of the particle is maximum for `omega = omega_(1)`, and the energy of the particle is maximum for `omega=omega_(2)`, then
View SolutionThe amplitude of a damped oscillator decreases to `0/9` times ist oringinal magnitude in `5s`, In anothet `10s` it will decrease to a times its original magnitude, wherea eqcrease .
View SolutionIf a simple pendulum has significant amplitude (up to a factor of1//e of original) only in the period between `t-0s to t=tau s`, then `tau` may be called the average life of the pendulum. When the sphetical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with b as the constant of propotional to average life time of the pendulum is (assuming damping is small) in seconds:
View SolutionA wave in a string has an amplitude of `2 cm`. The wave travels in the `+ve` direction of x axis with a speed of 1`28 ms^-1` and it is noted that `5` complete waves fit in `4 m` length of the string. The equation describing the wave is
View SolutionWhen a wave travels in a medium, th eparticle displacement is given by the equation
`y=asin 2pi(bt-cx), ` where `a,b` and `c` are constants. The maximum particle velocity will be twice the wave velocity. If
View Solution`4.0 g` of a gas occupies `22.4` litres at NTP. The specific heat capacity of the gas at constant volume is `5.0 JK^(-1)mol^(-1)`. If the speed of sound in this gas at NTP is `952 ms^(-1)`. Then the heat capacity at constant pressure is
View SolutionIf the intensity increased by a factor of 20, byhow may decibels is the sound level increased?
View SolutionFour harmonic waves of equal freuencies and equal intensity `I_(0)` have phase angles `0, (pi)/(3), (2pi)/(3)` and `pi`. When they are superposed, the intensity of the resulting wave is `nI_(0)`. The value of `n` is
View SolutionThe amplitude of a wave disturbance propagating in the positive x-direction is given by `y = (1)/((1 + x))^(2)` at time `t = 0` and by `y = (1)/([1+(x - 1)^(2)])` at `t = 2 seconds`, `x and y` are in meters. The shape of the wave disturbance does not change during the propagation. The velocity of the wave is ............... m//s`.
View SolutionIf the equation of progressive wave is given by `y=4 sin pi[(t)/(5)-(x)/(9)+(pi)/(6)]` then, which of the following is correct `?` (Assume SI units )
View SolutionA wave is represented by the equation `y=(0.001mm)sin[(50s^-10t+(2.0m^-1)x]`
View SolutionIn a sinusoidal wave the time required for a particular point to move from equilibrium position to maximum displacement is `0.17s`, then the frequency of wave is:
View SolutionSounds waves travel at `350m//s` through a warm air and at `3500m//s` through brass. The wavelength of a `700 Hz`. Acoustic wave as it enters brass from warm air
View SolutionA wave, `y_( `(x, t)`)=0.03 sin pi(2t-0.01x)` tavels in a medium. Here, `x` is in metre. The instantaneous phase differenc ( in rad) between the two point separated by `25cm` is
View SolutionA transverse wave is represented by the equation
`y=y_0sin.(2pi)/(lamda)(vt-x)`
For what value of `lamda`, the maximum particle velocity equal to two times the wave velocity?
View SolutionThe transverse displacement `y(x, t)` of a wave on a string is given by `y(x, t)= e ^(-(ax^(2) + bt^(2) + 2sqrt((ab))xt)`. This represents a :
View SolutionThe equation of a simple harmonic wave is given by
`y = 3 sin"(pi)/(2) (50t - x)`
where `x` and `y` are in meters and `x` is in second .The ratio of maximum particle velocity to the wave velocity is
View SolutionAt `10^(@)C`, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at `110^(@)C`, this ratio is
View SolutionWhen a string is divided into three segments of length `l_1,l_2` and `l_3` the fundamental frequencies of these three segments are `f_1,f_2` and `f_3` respectively. The original fundamental frequency `f` of the string is
View SolutionA string is stretched between fixed points separated by `75.0cm`. It is observed to have resonant frequencies of `420 Hz` and `315 Hz`. There are no other resonant frequencies between these two. Then, the lowest resonant frequency for this string is
View SolutionThe number of possible natural oscillations of air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are (velocity of sound `=340ms^(-1)`).
View SolutionAn air column, closed at one end and open at the other resonates with a tuning fork when the smallest legnth of the column is 50 cm. The next larger length of the column resonating with the same tuning fork is
View SolutionA uniform rope of legnth `L` and mass `m_1` hangs vertically from a rigid support. A block of mass `m_2` is attached to the free end of the rope. A transverse pulse of wavelength `lamda_1` is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is `lamda_2`. The ratio `(lamda_2)/(lamda_1)` is
View SolutionA uniform string of length `20m` is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is :
(take `g = 10ms^(-2)`)
View SolutionA cylindrical tube open at both ends, has a fundamental frequency `f` in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now
View SolutionThe fundamental frequency of a closed organ pipe of length `20cm` is equal to the equal to the second overtone of an organ pipe open at both the ends. The length of organ pipe open at both the ends is
View SolutionA wave `y = a sin (omegat - kx)` on a string meets with another wave producing a node at `x = 0`. Then the equation of the unknown wave is
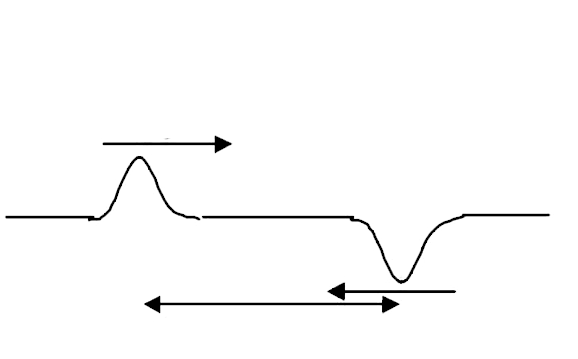
View SolutionTwo pulse in a stretched string whose centers are initially `8cm` apart are moving towards each other as shown in the figure. The speed of each pulse is `2cm//s`. After `2seconds`, the total energy of the pulse will be
View SolutionA travelling wave represented by
`y=Asin (omegat-kx)`
is superimposed on another wave represented by
`y=Asin(omegat+kx).` The resultant is
View SolutionTwo wires are fixed in a sanometer. Their tension are in the ratio `8:1` The lengths are in the ratio `36:35` The diameter are in the ratio `4:1` Densities of the materials are in the ratio `1:2` if the lower frequency in the setting is `360Hz`. The beat frequency when the two wires are sounded together is
View SolutionThe two nearest harmonics of a tube closed at one end and open at other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system?
View SolutionA string of length `0.4 m` and mass `10^(-2)kg` is tightly clamped at its ends. The tension in the string is `1.6 N`. Identical wave pulse are produced at one end at equal intervals of time, `Deltat`. The minimum value of `Deltat` which allows constructive interference of successive pulse is
View Solution
JEE mains adv..(multiple choice quection) questions and complete solutions for chapter OSCILLATIONS AND WAVES of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS OSCILLATIONS AND WAVES
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- conceptual problems
- CURIOSITY QUESTION
- Fill In The Blanks
- Higher Order Thinking Skills
- integer type question
- JEE mains adv..(multiple choice quection)
- Long Answer Questions
- Multiple Choice Question
- Multiple Choice Question-I
- Multiple Choice Question-II
- multiple choice Questions
- NCERT CHAPTER
- NCERT EXERCISES WITH SOLUTIONS
- PROBLEMS FOR PRACTICE
- SAMPLE PROBLEM
- Short Answer Questions
- SOLVED EXAMPLES
- Value Based Questions
- Very Short Answer Questions