Complete Solutions to PART - I of chapter KTG & THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KTG & THERMODYNAMICS |
| RESONANCE | PART - I |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Calorie is defined as the amount of heat required to raise temperature of 1 g of water by `1^@C` and it is defined under which of the following conditions?
View SolutionStatement-1: The total translational kinetic energy of fall the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and its volume because.
Statement-2: The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.
View SolutionAn ideal gas is expanding such that `PT^2=constant.` The coefficient of volume expansion of the gas is-
View Solution`C_v and C_p` denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionThe figure shows the `P-V` plot of an ideal gas taken through a cycle `ABCDA`. The part `ABC` is a semi-circle and `CDA` is half of an ellipseThen
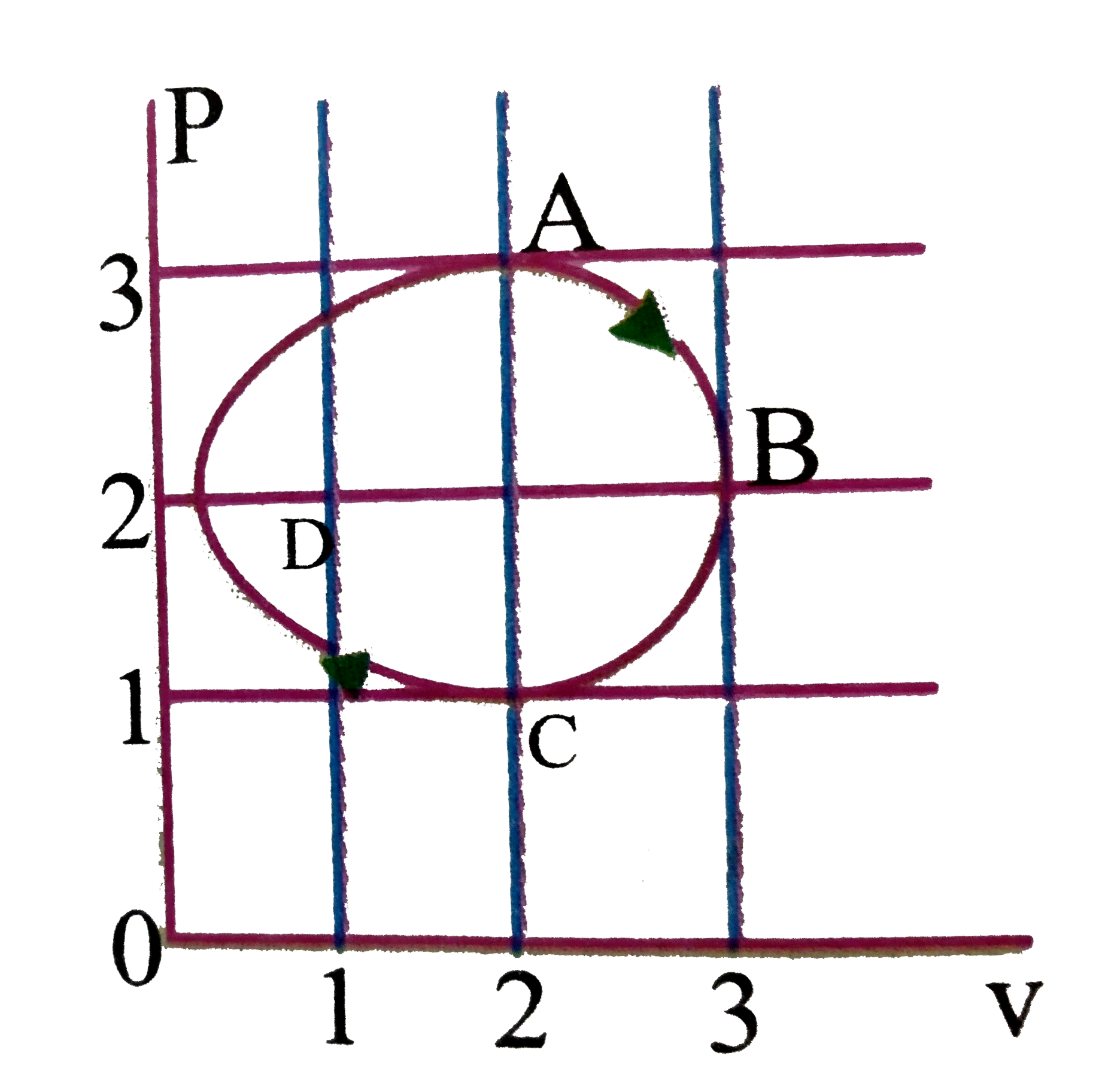
View SolutionA real gas behaves like an ideal gas if its
View SolutionOne mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is `P_0`. Choose the correct option (s) from the following
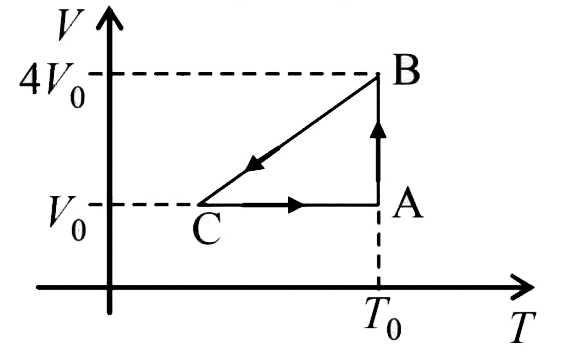
View SolutionA diatomic ideal gas is compressed adiabatically to 1/32 of its initial volume. If the initial temperature of the gas is `T_i` (in Kelvin) and the final temperature is a `T_i`, the value of a is
View Solution5.6 liter of helium gas at STP is adiabatically compressed to 0.7 liter. Taking the initial temperature to be `T_1,` the work done in the process is
View SolutionA mixture of 2 moles of helium gas (` (atomic mass)=4a.m.u` ) and 1 mole of argon gas ( `(atomic mass)=40a.m.u` ) is kept at 300K in a container. The ratio of the rms speeds `((v_(rms)(helium))/((v_(rms)(argon))` is
View SolutionTwo moles of ideal helium gas are in a rubber balloon at `30^@C.` The balloon is fully expandable and can be assumed to require no energy in its expansion. The temperature of the gas in the balloon is slowly changed to `35^@C.` The amount of heat required in raising the temperature is nearly (take R
`=8.31 J//mol.K`)
View SolutionTwo non-reactive monoatomic ideal gases have their atomic masses in the ratio `2:3.` The ratio of their partial pressures, when enclosed in a vessel kept at a constant temperature, is `4:3.` The ratio of their densities is
View SolutionThe figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously form 0 to 500K at a constant rate. Ignoring any volume change, the following statement (s) is (are) correct to a reasonable approximation.
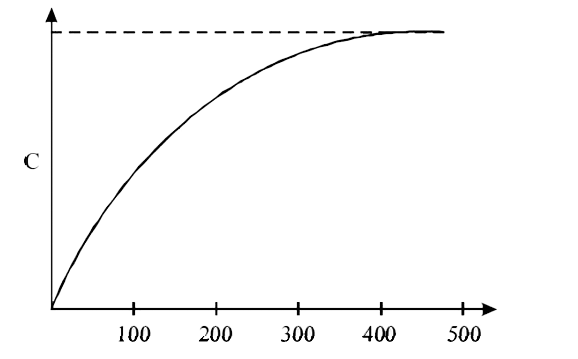
View SolutionA thermodynamic system is taken from an initial state i with internal energy `U_i = 100 J` to the final state f along two different paths iaf and ibf, as schematically shown in the figure. The work done by the system along in the paths af, ib and bf are `W_(af) = 200 J, W _(jb) = 50 J` and `W_(bf) = 100 J` respectively. The heat supplied to the system along the path jaf, jb and are `Q_(jaf), Q_(jb)` and `Q_(bf)` respectively. If the internal energy of the system in the state b is `U_b = 200 J` and `Q_(Ja f)= 500 J`, the ratio `Q_(bf)//Q_(jb) ` is.
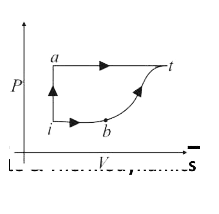
View SolutionIn the figure a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. The heat capacities per mole of an ideal monatomic gas are `C_v = 3/2R, C_p = 5/2 R` and those for an ideal diatomic gas are `C_v = 5/2 R, C_p = 7/2 R`.
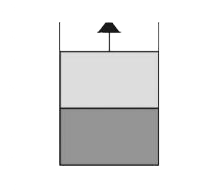
Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be :
View SolutionIn the figure a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. The heat capacities per mole of an ideal monatomic gas are `C_v = 3/2R, C_p = 5/2 R` and those for an ideal diatomic gas are `C_v = 5/2 R, C_p = 7/2 R`.
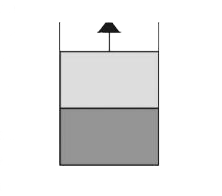
Now consider the partition to be free to move without friction so that the pressure of gasses in both compartments is the same. Then total work done by the gasses till the time they achieve equilibrium done by the gases till the time they achieve equilibrium will be
View SolutionA container of fixed volume has a mixture of a one mole of hydrogen and one mole of helium in equilibrium at temperature T. Assuming the gasses are ideal, the correct statement (s) is (are)
View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature `T_1`, pressure `P_1` and volume `V_1`and the spring is in its relaxed state. The gas is then heated very slowly to temperature `T_2`,pressure `P_2`and volume `V_2`. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View Solution
PART - I questions and complete solutions for chapter KTG & THERMODYNAMICS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS KTG & THERMODYNAMICS
- Advancel Level Problems
- Board Level Exercise
- Examples
- Exercise -1
- Exercise-2
- Exercise-3
- PART - I
- PART - II
- PART -I
- PART -II
- PART -III
- PART -IV
- Problem
- SECTION
- SECTION (A)
- SECTION (B)
- SECTION (C)
- SECTION (D)
- SECTION (E)
- SECTION (F)
- SECTION (G)
- SECTION (H)
- SECTION (I)
- SECTION (J)
- Solved Examples
- Solved problem
- SUBJECTIVE QUESTIONS