Complete Solutions to SECTION of chapter KTG & THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KTG & THERMODYNAMICS |
| RESONANCE | SECTION |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
How is the average KE of a gas molecule related to the temperature of the gas ?
View SolutionWhat is the kinetic interpretation of temperature?
View SolutionState the postulates of kinetic theory of gases?
View SolutionDerive an expression for pressure exterted by an ideal gas?
View SolutionA piece of leads is hammered. Does its internal energy increase? Does the heat enter the lead from outside ?
View SolutionWhat is the change in the internal energy of a system over one complete cycle of a cyclic process?
View SolutionIs the internal energy of a gas a function of the pressure? Explain.
View SolutionRefer to figure. Let `DeltaU_(1)` and `DeltaU_(2)` be the changes in internal energy of the system in the processes A and B. then
View SolutionState and prove law of equipartition of energy.
View SolutionA refrigerator transfers heat from the cold coling coils to the warm surroundings. Is it against the second law of thermodynamics? Justify your answer?
View SolutionAssertion: The temperature of the surface of the sun is approximately `6000 K`. If we take a big lens and focus the sun rays, we can produce a temperature at `8000 K`
Reason: This highest temperature can be produced according to second law of thermodynamics.
View SolutionWhy can a ship not use the internal energy of sea water to operate its engine?
View SolutionA gas has more than one specific heats, whereas a liquid and solid have only one. Why?
OR
Why gas has two principle specific heat capacties.
View Solution(a) Define two specific heats of a gas. Why is `C_(p) gt C_(v)`?
(b) Shown that for an ideal gas,
`C_(p) = C_(v) +(R )/(J)`
View SolutionRepresent equation of an adiabatic process in terms of (i) `T` and `V` (ii) `P` and `T`.
View SolutionIs the equation `PV = RT` valid for both the isothermal and adiabatic changes?
View SolutionDefine and adiabatic process and state two essential conditios for such a process to take place.
View SolutionWhat is meant by reversible engine? Explain, why the efficiency of a reversible engine is maximum.
View SolutionWhat is heat pump ? Name two electric appliances, which work as heat pump.
View SolutionEven carnot heat engine cannot give `100%` efficiency. Explain why
OR
can you design a heat engine of `100%` efficiency? Explain ypur answer.
OR
A heat engine with `100%` efficiency is only a theoretical possibility. Explain.
View SolutionWhat are the conditions for thermodynamic equilibrium?
View SolutionDefine an isothermal process and state two essential conditions for such a process to take place.
View SolutionGive two examples each of (a) an isothermal change and (b) an adiabatic change.
View SolutionWhat are degrees of freedom?
View SolutionWhat is mean free path? Derive an expression for mean free path.
View SolutionAt room temperature `(300K)`, the rms speed of the molecules of a certain diatomic gas is found to be `1930 m//s`. Can you gusess name of the gas? Find the temperature at which the rms speed is double of the speed in part one `(R = 25//3 J// mol -K)`
View SolutionThe average translational kinetic energy of nitrogen gas molecule is `0.02eV (1eV - 1.6 xx 10^(-19)J)`. Calculate the temperatuire of the gas. Boltzmann constant `k = 1.38 xx 10^(-23) J//K`.
View SolutionA gas is filled in a container at pressure `P_(0)`. If the mass of molecules is halved and their rms speed is doubled, then the resultant pressure would be
View SolutionThe molecule of a given mas of gas have r.m.s. speed `200 ms^(-1)` at `27^(@)C` and `10^(5)Nm^(-2)` pressure. When the absolute temperature is doubled and the pressure is halved, then find rms speed of the molecules of the same gas.
View SolutionButane gas burns in air according to the following reaction.
`2C_(4)H_(10) +13O_(2) rarr 10 H_(2)O +8 CO_(2)`.
Suppose the initial and final temperature are equal and high enough so that all reactants and products act as perfect gases. Two moles of butane ar mixed with `13` moles of oxygen and then completely reacted. Find the final pressure (if the volume remains unchanged and the pressure before reaction is `P_(0))`?
View SolutionA cylinder contains gas at `2 xx 10^(5) Pa`and `47^(@)C`. The cylinder is steadily heated. Neglecting any change in its volume, find the temperature at which the cylinder will break if the walls of cylinder can bear a maximum pressure of `8 xx 10^(5) Pa`
View SolutionAt a pressure of `3` atm air (treated as an ideal gas) is pumped into the tubes of a cycle rickshaw. The volume of each tube at given pressure is `0.004 m^(3)`. One of the tubes gets punctured and the volume of the tube reduces to `0.0008 m^(3)`. Find the number of moles of air that have leaked out? Assume that the temperature remains constant at `300K. (R = 25//3J mol^(-1)K^(-1))`
View SolutionA vessel contains `0.5g` of hydrogen and `0.8g` of oxygen. The volume of vessel is `(5)/(28)m^(3)` while its temperature is maintanied at `300K`. Find the pressure of the mixture. (Assuming no reaction takes place between hydrogen and oxygen) `(M_(H_(2)) =2 , M_(O_(2)) = 32 & R = (25)/(3) J//mol-K)`
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury `5cm` long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is `30cm`. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure `=75cm` of mercury. (Assume temperature remains constant in this process)

View Solution(i) A conducting cylinder whose inside diameter is `4.00cm` contains air compressed by a piston of mass `m = 13.0 kg`, which can slides freely in the cylinder shown in the figure. The entire arrangement is immersed in a water bath whose temperature can be controlled. The syetem is initially in equilibrium at temperature `t_(1) = 20^(@)C`. The initial height of the piston above the bottom of the cylinder is `h_(i) = 4.00 cm. P_(atm) =1 xx 10^(5) N/m^(2)` and `g = 10m//s^(2)`.
If the temperature of the water bath is gradually increased to a final temperature `t_(f) = 100^(@)C`. Find teh height `h_(f)` of the piston (in cm) at that instant?
(ii) In the above question, if we again start from the initial conditions and the temperature is again gradually raised, and weights are added to the piston to keep its height fixed at `h_(i)`. Find the value of teh added mass when the final temperature becomes `t_(f) = 100^(@)C`?

View SolutionFind the average of magnitude of linear momentum of helium molecules in a sample of helium gas at temperature of `150 piK`. Mass of a helium molecules `=(166//3) xx 10^(-27) kg` and `R = 25//3J-mol^(-1)K^(-1)`
View SolutionThe mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
View SolutionThe following graphs shows two isotherms for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at tempertaures `T_(1)` and `T_(2)`?
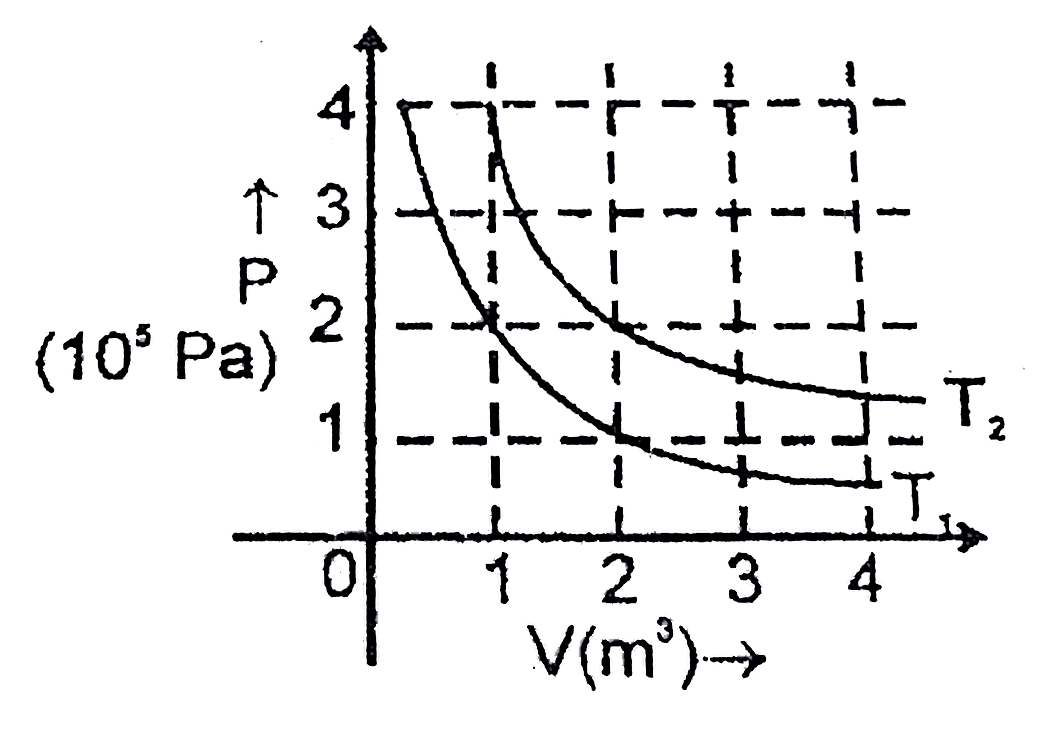
View Solution`0.040g` of He is kept in a closed container initially at `100.0^(@)C.`The container is now heated. Neglecting the expansion of the container, Calculate the temperature at which the internal energy is increased by `12J`.
View SolutionShow that the internal energy of the air (treated as an ideal gas) contained in a room remains constant as the temperature changes between day and night. Assume that the atmospheric pressure around remains constant and the air in the room maintains this pressure by communicating with the surrounding through the windows, doors, etc.
View SolutionAn insulated box containing a monoatomic gas of molar mass (M) moving with a speed `v_0` is suddenly stopped. Find the increment is gas temperature as a result of stopping the box.
View SolutionFind the work done by gas going through a cyclic process shown in figure?
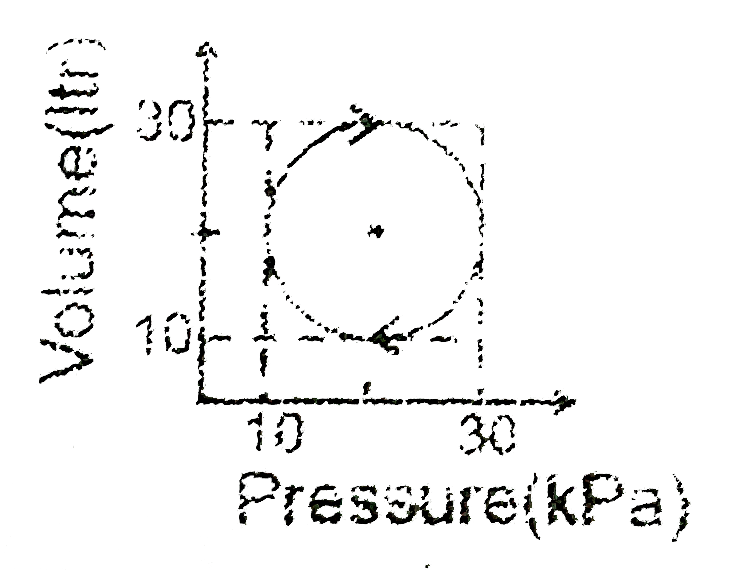
View SolutionAn ideal gas is compressed at constant pressure of `10^(5)Pa` until its volume is halved. If the initial volume of the gas as `3.0 xx 10^(-2)m^(3)`, find the work done on the gas?
View SolutionDetermine the work done by an ideal gas doing `1 rarr 4 rarr 3rarr 2 rarr 1`.
Given `P_(1) = 10^(5) Pa, P_(0) = 3 xx 10^(5) Pa, P_(3) = 4 xx 10^(5) Pa` and `V_(2) - V_(1) = 10 L`.

View SolutionFind the expression for the work done by a system undergoing isothermal compression (or expansion) from volume `V_(1)` to `V_(2)` at temperature `T_(0)` for a gas which obeys the van der waals equation of state. `(P +an^(2) //V^(2)) (V-bn) =nRT`?
View SolutionA system absorbs `1000` cal of heat and does `1675J` work. If `J = 4.18 J//cal`, then find the change in internal energy of the system?
View SolutionA cylinder fitted with a piston contains an ideal monoatomic gas at a temperature of `400K`. The piston is held fixed while heat `DeltaQ` is given to the gas, it is found the temperature of the gas has increased by `20K`. In an isobaric process the same `DeltaQ` heat is supplied slowely to it. Find the change in temperature in the second process?
View SolutionIn a thermodynamic process, pressure of a fixed mass of a gas is changed in such a manner that the gas release `20 J` of heat and `8 J` of work is done on the gas. If initial internal energy of the gas was `30 J`, what will be the final internal energy?
View SolutionA diatomic gas done `80J` work when expanded isobarically. Find the heat given to the gas during this process?
View SolutionWhen `1g` of water at `0^(@)C` and `1 xx 10^(4)Nm^(-2)` pressure is converted into ice of volume `1.091 cm^(3)`, find the work done by water? `(rho_(w) = 1 gm//cm^(3))`
View SolutionAn ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are `Q_1=5960J, Q_2=-5585J, Q_3=-2980J and Q_4=3645J`, respectively. The corresponding quantities of work involved are `W_1=2200J, W_2=-825J, W_3=-1100J and W_4` respectively.
(1) Find the value of `W_4`.
(2) What is the efficiency of the cycle
View SolutionIn given figure, gas is slowely heated for sometime. During the process, the increases in internal energy of the gas is `10J` and the piston is found to move out by `25cm`, then find the amount of heat supplied. The area of cross-section of cylinder `= 40cm^(2)` and atmospheric pressure `100 kPa`
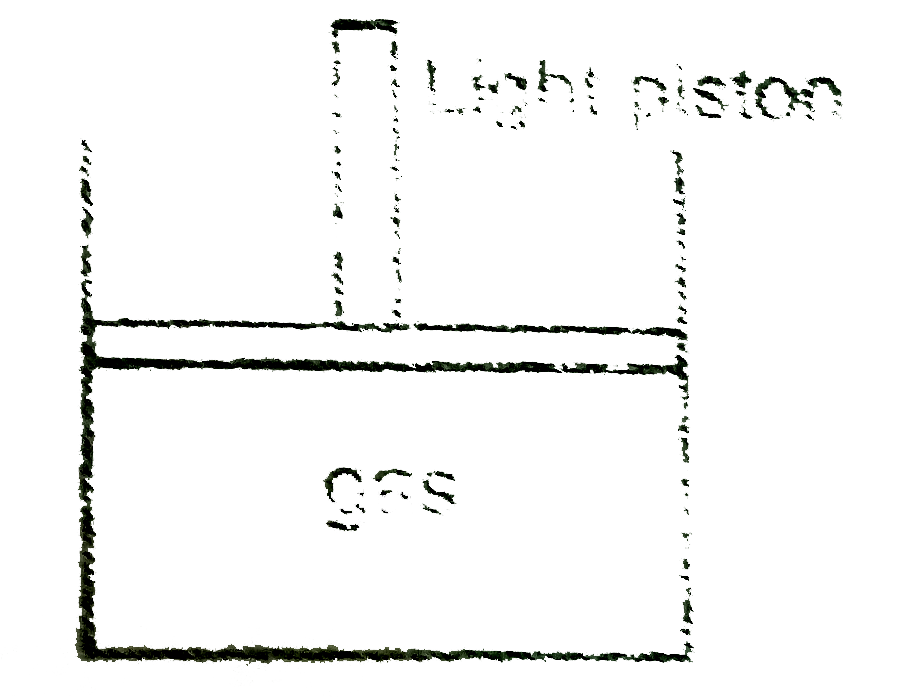
View SolutionA gas is initially at a pressure of `100 kPa` and its volume is `2.0 m^(3)`. Its pressure is kept constant and the volume is changed from `2.0 m^(3)` to `2.5 m^(3)`. Its volume is now kept constant and the pressure is increased from `100 kPa` to `200 kPa`. The gas is brought back to its initial state, the pressure varying linearly with its volume.
(a) Whether the heat is supplied to or exerted from the gas in the complete cycle ?
(b) How much heat was supplied or extracted ?
View SolutionFind the change in the internal energy of `2 kg` of water as it heated from `0^(0)C to 4^(0)C`. The specific heat capacity of water is `4200 J kg^(-1) K^(-1)` and its densities at `0^(0)C` and `4^(0)C` are `999.9 kg m^(-3)` and `1000 kg m^(-3)` respectively. atmospheric pressure `=10^(5)` Pa.
View SolutionIn given figure, An ideal gas a gas is taken through a cyclic process `ABCA`, calculate the value of meachanical equilvalent of heat `(J)` when `4.8cal` of heat is given in the process?
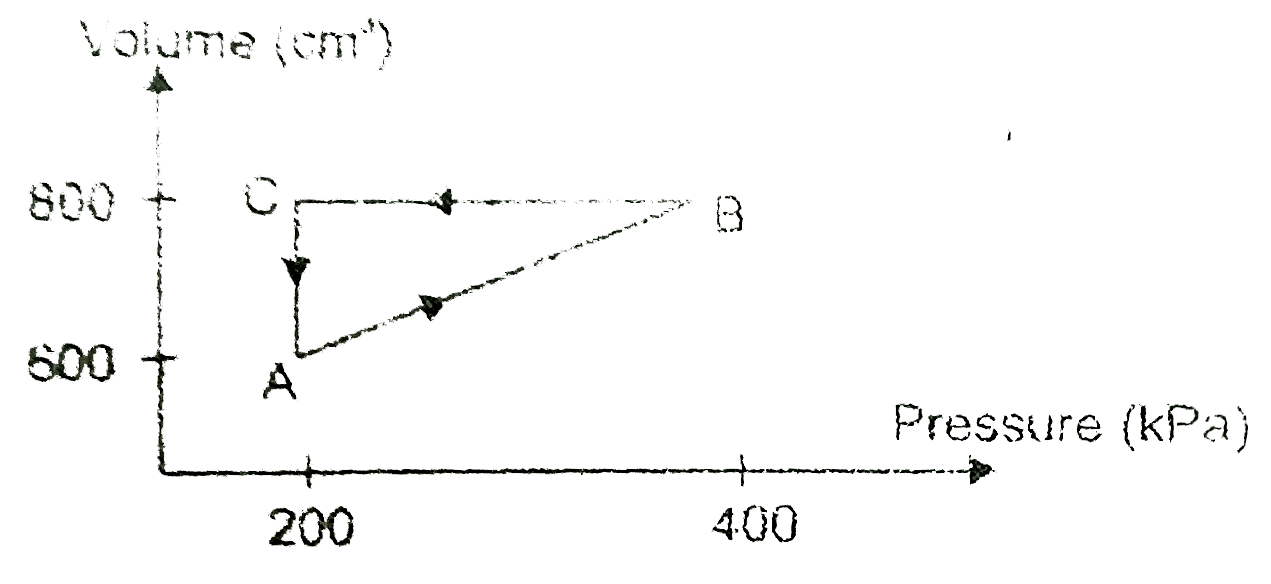
View SolutionAn ideal gas is taken through the process `ABC` as shown in figure. If the internal energy of the substance decreases by `10000J` and a heat of `7159` cal is released by the system, calculate the value of meachanical equivalent of heat `(J)`.
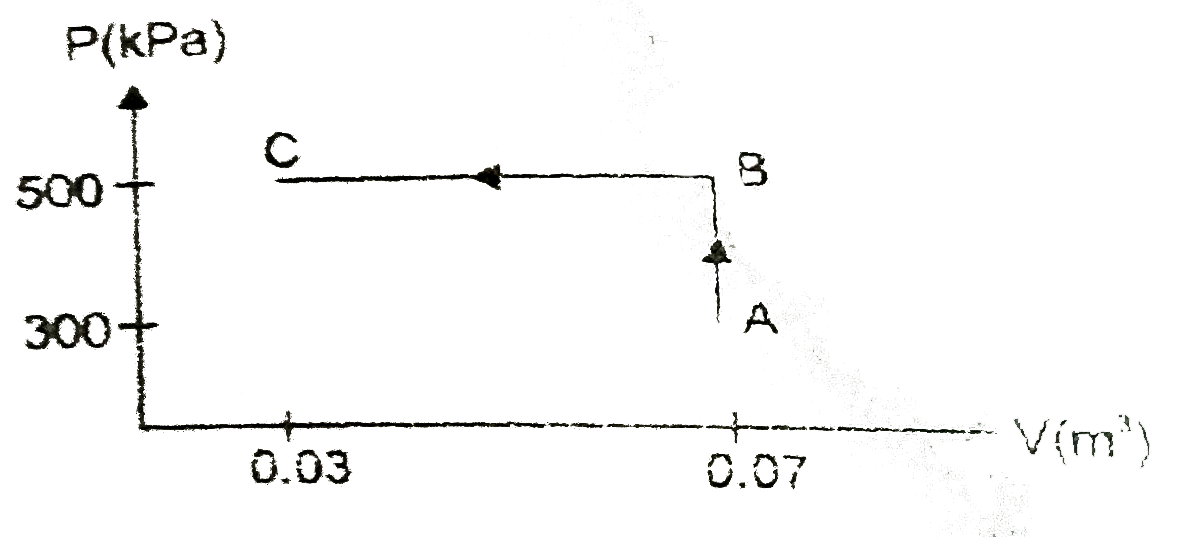
View SolutionIn given figure, one mole of an ideal gas `(gamma = 7//5)` is taken through the cyclic process `ABCDA`.
Take `R = (25)/(3) J//mol -K`
(a) Find the temperature of the gas in states `A,B,C` and `D`.
(b) Find the amount of heat supplied/released in processes `AB,BC,CD` and `DA`.
(c) Find work done by gas during cyclic process.

View Solution70 calories of heat required to raise the temperature of 2 moles of an ideal gas at constant pressure from `30^@Cto 35^@C.` The amount of heat required (in calories) to raise the temperature of the same gas through the same range `(30^@C to 35^@C)` at constant volume is:
View SolutionInternal energy of two moles of an ideal gas at a temperature of `127^(@)C is 1200R`. Then find the molar specific heat of the gas at constant pressure?
View SolutionIdeal monoatomic gas is taken through a process `dQ = 2dU`. Find the molar heat capacity (in terms of `R)` for the process? (where `dQ` is heat supplied and `dU` is change in internla energy)
View SolutionCalculate the value of mechanical equivalent of heat from the following data. Specific heat capacity of air at constant volume and at constant pressure are `4.93 cal//mol-K` and `6.90 cal//mol-K` respectively. Gas constant `R = 8.3 J//mol-K`.
View SolutionFind the change in internal energy of `2` moles of an ideal gas when its temperature is increased by `75K`
(a) Keeping the pressure constant.
(b) Keeping the volume constant and
(c ) adiabatically. `(gamma = (C_(P))/(C_(V)) =(7)/(5)) [R = (25)/(3)J//mol-K]`
View SolutionWhen `100J` of heat is given to an ideal gas it expands from `200cm^(3)` to `400cm^(3)` at a constant pressure of `3 xx 10^(5) Pa`. Calculate (a) the change in internal energy of the gas (b) the number of moles in the gas if the initial temperature is `400K`, (c ) the molar heat capacity `C_(p)` at constant pressure and (d) the molar heat capacity `C_(v)` at constant volume. `[R = (25)/(3)J//mol-K]`
View SolutionThe temperature of `5 mol` of gas which was held at constant volume was change from `100^(@)C` to `120^(@)C`. The change in internal energy was found to ve `80 J`. The total heat capacity of the gas at constant volume will be equal to
View SolutionFor a gas `gamma = 9//7`. What is the number of degrees of freedom of the molecules of this gas ?
View SolutionIf one mole of a monatomic gas `(gamma=5/3)` is mixed with one mole of a diatomic gas `(gamma=7/5),` the value of gamma for mixture is
View SolutionThe pressure and density of a diatomic gas `(gamma=7//5)` change adiabatically from (p,d) to `(p^('),d^('))`. If `(d^('))/(d)=32`, then `(P^('))/(P)` should be
View SolutionAn ideal gas `(gamma = (5)/(3))` is adiabatically compressed from `640 cm^(3)` to `80cm^(3)`. If the initial pressure is `P` then find the final pressure?
View SolutionIn a adiabatic process pressure is increased by `2//3%` if `C_(P)//C_(V) = 3//2`. Then the volume decreases by about
View SolutionAn ideal gas at pressure `4 xx 10^(5)Pa` and temperature `400K` occupies `100cc`. It is adiabatically expanded to double of its original volume. Calculate (a) the final pressure (b) final temperature and (c ) work done by the gas in the process `(gamma = 1.5)`
View SolutionIn fig. the walls of the container and the piston are weakly conducting. The initial pressure, volume and temperature of the gas are `200KPa, 800 cm^(3)` and `100 K resp`. Find the pressure and the temperature of the gas it it is (a) slowly compressed (b) suddenly compressed to `200 cm^(3) (gamma = 1.5)`.

View SolutionWhen the state of a system changes from `A` to `B` adiabatically the work done on the system is `322` joule. If the state of the same system is changed from `A` to `B` by another process, and heat required is `50` calories of heat is required then find work done on the system in this process? `(J = 4.2 J//cal)`
View SolutionIf `Q` amount of heat is given to a diatomic ideal gas in a process in which the gas perform a work `(2Q)/(3)` on its surrounding. Find the molar heat capacity (in terms of `R`) for the process.
View SolutionAn ideal gas is taken through a process in which pressure and volume vary as `P = kV^(2)`. Show that the molar heat capacity of the gas for the process is given by `C = C_(v) +(R )/(3)`.
View SolutionAn ideal gas `(C_p / C_v = gamma)` is taken through a process in which the pressure and volume vary as `(p = aV^(b))`. Find the value of b for which the specific heat capacity in the process is zero.
View SolutionWhat is the principle of least time?
View SolutionThe efficiency of Carnot's enegine is `50%`. The temperature of its sink is `7^(@)C`. To increase its efficiency to `70%`. What is the increase in temperature of the source?
View SolutionA Carnot engine work as refrigerator in between `0^(@)C` and `27^(@)C`. How much energy is needed to freeze `10 kg` ice at `0^(@)C`/
View SolutionWhat is the change in velocity in the above question?
View SolutionA Carnot engine works as a refrigerator in between `250K` and `300K`. If it acquires `750` calories form heat source at low temperature, then what is the heat generated at higher temperature (in calories)?
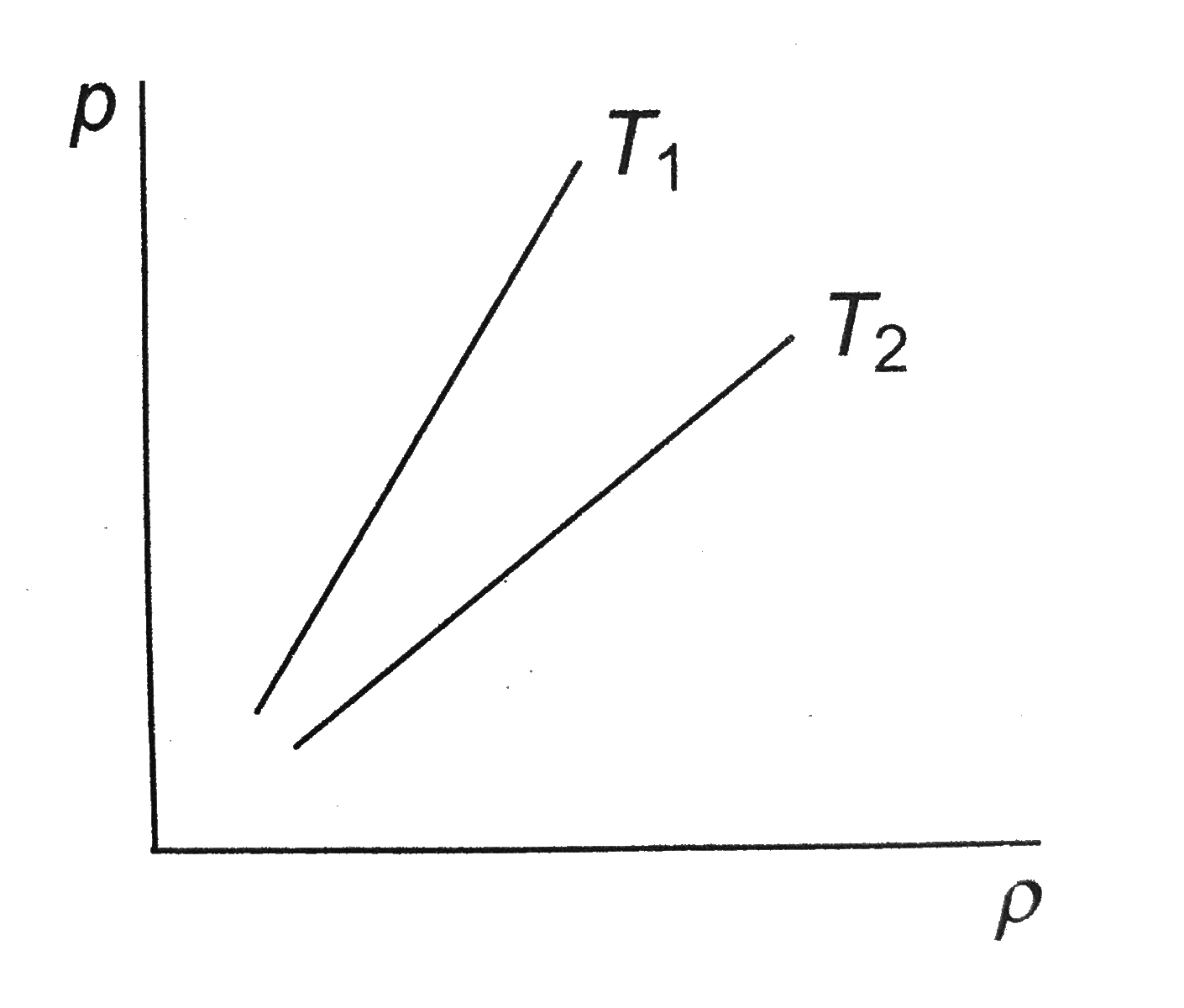
View SolutionFigure shows graphs of pressure vs density for an ideal gas at two temperature `T_(1) and T_(2)`. Which of the following is correct?
View SolutionSuppose a container is evacuated to leave just one molecule of a gas in it. Let `v_(mp)` and `v_(av)` represent the most probable speed and the average speed of the gas, then
View SolutionThe average speed of nitrogen molecules in a gas is `v`. If the temperature is doubled and the `N_(2)` molecule dissociate into nitrogen atoms, then the average speed will be
View SolutionKeeping the number of moles, volume and pressure the same, which of the following are the same for all ideal gas?
View SolutionFour containers are filled with monoatomic ideal gases. For each container , the number of moles , the mass of an individual atom and the rms speed of the atoms are expressed in terms of n , m and `v_("rms")` respectively . If `T_(A) , T_(B) , T_(C)` and `T_(D)` are their temperatures respectively then which one of the options correctly represents the order ?
_E01_052_Q01.png)
View SolutionFor a gas sample with `N_(0)` number of molecules, function `N(V)` is given by: `N(V) = (dN)/(dV) = ((3N_(0))/(V_(0)^(3)))V^(2)` for `0 lt V lt V_(0)` and `N(V) = 0` for `V gt V_(0)`. Where `dN` is number of molecules in speed range `V` to `V+ dV`. The rms speed of the molecules is:
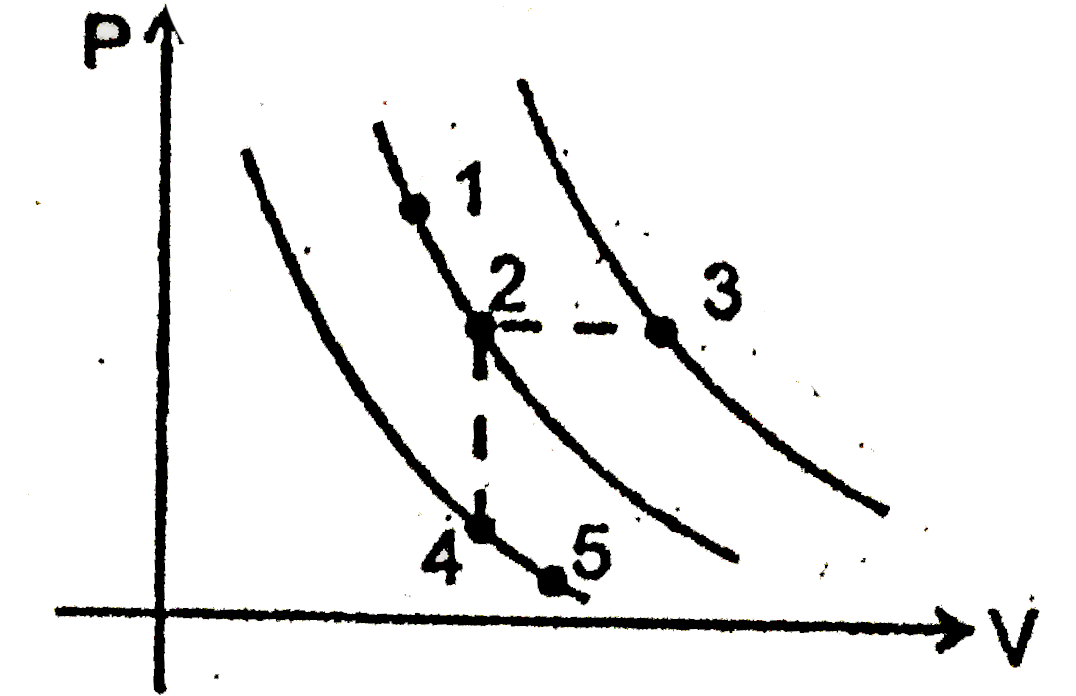
View SolutionA certain gas is taken to the five states representes by dots in the graph. The plotted lines are isotherms. Order of the most probable speed `v_(p)` of the molecules at these five states is
View SolutionWhich of the following quantities is the same for all ideal gases at the same temperature?
View SolutionRefer to figure. Let `DeltaU_(1)` and `DeltaU_(2)` be the changes in internal energy of the system in the processes A and B. then
View SolutionThe quantity `(2U)/(fkT)` represents (where `U =` internal energy of gas)
View SolutionAn ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?

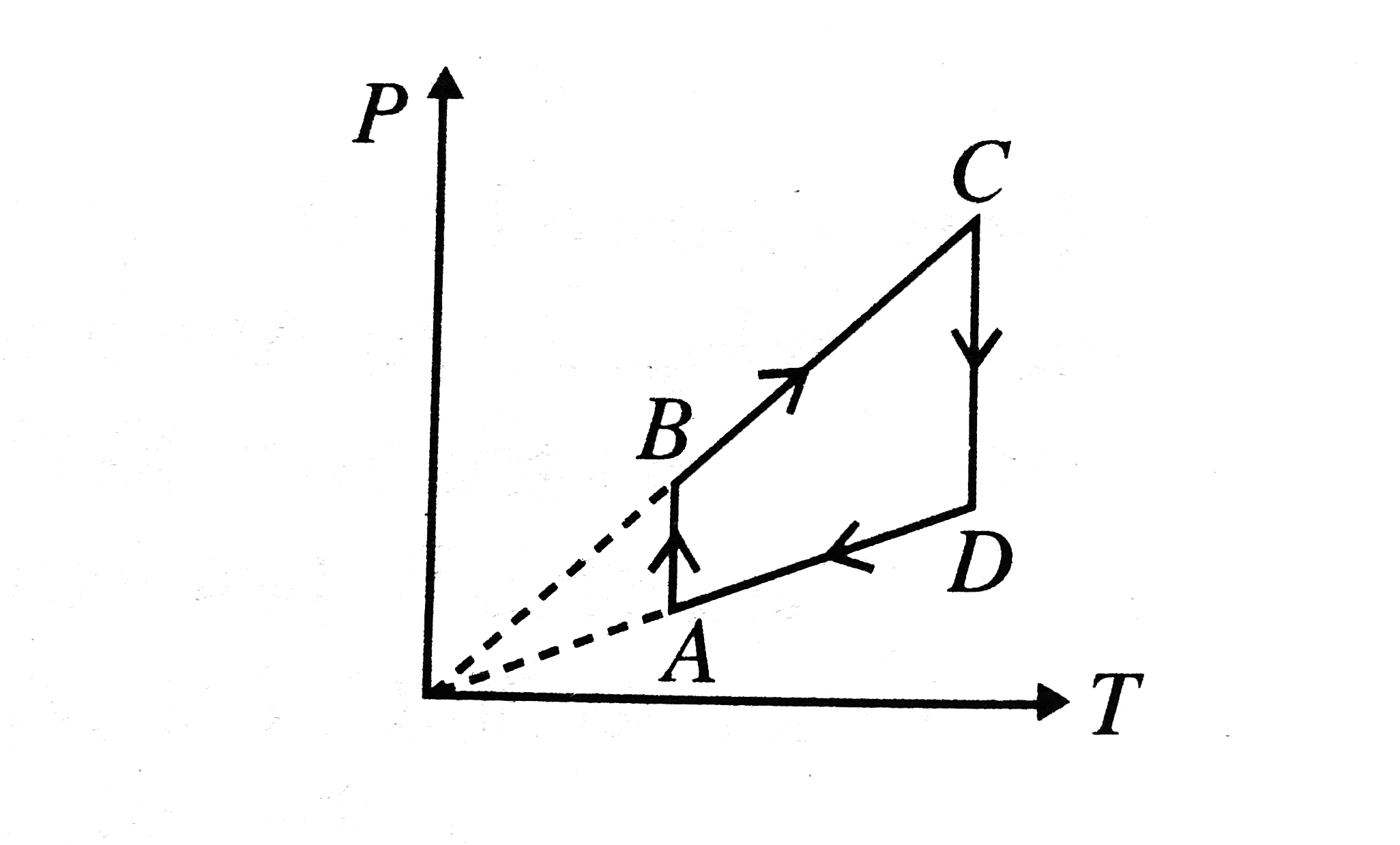
View SolutionPressure versus temperature graph of an ideal gas as shown in Fig.
Corresponding density `(rho)` versus volume `(V)` graph will be
View SolutionThe process `DeltaU = 0`, for an ideal gas can be best represented in the form of a graph:
View SolutionIn the given (V-T) diagram, what is the relation between pressure `P_(1) and P_(2)` ?

View SolutionIn a cyclic process shown on the `P -V` diargam the magnitude of the work done is :

View SolutionA fixed mass of an ideal gas undergoes changes of pressure and volume starting at `L`, as shown in Figure. Which of the the following is correct:

View SolutionIn figure, `P-V` curve of an ideal gas is given. During the process, the cumulative work done by the gas
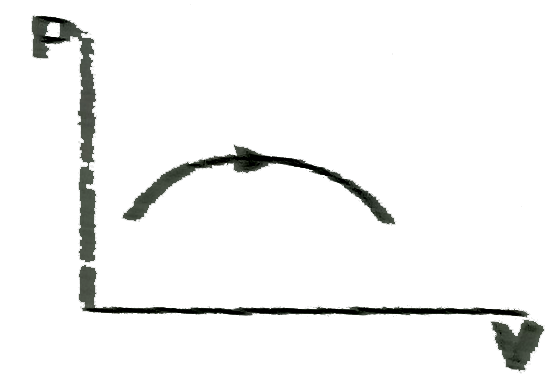
View SolutionConsider two processes on a system as shown in figure.
The volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let `DeltaW_(1)` and `DeltaW_(2)` be the work done by the system in the processes `A` and `B` respectively.

View SolutionA mass of an ideal gas undergoes a reversible isothermal compression. Its molecules will then have compared with initial state, the same
(i) rrot mean square velocity (ii) mean mometum (iii) mean kinetic energy
View SolutionIn the above question, if the work done on the system along the curved path 'ba' is `52J`, heta abosrbed is
View Solution
SECTION questions and complete solutions for chapter KTG & THERMODYNAMICS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS KTG & THERMODYNAMICS
- Advancel Level Problems
- Board Level Exercise
- Examples
- Exercise -1
- Exercise-2
- Exercise-3
- PART - I
- PART - II
- PART -I
- PART -II
- PART -III
- PART -IV
- Problem
- SECTION
- SECTION (A)
- SECTION (B)
- SECTION (C)
- SECTION (D)
- SECTION (E)
- SECTION (F)
- SECTION (G)
- SECTION (H)
- SECTION (I)
- SECTION (J)
- Solved Examples
- Solved problem
- SUBJECTIVE QUESTIONS