Complete Solutions to PART -I of chapter KTG & THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KTG & THERMODYNAMICS |
| RESONANCE | PART -I |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
The given curve represents the variation of temperatue as a function of volume for one mole of an ideal gas. Which of the following curves best represents the variation of pressure as a function of volume ?
 .
.
View SolutionConsider a hypotheticla gas with molecules that can move along only a single axis. The following table givesfour situations. The velocities is meter per seocond of such a gas having four molecules. The plus and minus sign refer to the direction of the velcoity along the axis.
`{:(ul("Situation Velocities"),,,,),("a -2 +3 -4 +5",,,,),(-------------,,,,),("b +1 -3 +4 -6",,,,),(-------------,,,,),("c +2 +3 +4 +5",,,,),(-------------,,,,),("d +3 +3 -4 -5",,,,),(-------------,,,,):}`
In which situation root-square speed of the molecules is greatest
View SolutionThe value of `C_(p) - C_(v)` is `1.09R` for a gas sample in state `A` and is `1.00R` in state `B`. Let `A_(A),T_(B)` denote the temperature and `p_(A)` and `P_(B)` denote the pressure of the states `A` and `B` respectively. Then
View SolutionFind work done by the gas in the process shown in figure.

View SolutionAn ideal monoatomic gas undergoes the process AB as shown in the figure. If the heat supplied and the work done in the process are `DeltaQ` and Delta W` respectively. The ratio `DeltaQ : DeltaW` is
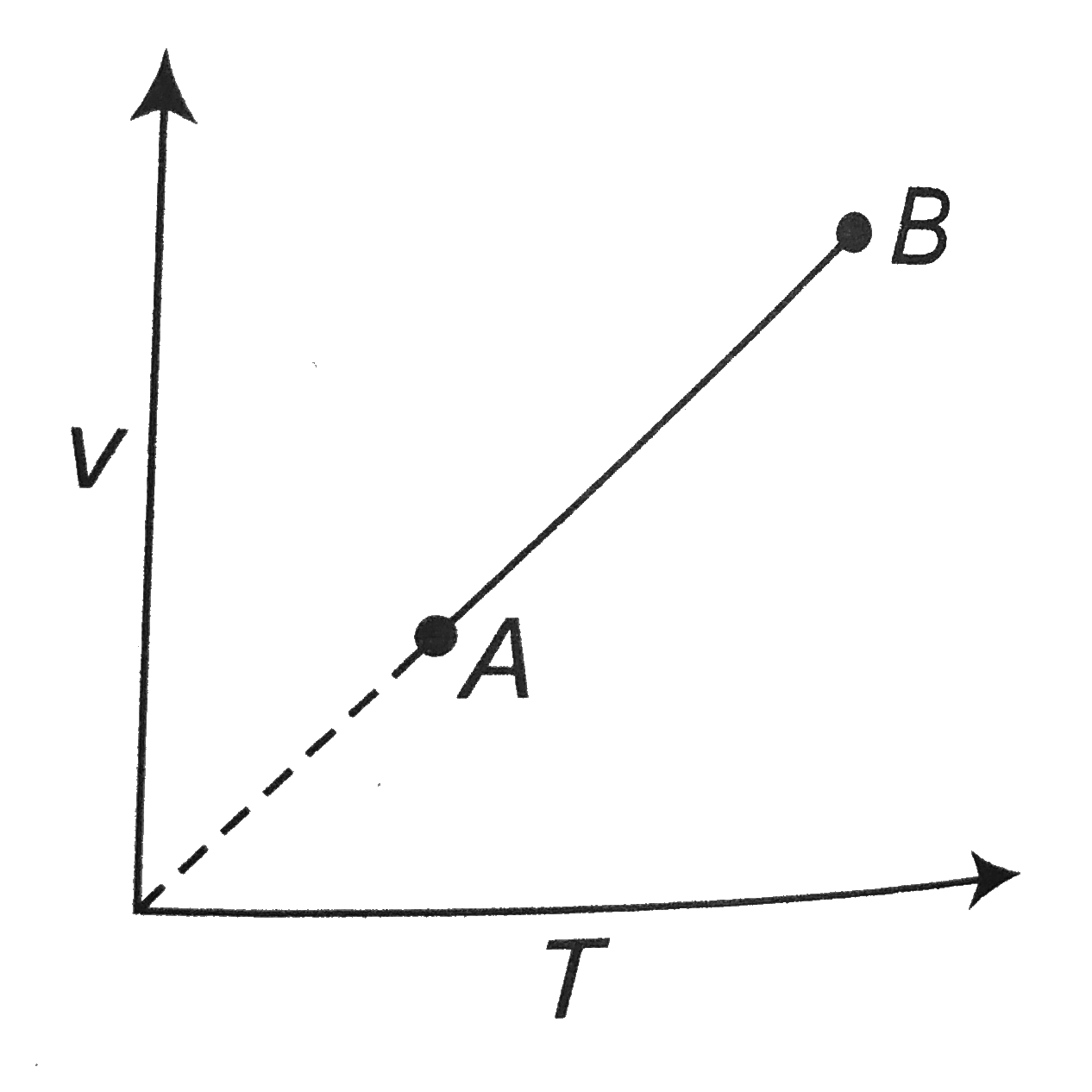
View SolutionAn ideal monoatomic gas is initially in state `1` with pressure `p_(1) = 20 atm` and volume `v_(1) = 1500 cm^(3)`. If is then taken to state `2` with pressure `p_(2) = 1.5 p_(1)` and volume `v_(2) = 2v_(1)`. The change in internal energy from state `1` to state `2` is equal to
View SolutionFor two thermodynamic process temperature and volume diagram are given. In first process, it is a straight line having initial and final coordinates as `(V_(0),T_(0))` and `(2V_(0), 2T_(0))`, where as in second process it is a rectangular hyperbola having intial and final coordinates `(V_(0),T_(0))` and `(2V_(0), T_(0)//2)`. Then ratio of work doen in the two process must be
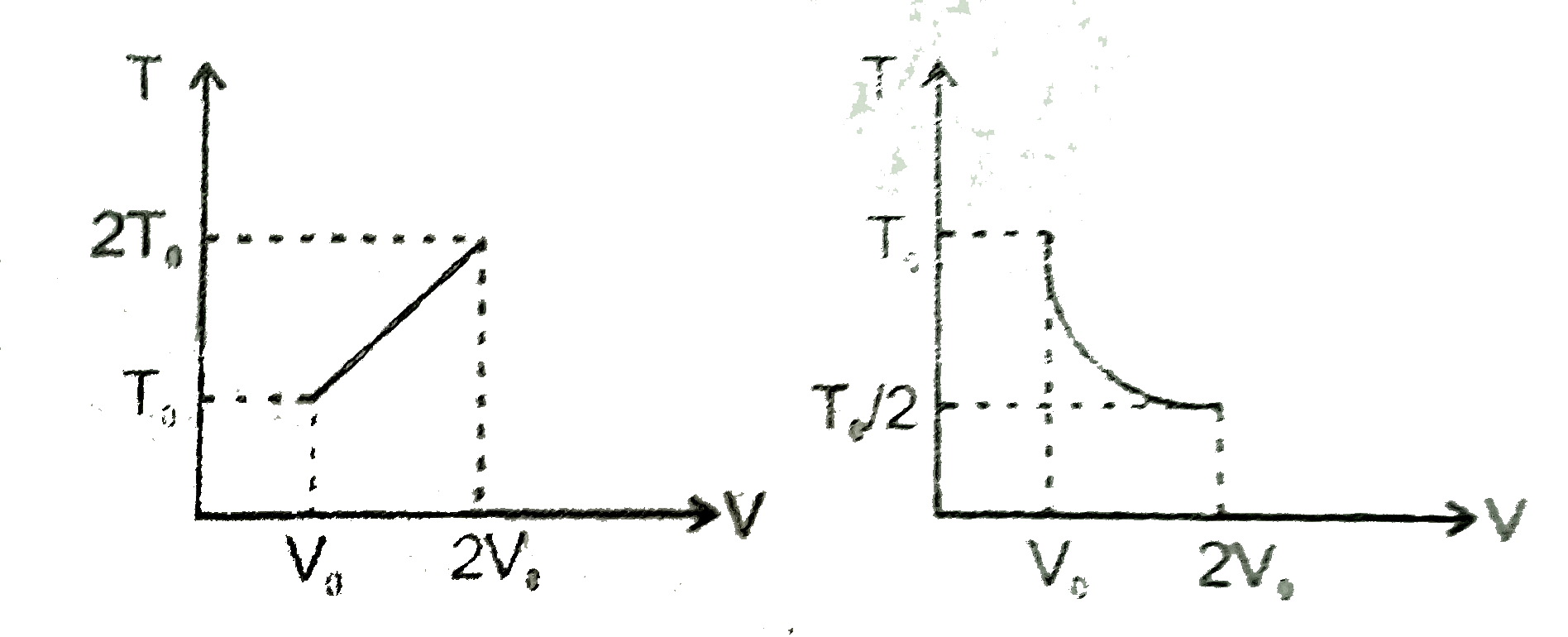
View SolutionCurve in the figure shows an adiabatic compression of an ideal gas from `15m^3` to `12m^3`, followed by an isothermal compression to a final volume of `3.0m^3`. There are 2.0 moles of the gas. Total heat supplied to the gas is equal to: (ln2= 0.693)
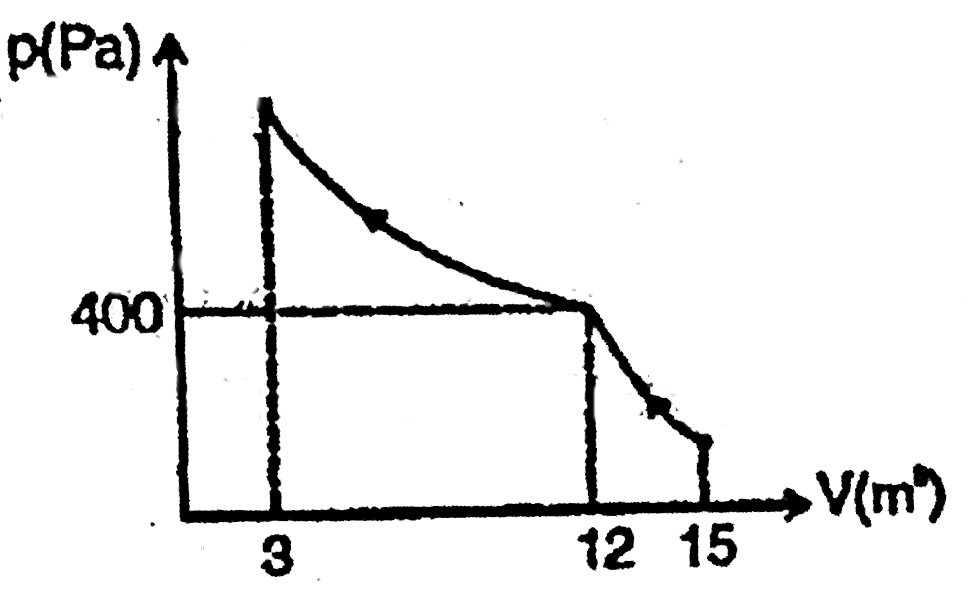
View Solution`P_(i), V_(i)`are initial pressure and volumes and `V_(f)` is final volume of a gas in a thermodynamic process respectively. If `PV^(n) =` constant, then the amount of work done by gas is`: (gamma = C_(p)//C_(v))`. Assume same, initial states & same final volume in all processes.
View SolutionA cylinder containing an ideal gas ( see figure ) and closed by a movable pistong is submerged in an ice- water mixture. The pistone is quickly pushed down from position (1) to position (2)( process `AB)`. The piston is held at position `(2)` until the gas is again at `0^(@)C` ( processs `BC)`. Then the pistone is slowly raised back to position (1) ( process `CA)`
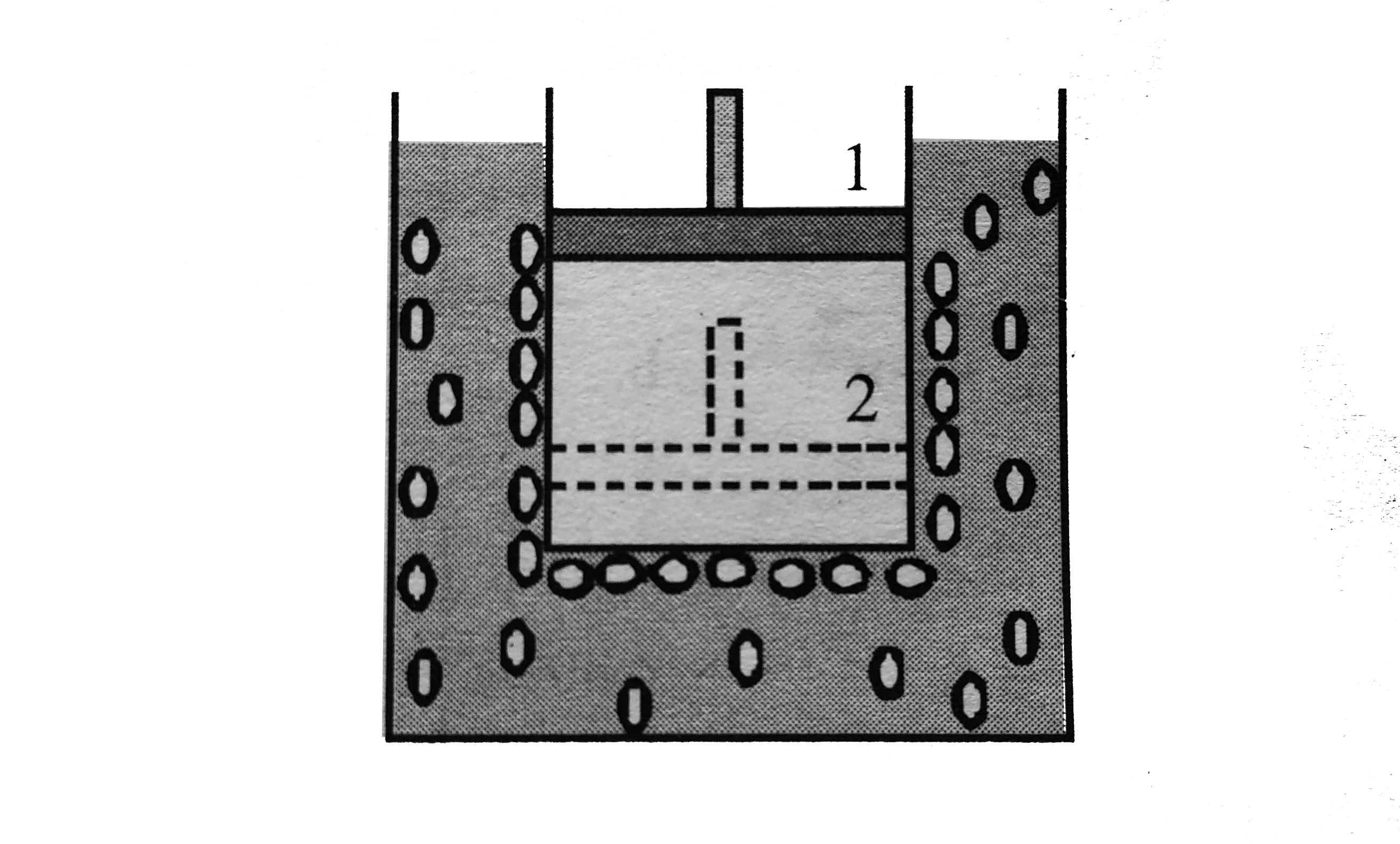
Which of the following `P-V` diagram will correctly represent the processes `AB, BC` and `CA` and the cycle `ABCA?`
View SolutionTwo different ideal diatomic gases `A` and `B` are initially in the same state. `A` and `B` are then expanded to same final volume through adiabatic and isothermal process respectively. If `P_(A), P_(B)` and `T_(A), T_(B)` represents the final pressure and temperature of `A` and `B` respectively then.
View SolutionIf ideal diatomic gas follows the process, as shown in graph, where `T` is temperature in kelvin and `V` is volume `(m^(3))`, then molar heat capacity for this process will be [in terms of gas constant `R]`:

View SolutionA mono-atomic ideal gas is compressed form volume `V` to `V//2` through various process. For which of the following processes final pressure will be maximum:
View Solution`4` moles of `H_(2) at 500K` is mixed with `2` moles of `He` at `400k`. The mixture attains a temperature `T` and volume `V`. Now the mixture is compressed adiabatically to a volume `V'` and temperature `T'`. If `(T')/(T) = ((V)/(V'))^(n)`, find the value of `13n`.
View SolutionIn a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
View Solution
PART -I questions and complete solutions for chapter KTG & THERMODYNAMICS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS KTG & THERMODYNAMICS
- Advancel Level Problems
- Board Level Exercise
- Examples
- Exercise -1
- Exercise-2
- Exercise-3
- PART - I
- PART - II
- PART -I
- PART -II
- PART -III
- PART -IV
- Problem
- SECTION
- SECTION (A)
- SECTION (B)
- SECTION (C)
- SECTION (D)
- SECTION (E)
- SECTION (F)
- SECTION (G)
- SECTION (H)
- SECTION (I)
- SECTION (J)
- Solved Examples
- Solved problem
- SUBJECTIVE QUESTIONS