Complete Solutions to SUBJECTIVE QUESTIONS of chapter KTG & THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KTG & THERMODYNAMICS |
| RESONANCE | SUBJECTIVE QUESTIONS |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A vessel of volume `V` is evacuated by means of a piston air pump. One piston stroke captures the volume `Delta V`. How many strokes are needed to reduce the pressure in the vessel `eta` times ? The process is assumed to be isothermal, and the gas ideal.
View SolutionFind the pressure of air in a vessel being evacuated as a function of evacuation time `t`. The vessel volume is `V`, the initial pressure is `p_0`. The process is assumed to be isothermal, and the evacuation rate equal to `C` and independent of pressure.
The evatuation rate is the gas volume being evacuated per unit time, with that volume being measured under the gas pressure attained by that moment.
View SolutionFind the maximum attainable temperature of ideal gas in each of the following process :
(a) `p = p_0 - alpha V^2` ,
(b) `p = p_0 e^(- beta v)`,
where `p_0, alpha` and `beta` are positive constants, and `V` is the volume of one mole of gas.
View SolutionTwo moles of an ideal monoatomic gas are contained in a vertical cylinder of cross sectional area `A` as shown in the figure. The piston is frictionless and has a mass m. At a certain instant a heater starts supplying heat to the gas at a constant rate `q J//s`. Find the steady velocity of the piston under isobaric condition. All the boundaries are thermally insulated.

View SolutionA piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volume `V_0` in which an ideal gas is contained under the same pressure `p_0` and at the same temperature. What work has to be performed in order to increase isothermally the volume of one part of gas `eta` times compared to that of the other by slowly moving the piston ?
View SolutionAt `27^@C` two moles of an ideal monoatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas, (ii) change in its internal energy, and (iii) the work done by the gas during this process.
View SolutionA vertical hollow cylinder contains an ideal gas. The gas is enclosed by a `5kg` movable piston with an area of cross-section `5 xx 10^(-3)m^(2)`. Now, the gas is heated slowly from `300K` to `350K` and the piston rises by `0.1m`. The piston is now clamped at this position and the gas is cooled back to `300K`. Fid the difference between the heat energy added during heating process and energy lost during the cooling process. `("1atm pressire" = 10^(5)Nm^(-2)]`
View SolutionA sample of 2 kg of monatomic helium (assumed ideal) is taken through the process ABC another sample of 2 kg of the same gas is taken through the process ADC as shown in Fig. Given molecular mass of helium = 4.
a. What is the temperature of helium in each of the states A, B, C and D ?
b. Is there any way of telling afterwards which sample of helium went through the process ABC and which went through the process ADC ? Write yes or no.
How much is the heat involved in each of the process ABC and ADC ?
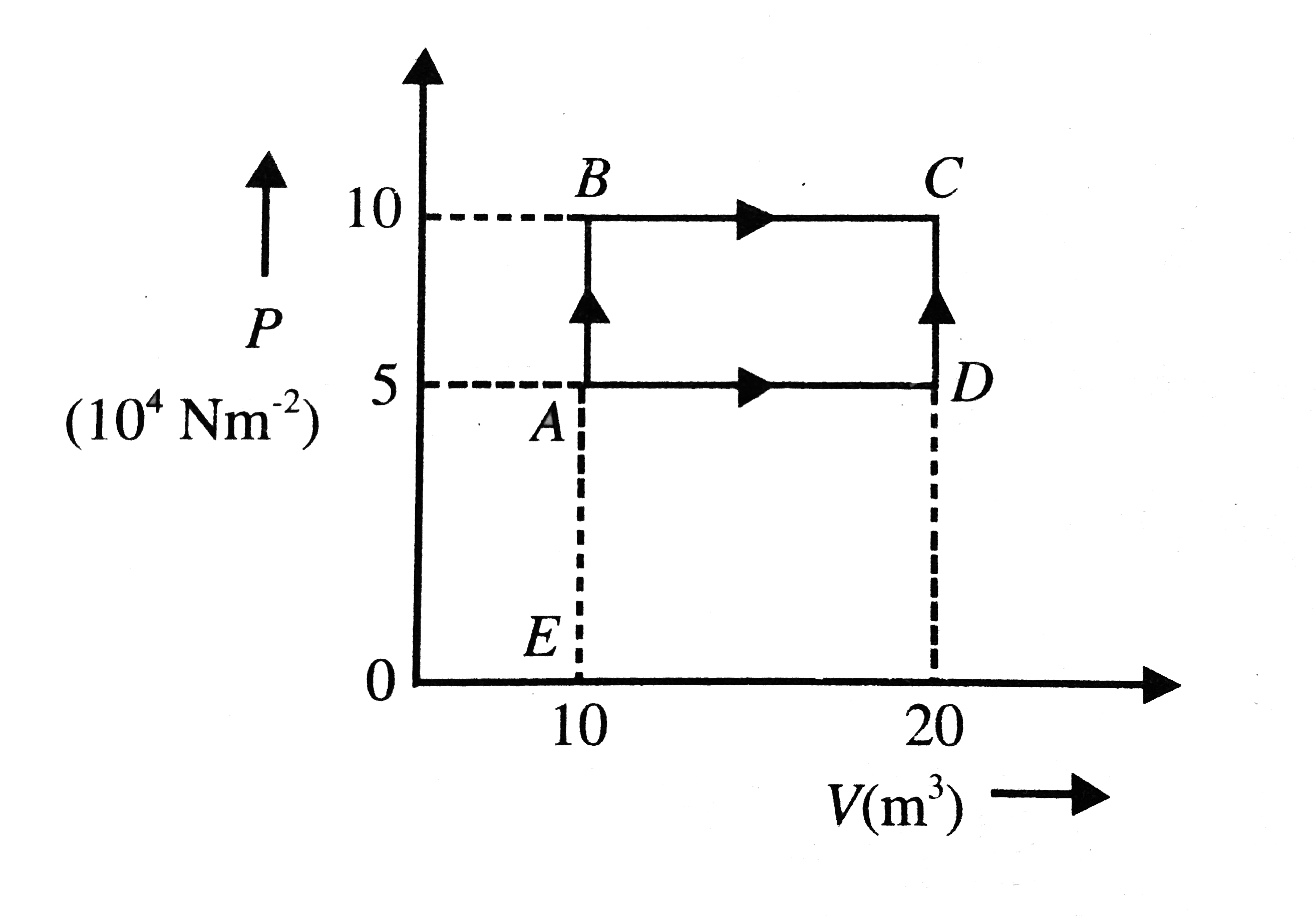
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area `4 xx 10^(-3)m^(2)`. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does `50J` of work in moving the piston through a distance `0.10m`. The temperature of the gas increases by `50K`. Calculate the spring constant and the heat supplied by the heater. `P_(atm) = 1 xx 10^(5)N//m^(2)R = 8.314 J//mol-K`
View SolutionTwo vessels `A` and `B`, thermally insulated, contain an ideal monoatomic gas. A small tube fitted with a value connects these vessels. Initially the vessel `A` has `2` litres of gas at `300K` and `2 xx 10^(5)Nm^(-2)` pressure while vessel `B` has `4` litres of gas at `350K` and `4 xx 10^(5)Nm^(-2)` pressure. The value is now opened and the syetem reaches equilibrium in pressure and temperature. The new pressure will be `(310)/(93) xx 10^(n) (N//m^(2))`. Find `n`.
View SolutionOne mole of a diatomic ideal gas `(gamma = 1.4)` is taken through a cyclic process starting from point A. The process `A to B` is an adiabatic compression. `B to C` is isobaric expansion, `D to A` an adiabatic expansion and is isochoric.
The volume ratio are `V_A //V_B - 16` and `V_C //V_B - 2` and the temperature at `T_A = 300k` is
Find the temperature of the gas at the point (in K).
View SolutionIn the given figure, an ideal gas changes it state from `A` to state `C` by two paths `ABC` and `AC`.
(i) Find the path along which work done is the least.
(ii) The internal energy of the gas at `A` to `10J` and the amount of heat supplied to change its state to `C` through the path `AC` is `200J`. Calculate the internal energy at `C`.
(iii) The internal energy of the gas at state `B` is `30J`. Find the amount of heat supplied to the gas to go from `A to B`.

View SolutionOne mole of an ideal monoatomatic gas is taken round the cylic process `ABCA` as shown Then
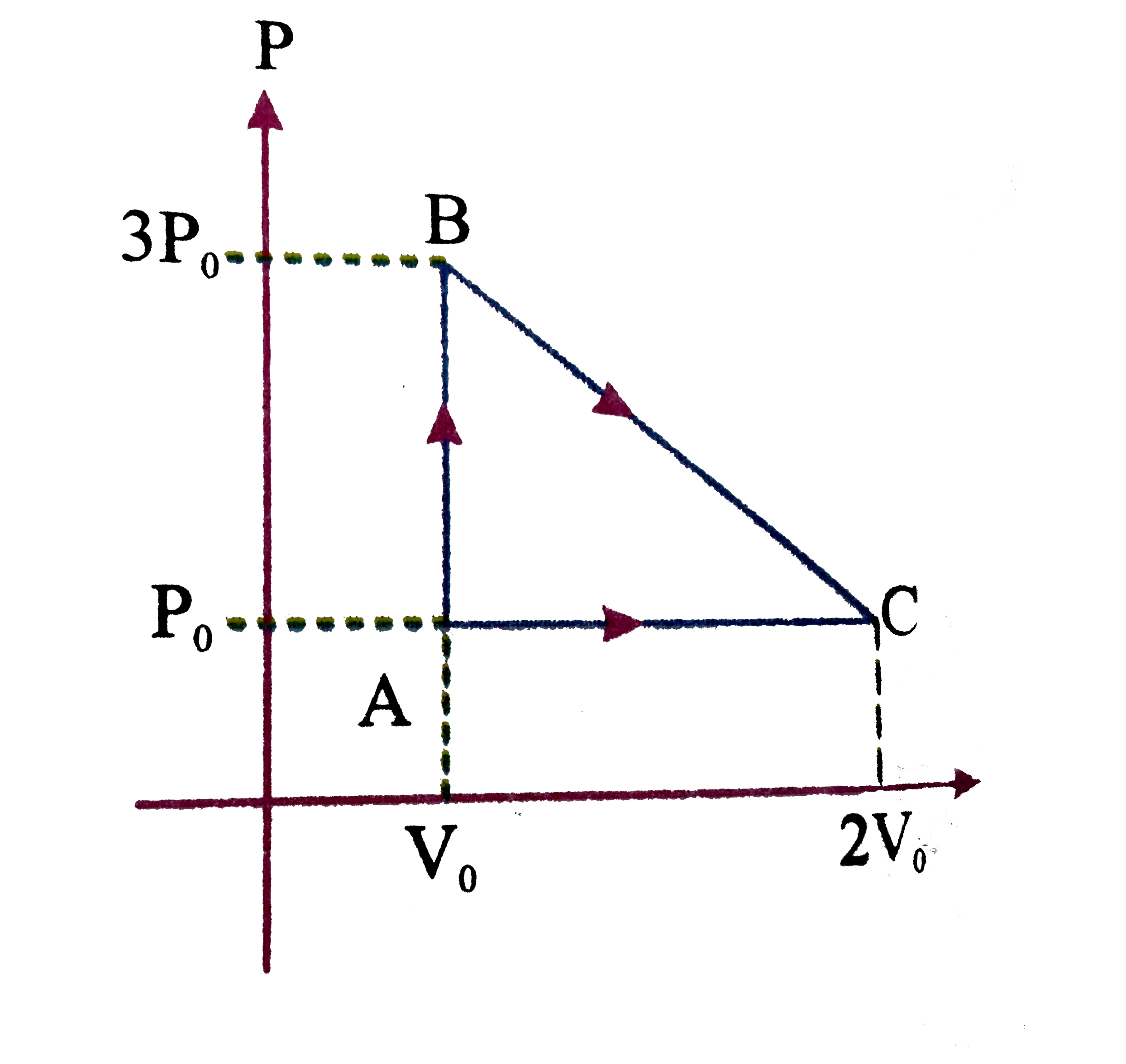
View SolutionTwo moles of an ideal monoatomic gas initially at pressure `P_(1)` and volume `V_(1)` undergo an adiabatic compression until its volume is `V_(2)` . Then the gas is given heat Q at constant volume `V_(2)`.
(i) Sketch the complete process on a `P-V` diagram.
(ii) Find the total work done by the gas, the total change in internal energy and the final temperature of the gas. (Give your answer in terms of `P_(1) , V_(1), V_(2), Q "and" R`)
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes `V` and `3V.2` moles of an ideal gas at pressure `P = 2` atmosphere are confined to the part with volume `V =1` litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, `gamma =1.5`.
View SolutionTwo containers `A` and `B` of equal volume `V_(0)//2` each are connected by a narrow tube which can be closed by a value. The containers are fitted with pistons which can be moved to change the volumes. Initially the value is open and the containers contain an ideal gas `(C_(p)//C_(v)=gamma)` at atmospheric pressure `P_(0)` and atmospheric temperature `2T_(0)`. The walls of the containers `A` are highly conducting and of `B` are non-conducting. The value is now closed and the pistons are slowly pulled out to increase the volumes of the containers to double the original value. (a) Calculate the temperature and pressure in the two containers. (b) The value is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and the pressure.
View SolutionIn given figure, an adiabatic cylindrical tube of volume `2V_(0)` is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure `P_(1)` and temperature `T_(1)` where as in the right side having pressure `P_(2)` and temperature `T_(2).C_(p)//C_(v) =gamma` is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
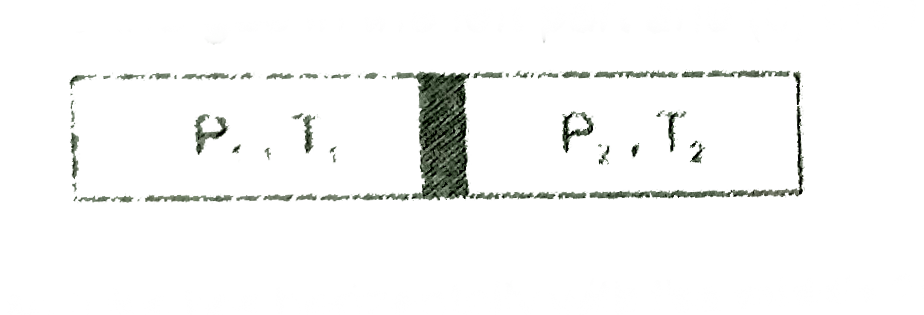
View SolutionIn the given figure a glass tube lies horizontally with the middle `20cm` containing mercury. The two ends of the tube contains air at `27^(@)C` and at a pressure `76 cm` of mercuy. Now the air column on one side in maintained at `0^(@)C` and the other side is maintained at `127^(@)C`. Find the new length of the air column on the cooler side. Neglect the changes in the volume of mercury and of the glass.

View SolutionA cylindrical tube with adiabatic walls having volume `2V_(0)`contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are `P_(0), T_(0)` on the left and `2P_(0), 2T_(0)` on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal

View SolutionA mass of `8g` of oxygen at the pressure of one atmosphere and at temperature `27^(@)C` is enclosed in a cylinder fitted with a frictionless piston. The following operations are performed in the order given (Specific heat fo oxygen `c_(V) = 670 J//kgK`, Molecular mass of oxygen `=32 gm//"mole"`, one atm `= 1.013 xx 10^(5)N//m^(2)` and `R = 25//3 J//"mole"-K)`
(a) the gas is heated at constant pressure to `127^(@)C`,
(b) then it is compressed isothermally to its initial volume and
(c ) finally it is cooled to its initial temperature at constant volume.
View SolutionAn ideal gas `((C_(p))/(C_(v))=gamma)`has initial volume `V_(0)` is kept in a vessel. It undergoes a change and follows the following relation `P = kV^(2)` (where `P` is pressure, and `V` is volume) find the change in internal energy of the gas if its final pressure is `P_(0)`:
View SolutionAn ideal gas `(C_(p)//C_(v) =gamma)` having initial pressure `P_(0)` and volume `V_(0)` (a) The gas is taken isothermally to a pressure `2P_(0)` and then adiabatically to a pressure `4P_(0)`. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure `2P_(0)` and then isothermally to a pressure `4P_(0)`. Find the final volume.
View SolutionAn insulting container of volume `2V_(0)` is divided in two equal parts by a diathermic (conducting) fixed piston. The left part contains one mole of monoatomic ideal gas whereas right part contains two moles of the same gas. Initial pressue on each side is `P_(0)`. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) initial temperature in the two sides, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionAn ideal gas `(gamma=3//2)` is compressed adiabatically form volume `400cm^(3)` to `100cm^(3)`. The initial pressure and temperature are `100 kPa` and `400K`. Find (a) the number of moles of the gas (b) the molar heat capacity at constant pressure, (c ) the final pressure and temperature, (d) the work done by the gas in the process and (e) the change in internal energy of the gas.`(R = (25)/(3)J//mol-k)`
View SolutionTwo samples `A` and `B` of the same gas have equal volumes and pressures . The gas in sample `A` is expanded isothermally to double its volume and the the gas in `B` is expanded adiabatically to double its volume . If the work done by the gas is the same for the two cases, show that gamma satisfies the equation`(1-2 ^(1-gamma))= (gamma - 1 ) 1n2`.
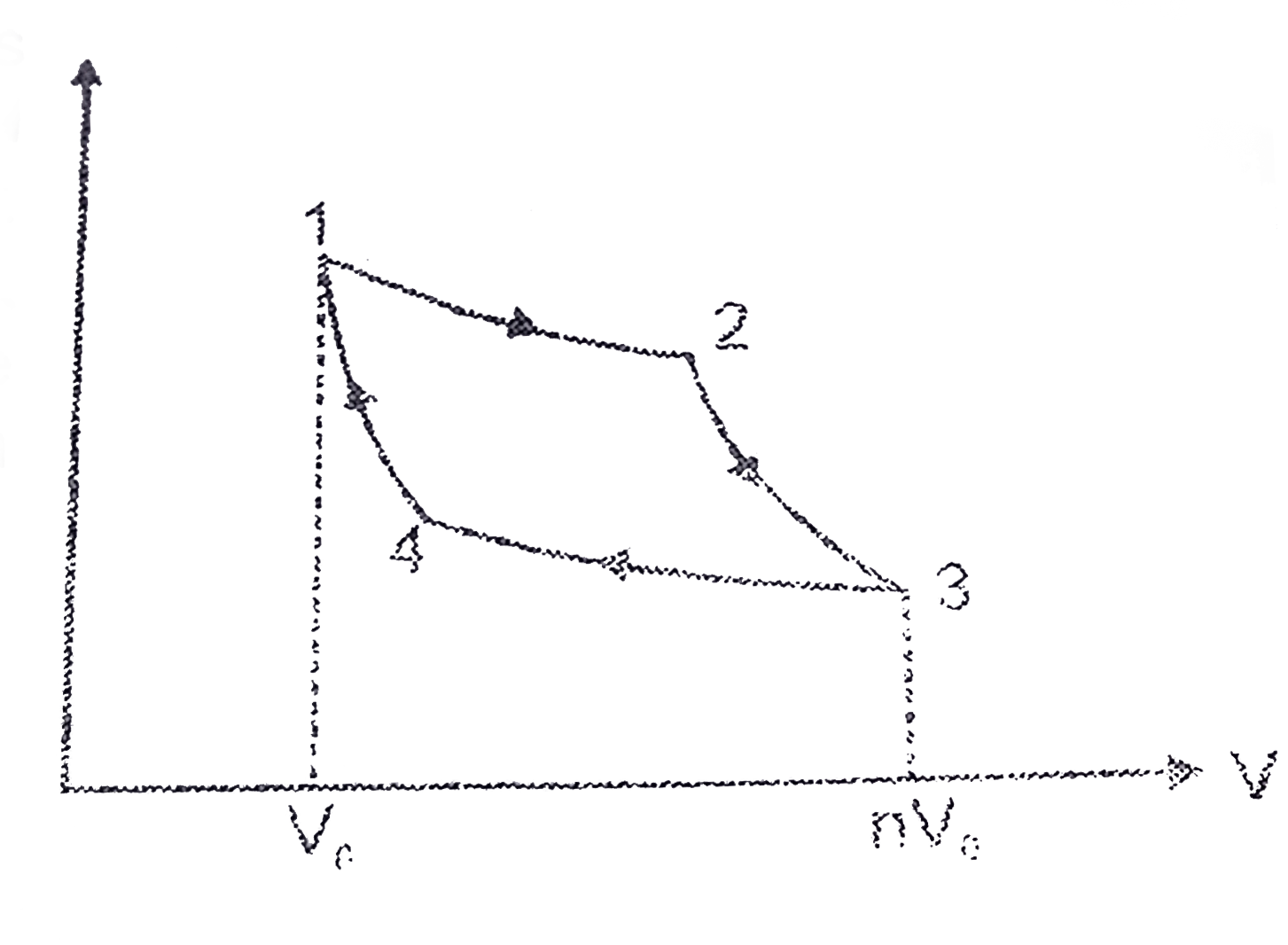
View SolutionA Carnot engine cycle is shown in the Fig. (2). The cycle runs between temperatures `T_(H) = alpha T_(L) = T_(0) (alpha gt T)`. Minimum and maximum volume at state `1` and states `3` are `V_(0)` and `nV_(0)` respectively. The cycle uses one mole of an ideal gas with `C_(P)//C_(V) = gamma`. Here `C_(P)` and `C_(V)` are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters `{alpha, n, T_(0), V_(0) ?}` and universal gas constant `R`.
(a) Find `P, V, T` for all the states
(b) Calculate the work done by the engine in each process: `W_(12), W_(23),W_(34),W_(41)`.
(c) Calculate `Q`, the heat absorbed in the cycle.
View SolutionCloud formation condition
Consider a simplified model of cloub formation. Hot air in contact with the earth's surface contains water vapor. This air rises convectively till the water vapor content reaches its situation pressure. When this happens, the water vpor starts condensing and droplets are formed. We shall estimate the estimate the height a which this happens.We assume that the atmosphere consists of the diatomic gases oxygen and nitrogen in the mass proportion `21:79` respectively. We further assume that the atmosphere is an ideal gas, g the acceleration due to gravity is constant and air processes are adiabatic. Under these assumptions one can show that the pressure is given by
`p = p_(0) ((T_(0)-T_(z))/(T_(0)))^(alpha)`
Here `p_(0)` and `T_(0)` is the pressure and temperature respectively at seal level `(z = 0),T` is the lapse rate (magnitude of the change in temperature `T` with height `z` abive the earth's surface, i.e. `T gt 0)`.
View Solution
SUBJECTIVE QUESTIONS questions and complete solutions for chapter KTG & THERMODYNAMICS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS KTG & THERMODYNAMICS
- Advancel Level Problems
- Board Level Exercise
- Examples
- Exercise -1
- Exercise-2
- Exercise-3
- PART - I
- PART - II
- PART -I
- PART -II
- PART -III
- PART -IV
- Problem
- SECTION
- SECTION (A)
- SECTION (B)
- SECTION (C)
- SECTION (D)
- SECTION (E)
- SECTION (F)
- SECTION (G)
- SECTION (H)
- SECTION (I)
- SECTION (J)
- Solved Examples
- Solved problem
- SUBJECTIVE QUESTIONS