Complete Solutions to dpp 49 of chapter DAILY PRACTICE PROBLEMS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DAILY PRACTICE PROBLEMS |
| RESONANCE | dpp 49 |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
A bob is attached to one end of a string other end of which is fixed at ped `A`. The bob is taken to a position where string makes an angle of `30^(@)` with the horizontal. On the circular path of the bob in vertical plane there is a peg` 'B'` at a symmetrical position with respect to the position of release as shown in the figure. If `V_(c)` and `V_(a)` be the minimum speeds in clockwise and anticlokwise direction respectively, given to the bob in order to hit the peg `'B'` then ratio `V_(c) : V_(a)` is equal to `:`

View SolutionA ring of radius `R` lies in vertical plane. A bead of mass `'m'` can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed `v` with which the ring must be pulled such that the bead completes the vertical circle.
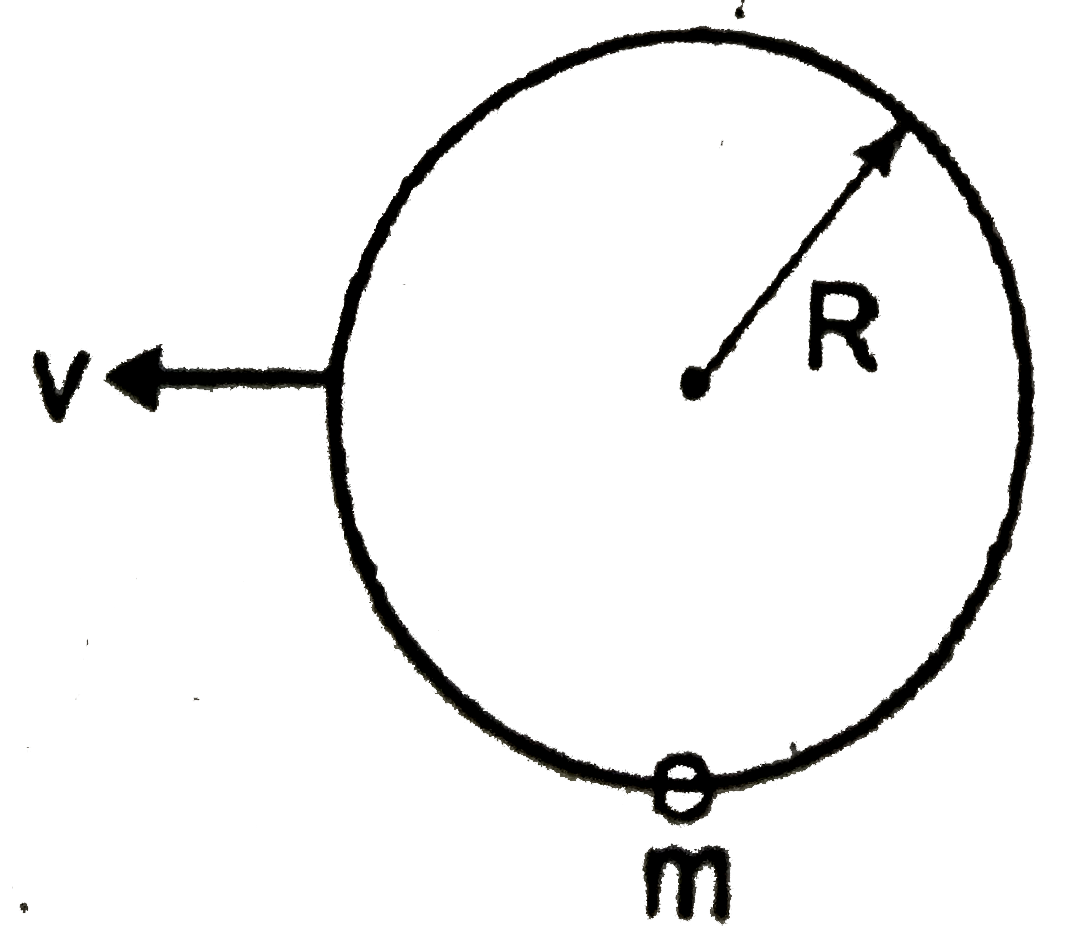
View SolutionAn object is moving in a circle at constant speed `v`. The magnitude of rate of change of momentum of the object.
View SolutionAssuming potential energy 'U' at ground level to be zero.
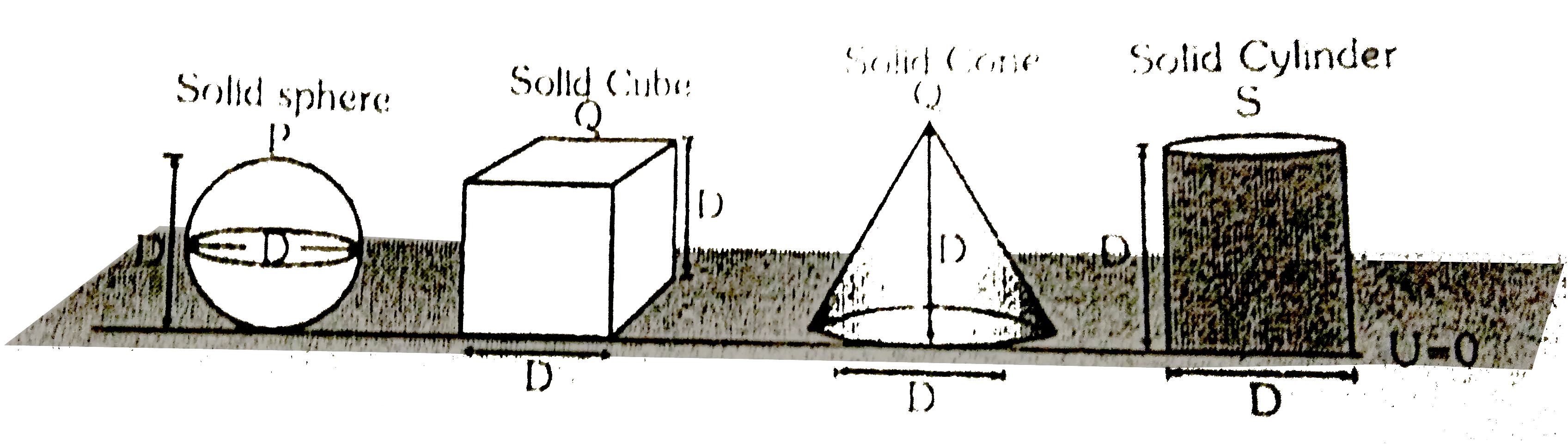
All objects are made up of same material :-
`{:(U_(P) = "Potential energy of solid sphere",U_(Q) = "Potential energy of solid cube",),(U_(R ) = "Potential energy of solid cone",U_(S) = "Potential energy of solid cylinder",):}`
View SolutionA bob of mass `2kg` is suspended from point `O` of a core with an inextensible string strinng of length `sqrt(3)m`. It is moving in horizontal circle over the surface of cone as shown in the figure. Then `:(g=10m//s^(2))`
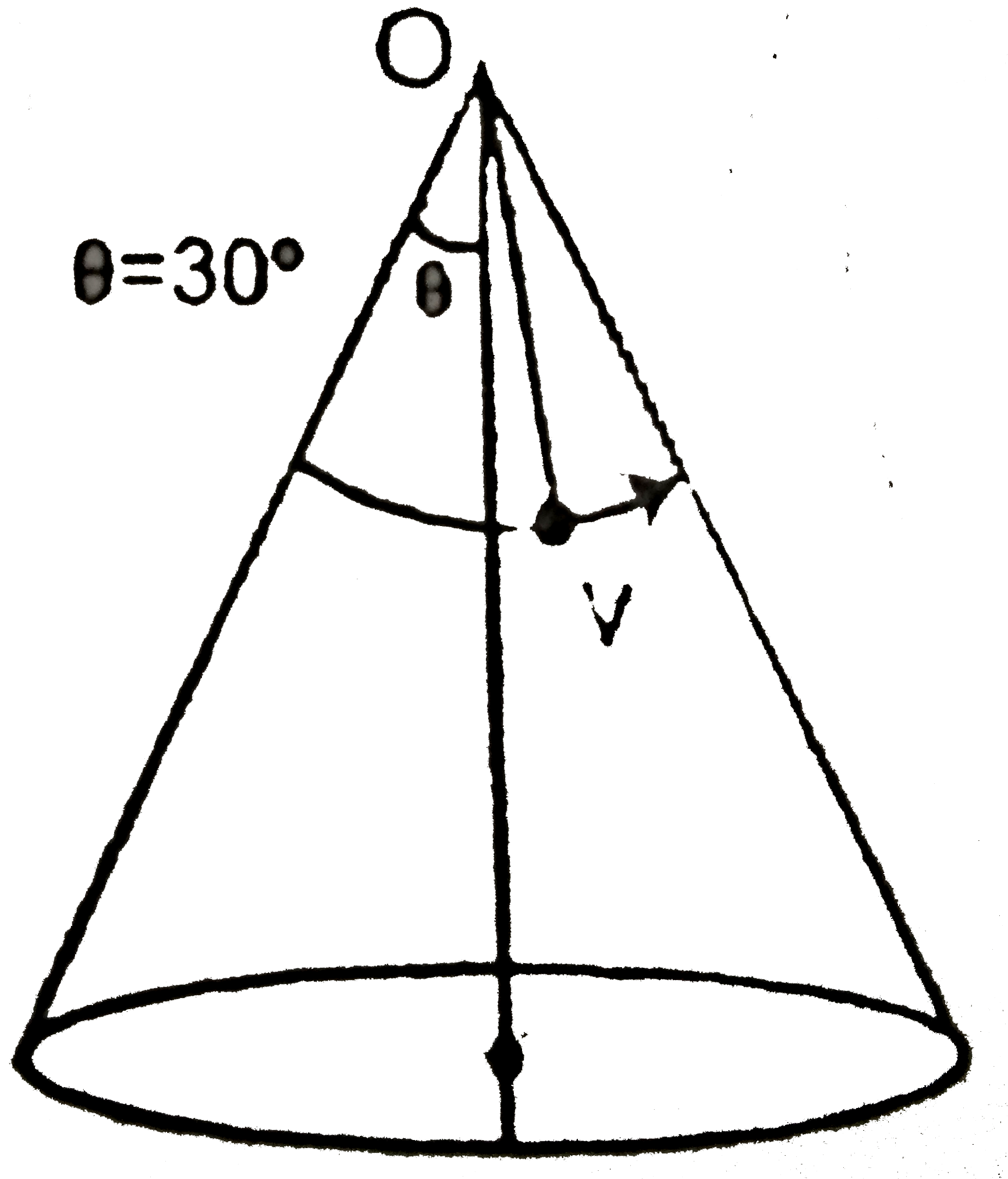
View SolutionA block of mass `m` rests on a rough horizontal plane having coefficient of kinetic friction `mu_(k)` and coefficient of static friction `mu_(s)`. The spring is in its natural, when a constant force of magnitude `P=(5mu_(k)mg)/(4)` starts acting on the block. The spring force `F` is a function of extension `x` as `F=kx^(2).(` Where `k` is spring constant `)`

`(a)` Comment on the relation between `mu_(s)` and `mu_(k)` for the motion to start.
`(b)` Find the maximum extension in the spring `(` Assume the force `P` is sufficient make the block move `)`.
View Solution
dpp 49 questions and complete solutions for chapter DAILY PRACTICE PROBLEMS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS DAILY PRACTICE PROBLEMS
- comprehension
- Compreshension
- dpp 15
- dpp 16 physics
- dpp 17
- dpp 18
- dpp 19
- dpp 2 PHYSICS
- dpp 20
- dpp 21
- dpp 22.
- dpp 24
- dpp 25
- dpp 26
- dpp 27
- dpp 28
- dpp 30
- dpp 31
- dpp 32
- dpp 33
- dpp 34
- DPP 35
- dpp 36
- Dpp 37
- dpp 38
- dpp 39
- dpp 40
- dpp 41
- dpp 42
- dpp 43
- dpp 44
- DPP 45
- dpp 46
- dpp 47
- dpp 48
- dpp 49
- DPP 50
- dpp 51
- dpp 52
- dpp 53
- dpp 54
- DPP 55
- dpp 56
- dpp 57
- dpp 58
- dpp 59
- dpp 60
- DPP 62
- dpp 63
- dpp 64
- DPP 65
- dpp 66
- dpp 67
- dpp 68
- dpp 69
- dpp 70
- dpp 71
- dpp 72
- dpp 74
- dpp 75
- dpp 76
- DPP 77
- dpp 78
- dpp 79
- DPP 8 PHYSICS
- dpp 80
- dpp 81
- dpp 82
- dpp 83
- dpp 84
- dpp 85
- dpp 86
- dpp 87
- dpp 88
- dpp 89 illustration
- dpp 90 Illustration
- dpp 91 illustration
- dpp 92 illustration
- Dpp no 10 physics
- Dpp no 11 physics
- Dpp no 12 Physics
- Dpp no 6 physics
- DPP NO 7 PHYSICS
- DPP no 9 physics
- Dpp no. 13 physics
- DPP NO. 14 PHYSICS
- DPP NO. 5 Physics
- dpp23
- dpp29
- dpp61
- dpp73
- Now answer the following :
- PHYSICS
- TRUE/FALSE