Complete Solutions to comprehension of chapter DAILY PRACTICE PROBLEMS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DAILY PRACTICE PROBLEMS |
| RESONANCE | comprehension |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If a man has a velocity varying with time given as `v=3t^(2),v` is in `m//s` and `t` in `sec` then `:`

Find out the velocity of the man after `3 sec`.
View SolutionIf a man has a velocity varying with time given as `v=3t^(2),v` is in `m//s` and `t` in `sec` then `:`

Find out his displacement after 2 seconds of his start `:`
View SolutionIf a man has a velocity varying with time given as `v=3t^(2),v` is in `m//s` and `t` in `sec` then `:`

Find out his acceleration after 3 seconds `:`
View SolutionPosition vector `vec(A)` is `2hat(i)`
Position vector `vec(B0` is `3hat(j)`
`hat(i),hat(j),hat(k)` are along the shown `x,y,` and `z` is

Geometrical representation of `vec(A)` is
View SolutionPosition vector `vec(A)` is `2hat(i)`
Position vector `vec(B0` is `3hat(j)`
`hat(i),hat(j),hat(k)` are along the shown `x,y,` and `z` is

Geometrical representation of `vec(B)` is `:`
View SolutionPosition vector `vec(A)` is `2hat(i)`
Position vector `vec(B0` is `3hat(j)`
`hat(i),hat(j),hat(k)` are along the shown `x,y,` and `z` is
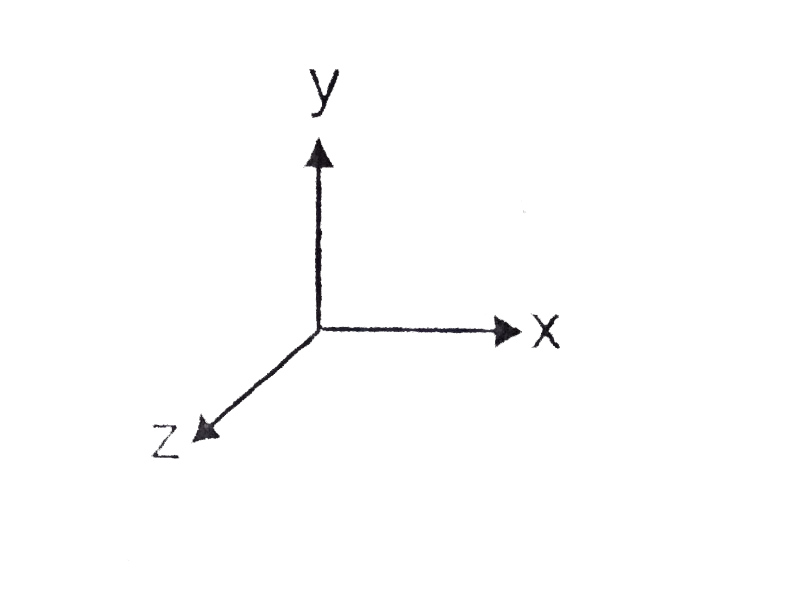
`-4 vec(A)` can be represented as
View SolutionThe velocity `'v'` of a particle moving along straight line is given in terms of time `t` as `v=3(t^(2)-t)` where `t` is in seconds and `v` is in `m//s`.
The distance travelled by particle from `t=0` to `t=2 `seconds is `:`
View SolutionThe velocity `'v'` of a particle moving along straight line is given in terms of time `t` as `v=3(t^(2)-t)` where `t` is in seconds and `v` is in `m//s`.
The displacement of aprticle from `t=0` to `t=2` seconds is `:`
View SolutionThe velocity `'v'` of a particle moving along straight line is given in terms of time `t` as `v=3(t^(2)-t)` where `t` is in seconds and `v` is in `m//s`.
The speed is minimum after `t=0` second at instant of time
View SolutionA bus is moving rightward with a velocity of `15m//sec` and on the bus a monkey is renning oppositely with a velocity of `5m//sec(` with respect to the bus `)`. Nearby a helicopter is rising vertically up with a velocity of `10m//sec.`

Find out the direction of the helicopter as seen by the monkey.
View SolutionA bus is moving rightward with a velocity of `15m//sec` and on the bus a monkey is renning oppositely with a velocity of `5m//sec(` with respect to the bus `)`. Nearby a helicopter is rising vertically up with a velocity of `10m//sec.`

Find out the direction of the bus as seen by the helicopter's pilot.
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with `x-` and `y-` components as shown. After time `t=5` , the particle has no acceleration.

What is the magnitude of velocity of the particle at `t=2` seconds ?
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with x- and y- components as shown. After time t=5 , the particle has no acceleration.
What is the magnitude of average velocity of the particle between t=0 and t=4 seconds ?
A. `(5)/(2)sqrt(13)m//s`
B. `(5)/(2)sqrt(17)m//s`
C. `30m//s`
D. None of these
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with `x-` and `y-` components as shown. After time `t=5` , the particle has no acceleration.

When is the particle at its farthest distance from the `y-` axis ?
A. 3 sec.
B. 2 sec.
C. 4 sec.
D. 1 sec.
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
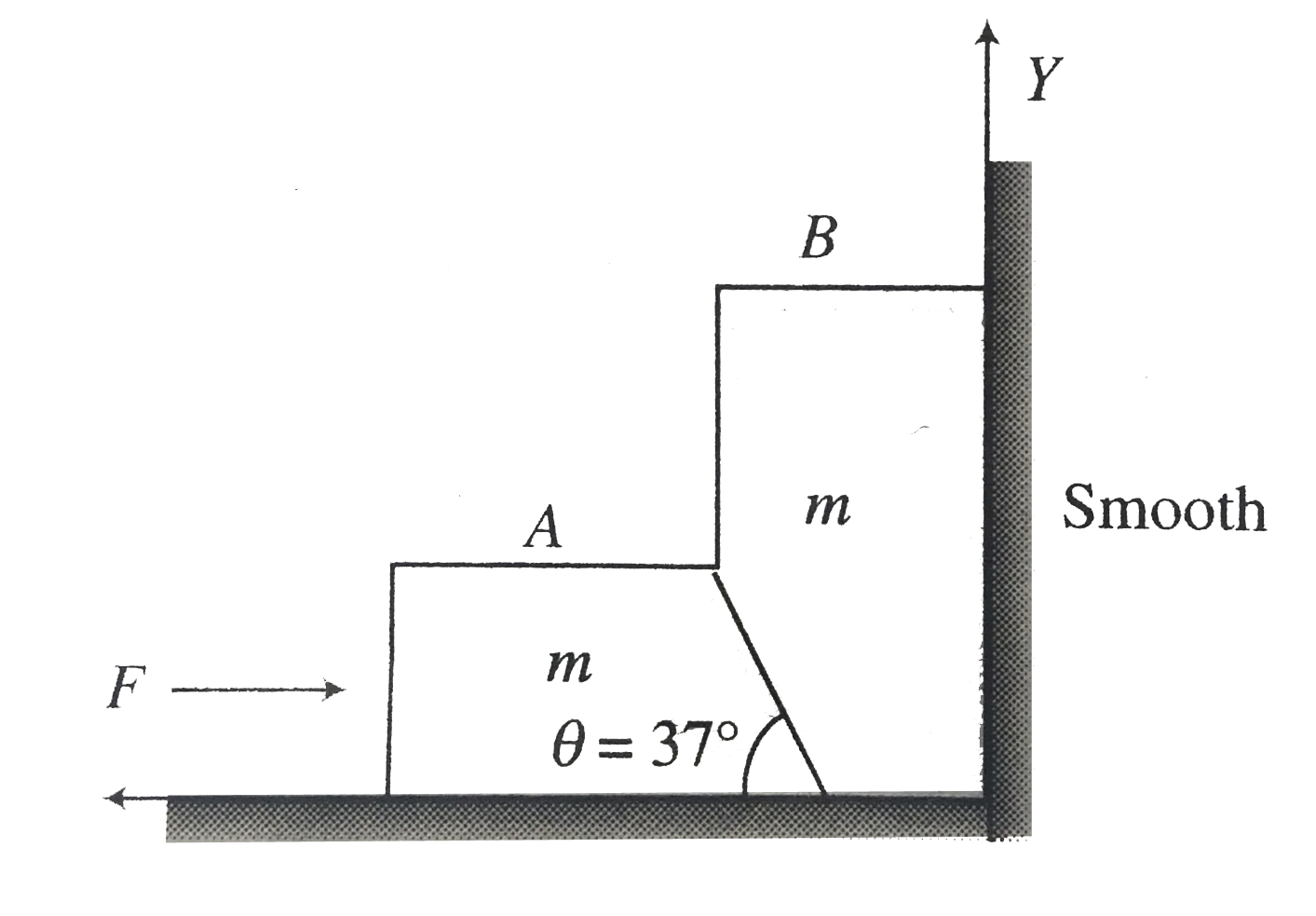
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
What is the minimum value of F to lift block B from ground?
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
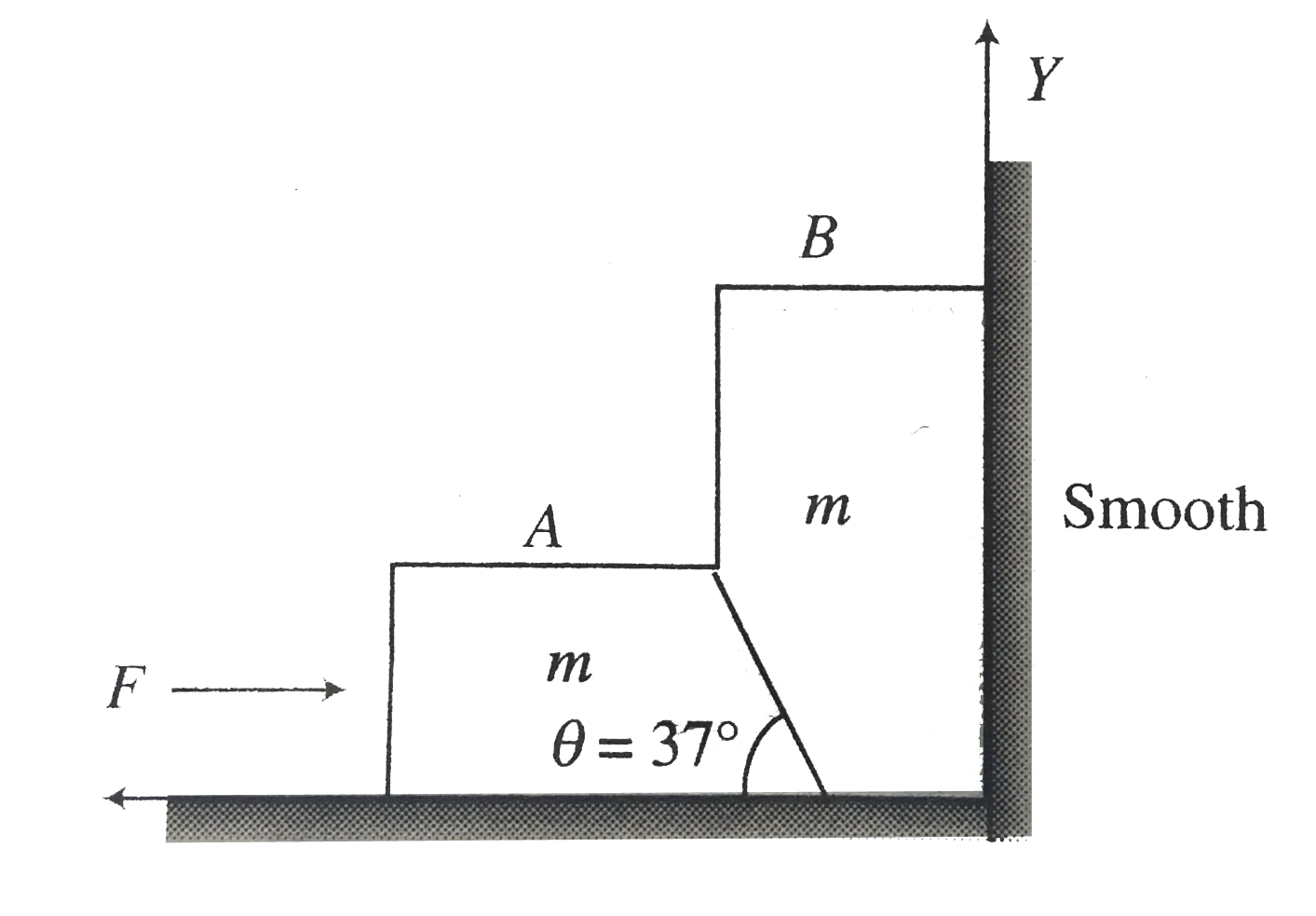
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If both the blocks are stationary, the force exerted by ground of block A is
View SolutionTwo smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases `F(theta = 37^(@)` with horizontal).
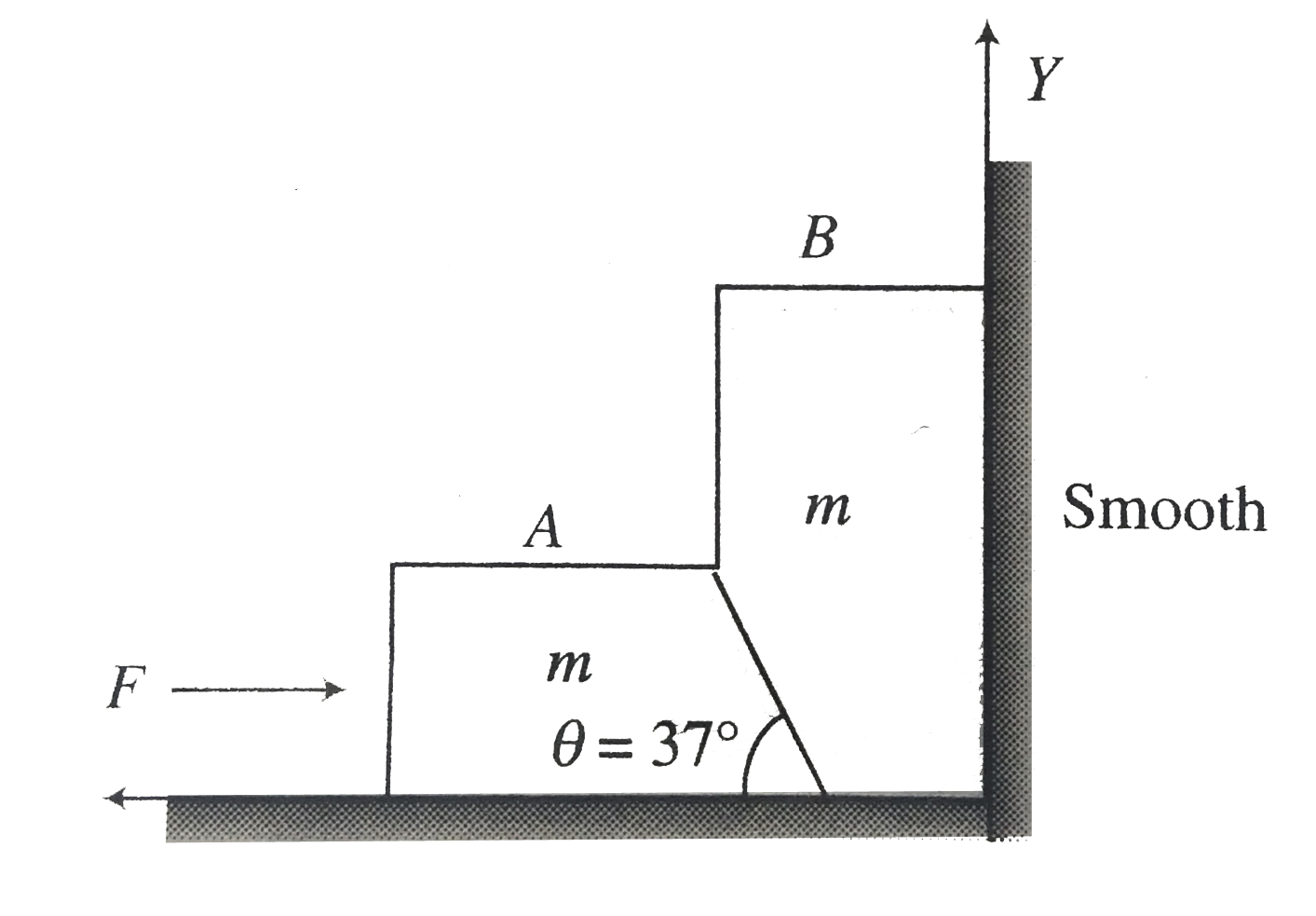
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If the acceleration of block A is a rightwards, then the acceleration of block B will be
View SolutionA meter stick `AB` of length 1 meter rests on a frictionless floor in horizontal position with end `A` attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
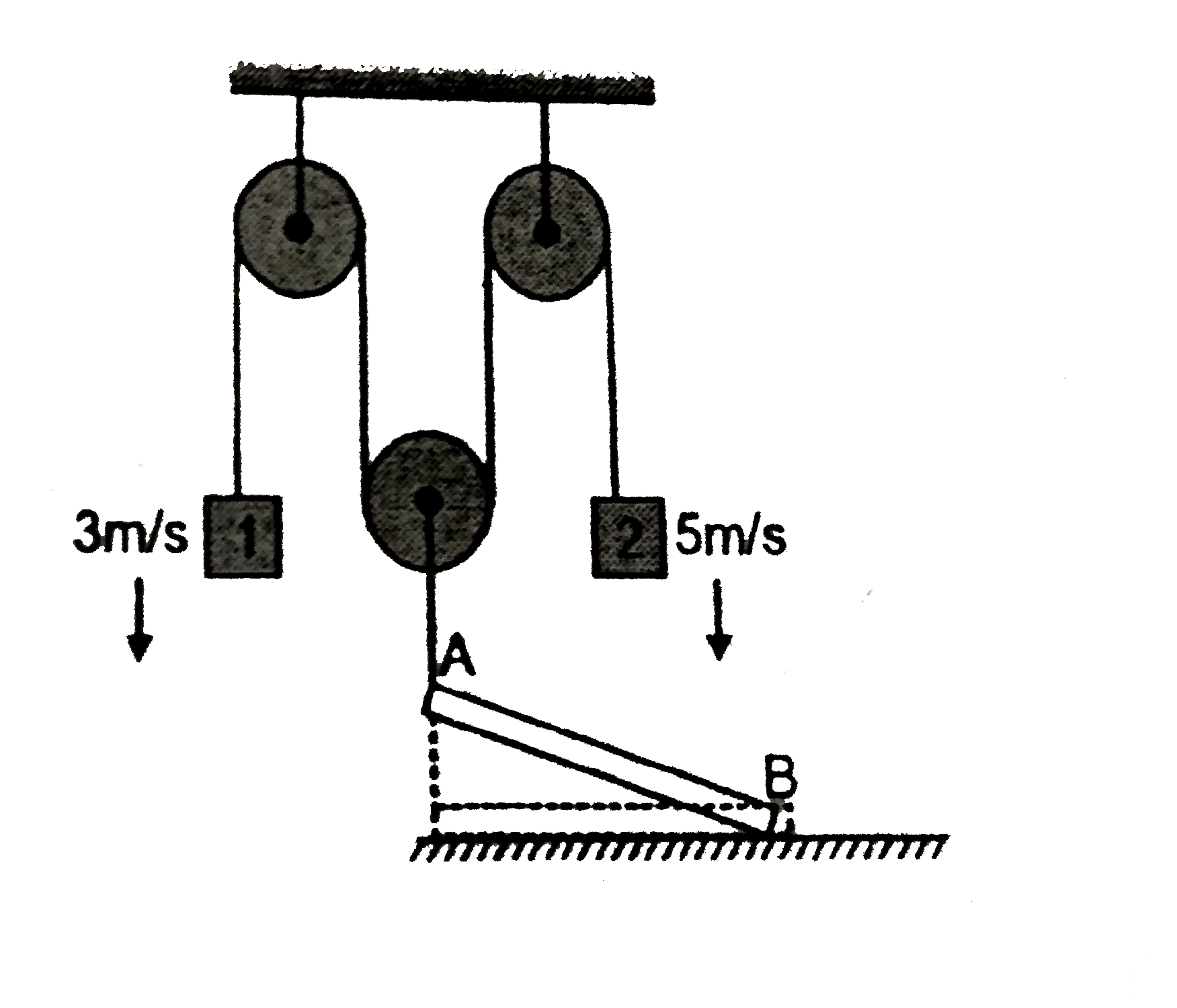
If block 1 and 2 are given constant speeds as shown then the distance moved by end `B` over the floor in the period for which speed of `B` is less than `A`.
View SolutionA meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
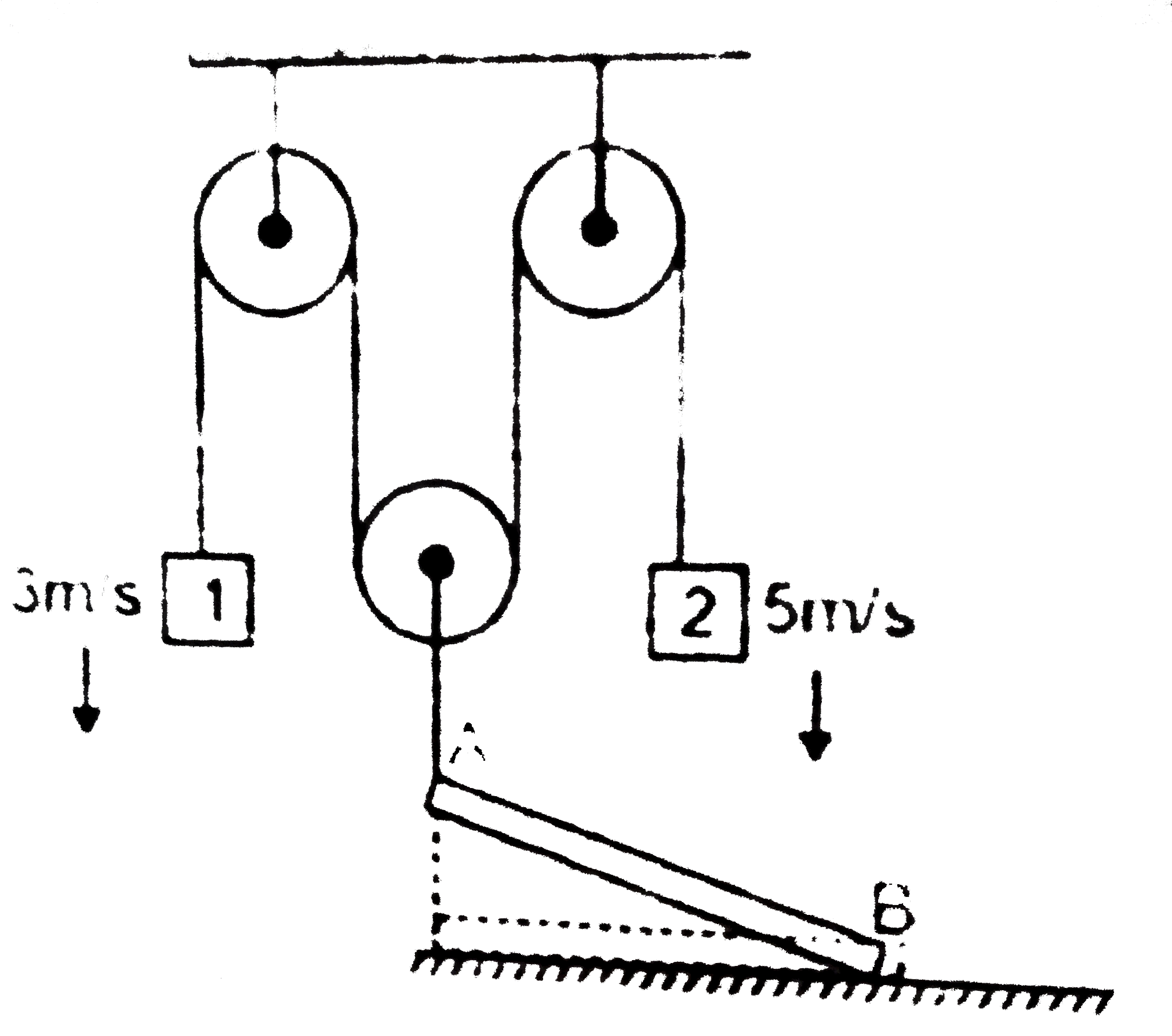
Time taken to cover the distance in above part is :
View SolutionA meter stick `AB` of length 1 meter rests on a frictionless floor in horizontal position with end `A` attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Minimum magnitude of relative velocity of `A` with respect to `B` during the motino specified in question 5 is `:`
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.
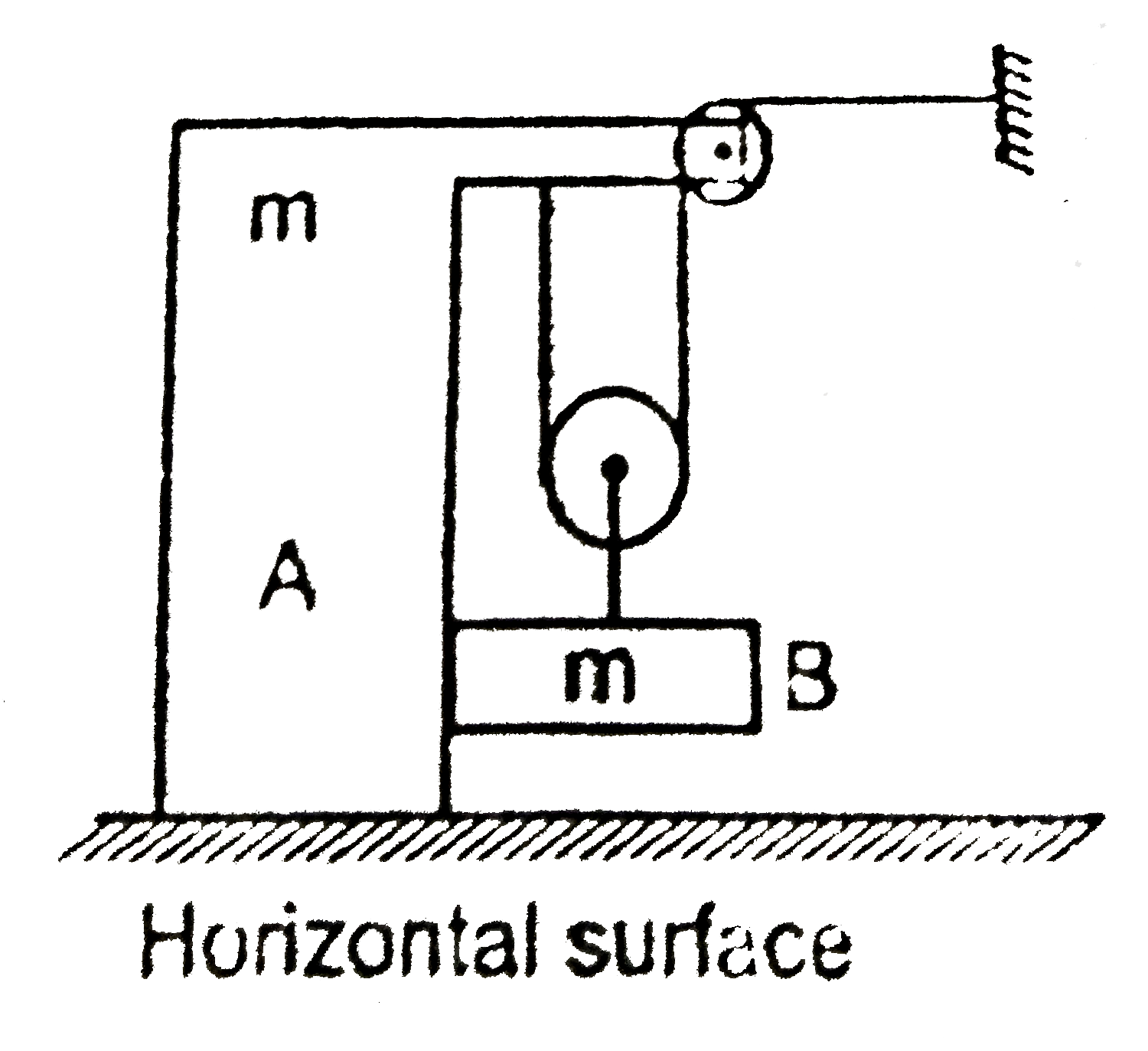
The acceleration of block `A` is `:`
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.

Normal reaction between `A` and ground is `:`
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.

Normal reaction between `A` and `B` is `:`
View Solution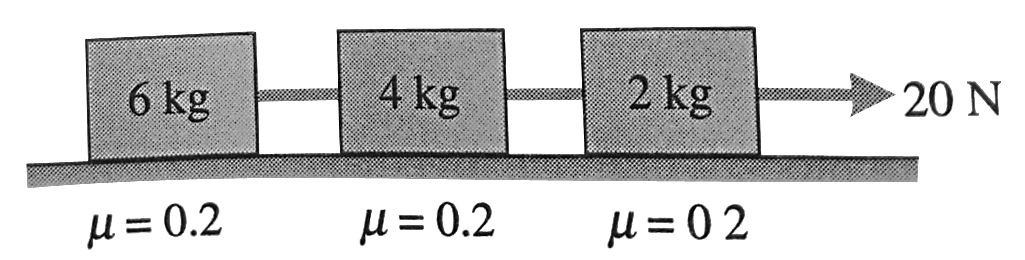
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View Solution
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. Friction force on 4 kg block is
View Solution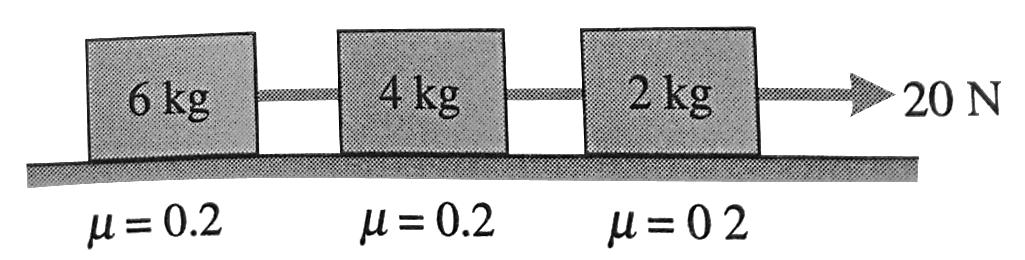
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. Friction force on 6 kg block is
View Solution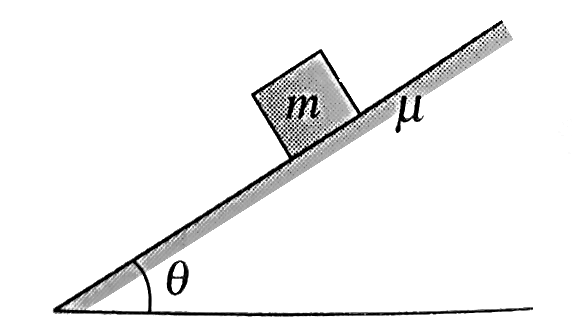 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If `mu=(3)/(4)` then what will be frictional force (shear force) acting between the block and inclined plane when `theta=30^@`:
View Solution A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If `mu=(3)/(4)` then what will be frictional force (shear force) acting between the block and inclined plane when `theta=30^@`:
View Solution A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is `mu` and the inclination of the plane is `theta`.Initially `theta=0` and the block will remain stationary on the plane. Now the inclination `theta` is gradually increased . The block presses theinclined plane with a force `mgcostheta`. So welding strength between the block and inclined is `mumgcostheta`, and the pulling forces is `mgsintheta`. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle `theta` for which the block start sliding is called angle of repose `(lamda)`. During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If `mu=(3)/(4)` then what will be frictional force (shear force) acting between the block and inclined plane when `theta=30^@`:
View SolutionRain is falling with a velocity `(-4hat(i)+8hat(j)-10hat(k))`. A person is moving with a velocity of `(6hat(i)+8hat(j))` on the ground.
Find the velocity of rain with respect to man and the direction from which the rain appears to be coming.
View SolutionRain is falling with a velocity `(-4hat(i)+8hat(j)-10hat(k))`. A person is moving with a velocity of `(6hat(i)+8hat(j))` on the ground.
The speed with the rain drops hit the person is `:`
View SolutionRain is falling with a velocity `(-4hat(i)+8hat(j)-10hat(k))`. A person is moving with a velocity of `(6hat(i)+8hat(j))` on the ground.
Find the velocity of rain with respect to man and the direction from which the rain appears to be coming.
View SolutionA block of mass `1kg `is placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by `x(x ge (mumg)/(k))`. Let `F_(max)` and `F_(mi n)` be the maximum and minimum values of force `F` for which the block remains in equilibrium. For a particular `x, F_(max)-F_(mi n)=2N`. Also shown is the variation of `F_(max)+F_(mi n)` versus `x`, the elongation of the spring.
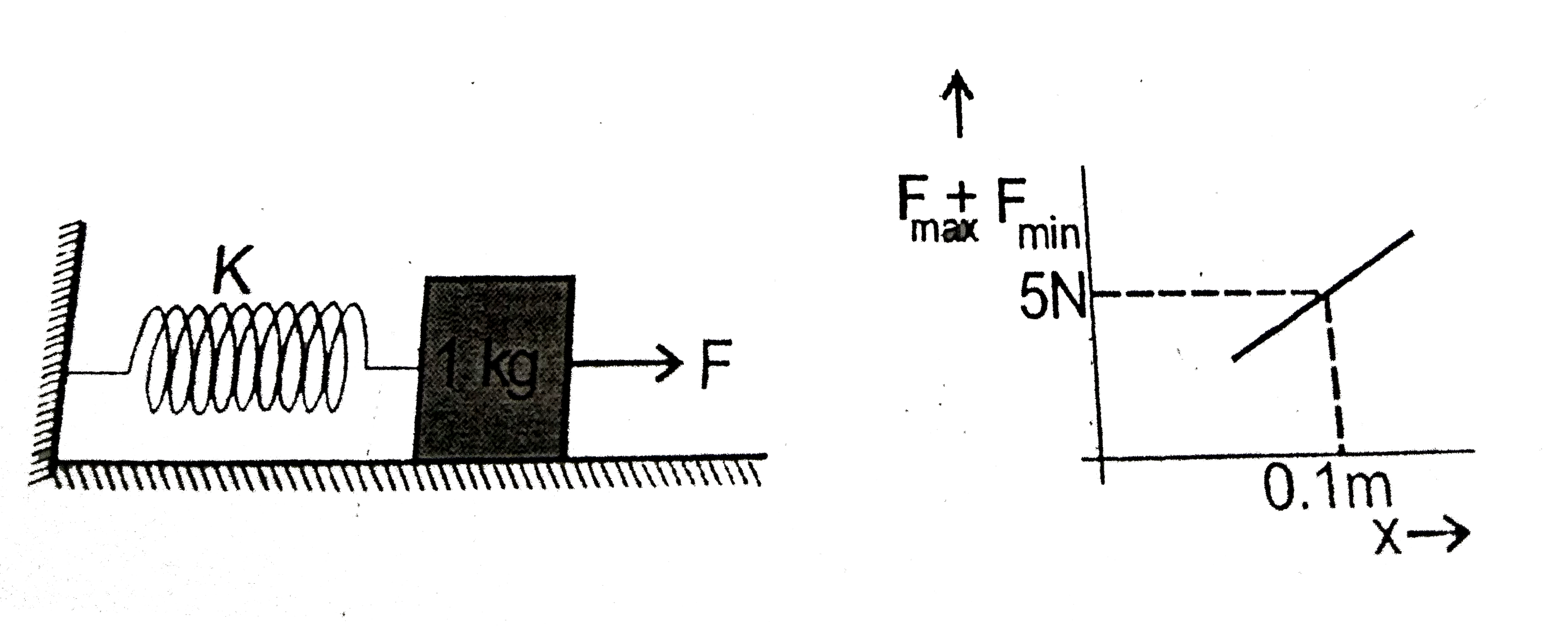
The coefficient of friction between the block and the horizontal surface is `:`
View SolutionA block of mass `1kg `is placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by `x(xge(mumg)/(k))`. Let `F_(max)` and `F_(mi n)` be the maximum and minimum values of force `F` for which the block remains in equilibrium. For a particular `x, F_(max)-F_(mi n)=2N`. Also shown is the variation of `F_(max)+F_(mi n)` versus `x`, the elongation of the spring.
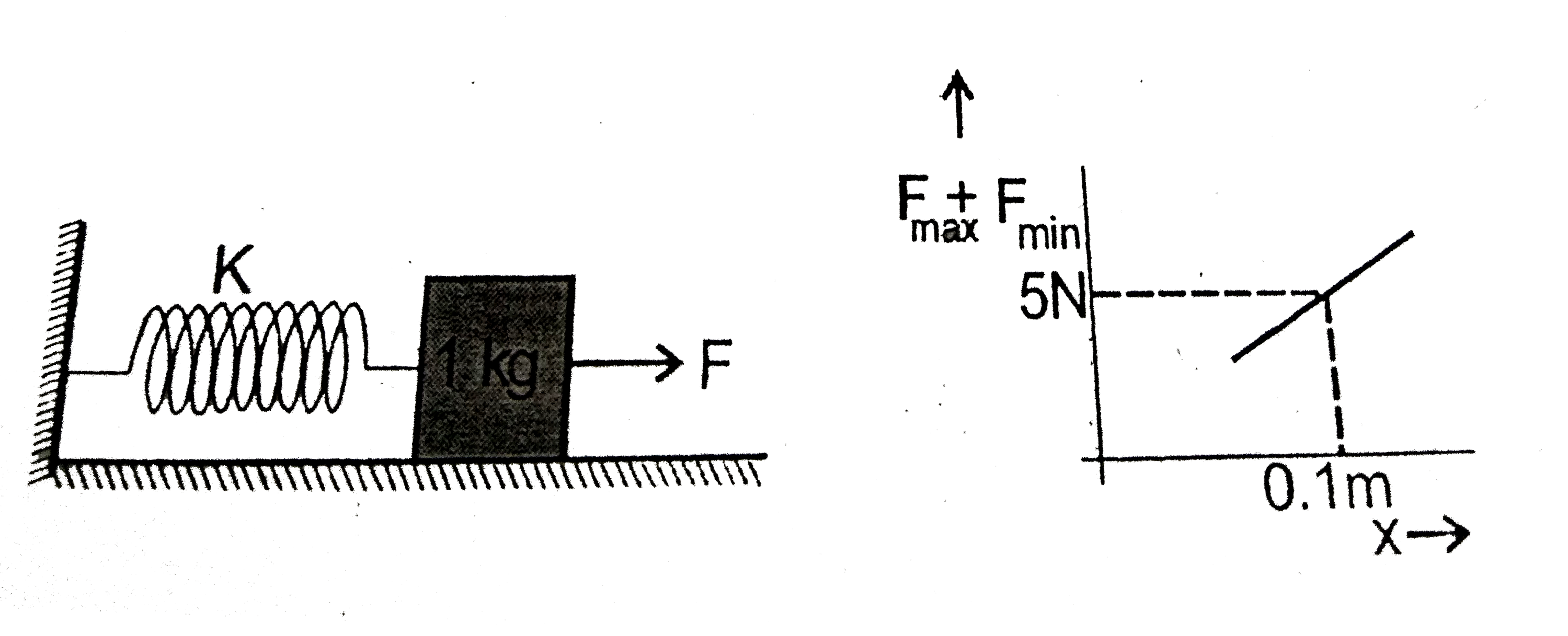
The spring constant of the spring is `:`
View SolutionA block of mass `1kg `is placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by `x(x ge (mumg)/(k))`. Let `F_(max)` and `F_(mi n)` be the maximum and minimum values of force `F` for which the block remains in equilibrium. For a particular `x, F_(max)-F_(mi n)=2N`. Also shown is the variation of `F_(max)+F_(mi n)` versus `x`, the elongation of the spring.
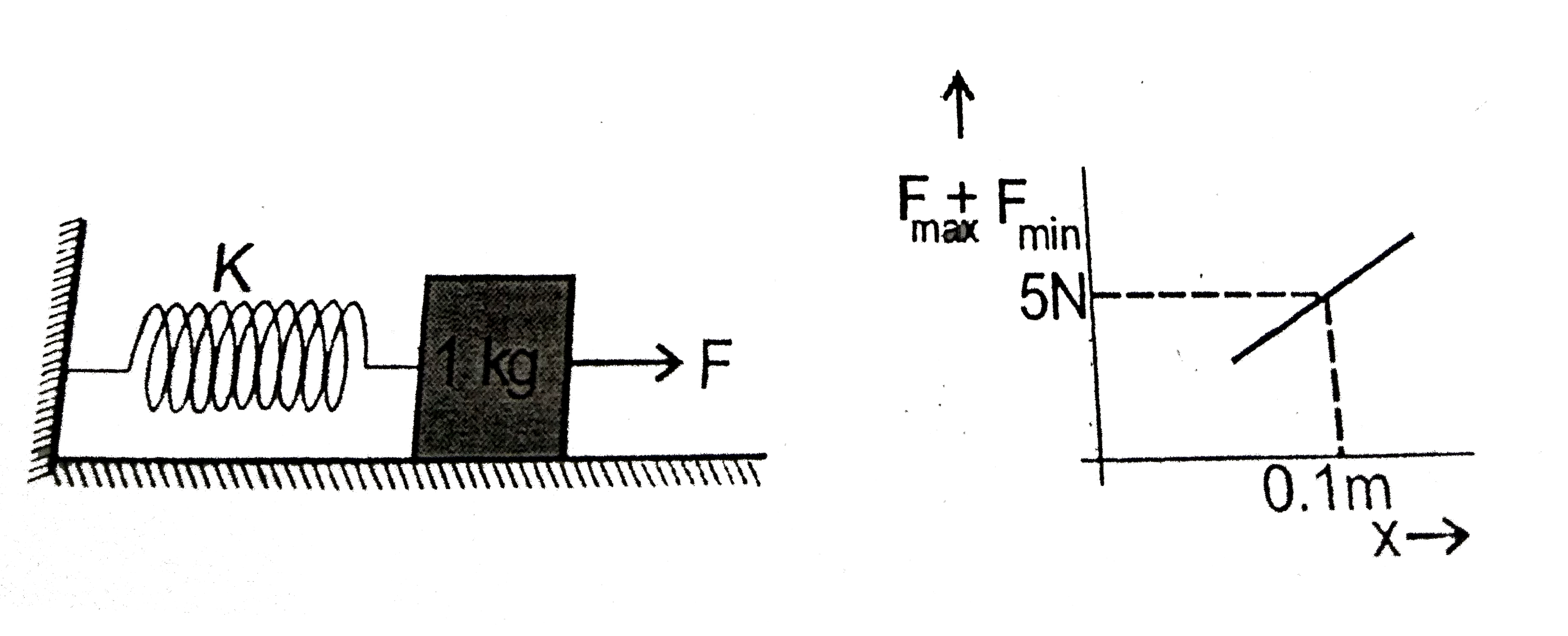
The value of `F_(mi n)`, if `x=3cm` is `:`
View SolutionConsider the system shown below, with two equal masses `m` and a spring with spring constant `K`. The coefficient of friction between the left mass and horizontal table is `mu=1//4`, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
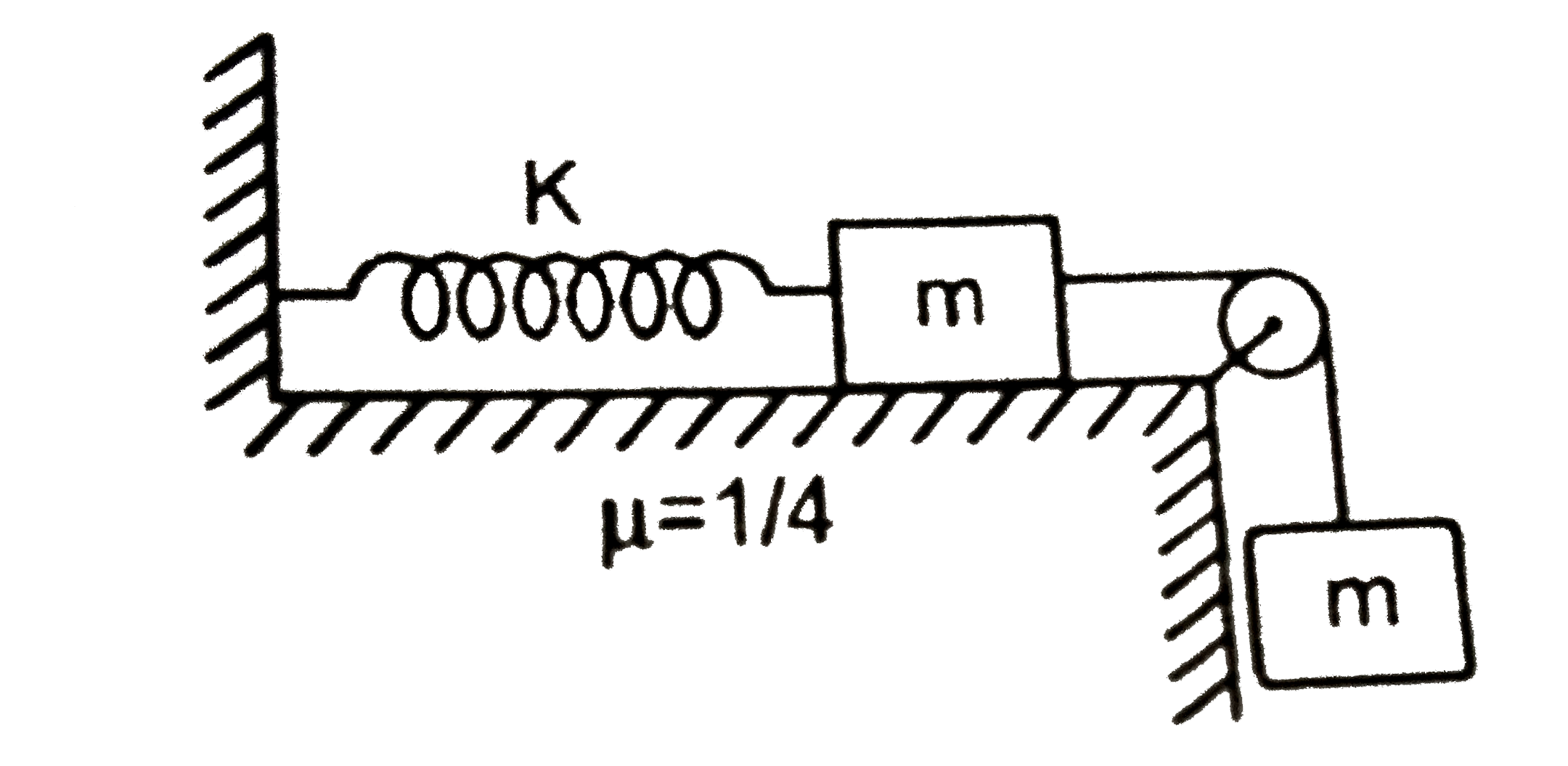
The extension in spring when the masses come to momentary rest for the first time is
View SolutionConsider the system shown below, with two equal masses `m` and a spring with spring constant `K`. The coefficient of friction between the left mass and horizontal table is `mu=1//4`, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.

The extension in spring when the masses come to momentary rest for the first time is
View SolutionConsider the system shown below, with two equal masses `m` and a spring with spring constant `K`. The coefficient of friction between the left mass and horizontal table is `mu=1//4`, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.

The extension in spring when the masses come to momentary rest for the first time is
View SolutionA small block of mass `m` is released from a fixed smooth wedge in figure. Initial point is marked as `A`. Bottom of wedge is marked as `B` and at a point `C` the block stops because the straight part of floor is rough.

Work donw by normal reaction is zero during the motion of the block
View SolutionA small block of mass `m` is released from a fixed smooth wedge in figure. Initial point is marked as `A`. Bottom of wedge is marked as `B` and at a point `C` the block stops because the straight part of floor is rough.

The friction coefficient of the block with the floor is `:`
View SolutionA small block of mass `m` is released from a fixed smooth wedge in figure. Initial point is marked as `A`. Bottom of wedge is marked as `B` and at a point `C` the block stops because the straight part of floor is rough.
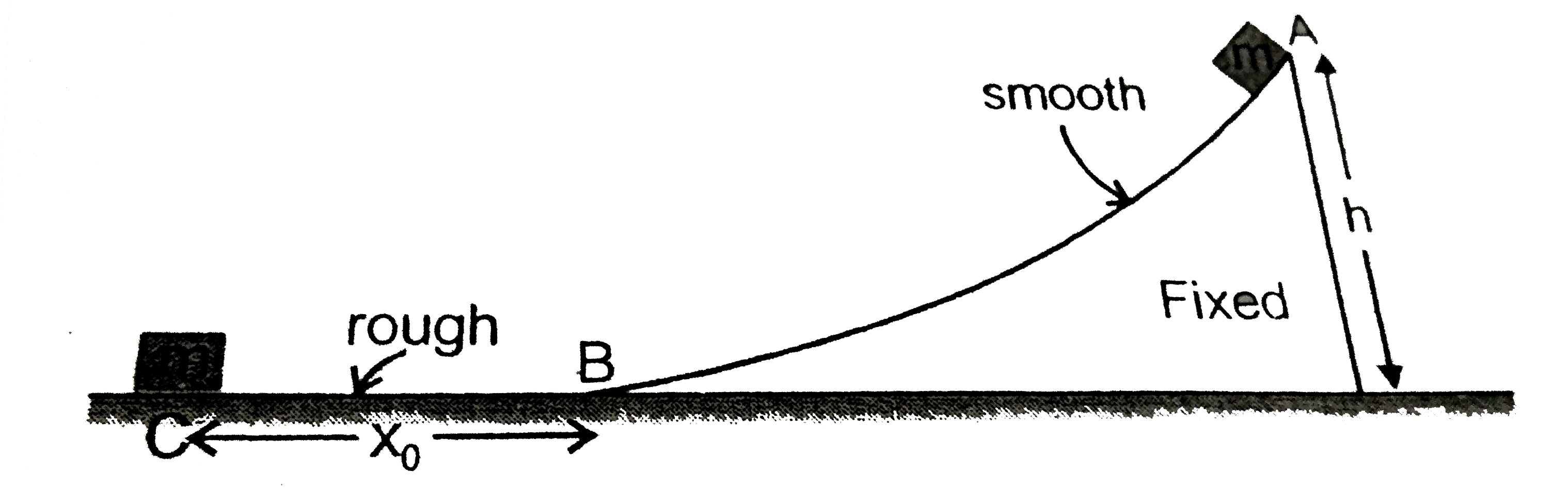
The velocity of the block at the midpoint between `B` to `C` will be `:`
View SolutionA particle of mass `0.1kg` is launched at an angle of `53^(@)` with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than `12.5m` and which is inclined at an angle of `37^(@)` with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is `mu=(3)/(8)[` Take `g=10m//g^(2)]`

The velocity of the particle as it enters the tube is `:`
View SolutionA particle of mass `0.1kg` is launched at an angle of `53^(@)` with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than `12.5m` and which is inclined at an angle of `37^(@)` with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is `mu=(3)/(8)[` Take `g=10m//g^(2)]`

The kinetic energy of the particle when it comes out of the tube is approximately equal to `:`
View SolutionA particle of mass `0.1kg` is launched at an angle of `53^(@)` with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than `12.5m` and which is inclined at an angle of `37^(@)` with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is `mu=(3)/(8)[` Take `g=10m//g^(2)]`

The distance from the point of projection where the particle will land on the horizontal plane after coming out from the tube is approximately equal to `:`
View SolutionTwo bodies A and B of masses `10 kg` and `5 kg` placed very slightly seperated as shown in figure The coefficient of friction between the floor and the block are as `mu_(s) = 0.4` block A is pushed by an external force F The value of F can be changed when the weight between block A and ground breaks block A will start prssing block B will start pressing the vertical wall

If `F = 20N`,with how much force block A press block B?
View SolutionTwo bodies A and B of masses `10 kg and 5 kg` placed very slightly seperated as shown in figure The coefficient of friction between the floor and the block are as `mu_(s) = 0.4` block A is pushed by an external force F The value of F can be changed when the weight between block A and ground breaks block A will start pressing block B will start pressing the vertical wall

The force of friction acting on B verius with the applied force F acceleration to curve
View SolutionTwo bodies A and B of masses `10 kg and 5 kg` placed very slightly seperated as shown in figure The coefficient of friction between the floor and the block are as `mu_(s) = 0.4` block A is pushed by an external force F The value of F can be changed when the weight between block A and ground breaks block A will start prssing block B will start pressing the vertical wall

If `F = 50N `the friction force acting between block B and ground will be
View SolutionOne end of massless inextensible string of length `l` is fixed and other end is tied to a small ball of mass `m`. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is `sqrt(20gl)`. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is `g`.
Motion of ball is in nature of
View SolutionOne end of massless inextensible string of length `l` is fixed and other end is tied to a small ball of mass `m`. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is `sqrt(20gl)`. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is `g`.
At the highest position of ball, tangential acceleration of ball is `-`
View SolutionOne end of massless inextensible string of length `l` is fixed and other end is tied to a small ball of mass `m`. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is `sqrt(20gl)`. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is `g`.
During circular motion, minimum value of tension in the string`-`
View SolutionFigure shows an irregular wedge of mass `m` placed on a smooth horizontal surface. Part `BC` is rough.
What minimum velocity should be imparted to a small block of same mass `m` so that it may each point `B` :
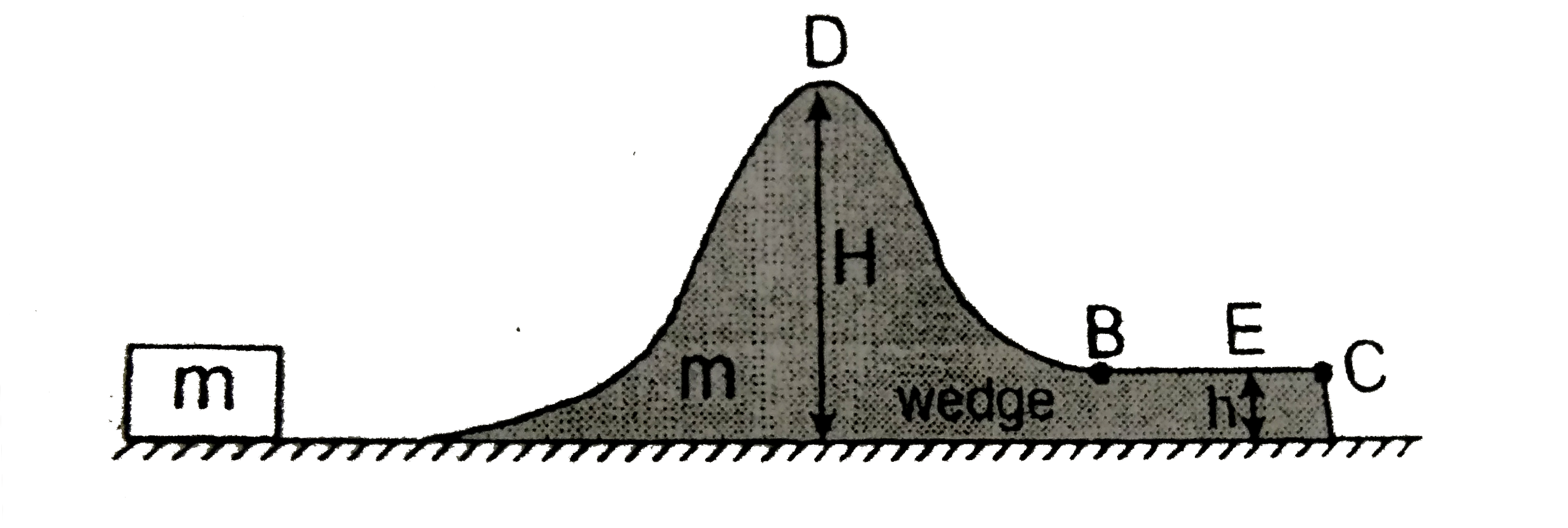
View SolutionFigure shows an irregular wedge of mass `m` placed on a smooth horizontal surface. Part `BC` is rough.
What minimum velocity should be imparted to a small block of same mass `m` so that it may each point `B` :

View SolutionFigure shows an irregular wedge of mass `m` placed on a smooth horizontal surface. Part `BC` is rough.
What minimum velocity should be imparted to a small block of same mass `m` so that it may each point `B` :

View SolutionAn initially stationary box on a frictionless floor explodes into two pieces, piece `A` with mass `m_(A)` and piece `B` with mass `m_(B)`. Two pieces then move across the floor along `x-` axis. Graph of position versus time for the two pieces are given.
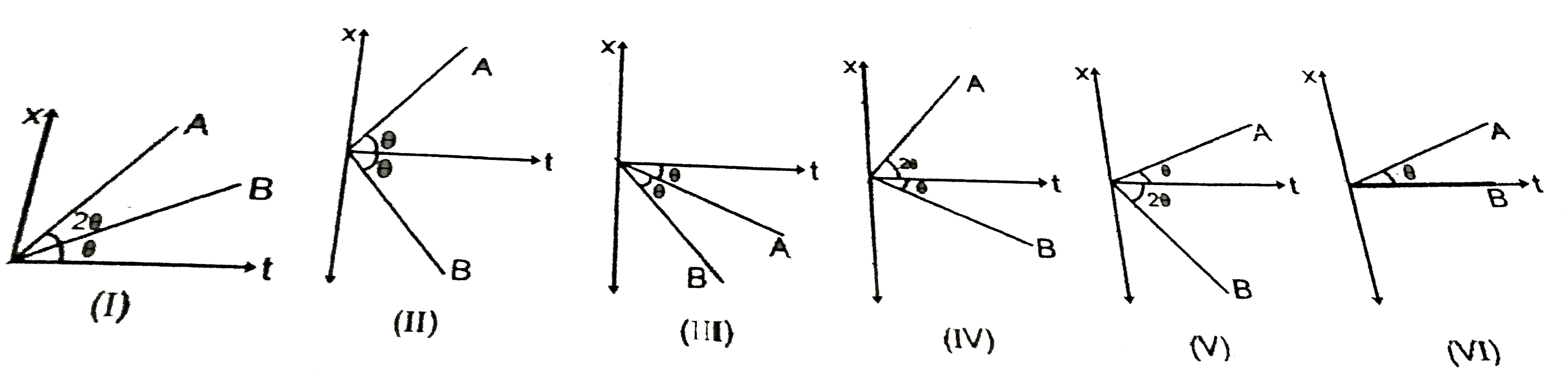
Which graphs pertain to physically possible explosions ?
View SolutionAn initially stationary box on a frictionless floor explodes into two pieces, piece `A` with mass `m_(A)` and piece `B` with mass `m_(B)`. Two pieces then move across the floor along `x`-axis. Graph of position versus time for the two pieces are given

Which graphs pertain to physically possible explosion?
View SolutionTwo racing cars `'A'` and `'B'` having masses `'M'` and `'2m'` respectively start running from the starting line on a horizontal plane.Both cars `'A'` and `B'` have same speed `'V'` which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres `O_(1)` and `O_(2)` as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
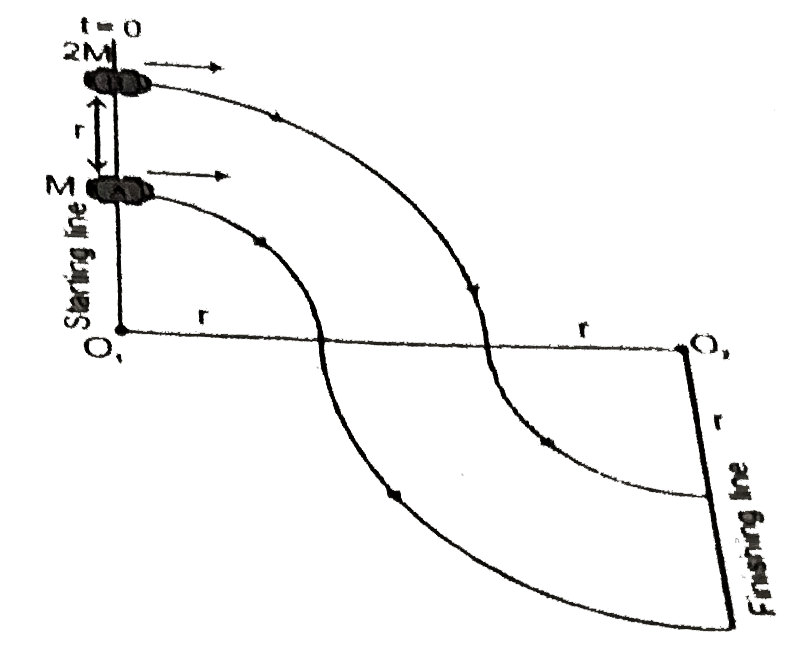
Graph between the magnitude of relative velocity of the two car and time is `:`
View SolutionTwo racing cars `'A'` and `'B'` having masses `'M'` and `'2m'` respectively start running from the starting line on a horizontal plane.Both cars `'A'` and `B'` have same speed `'V'` which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres `O_(1)` and `O_(2)` as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

The magnitude of relative acceleration of two cars when car `'A'` just reaches the end of circular arc of radius `Y`.
View SolutionTwo racing cars `'A'` and `'B'` having masses `'M'` and `'2m'` respectively start running from the starting line on a horizontal plane.Both cars `'A'` and `B'` have same speed `'V'` which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres `O_(1)` and `O_(2)` as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
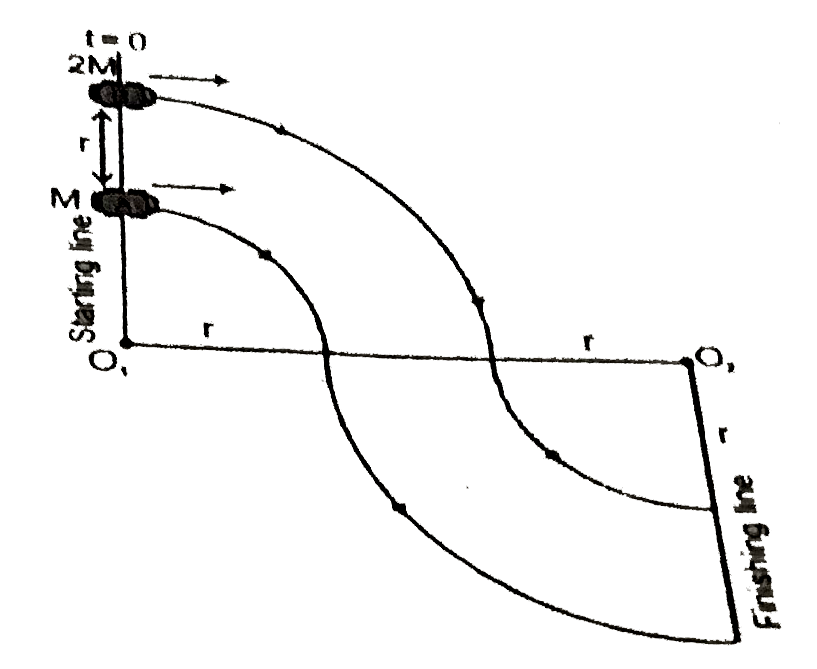
The time interval during which the two cars have same angular speed `:`
View SolutionTwo racing cars `'A'` and `'B'` having masses `'M'` and `'2m'` respectively start running from the starting line on a horizontal plane.Both cars `'A'` and `B'` have same speed `'V'` which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres `O_(1)` and `O_(2)` as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

Which of the following statements is incorrect.
View SolutionTwo beads of mass `2m` and `m`, connected by a rod of length `l` and of negligible mass are free to move in a smooth vertical circular wire frame of radius `l` as shown. Initially the system is held in horizontal position `(` Refer figure `)`

If the rod is replaced by a massless string of length `l` and the system is released when the string is horizontal then `:`
View SolutionTwo beads of mass `2m` and `m`, connected by a rod of length `l` and of negligible mass are free to move in a smooth vertical circular wire frame of radius `l` as shown. Initially the system is held in horizontal position `(` Refer figure `)`

If the rod is replaced by a massless string of length `l` and the system is released when the string is horizontal then `:`
View SolutionTwo beads of mass `2m` and `m`, connected by a rod of length `l` and of negligible mass are free to move in a smooth vertical circular wire frame of radius `l` as shown. Initially the system is held in horizontal position `(` Refer figure `)`

If the rod is replaced by a massless string of length `l` and the system is released when the string is horizontal then `:`
View SolutionA ball is projected on a very long floor. There may be two conditions `(i)` floor is smooth `& (ii)` the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed `u` at an angle `30^(@)` with horizontal and it is known that after collision with the floor its speed becomes `(u)/(sqrt(3))` . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is `:`
View SolutionA ball is projected on a very long floor. There may be two conditions `(i)` floor is smooth `& (ii)` the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.
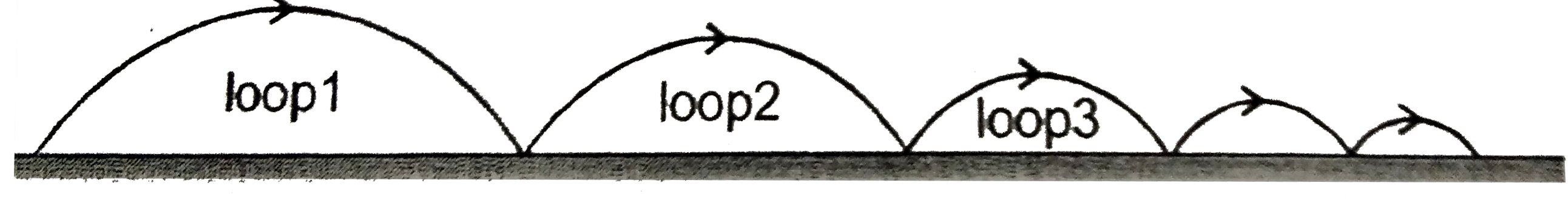
Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed `u` at an angle `30^(@)` with horizontal and it is known that after collision with the floor its speed becomes `(u)/(sqrt(3))` . Then answer the following questions.
The ratio of maximum height reached by ball in first loop and second loop `((H_(1))/(H_(2)))` is `:`
View SolutionA ball is projected on a very long floor. There may be two conditions `(i)` floor is smooth `& (ii)` the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed `u` at an angle `30^(@)` with horizontal and it is known that after collision with the floor its speed becomes `(u)/(sqrt(3))` . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been `:`
View SolutionA smooth rope of mas `m` and length `L` lies in a heap on a smooth horizontal floor, with one end attached to a block of mass `M`. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude `V_(0)` as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance `x` from point `P` as shown in figure `-2( P` is a point on the rope which has just started to move at the given instant `)`, choose correct options for next three question.

The speed of block of mass `M` is
View SolutionA smooth rope of mas `m` and length `L` lies in a heap on a smooth horizontal floor, with one end attached to a block of mass `M`. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude `V_(0)` as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance `x` from point `P` as shown in figure `-2( P` is a point on the rope which has just started to move at the given instant `)`, choose correct options for next three question.

The speed of block of mass `M` is
View SolutionA smooth rope of mas `m` and length `L` lies in a heap on a smooth horizontal floor, with one end attached to a block of mass `M`. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude `V_(0)` as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance `x` from point `P` as shown in figure `-2( P` is a point on the rope which has just started to move at the given instant `)`, choose correct options for next three question.

The speed of block of mass `M` is
View SolutionUniform rod `AB` is hinged at the end `A` in a horizontal position as shown in the figure `(` the hinge is frictionless that is , it does not exert any friction force on the rod `)`. The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to `'m'`.
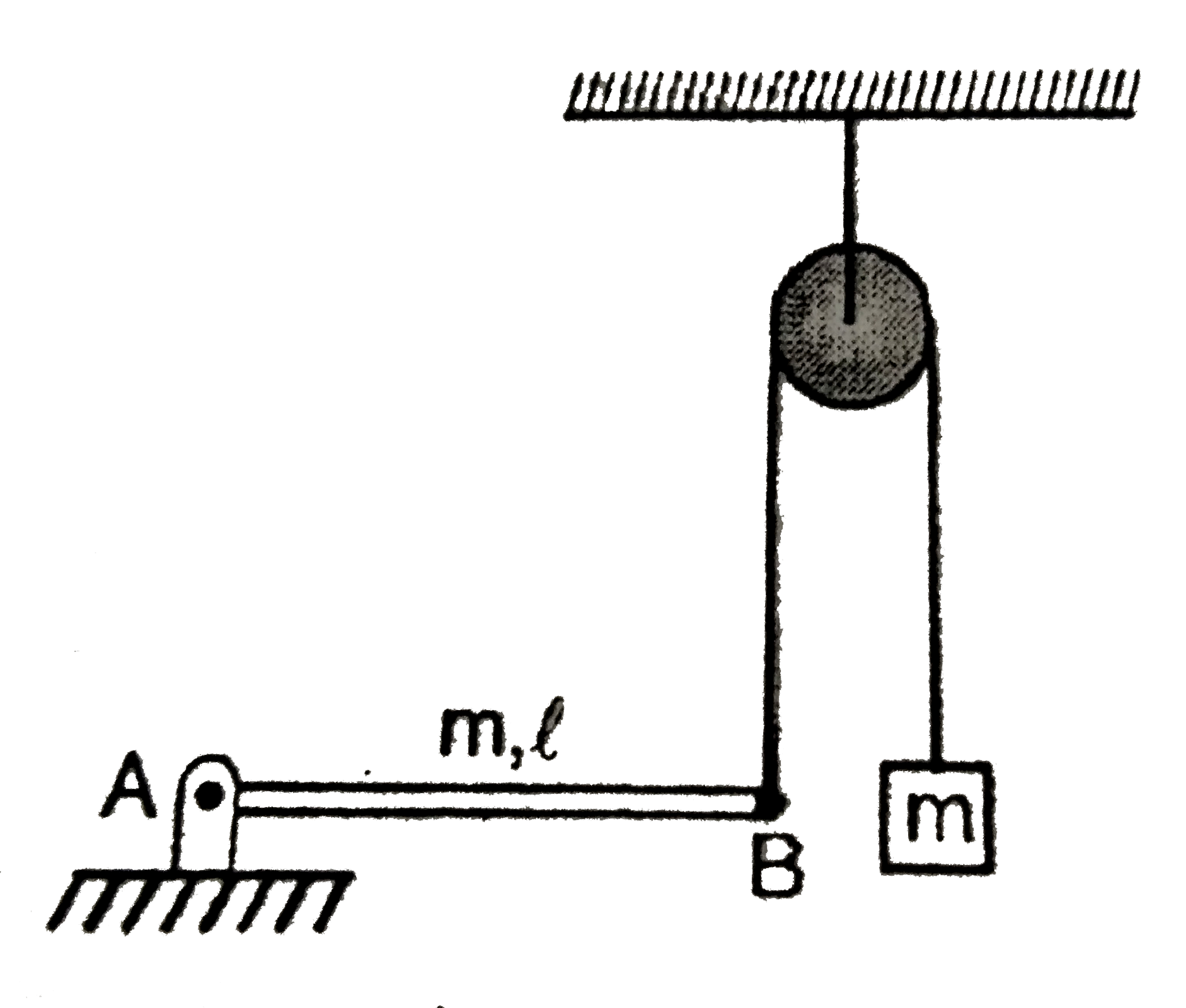
Then just after release of block from this position, the tension in the thread is
View SolutionUniform rod `AB` is hinged at the end `A` in a horizontal position as shown in the figure `(` the hinge is frictionless that is , it does not exert any friction force on the rod `)`. The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to `'m'`.
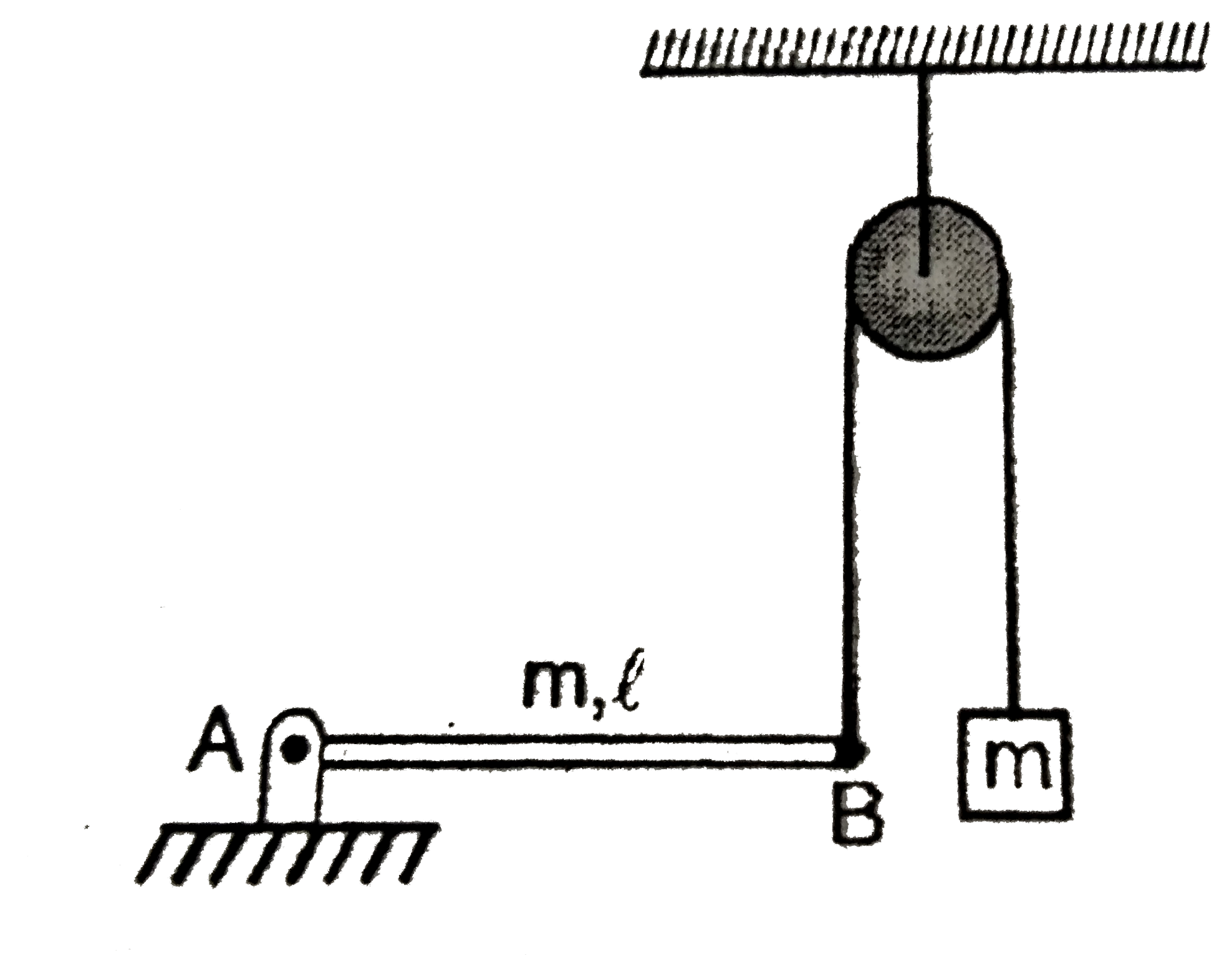
Then just after released of block from this position, the angular acceleration of the rod is
View SolutionUniform rod `AB` is hinged at the end `A` in a horizontal position as shown in the figure `(` the hinge is frictionless that is , it does not exert any friction force on the rod `)`. The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to `'m'`.

Then just after release of block from this position, the magnitude of reaction exerted by hinge on the rod is
View SolutionA smooth ball `'A'` moving with velocity `'V'` collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities `60^(@)`. No external force acts on the system of balls.

The speed of each ball after the collision is
View SolutionA smooth ball `'A'` moving with velocity `'V'` collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities `60^(@)`. No external force acts on the system of balls.

If the kinetic energy lost is fully converted to heat then heat produced is
View SolutionA smooth ball `'A'` moving with velocity `'V'` collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities `60^(@)`. No external force acts on the system of balls.

The value of coefficient of resititution is
View SolutionA horizontal uniform rod of mass `'m'` has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass `'m'` which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
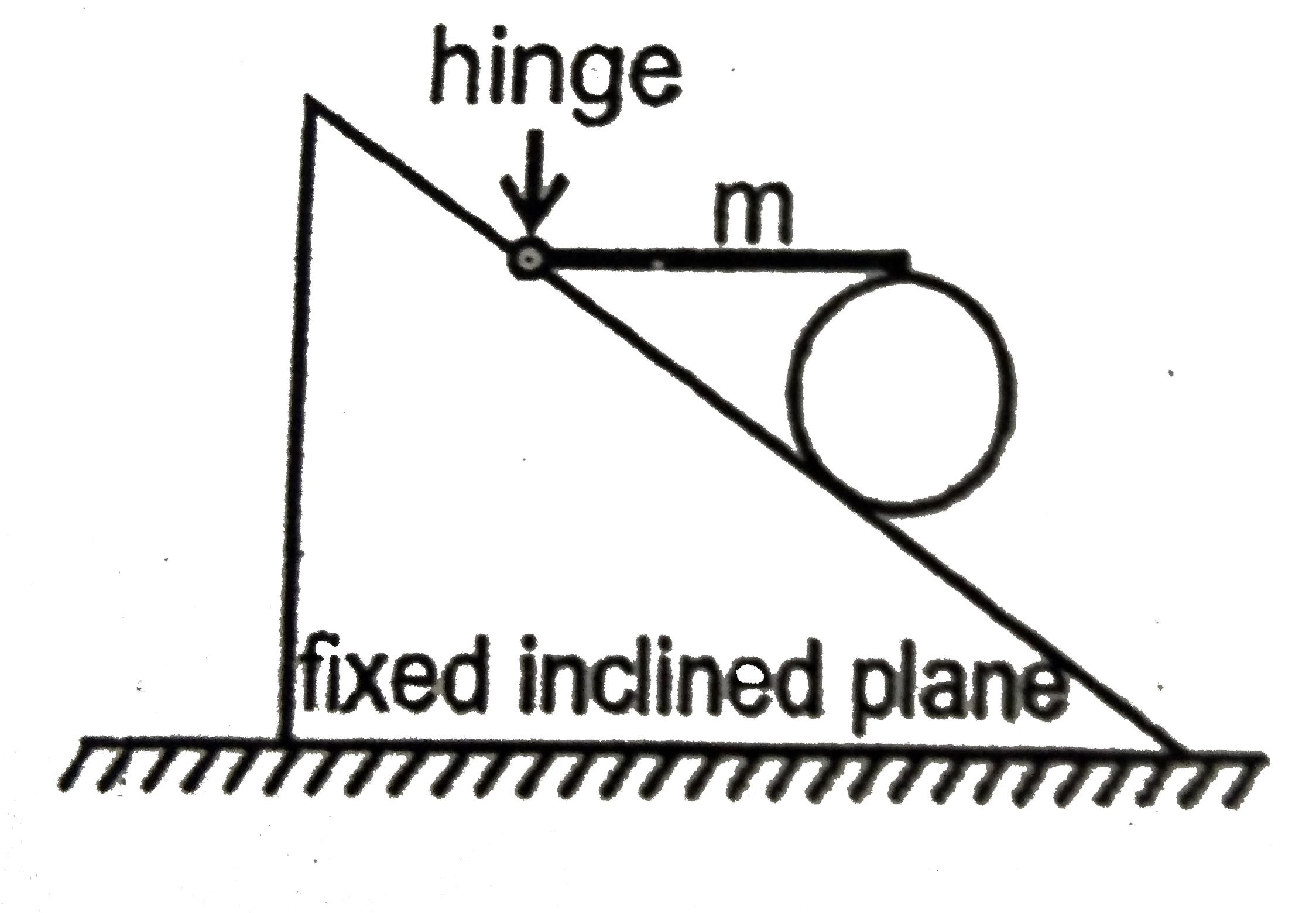
The magnitude of normal reaction exerted by the rod on the cylinder is
View SolutionA horizontal uniform rod of mass `'m'` has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass `'m'` which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
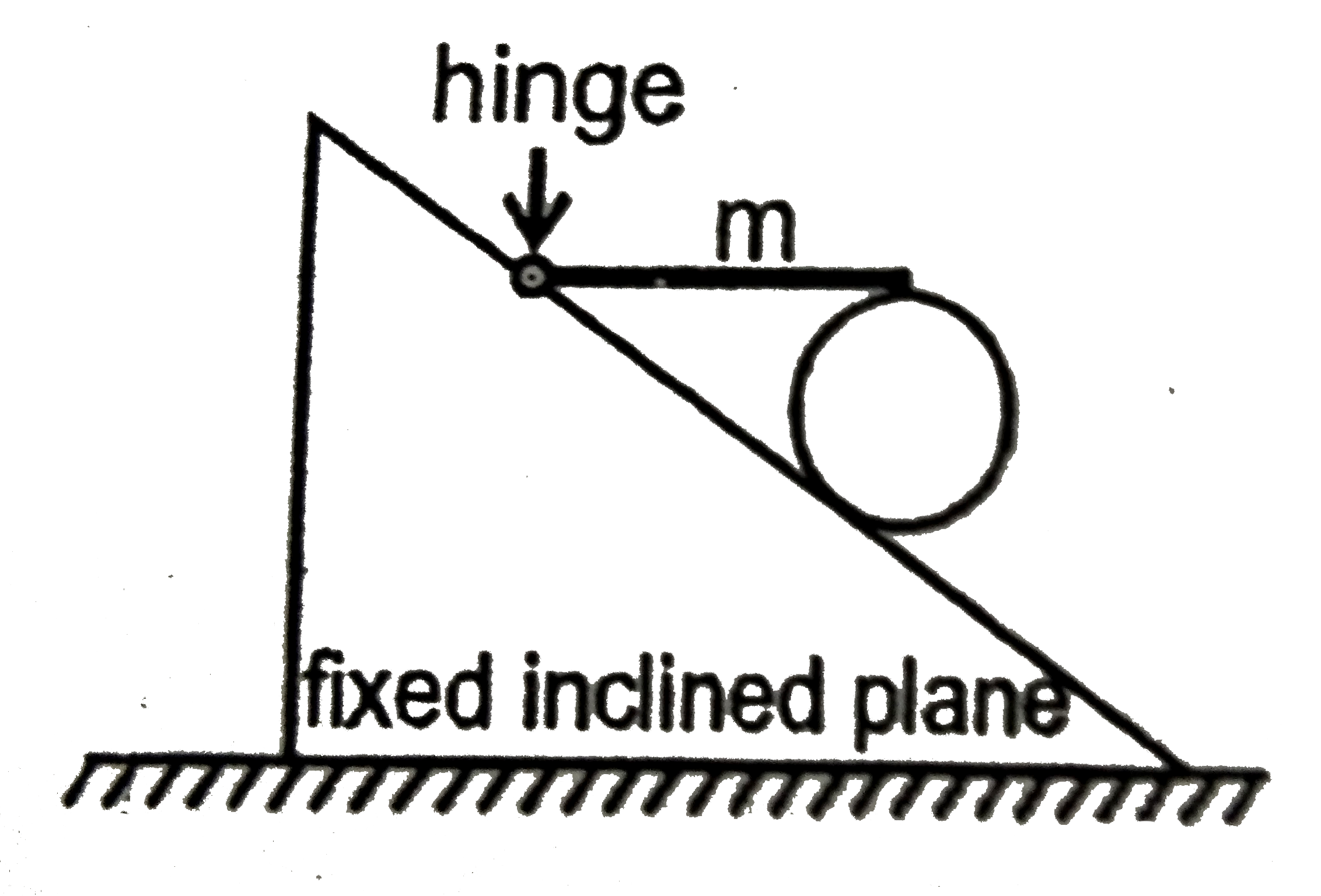
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is `:`
View SolutionA horizontal uniform rod of mass `'m'` has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass `'m'` which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The magnitude of normal reaction exerted by the inclinded plane on the cylinder is `:`
View SolutionA small ball `(` uniform solid sphere `)` of mass `m` is released from the top of a wedge of the same mass `m`. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.
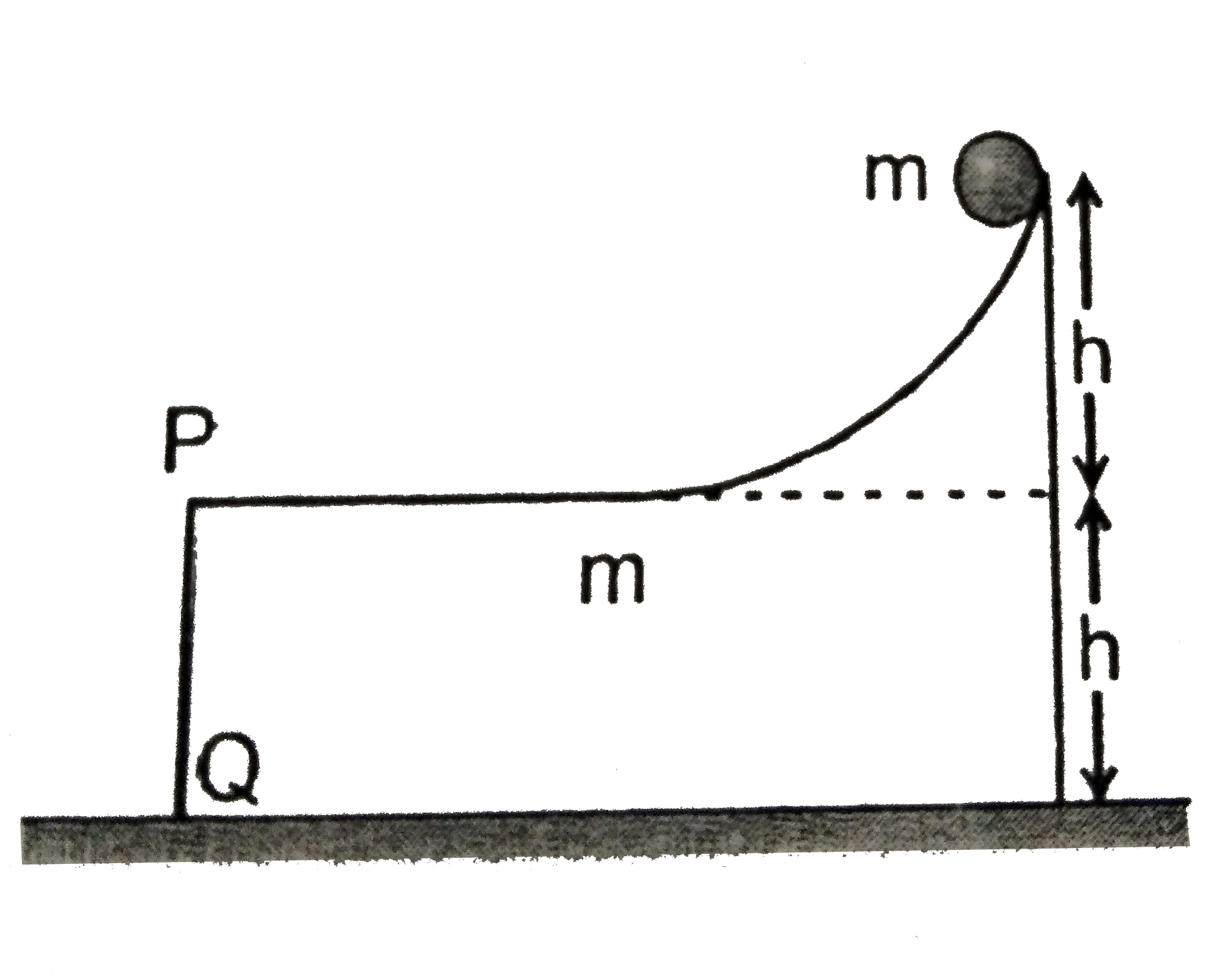
The speed of the wedge when the ball is just going to leave the wedge at point `'P'` of the wedge is
View SolutionA small ball `(` uniform solid sphere `)` of mass `m` is released from the top of a wedge of the same mass `m`. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.
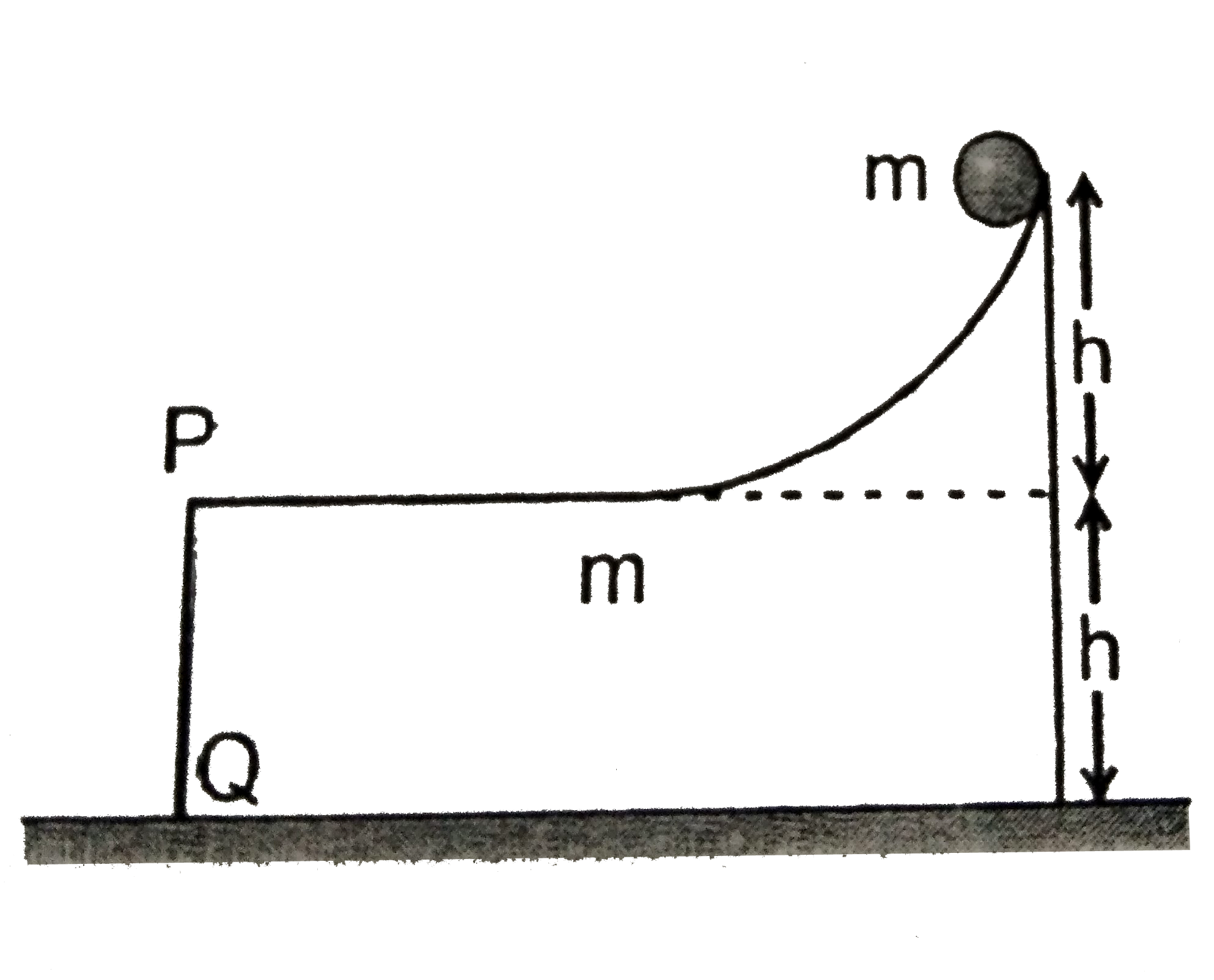
The total kinetic energy of the ball just before it falls on the ground
View SolutionA small ball `(` uniform solid sphere `)` of mass `m` is released from the top of a wedge of the same mass `m`. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.

The horizontal separation between the ball and the edge `'PQ'` of wedge just before the ball falls on the groun is
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity `v_(0)` and angular velocity` omega_(0)` as shown in the figure below. Point `O` is the centre of mass of the wheel and point `P` is its instantaneous point of contact with the groundl. The radius of wheel is `r` and its radius of gyration about `O` is `k`. Coefficient of friction between wheel and ground is `mu`. A is a fixed point on the ground.
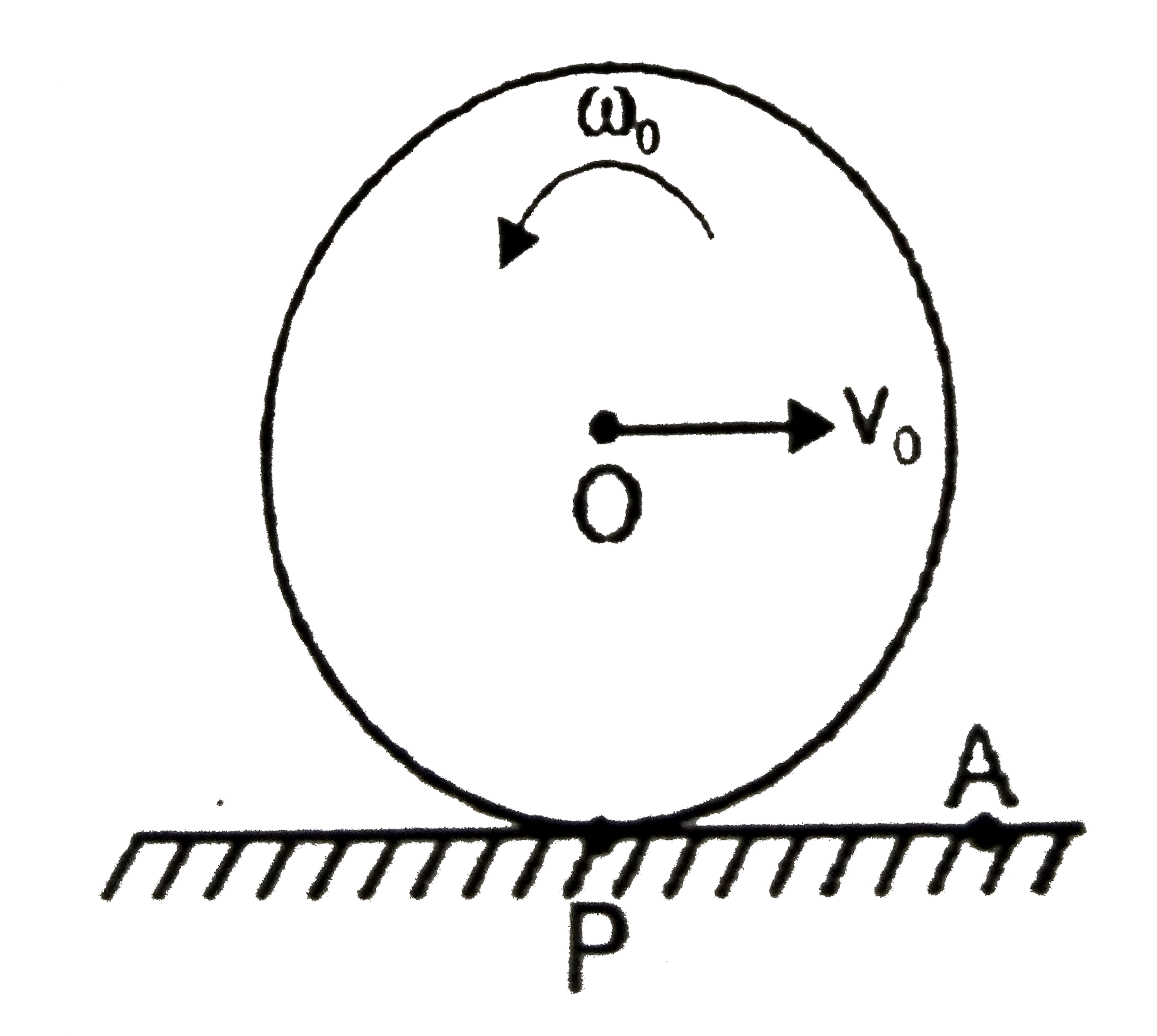
Which of the following is conserved ?
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity `v_(0)` and angular velocity` omega_(0)` as shown in the figure below. Point `O` is the centre of mass of the wheel and point `P` is its instantaneous point of contact with the groundl. The radius of wheel is `r` and its radius of gyration about `O` is `k`. Coefficient of friction between wheel and ground is `mu`. A is a fixed point on the ground.
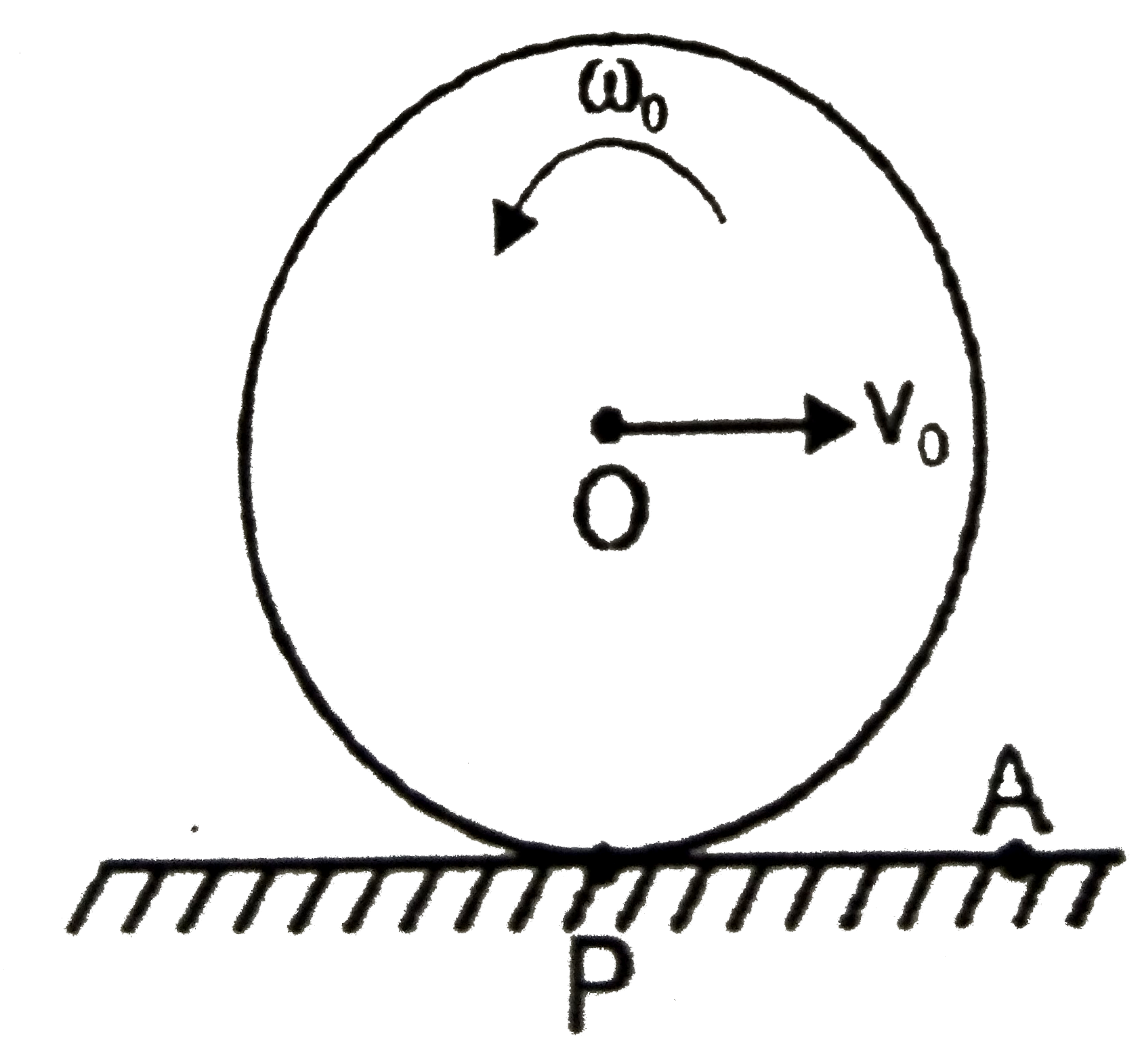
If the wheel comes to permanent rest after sometimes, then `:`
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity `v_(0)` and angular velocity` omega_(0)` as shown in the figure below. Point `O` is the centre of mass of the wheel and point `P` is its instantaneous point of contact with the groundl. The radius of wheel is `r` and its radius of gyration about `O` is `k`. Coefficient of friction between wheel and ground is `mu`. A is a fixed point on the ground.
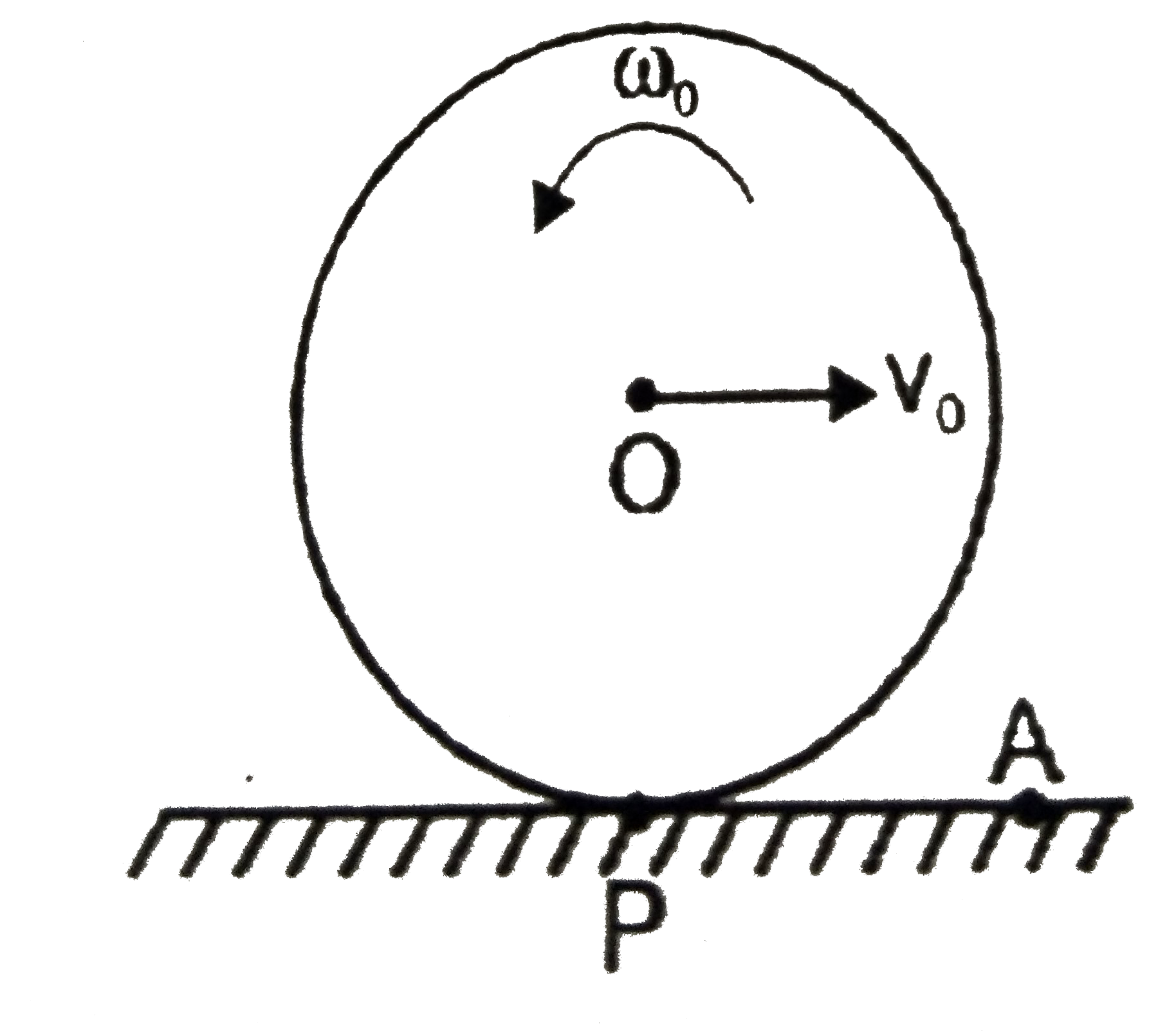
If above question , distance travelled by centre of mass of the wheel before it stops is `-`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.
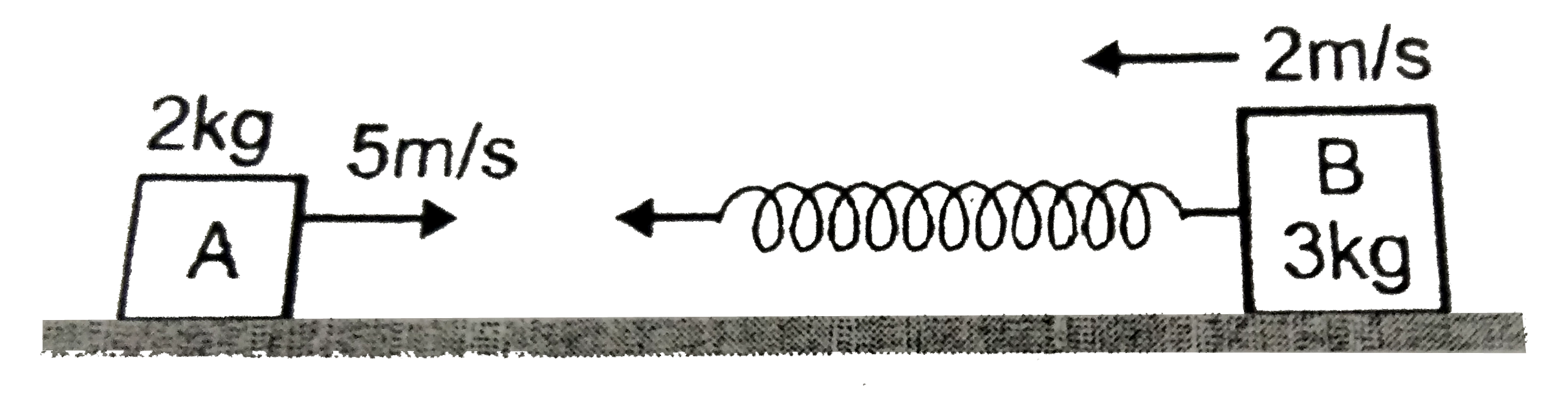
Velocity of centre of mass of the system of blocks `A` and `B`, before collision is `:`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.
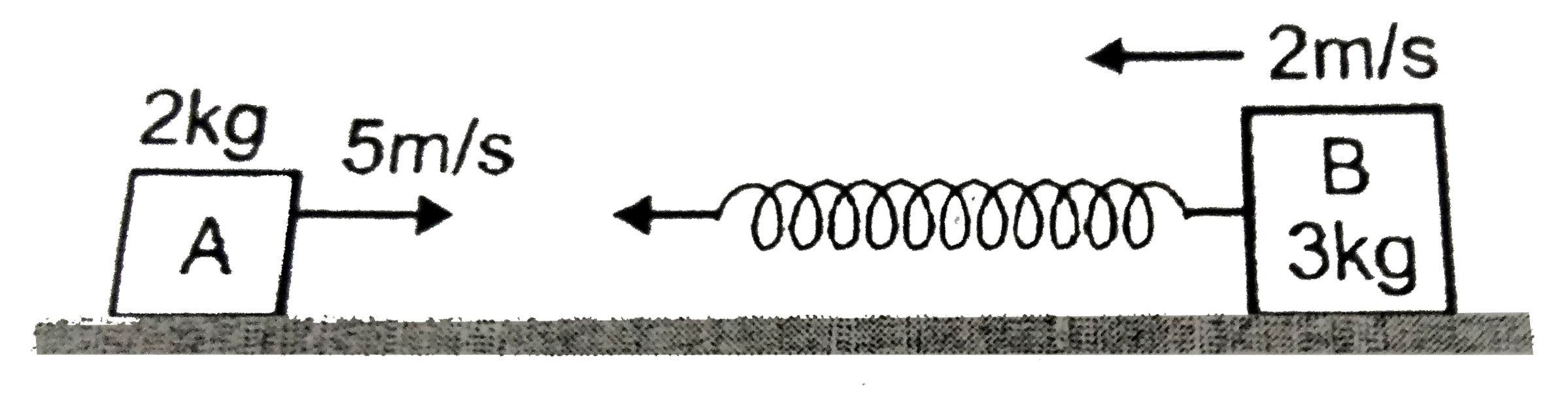
In the collision process, while the spring is getting compressed `:`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.

In the collision process, while the spring is getting compressed `:`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.

In the collision process, while the spring is getting compressed `:`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.
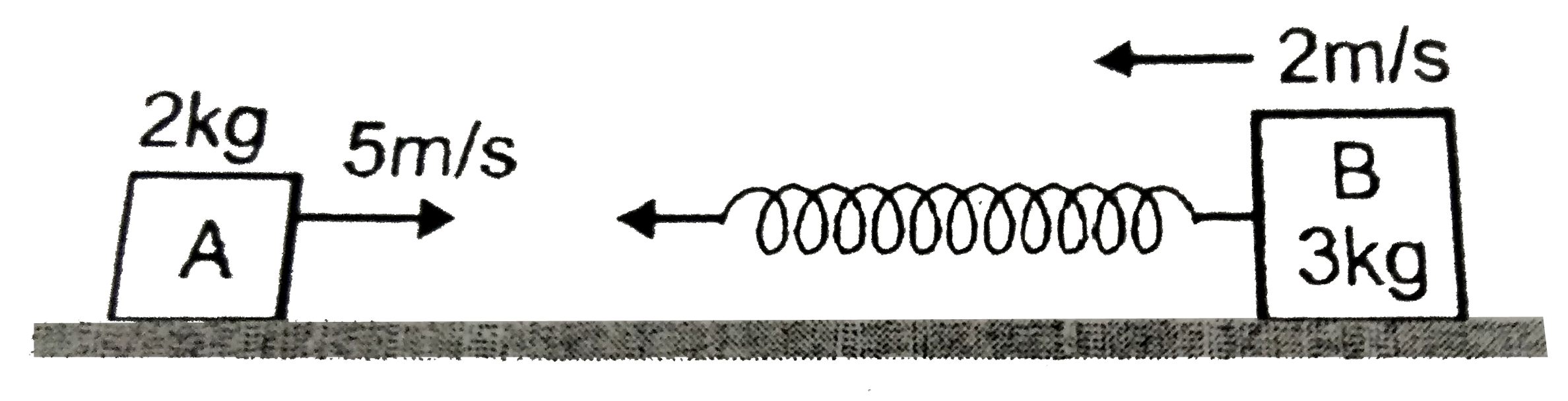
When the blocks are yet to attain their final velocities, in this situation at any instant when block `A` is moving with a velocity `4 hat(i) m//s` , velocity of block `B` will then be `:`
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
View SolutionIn figure, a block `A` of mass `2kg` is moving to the right with a speed `5m//s` on a horizontal frictionless surface. Another block `B` of mass `3kg` a massless spring of spring constant `222N//m` attached to it, is moving to the left on the same surface and with a speed `2m//s` . Let us take the direction to the right as the positive `X-` direction. At some instant, block `A` collides with the spring attached to block `B`. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that `(i)` the spring force is conservative and so there is no conversion of kinetic energy to internal energy and `(ii)`, no sound is made when block `A` hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
View SolutionA smooth horizontal fixed pipe is bent in the form of a vertical circle of radius `20m` as shown in figure. A small glass ball is shown in horizontal portion of pipe at speed `30m//s` as shown from end `A`. `(` Take `g=10m//s^(2))`
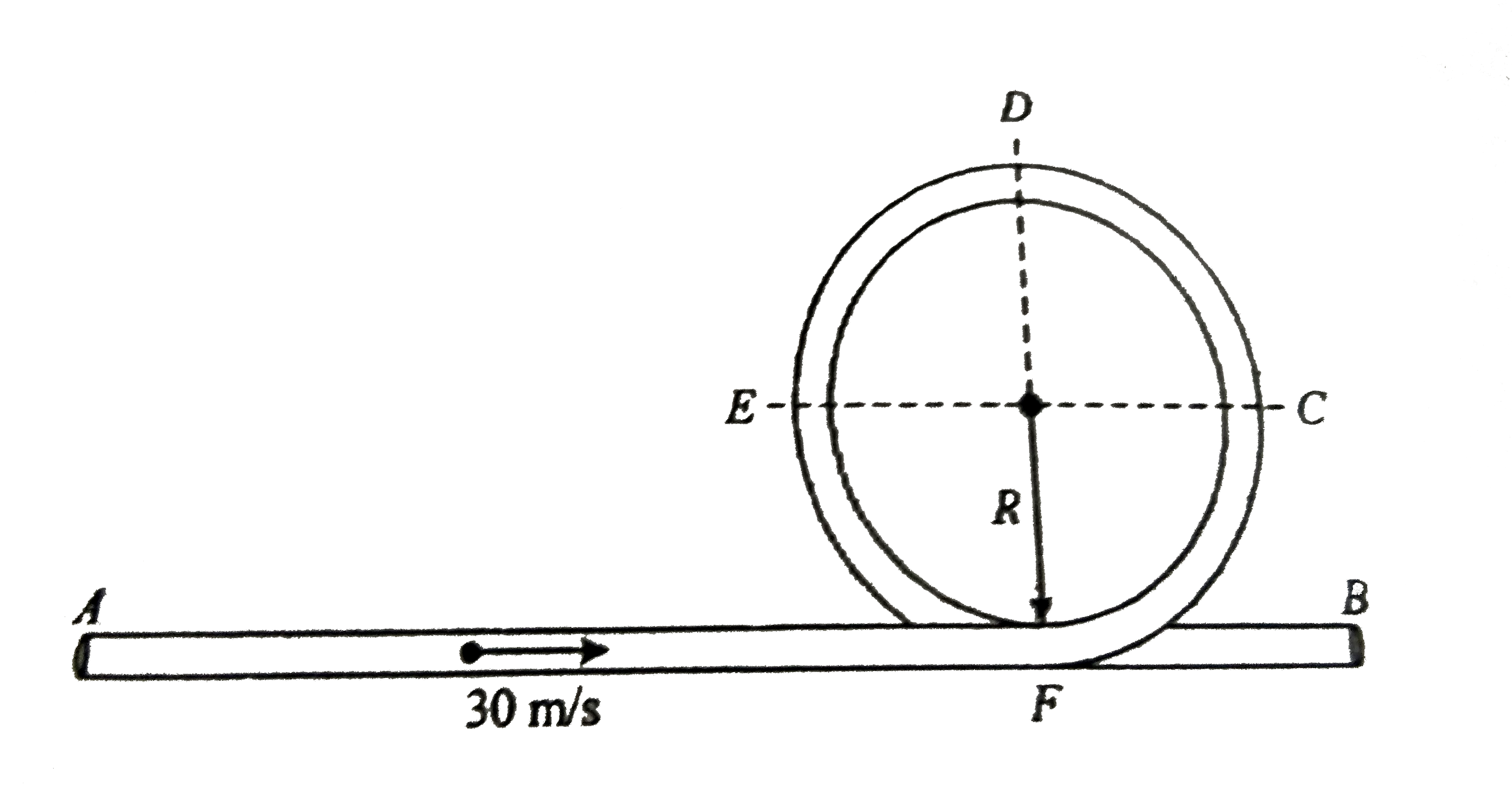
Which of the following statement is `//` are correct `:`
`(i)` ball will not come out from eend `B`.
`(ii)` ball will come out from end `B`.
`(iii)` At point `D` speed of ball will be just more than zero.
`(iv)` At point `E` and `C` the ball will have same speed.
View SolutionA smooth horizontal fixed pipe is bent in the form of a vertical circle of radius `20m` as shown in figure. A small glass ball is shown in horizontal portion of pipe at speed `30m//s` as shown from end `A`. `(` Take `g=10m//s^(2))`
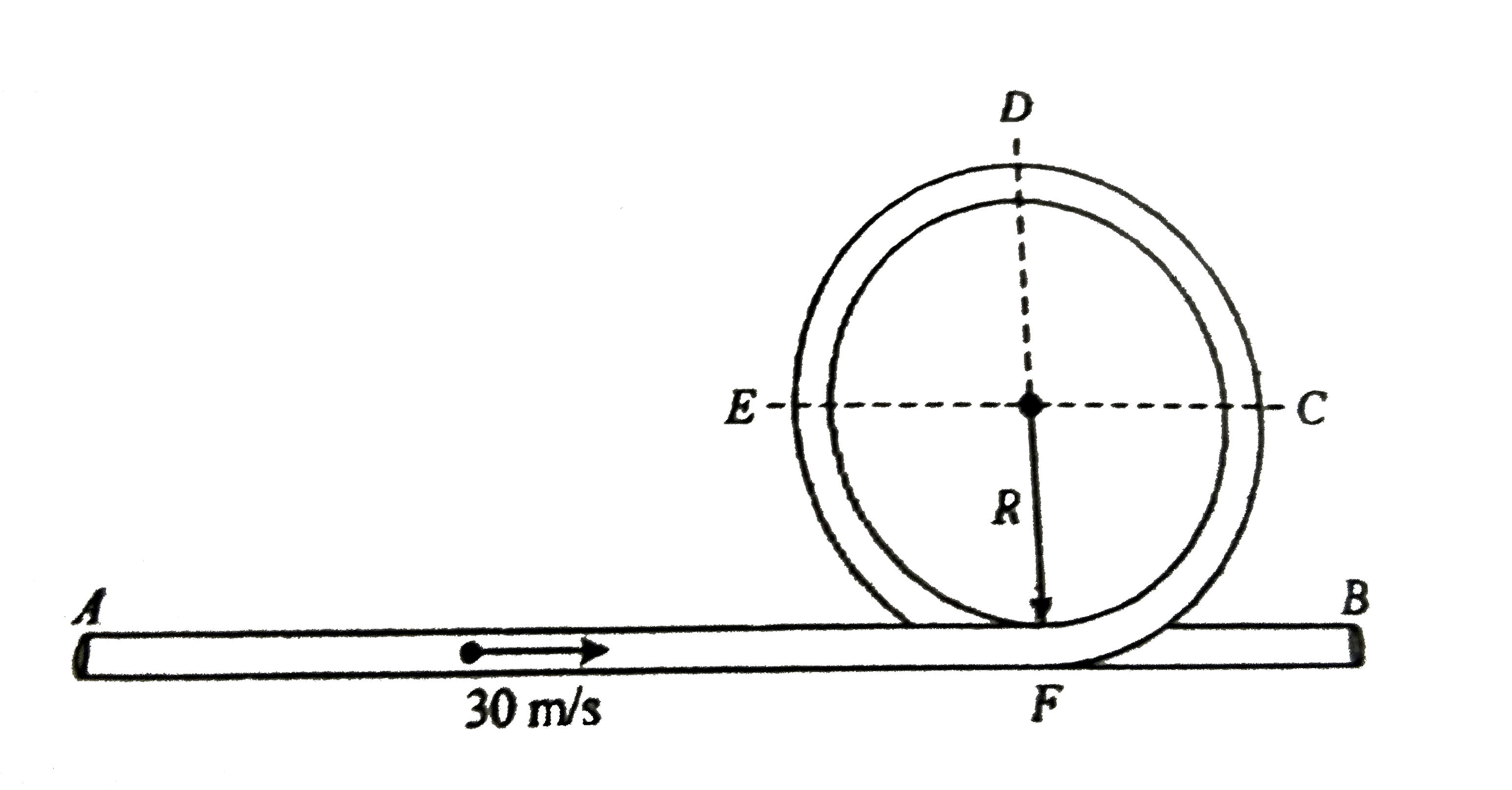
At which angle from vertical from bottom most point `F`. The normal reaction on ball due to pipe will change its direction `(` in terms of radially outwards and inwards `) :`
View SolutionA smooth horizontal fixed pipe is bent in the form of a vertical circle of radius `20m` as shown in figure. A small glass ball is shown in horizontal portion of pipe at speed `30m//s` as shown from end `A`. `(` Take `g=10m//s^(2))`
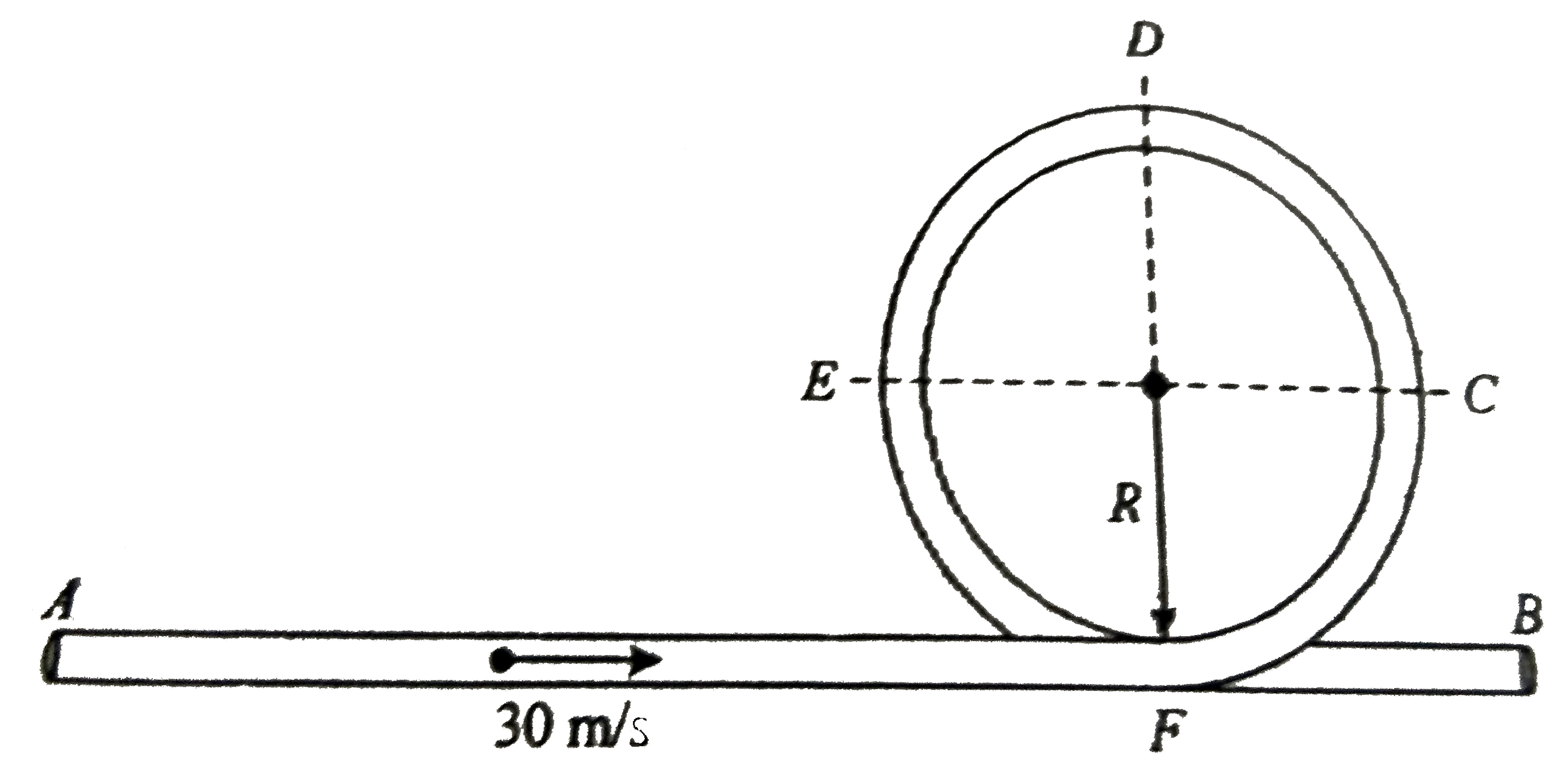
With what speed ball willcome out from point `B :`
View SolutionA block of mass `m` slides down a wedge of mass `M` as shown . The whole system is at rest , when the height of the block is `h` above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
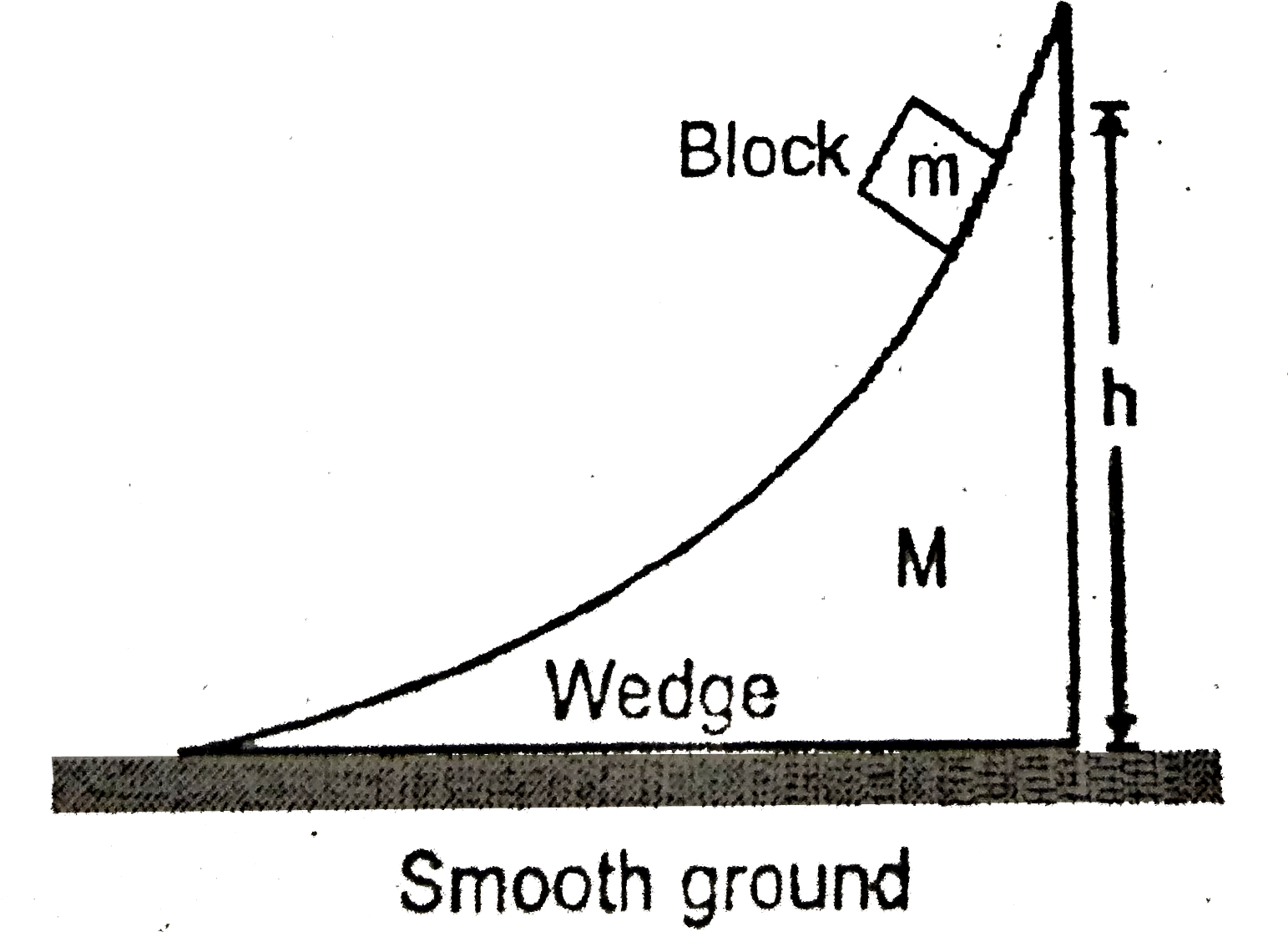
As the block slides down, which of the following quantities associated with the system remains conserved ?
View SolutionA block of mass `m` slides down a wedge of mass `M` as shown . The whole system is at rest , when the height of the block is `h` above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
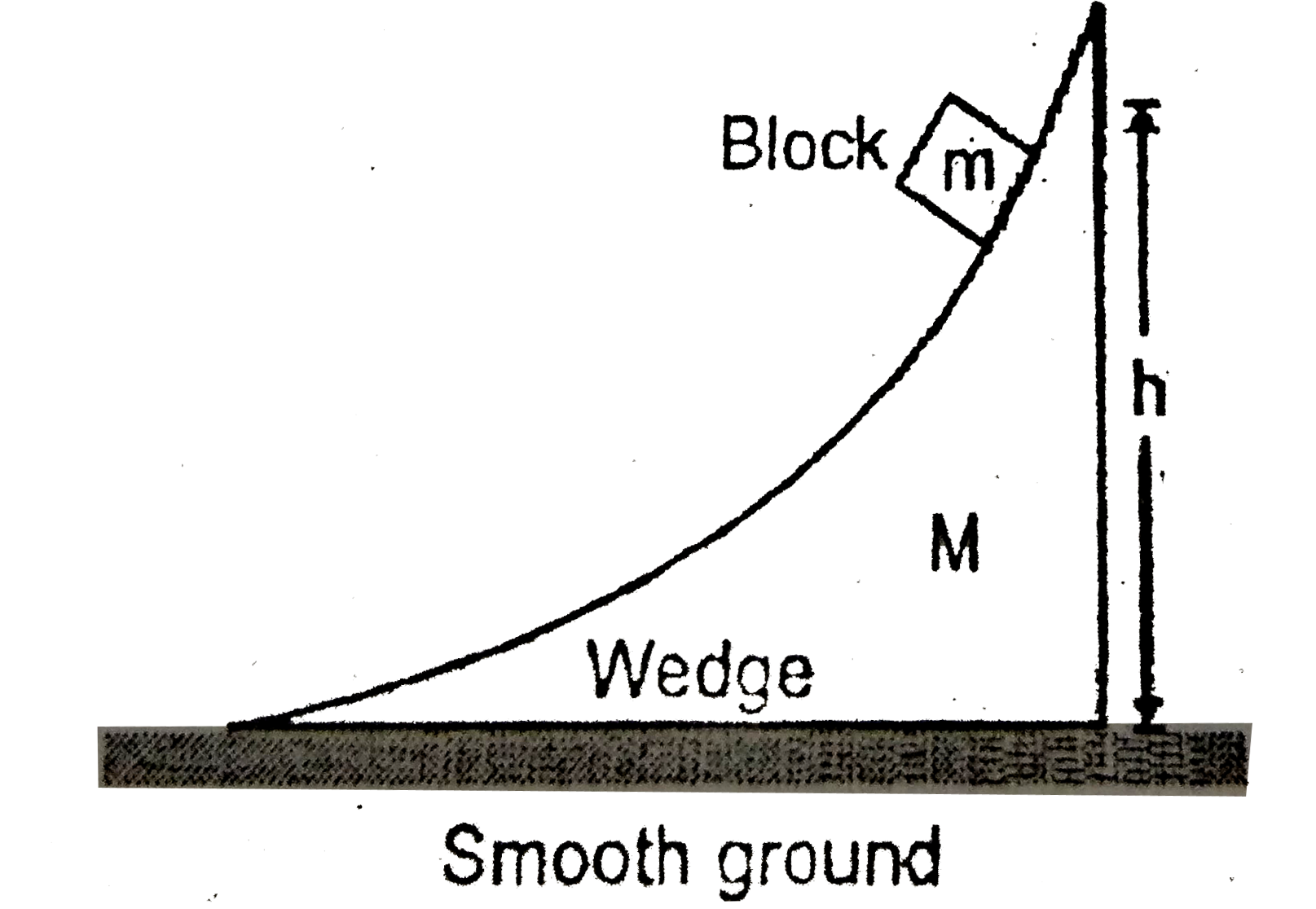
If there would have been friction wedge and block , which of the following quantities would still remains conserved ?
View SolutionA block of mass `m` slides down a wedge of mass `M` as shown . The whole system is at rest , when the height of the block is `h` above the ground. The wedge surface is smooth and gradually flattens. There is no friction between wedge and ground.
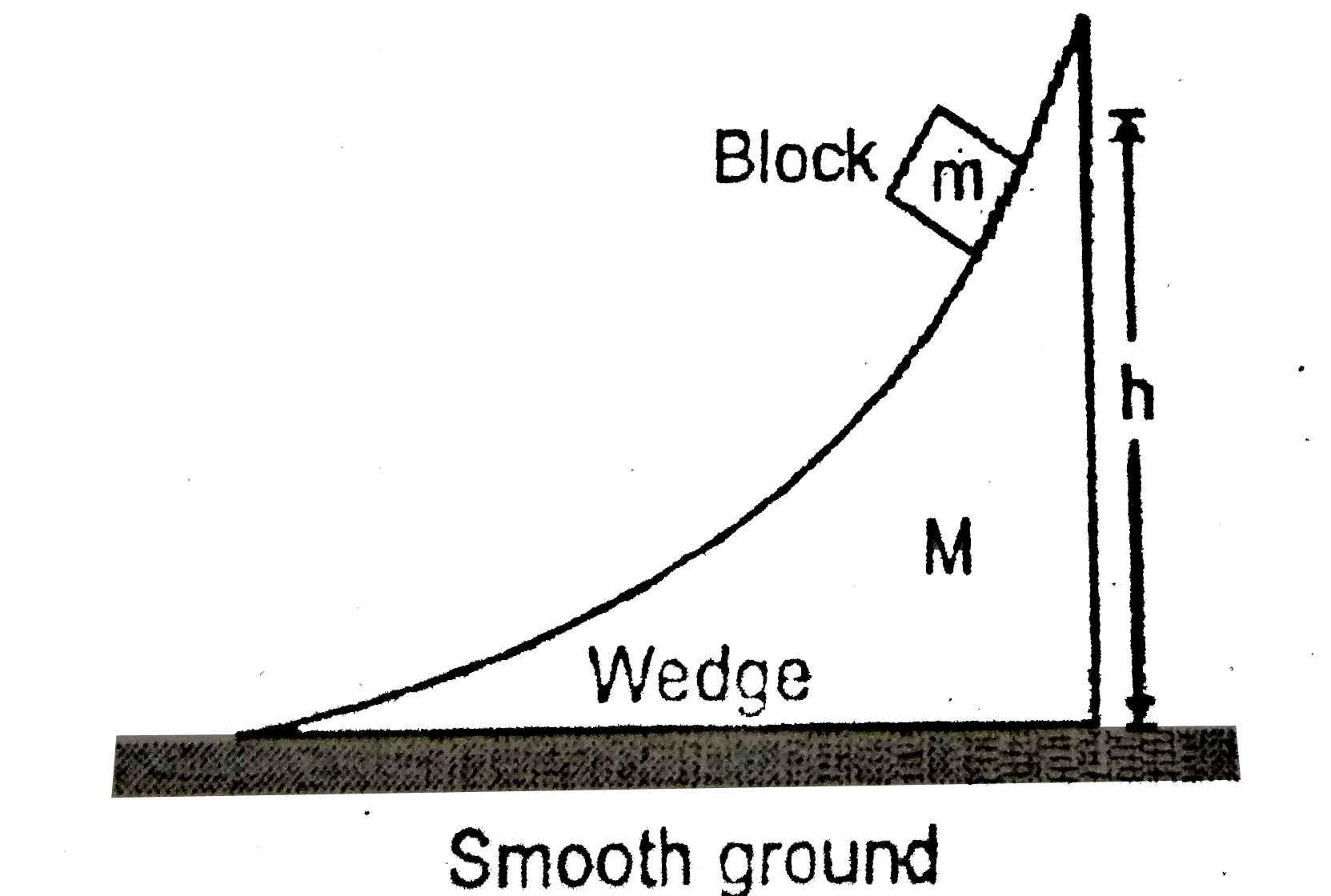
If there is no friction any where, the speed of the wedge, as the block leaves the wedge is `:`
View Solution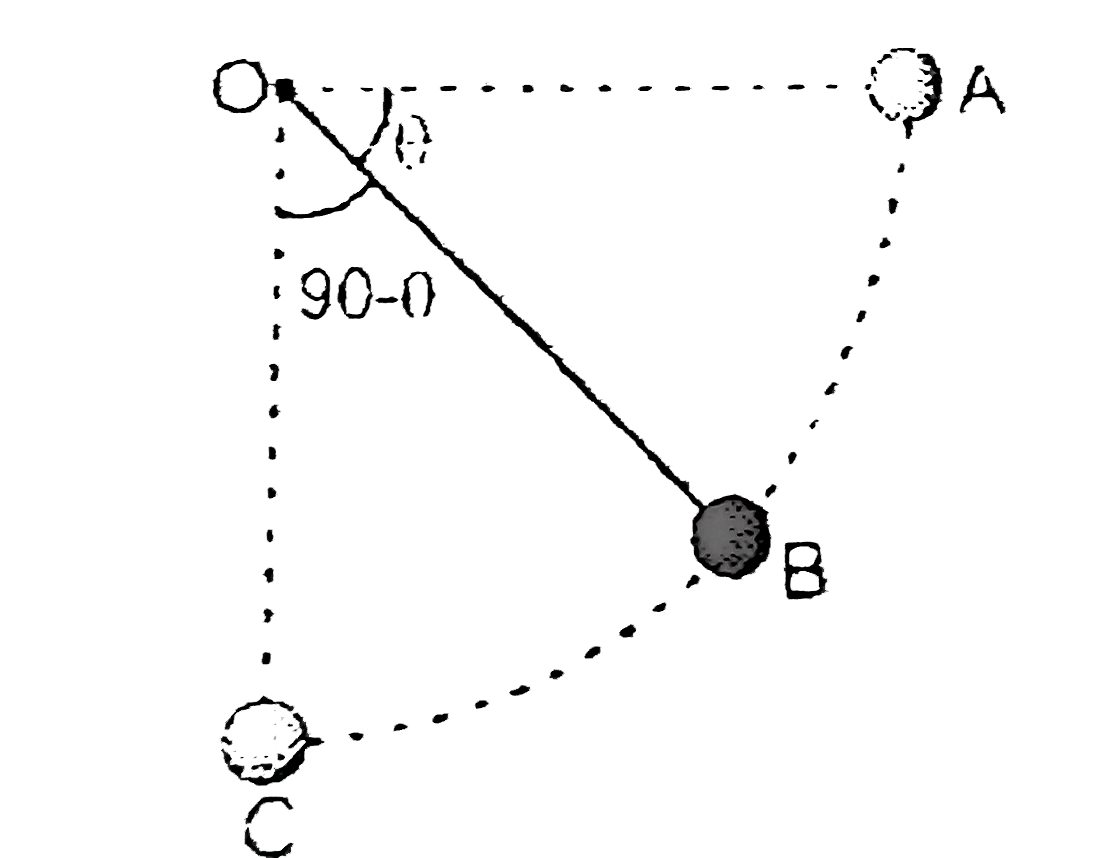
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. the ball is released from rest at `t=0` with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is `t_(1)` and from B to lowest position C is `t_(2)` let the velocity of ball at B is `vecv_(B)` and at C is `vecv_(C)` respectively.
Q. If `|vecv_(C)|=2|vecv_(B)|` then the value of `theta `as shown is
View Solution
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. the ball is released from rest at `t=0` with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is `t_(1)` and from B to lowest position C is `t_(2)` let the velocity of ball at B is `vecv_(B)` and at C is `vecv_(C)` respectively.
Q. If `|vecv_(C)|=2|vecv_(B)|` then the value of `theta `as shown is
View Solution
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. the ball is released from rest at `t=0` with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is `t_(1)` and from B to lowest position C is `t_(2)` let the velocity of ball at B is `vecv_(B)` and at C is `vecv_(C)` respectively.
Q. If `|vecv_(C)|=2|vecv_(B)|` then the value of `theta `as shown is
View Solution
comprehension questions and complete solutions for chapter DAILY PRACTICE PROBLEMS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS DAILY PRACTICE PROBLEMS
- comprehension
- Compreshension
- dpp 15
- dpp 16 physics
- dpp 17
- dpp 18
- dpp 19
- dpp 2 PHYSICS
- dpp 20
- dpp 21
- dpp 22.
- dpp 24
- dpp 25
- dpp 26
- dpp 27
- dpp 28
- dpp 30
- dpp 31
- dpp 32
- dpp 33
- dpp 34
- DPP 35
- dpp 36
- Dpp 37
- dpp 38
- dpp 39
- dpp 40
- dpp 41
- dpp 42
- dpp 43
- dpp 44
- DPP 45
- dpp 46
- dpp 47
- dpp 48
- dpp 49
- DPP 50
- dpp 51
- dpp 52
- dpp 53
- dpp 54
- DPP 55
- dpp 56
- dpp 57
- dpp 58
- dpp 59
- dpp 60
- DPP 62
- dpp 63
- dpp 64
- DPP 65
- dpp 66
- dpp 67
- dpp 68
- dpp 69
- dpp 70
- dpp 71
- dpp 72
- dpp 74
- dpp 75
- dpp 76
- DPP 77
- dpp 78
- dpp 79
- DPP 8 PHYSICS
- dpp 80
- dpp 81
- dpp 82
- dpp 83
- dpp 84
- dpp 85
- dpp 86
- dpp 87
- dpp 88
- dpp 89 illustration
- dpp 90 Illustration
- dpp 91 illustration
- dpp 92 illustration
- Dpp no 10 physics
- Dpp no 11 physics
- Dpp no 12 Physics
- Dpp no 6 physics
- DPP NO 7 PHYSICS
- DPP no 9 physics
- Dpp no. 13 physics
- DPP NO. 14 PHYSICS
- DPP NO. 5 Physics
- dpp23
- dpp29
- dpp61
- dpp73
- Now answer the following :
- PHYSICS
- TRUE/FALSE