Complete Solutions to Example of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In the `HCI` molecule, the separation between the nuclei of the two atoms is about `1.27Å (1Å = 10^(-10)m)`. Find the approximate location of the c.m of the molecule, given that a chlorine atom is about `35.5` times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus ?
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionTwo particle of masses 100g and 300 g at a given time have positions `2 hat(i)+5hat(j)+13 hat(k) and -6hat(i)+4hat(j)-2hat(k)`m respectively and velocities `10 hat(i)-7hat(j)-3hat(k)and 7 hat(i)-9hat(j)+6 hat(k) "ms"^(-1)` respectively. Determine the instantaneous position and velocity of CM.
View SolutionIf three point masses `m_(1),m_(2) and m_(3)` are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View SolutionThree identical spheres each of radius `R` are placed thouching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
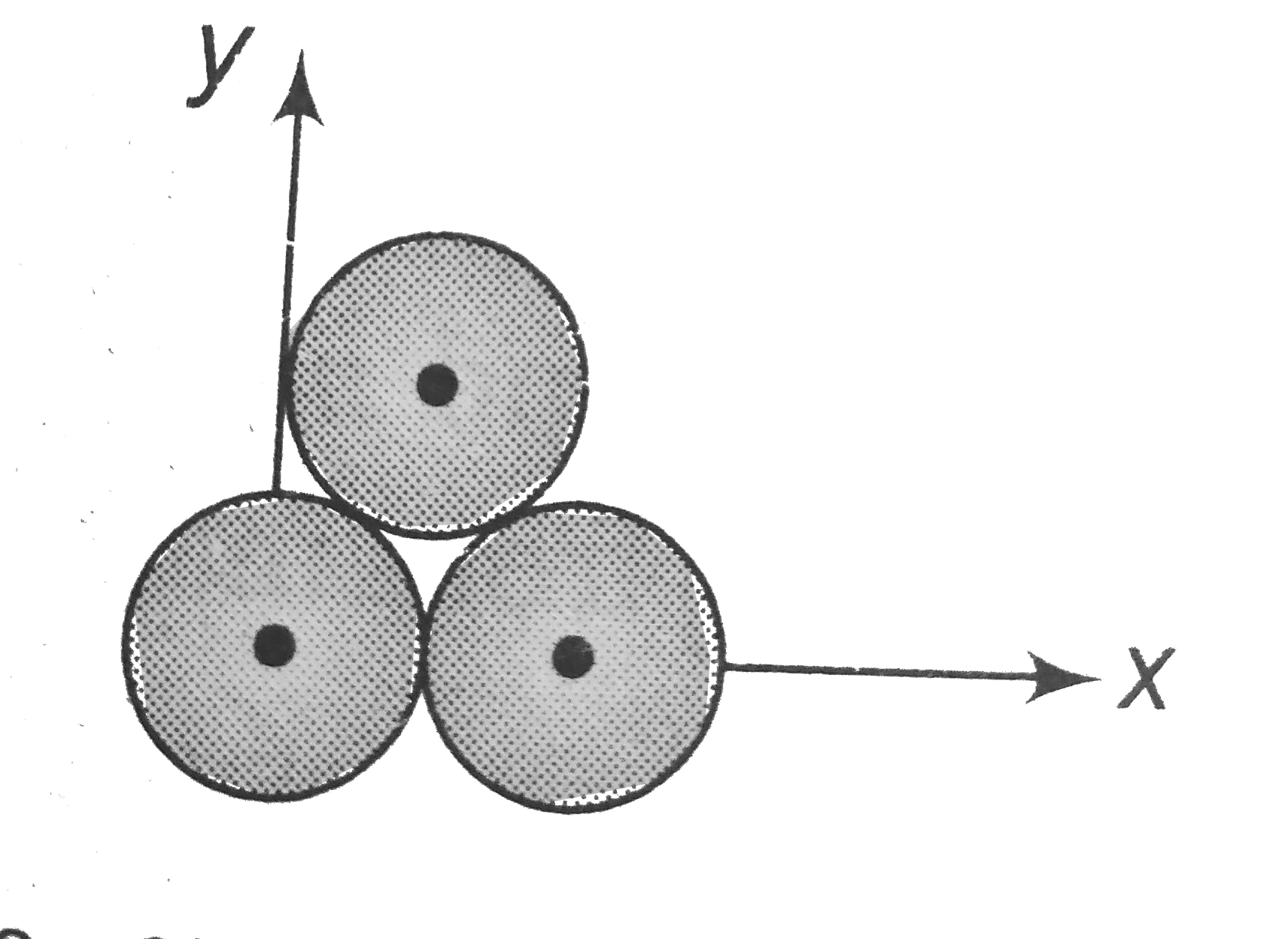 .
.
View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionFind the position of centre of mass of the T-shaped plate from `O`, in Fig.

View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionA circular plate of unifrom thickness has a diameter of `56 cm`. A circular portion of diameter `42 cm` is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA square of side `4 m` having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre `O`.
View SolutionA particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, find the tension in the string.
View SolutionA stone of mass 4 kg is attached to a string of 10 m length and is whired in a horizontal circle. The string can withstand a maximum tension of 60 N. Calculate the maximum velocity of revolution that can be given to the stone without breaking the string.
View SolutionA string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle . Calculate the greatest number of revolutions that the mass can make without breaking the string .
View SolutionA stone of mass 0.3 kg tied to the end of a string in a horizontal plane whirled in a circle of radius 1 m with a speed of `40 "rev min"^(-1)`. (i) What is the tension in thr string ? (ii) What is the maximum speed with which the stone can be whirled around if the string can withstand the maximum tension of 200 N ?
View SolutionA ball of mass `0.1kg` is suspended by a string `30 cm` long Keeping the string always taut the ball describe a horizontal circle of radius `15cm` Calculate the angular speed of the ball .
View SolutionA `70kg` man stands in contact against the inner wall of a hollow cylindrical drum of radius `3m` rotating about its verticle axis. The coefficient of friction between the wall and his clothing is `0.15` . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA thin circular wire of radius `R` rotatites about its vertical diameter with an angular frequency `omega` . Show that a small bead on the wire remain at its lowermost point for `omegalesqrt(g//R)` . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega=sqrt(2g//R)` ? Neglect friction.
View SolutionA bend in a level road has a radius of 100 m Find the maximum speed which a car turning this bend may have without skidding if coefficient of friction between the tyres and the road is 0 .8 S .
View SolutionA car of mass `1500kg` is moving with a speed of `12.5ms^(-1)` on a circular path of radius `20m` on a level road What should be the frictional force to avoid slipping of car Calculate the cofficient of friction .
View SolutionA car travels on a flat , circular track of radius `200 m` at `30 ms^(-1)` and has a centripetal acceleration `= 4 .5 ms^(-2)` . (a) If the mass of the car is 1000 kg , what frictional force is required to provide the acceleration ? (b) If the coefficient of staic friction is 0.8 , what is the maximum speed at which the car can circle the track ?
View SolutionA long plying record revolves with a speed of `33 (1)/(3) "rev min"^(-1)`, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the coefficient of friction between the coins and the record is 0.15, which of the two coins will revolve with the record ? Take `g = 9.8 ms^(-2)`.
View SolutionA train rounds an unbanked circular bend of radius 30 m at a speed of `54 km//h` The mass of the train is `10^(6)` kg What provides the centripetal force required for this purpose ? The engine or the rails ? What is the angle of banking required to prevent out the rails ?
View SolutionA train has to negotiate a curve of radius 400 m. By how much should the outer rail be raised with respect to inner rail for a speed of 48 km/hr. The distance between the rails is 1 m.
View SolutionA curve of radius 900 m is banked so that no friction is required at a speed of `30 ms^(-1)`. Calculate the angle of banking.
View SolutionAn aircraft executes a horizontal loop at a speed of `720 "kmh"^(-1)` with its wings banked at `15^(@)`. What is the radius of the loop ?
View SolutionFind the angle through which a cyclist bends when he covers a circular path `34.3 m` long in `sqrt (22)` sec . Given `g = 9.8 ms^(-2)` .
View SolutionA cyclist speeding at `18 km// h` on a level road takes a sharp circular turn of radius 3 m without reducing the speed . The coefficient of static friction between the tyres and the road is 0.1 Will the cyclist slip while taking the turn ?
View SolutionA circular racetrack of radius 300 m is banked at an angle of `15^(@)` If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
View SolutionA car is speeding on a horizontal road curving round with a radius 60 m The coefficient of friction between the wheels and the road in 0.5 The height of centre of gravity of the car from the road level is 0.3 m and the distance between the wheels is 0 .8 m . Calculate the maximum safe velocity for negotiating the curve . Will the car skid or topple if this velocity is exceeded ?
View SolutionAn electric bulb suspended from the roof of a railway train by a flexible wire shifts through an angle of `19^(@) 48` when the train goes horizontally round a curved path of `200m` radius Find the speed of the train .
View SolutionOne end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA child revolves a stone of mass 0 .5 kg tied to the end of a string of length 40 cmin a vertical circle . The speed of the stone at the lowest point of the circle is `3 m//s` Calculate tension in the string at this point.
View SolutionYou may have seen in a circus a motorcyclist driving in vertical loops inside a death well (a hollow spherical chamber with holes so the spectators can watch from outside) Explain clearly why the motorcyclist does not drop down when he is at the uppermost point of death well with no support from below What is the minimum speed required at the uppermost position to perfrom a vertical loop if the radius of the chamber is 25 m ?
View SolutionA body weighing `0.4kg` is whirled in a verticle circle making `2rps` If the radius of the circle is `1.2m` find the tension in the stringat (i) top of the circle (ii) bottom of the circle .
View SolutionA bucket containing water is tied to one end of a rope of length 2.5 m and rotated about the other end in a vertical circle so that water does not spill even when bucet is upside down . What is the maximum velocity of the bucket at which this happens ? How many rotations per minute is it making `g = 10 m//s^(2) ` .
View SolutionA body weighing 0.5 kg tied to a string is projected with a velocity of `10 ms^(-1)`. The body starts whirling in a vertical circle. If the radius of circle is 0.8 m, find the tension in the string when the body is (i) at the lop of the circle and (ii) at the bottom of the circle.
View SolutionIn a circus , the diameter of globe of death is 20 m . From what minimum height must a motor cyclist start in order to go around the globe successfully ? .
View SolutionA weightless thread can bear tension upto `3.7 kg` wt A stone of mass `500g` is tied to it and revolves in a verticle circle of radius `4m` What will be the maximum angular velocity of the stone if `g = 10 m//s^(2)` .
View SolutionAn aeroplane flying in the sky dives with a speed of `360 km//h` in a verticale circle of radius 200 m The weight of pilot sitting in it is 75 kg Calulate the force with which the pilot presses his seat when the aeroplane is (i) at the lowest position and (ii) at the highest position Take ` g = 10 m//s^(-2)` .
View SolutionOn applying a constant torque, a wheel at rest, turns through `400` radian in `10 s`. Find angular acceleration. If same torque continues to act, what will be angular veclocity of the wheel after `20 s` from stars ?
View SolutionA flywheel rotates about a fixed axis and slows down from 300 rpm to 100 rpm in 2 minutes (i) What is the angular acceleration in `"rad min"^(-2)` ? (ii) How many revolutions does the wheel complete during this time ?
View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes `n` rotations in `t` sec.., show that angular acceleration of the wheel is given by `alpha = 4pi n/t^(2) rad s^(2)`.
View SolutionThe radius of a wheel of car is `0.4m`. The car is accelerated from rest by an angular acceleration of `1.5 rad//s^(2)` for `20 s`. How much distance will the wheel cover in this time and what will be its linear velocity ?
View SolutionA body of mass 50 g is revolving about an axis in a circular path. The distance of the centre of mass of the body from the axis of rotation is 50 cm. Find the moment of inertia of the body.
View SolutionA wheel of mass 8 kg and radius of gyration 25 cm is rotating at 300 rpm. What is its moment of inertia ?
View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are located at the vertices of an equilateral triangle of side `alpha`. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_(1)?`
View SolutionThree balls of masses `1 kg, 2 kg and 3 kg` are arranged at the corners of an equilateral triangle of side `1 m`. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionFour particles of masses `4 kg, 2 kg, 3kg and 5 kg` are respectively located at the four corners `A, B, C, D` of a square of side `1 m`. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicular to the plane of the square. (ii) side `AB` (ii) diagonal `BD`.
View SolutionWhat is the moment of inertia of a ring of mass 2kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane ? Also find the moment of inertia about a parallel axis through its edge.
View SolutionThe moment of inertia of a uniform circular disc about its diameter is `100 "g cm"^(2)`. What is its moment of inertia (i) about its tangent (ii) about an axis perpendicular to its plane ?
View SolutionCalculate the moment of inertia of a circular disc of radius `10 cm`, thickness `5 mm` and uniform density `8 g cm^(-3)`, about a transverse axis through the centre of the disc.
View SolutionCalculate the moment of inertia of a cylinder of length `1.5 m`, radius `0.05m` and density `8 xx 10^(3) kg//m^(3)` about the axis of the cylinder.
View SolutionCalculate the moment of inertia of the earth about its diameter, taking it to be a sphere of `10^(25)` kg and diameter 12800 km.
View SolutionFour spheres, each of diameter `2a and mass M` are placed with their centres on the four corners of a square of side `b`. Calculate one side of the square taken as the axis.
View SolutionTwo point masses of 2kg and 10 kg are connected by a weightless rod of length 1.2 m. Calculate the `M.I.` of the system about axis pasing through the centre of mass and perpendicular to this system.
View SolutionFind the moment of inertia of a rectangular bar magnet about an axis passing through its centre and parallel to its thickness. Mass of magnet is `100 g`, its length is `12 cm`, breadth is `3 cm` and thickness is `2 cm`.
View SolutionCalculate the ration of radii of gyration of circular ring and a disc of the same radius about the axis passing through their centres and perpendicular to their planes.
View SolutionFind the radius of gyration of a rod of mass 100 g and length 100 cm about an axis passing through its centre and perpendicular to its length.
View SolutionA wheel is rotating at a speed of 1000 rpm and its `KE is 10^(6) J`. What is moment of inertia of the wheel about its axis of rotation ?
View SolutionA body of mass 2 kg is revolving in a horizontal circle of radius 2 m at the rate of 2 revolutions per second. Determine (i) moment of inertia of the body and (ii) the rotational kinetic energy of the body.
View SolutionCalculate the `KE` of rotation of a circular disc of mass `1 kg` and radius `0.2 m` rotating about an axis passing through its centre and perpendicular to its plane. The disc is making `30//pi` rotations per minute.
View SolutionAn energy of `484 J` is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Calculate moment of inertia of flywheel.
View SolutionCalculate rotational `K.E.` of earth about its own axis, taking it to be a sphere of mass `6 xx 10^(24) kg` and radius `6400 km`.
View SolutionA metre stick is is held verticaly with one end on a rough horizontal floor. It is gently alowed to fal on the floor. Assuming that the end ast the floor does not slip find the angular speed of the rod when it hits the floor.
View SolutionA uniform circular disc of mass `m` is set rolling on a smooth horizontal table with a uniform linear velocity `v`. Find the total K.E. of the disc.
View SolutionA solid sphere is rolling on a frictionless plane surface about the axis of symmetry. Find the rotational energy of the sphere. Also, find the ratio of rotational `K.E.` to total energy.
View SolutionA wheel of mass `5 kg` and radius `0.40 m` is rolling on a road without sliding with angular velocity `10 rad s^-1`. The moment of ineria of the wheel about the axis of rotation is `0.65 kg m^2`. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
View SolutionA solid cylinder rolls down an inclined plane. Its mass is `2 kg and radius 0.1 m`. It the height of the inclined plane is `4m`, what is its rotational `K.E.` when it reaches foot of the plane ? Assume that the surfaces are smooth. Take `M.I.` of solid cylinder about its axis = `mr^(2)//2`.
View SolutionA torque of `2.0 xx 10^(-4)` Nm is applied to produce an angular acceleration of `4 "rad s"^(-2)` in a rotating body. What is the moment of inertia of the body ?
View SolutionA car moves on a road with a speed of `54 km h^(-1)`. The radius of its wheels is `0.35 m`. What is the average negative torque transmitted by its brakes to the wheels if the car is brought to rest in `15 s`? Moment of inertia of the wheels about the axis of rotation is `3 kg m^(2)`.
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of `2 "rad s"^(-2)` ?
View SolutionA torque of 10 Nm is applied to a flywheel of mass 10 kg and radius of gyration 50 cm. What is the resulting angular acceleration ?
View SolutionA flywheelm of mass 150 kg and radius of gyration 3 m is rotated with a speed of 480 rpm. Find the torque required to stop it in 7 rotations.
View SolutionA rope is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ?
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. It is making 240 r.p.m. what is the torque necessary to bring it to rest in 20 s ? If the torque is due to a force applied tangentially on the rim of the flywheel, what is the magnitude of the force ?
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel ? Also find out the moment of inertia of the wheel.
View SolutionTo maintain a rotor at a uniform angular speed of `200 "rad s"^(-1)`, an engine needs to transmit a torque of 180 Nm. What is the power of the engine required ?
View SolutionA body whose moment of inertia is `3 "kgm"^(2)`, is at rest. It is rotated for 20 s with a moment of force 6 Nm. Find the angular displacement of the body. Also calculate the work done.
View SolutionHow much tangential force would be needed to stop the earth in one year, if it were rotating with angular velocity of `7.3 xx 10^(-5) "rad s"^(-1)` ? Given the moment of inertia of the earth `=9.3 xx 10^(37) "kg m"^(2)` and radius of the earth `=6.4 xx 10^(6)` m.
View SolutionThe angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycles per second. Calculate the moment of inertia of the body about the axis of rotation.
View SolutionA 40 kg flywheel in the formof a uniform circlular disc of 1m radius is making 120 rpm. Calculate the angular momentum.
View SolutionA solid cylinder of mass `20 kg` rotates about its axis with angular speed `100 s^(-1)`. The radius of the cylinder is `0.25 m`. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
View SolutionA ring of diameter 0.4 m and of mass 10 kg is rotating about its axis at the rate 2100 rpm. Find (i) moment of inertia (ii) angular momentum and (iii) rotational K.E. of the ring.
View SolutionAn electron of mass `9 xx 10^(-31)` kg revolves in a circle of radius 0.53 Å around the nucleus of hydrogen with a velocity of `2.2 xx 10^(6) "ms"^(-1)`. Show that its angular momentum is equal to `h//2pi`, where `h` is Plank's constant of value `6.6 xx 10^(-34) Js`.
View SolutionCalculate the angular momentum of the earth rotating about its own axis. Mass of the earth `= 5.98 xx 10^(27)` kg, mean radius of the earth `=6.37 xx 10^(6)m,M.I` of the earth `= (2)/(5)MR^(2)`.
View SolutionShow that angular momentum of a satellite of mass `M_(s)` revolving around earth of mass `M_(e)` in an orbit of radius `r` is `sqrt(GM_(s)^(2)M_(e)r)`.
View SolutionA small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm ? Neglect friction.
View SolutionA star of mass twice the solar mass and radius `10^(6)` km rotates about its axis with an angular speed of `10^(6) "rad s"^(-1)`. What is the angular speed of the star when it collapses (due to inward gravitational force) to a radius of `10^(4)` km ? Solar mass `1.99 xx 10^(30)` kg.
View Solution(i) A child stands at the centre of turntable with his two arms out stretched. The turntable is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to `(2)/(3)` times the initial value ? Assume that the turntable rotates without friction
(ii) Show that the child's new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy ?
View SolutionIf the earth were to suddenly contract to half of its present radius (without any external torque on it), by what duration would the day be decreased ? Assume earth to be perfect solid sphere of radius `(2)/(5)MR^(2)`.
View SolutionWhat will be the duration of the day, if earth suddenly shrinks to 1/64 of its original volume, mass remaining the same ?
View SolutionThe maximum and minimum distances of a comet from the sun are `1.4 xx 10^(12) m and 7 xx 10^(10)` m. If is velocity nearest to the sun is `6 xx 10^(4) ms^(-1)`, what is the velocity in the fartest position ? Assume that path of the comet in both the instantaneous positions is circular.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega`. Another disc of the same dimension but of mass M/4 is placed gently on the first disc coaxially. Show that the angular momentum of the system is `(4)/(5)omega`.
View SolutionA horizontal disc rotating about a vertical axis passing through its centre makes 180 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 8 cm from its axis. If the frequency is thus reduced to 150 rpm, calculate the moment of inertia of the disc.
View SolutionTwo discs of moments of inertia `I_(1) and I_(2)` about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed `omega_(1) and omega_(2)` are brought into contact face to face with their axes of rotation coincident (i) What is the angular speed of the two-disc system ? (ii) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take `omega_(1) ne omega_(2)`.
View SolutionA body of mass 5 kg is attached to a weightless string wound round a cylinder of mass 8 kg and radius 0.3 m. The body is allowed to fall. Calculate (i) tension in the string (ii) acceleration with which the body falls and (iii) the angular acceleration of the cylinder.
View SolutionA cylinder of mass 5kg and radius 30 cm is rolling down an inclined place at an angle of `45^(@)` with the horizontal. Calculate (i) force of friction, (ii) acceleration with which the cylinder rolls down and (iii) the minimum value of static friction so that cylinder does not slip while rolling down the plane.
View SolutionA solid cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination `30^(@)`. The coefficient of static friction, `mu_(s)=0.25` (i) Find the force of friction acting on the cylinder. (ii) What is the work done against friction during rolling ? (iii) If the inclination `theta` of the plane is increases, at what value of `theta` does the cylinder begin to skid, and not roll perfectly ?
View SolutionA ring, a disc and a sphere all of the same radius and mass roll down an inclined plane from the same height `h`. Which of the three reaches the bottom (i) earliest (ii) latest ?
View SolutionA solid cylinder of radius 4 cm and mass 250 g rolls down an inclined plane (1 in 10). Calculate the acceleration and the total energy of the cylinder after 5 s.
View Solution
Example questions and complete solutions for chapter ROTATIONAL MOTION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11