Complete Solutions to Problem for self practice of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| SL ARORA | Problem for self practice |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
The distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is `1.1 Å`. Given, mass of carbon atom is 12 a.m.u. and mass of oxygen atom is 16 a.m.u., calculate the position of the centre of mass of the carbon monoxide molecule
View SolutionThree particles of msses 1.0 kg , , 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionTwo bodies of masses 10 kg and 2 kg are moving with velocities `2 hat(i)-7 hat(j)+3 hat(k)` and `-10 hat(i)+35 hat(j)-3hat(j) ms^(-1)` respectively. Find the velocity of the centre of mass of the system.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
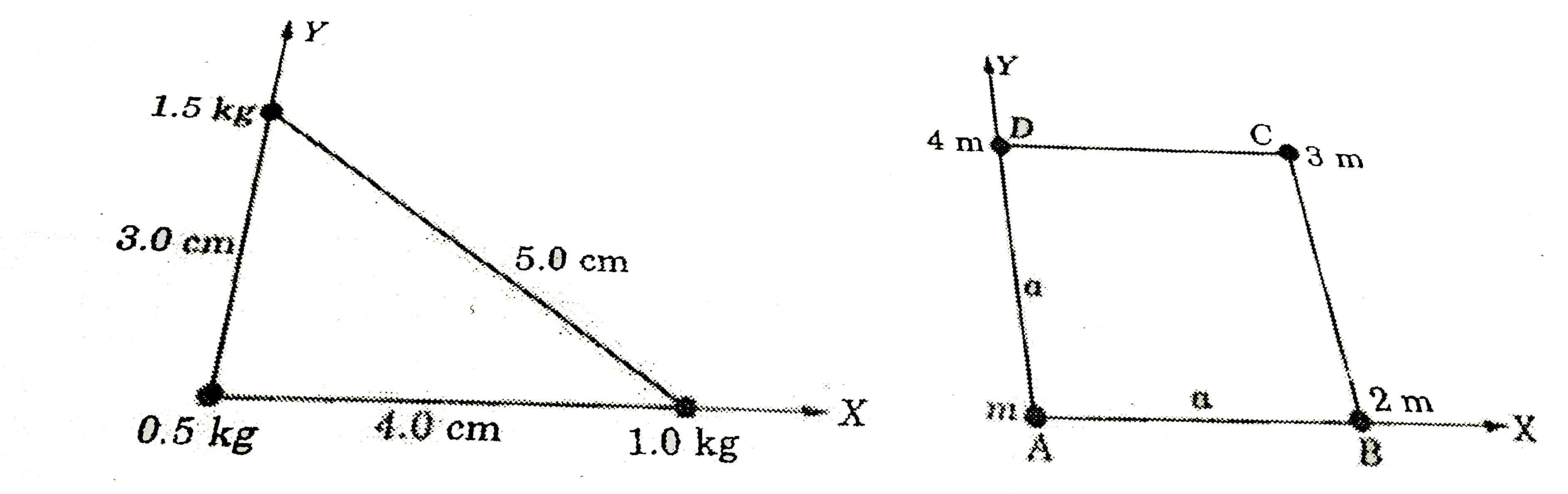
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionTwo bodies of masses 2 kg and 1 kg are moving along the same line with speeds `2ms^(-1)` and `5 ms^(-1)` respectively. What is the speed of the centre of mass of the system if the two bodies are moving (i) in same direction and (ii) in opposite directions?
View SolutionThe mass per unit length `(lambda)` of a non-uniform rod varies linearly with distance x from its one end accrding to the relation, `lambda = alpha x`, where `alpha` is a constant. Find the centre of mass as a fraction of its length L.
View SolutionThe centre of mass of three particles of masses `1kg, 2 kg` and `3kg` lies at the point (3m, 3m, 3m). Where should a fourth particle of mass 4 kg be positioned so that the centre of mass of the four particle system lies at the point (1m, 1m, 1m)?
View SolutionFrom a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is `alpha`

View SolutionA 100 g weight is tied at the end of a string and whirled around in horizontal circle of radius 15 cm at the rate of 3 revolutions per second. What is the tension in the string?
View SolutionA gramophone disc rotates at 60 rpm. A coin of mass 18 g is placed at a distance of 8 cm from the centre. Calculate the centrifugal force on the coin. Take `pi^(2) = 9.87`.
View SolutionA string can withstand a tension of 25 N. What is the greatest speed at which a body of mass 0.5 kg can be whirled in a circle using 0.5 m length of the string ? Neglect the force of gravity on the body.
View SolutionA ball of mass 100 g is suspended by a string `40 cm` long. Keeping the string taut, the ball describes a horizontal circle of radius 10 cm. Find the angular speed.
View SolutionFind the maximum speed at which a car can take turn round a curve of 30 cm radius on a level road if the coefficient of friction between the tyres and the road is 0.4. Take `g = 10 ms^(-2)`.
View SolutionWhat should be the coefficient of friction between the tyres and the road, when a car travelling at `60 km h^(-1)` makes a level turn of radius `40 m` ?
View SolutionThe mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of `10 ms^(-1)`. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take `g = 10 ms^(-2)`.
View SolutionA cyclist riding at a speed of `14sqrt(3) ms^(-1)` takes a turn around a circular road of radius `20 sqrt(3)m`. What is the inclination to the vertical?
View SolutionA cyclist speeding at `6ms^(-1)` in a circle of 18 m radius makes an angle `theta `with the vertical. Calculate `theta`. Also determine the minimum possible value of the coefficient of friction between the tyres and the ground?
View SolutionA motor cyclist goes round a circular race course of diameter 320 m at `144 km h^(-1)`. How far from the vertical must he lean inwards to keep his balance? Take `g = 10 ms^(-2)`.
View SolutionAn aeroplane travelling at a speed of `500 km h^(-1)` tilts at an angle of `30^(@)` as it makes a turn. What is the radius of the curve?
View SolutionFor traffic moving at `60 kmh^(-1)`, if the radius of the curve is `0.1 km`, what is the correct angle of banking of the road? Take `g = 10ms^(-2)`.
View SolutionA railway carriage has its CG at a height of 1 m above the rails , which are 1 m apart . Calculate the maximum safe speed at which it can travel round an unbanked curve of radius 80 m .
View SolutionA curve in a road forms an arc of radius 800 m. If the road is 19.6 m wide and outer edge is 1m higher than the inner edge, calculate the speed for which it is banked.
View SolutionA trains has to negotiate a curve of radius `400 m`. By how much should the outer rail be raised with respect to the inner rail for a for a speed of `48 km h^(-1)` ? The distance between the rails is 1m.
View SolutionThe radius of curvature of a railway track at a place where the train is moving at a speed of `72 kmh^(-1)` is `625m`. The distance between the rails is 1.5 m. Find the angle and the elevation of the outer rail so that there may be no side pressure on the rails, Take `g = 9.8 ms^(-2)`.
View SolutionThe CG of a taxi is 1.5 m above the ground and the distance between its wheels is 2m. What is the maximum speed with which it can go round an unbanked curve of radius 100 m without being turned upside down ? What minimum value would the coefficient of friction needed at this speed?
View SolutionA train is moving with a speed of `72 kmh^(-1)` on a curved railway line of `400 m` radius. A spring balance loaded with a block of weight 5 kg is suspended from the roof of the train. What would be the reading of the balance? Take `g = 10 ms^(-2)`.
View SolutionA 2000 kg car has to go over a turn whose radius is `750 m` and the abgle of slopw is `5^(@)`. The coefficient of friction between the wheels and the road is 0.5. What should be the maximum speed of the car so that it may go over the turn without slipping ?
View SolutionA body weighing 0.5 kg tied to a string is projected with a velocity of `10 ms^(-1)`. The body starts whirling in a vertical circle. If the radius of circle is 0.8 m, find the tension in the string when the body is (i) at the lop of the circle and (ii) at the bottom of the circle.
View SolutionA stone is tied to a weightless string and revolved in a vertical circle of radius 5 m . What should be the minimum speed of the stone at the highest point of the circle so that the string does not slack ? What should be the speed of the stone at the lowest point of vertical circle ? Take ` g = 9.8 ms^(2) ` .
View SolutionA bucket containing 4 kg of water , is tied to a rope of length 2.5 m and rotated in a vertical circle in such a way that the water in upside down position What is the speed of the bucket at (a) highest point and (b) lowest point of its circular path ? Take ` g= 10 m//s ` .
View SolutionA stone of mass 0.3 kg is tied to one end of a string 0.8 m long and rotated in a vertical circle. At what speed of the ball will the tension in the string be zero at the highest point of the circle? What would be the tension at the lowest point in this case ? Given `g = 9.8 ms^(-2)` ?
View SolutionIn a circus, a motor cyclist goes round a vertical circle inside a spherical cage of radius `4.5 m`. Calculate the minimum speed of the motor cycle inside the cage.
View SolutionWhat is the minimum speed required at the bottom to perform a vertical loop, if the radius of the death-well in a circus is 25m?
View SolutionA ball rolls down an inclined plane from a height and then goes round a vertical circle of radius 1m. What should be the height of the inclined plane so that the ball is able to go round the circle without leaving the track?
View SolutionThe railway bridge over a canal is in the form of an arc of a circle of radius 20m. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point ? Take `g = 9.8 ms^(-2)`
View SolutionAn aeroplane describes a vertical circle when looping. Find the radius of the greatest possible loop if the velocity of the aeroplane at the lowest point of its path is `50 ms^(-1)`. Take `g = 10 ms^(-2)`.
View SolutionA gridstone has a constant acceleration of `4 rad s^(-1)`. Starting from rest, calculate the angular speed of the grindstone 2.5 s later.
View SolutionThe speed of a motor increases from 600 rpm to 1200 rpm in 20 s. What is the angular acceleration and how many revolution does it make during this time ?
View SolutionOn application of a constant torque, a wheel is turned from rest through an angle of `200` radius in `8 s`. What is its angular acceleration ? If the same torque continues to act, what will be the angular velocity of the wheel `16 s` from the start ?
View SolutionThe motor of an engine is erotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assumgn cnstant angular decelertion, calculate the number of revolutions made by it before coming to rest.
View SolutionA car is moving at a speed of `72 kmh^(-1)`. The diameter of its wheel is 0.50m. If the wheels are stopped in 20 rotations by applying brakes, calculate the angular retardation produced by the brakes.
View SolutionFind the moment fo inertia of the hydrogen molecules about an axis passing through its centre of mass and perpendicular to the internuclear axis. Given mass of H-atom `= 1.7 xx 10^(-27) kg`, interatomic distance `= 4xx 10^(-10)m`
View SolutionThree point masses, each of mass `m`, are placed at the corners of an equilateral triangle of side `L`. The moment of inertia of this system about an axis along one side of the triangle is
View SolutionFour point masses of 20 g each are placed at the corners of a square ABCD of side 5 cm, as shown in Fig. 8.48. find the moment of inertia of the system (i) about an axis coinciding with the side BC and (ii) about an axis through A and perpendicular to the plane of the square.

View SolutionThe point masses of 0.3 kg, 0.2 kg and 0.1 kg are placed at the corner of a right angles `Delta ABC`, as shown in Fig. 8.49. find the moment of inertia of the system (i) about an axis through A and perpendicular to the plane of the diagram and (ii) about an axis along BC.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionFour point masses of 5 g each are placed at the four corners fo a square of side 10 cm. Find the moment of inertia of the system (i) about an axis coinciding with one of the sides and (ii) about an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square.
View SolutionFour particles each of mass m are kept at the four corners of a square of edge a. Find the moment of inertia of the system about an axis perpendicular to the plane of the system and passing through the centre of the square.
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionCalculate moment of inertia of a uniform circular disc of mass `700 g` and diameter `20 cm` about
(i) an axis through the centre of disc and perpendicular to its plane, (ii) a diameter of disc, (iii) a tangent in the plane of the disc, (iv) a tangent perpendicular to the plane of the disc.
View SolutionThe moment of inertia of a circular ring about the tangent to the ring which is parallel to a diameter of the ring is `15 g cm^(2)`. If the mass of the ring is 2g, what is its radius?
View SolutionUsing theorem of parallel axes, calculate the moment of inertia of a disc of mass 400 g and radius 7 cm about an passing through its edge and perpendicular to its plane.
View SolutionCalculate the moment of inertia of sphere of diameter 20 cm about a tangent to the sphere. Given density of copper `= 8.9 g cm^(-3)`.
View SolutionA sphere of mass 1 kg has a radius of 10 cm. Calculate the moment of inertia (i) about the diameter and (ii) about the tangent.
View SolutionThe radius of a sphere is 5 cm. Calculate the radius of gyration about (i) its diameter and (ii) about any tangent.
View SolutionCalculate the radius of gyration of a cylindrical rod of mass M and length L about an axis of rotation perpendicular to its length and passing through its centre.
View SolutionTwo masses of 3 kg and 5 kg are placed at 30 cm and 70 cm marks respectively on a light wooden meter scale, as shown in Fig. 8.51. what will the moment of inertia of the system about an axis through (i) 0 cm mark and (ii) 100 cm mark, and perpendicular to the meter scale?

View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 0.5 m in each of the following cases, as shown in Fig. 8.52.

View SolutionA circuit disc of mass 49 kg and of radius 50 cm is mounted axially and made to rotate. Calculate the K.E.. It possesses, when executing 120 rpm
View SolutionA flywheel of mass 500 kg and diameter 1 m makes 500 rpm. Assuming the mass to be concentrated along the rim, calculate (i) angular velocity (ii) moment of inertia and (ii) rotational K.E. of the flywheel.
View SolutionA rod revlving 60 times in a minute about an axis passing through an end at right angles to the length, has kinetic energy of 400 J. find the moment of inertia of the rod.
View SolutionA disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of `10 ms^(-1)`. Calculate the K.E. of the disc.
View SolutionA disc of mass 100 g is rolling without slipping on a horizontal surface with a velocity of `10 cm s^(-1)`. Calculate its total energy.
View SolutionA solid sphere of mass 0.1 kg and radius 2.5 cm rolls without sliding with a uniform velocity of `0.1 ms^(-1)` along a straight line on a smooth horizontal table. Find its total energy.
View SolutionA thin metal hoop of radius `0.25 m` and mass `2 kg` stars from rest and rolls down an inclined plane. If its linear velocity on reaching the foot of the plane is `2 m//s`, what is its rotational `KE` at that instant ?
View SolutionThe earth has a mass of `6 xx 10^(24) kg` and a radius of `6.4 xx 10^(6)m`. Calculate the amount of work that must be done to slow down its rotation so that duration of day becomes `30` hrs instead of 24 hours.
Moment of inertia of earth `= (2)/(5)MR^(2)`.
View SolutionThe moment of inertia of a flywheel is `4 kg m^(2)`. What angular acceleration will be produced in it by applying a torque of 10 Nm on it?
View SolutionThe moment of inertia of a body is `2.5 kg m^(2)`. Calculate the torque required to produce an angular acceleration of `18 rad s^(-2)` in the body.
View SolutionA grindstone has a moment of inertia of `50 kg m^(2)`. A constant couple is applied and the grindstome is found to have a speed of 150 rpm 10 s after starting from rest. Calculate the torque applied.
View SolutionA flywheel of moment of inertia `10^(7) g cm^(2)` is rotating at a speed of 120 rotations per minute. Find the constant breaking torque required to stop the wheel in 5 rotations.
View SolutionIf a constant torque of 500 Nm turns a wheel of moment of inertia `100 kg m^(2)` about an axis through its centre, find the gain in angular velocity in 2s.
View SolutionA sphere of mass 2 kg and radius 5 cm is rotating at the rate of 300 rpm. Calculate the torque required to stop it in 6.28 it in 6.28 revolution. Moment of inertia of the sphere about any diameter `=2/5 MR^(2)`
View SolutionDetermine the angular momentum of a car of mass 1500 kg moving in a circuit truck of radius 50 m with a speed of `40 ms^(-1)`.
View SolutionA body of mass 1.0 kg is rotaing on a circular path of diameter 2.0 m at the rate of 10 rotations in 31.4 s. calculate (i) angular momentum of the body and (ii) rotational kinetic energy.
View SolutionMass of an electron is `9.0xx10^(-31) kg`. It revolves around the nucleus of an atom in a circular orbit of radius `4.0 Å` with a speed of `6.0 xx10^(6) ms^(-1)`. Calculate the angular momentum of the electron.
View SolutionA circular ring of diameter 40 cm and mass 1 kg rotating about an axis normal to its plane and passing through the centre with frequency of 10 rotations per second. Calculate the angular momentum about its axis of rotation.
View SolutionAn ice skater spins with arms outstreched at 1.9 rps. Her moment of inertis at this instant is `1,33 kg m^(2)`. She pulls in her arms to increase her rate of spin. If the moment of inertia is `0.48 kg m^(2)` after she pulls in her arms, what is her new rate of rotation?
View SolutionA mass of 2 kg is rotating on a circular path of radius 0.8 m with angular velocity of `44 rad s^(-1)`. If the radius of the path becauses `1.0` m, what will be the value of angular velocity?
View SolutionA ball tied to a string takes us to complete revolution along a horizontal circle. If, by pulling the cord, the radius of the circle is reduceed to half of the previous value, then how much time the ball will take in one revolution?
View SolutionThe sun rotates round itself once in 27 days. What will be period of revolution if the sun were to expand to twice its present radius? Assume the sun to be a sphere of uniform density.
View SolutionIf the earth suddenly contracts by one-fourth of its present radius, by how much would the day be shortened?
View SolutionProve that for an earth satellite, the ratio of its velocity at apogee (when farthest from the earth) to its velocity at perigee (when nearest to the earth) is the inverse ratio of its distances from apogee and perigee.
View SolutionA uniform disc rotating freely about a vertical axis makes 90 revolutions per minute. A small piece of wax of mass m gram falls vertically on the disc and sticks to it at a distance of r cm from the axis. If the number of rotations per minute reduces to 60, find the moment of inertia of the disc.
View SolutionA horizontal disc rotating about a vertical axis makes 100 revolutions per minute. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis. If the number of revolutions per minute is thereby reduced to 90, calculate the moment of inertia of disc.
View SolutionA body of mass 2 kg is attached to a weightless string wound round a cylinder of mass 5 kg and radius 50 cm. the body is allowed to fall. Calculate (i) tension in the string (ii) acceleration with which the body falls.
View SolutionA solid cylinder of mass 10 kg is rolling perfectly on a plane of inclination `30^(@)`. Find the force of friction between the cylinder and the surface of the inclined plane.
View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of `30^(@)` with the horizontal. Calculate (i) force of friction, (ii) aaceleration with which the cylinder rolls down and (iii) the minimum value of corfficient of friction so that cylinder does not slip while rolling down the plane.
View SolutionIf a sphere rolls (starting from rest) in 5.3 s along a plane 1m in length of which the upper end is raised above the lower. Find the acceleration due to gravity.
View Solution
Problem for self practice questions and complete solutions for chapter ROTATIONAL MOTION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11