Complete Solutions to Problems from competitive examinations of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| SL ARORA | Problems from competitive examinations |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
An ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are `Q_1=5960J, Q_2=-5585J, Q_3=-2980J and Q_4=3645J`, respectively. The corresponding quantities of work involved are `W_1=2200J, W_2=-825J, W_3=-1100J and W_4` respectively.
(1) Find the value of `W_4`.
(2) What is the efficiency of the cycle
View SolutionA vertical hollow cylinder contains an ideal gas. The gas is enclosed by a `5kg` movable piston with an area of cross-section `5 xx 10^(-3)m^(2)`. Now, the gas is heated slowly from `300K` to `350K` and the piston rises by `0.1m`. The piston is now clamped at this position and the gas is cooled back to `300K`. Find the difference between the heat energy added during heating process and energy lost during the cooling process. `("1atm pressure" = 10^(5)Nm^(-2)]`
View SolutionThe pressure of one gram mole of a monoatomic gas increases linearly from `4xx10^(5)N//M^(2)` to `8xx10^(5)N//m^(2)`. Calculate
(i) Work done by the gas,
(ii) increase in internal energy, (iii) amount of heat supplied,
(iv) molar heat capacity of the gas.
Take `R=8.31J mol e^(-1)K^(-1)`.
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area `4 xx 10^(-3)m^(2)`. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does `50J` of work in moving the piston through a distance `0.10m`. The temperature of the gas increases by `50K`. Calculate the spring constant and the heat supplied by the heater. `P_(atm) = 1 xx 10^(5)N//m^(2)R = 8.314 J//mol-K`
View SolutionThe temperatures `T_(1) and T(2)` of two heat reservoirs in an ideal carnot engine are `1500^(@)C and 500^(@)C`. Which of these (a) increasing `T_(1) by 100^(@)C` or (b) decreasing `T_(2) by 100^(@)C` would result in greater improvement of the efficiency of the engine?
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure `P_i,` If the same gas is expanded adiabatically to a volume 2V, the final pressure `P_a.` The ratio of the specific heats of the gas is 1.67. The ratio `(P_a)/(P_1)` is .......
View SolutionAn ideal gas having initial pressure P, volume V and temperature T is allowed to expands adiabatically until its volume becomes 5.66V while its temperature falls to T/2.
(i) How many degrees of freedom do the gas molecules have?
Obtain the work done by the gas during the expansion as a function of the initial pressure P and volume V.
View SolutionAt `27^@C` two moles of an ideal monoatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas, (ii) change in its internal energy, and (iii) the work done by the gas during this process.
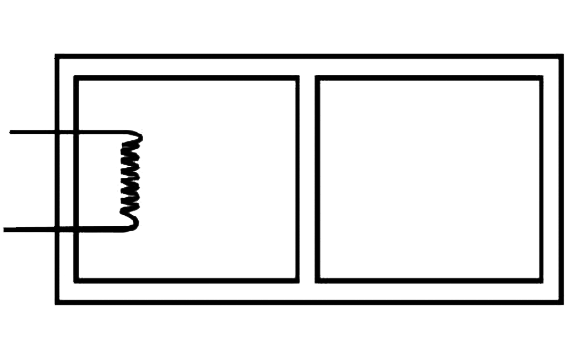
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas `(lambda=5//3)` at a pressure `P_0`, volume `V_0` and temperature `T_0`. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes `243P_0//32`. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
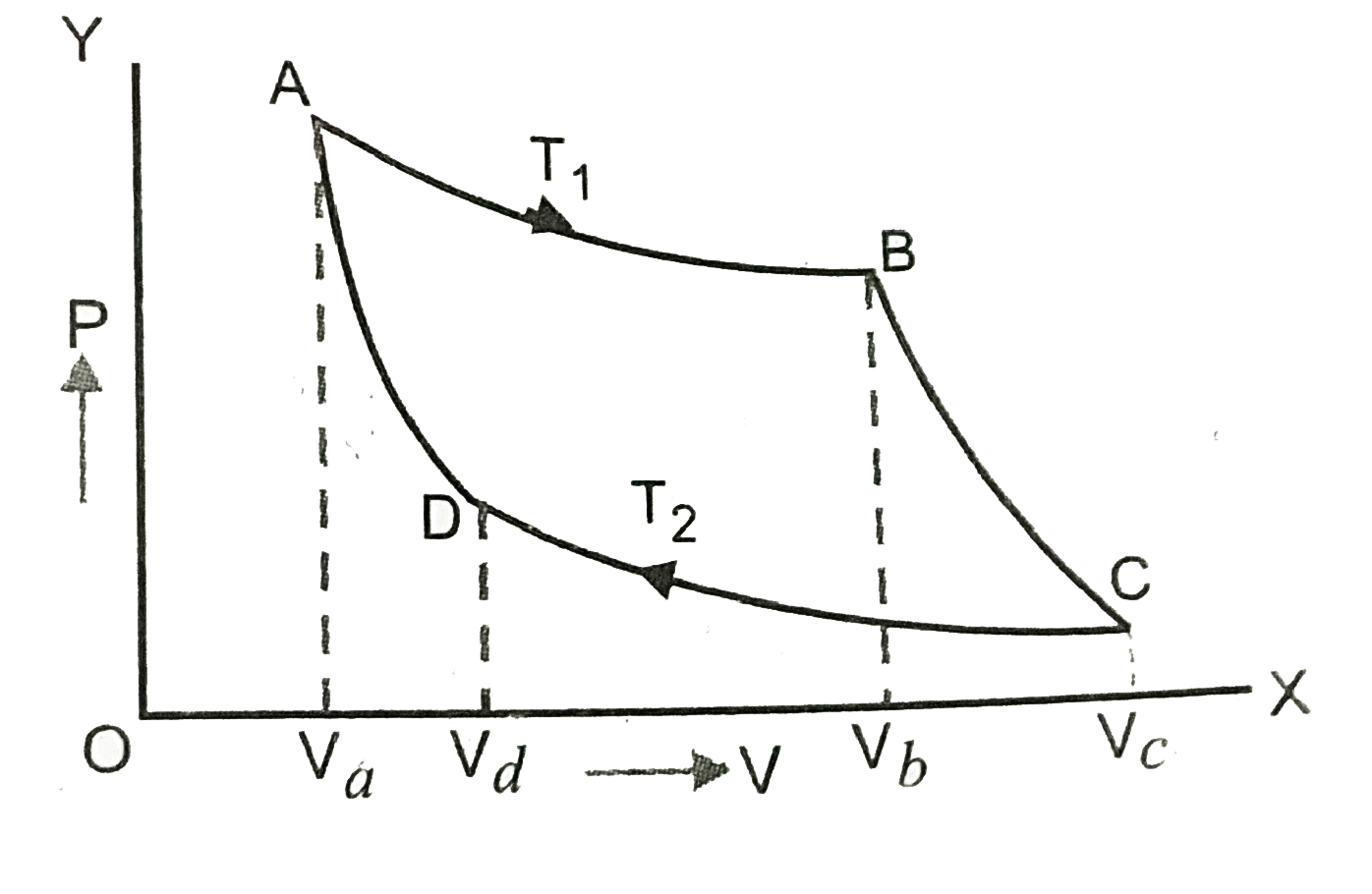
View SolutionTwo different adiabatic curves for the same gas intersect two isothermals at `T_(1), and T_(2)` as shown in `P-V` diagram, (figure). How does the ratio `(V_(a)//V_(d))` compare with the ratio `(V_(b)//V_(c))` ?
View Solution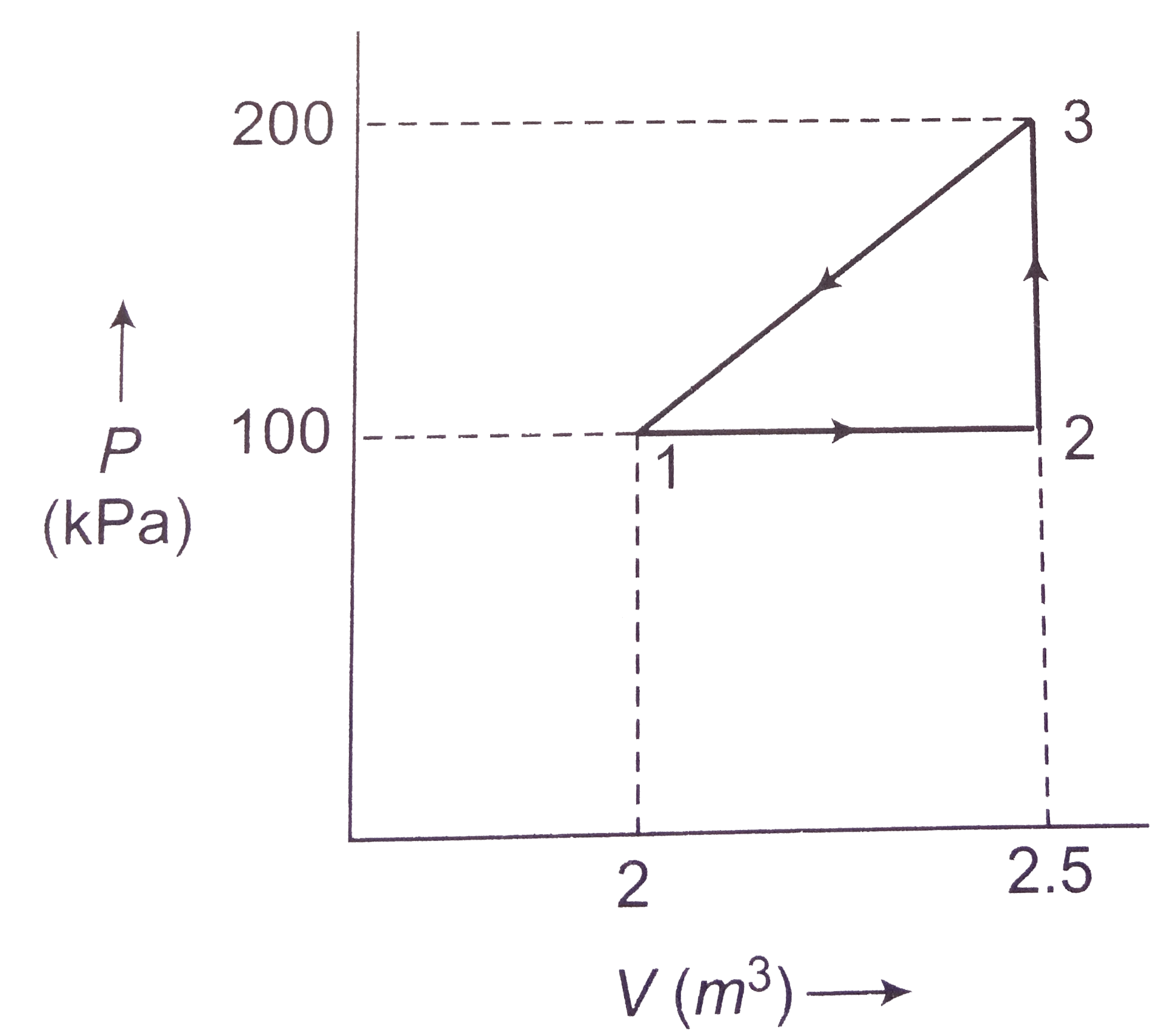
In the figure an ideal gas changes is state from state A to state C by two paths ABC and AC.
(a) Find the path along which the work done is least.
(b) The internal energy of the gas at A is 10 J and the amount of heat supplied to change its state to C through the path AC is 200 J. Calculate the internal energy at C.
(c) The internal energy of the gas at state B is 20 J. Fid the amount of the heat supplied to gas to go from A to B.
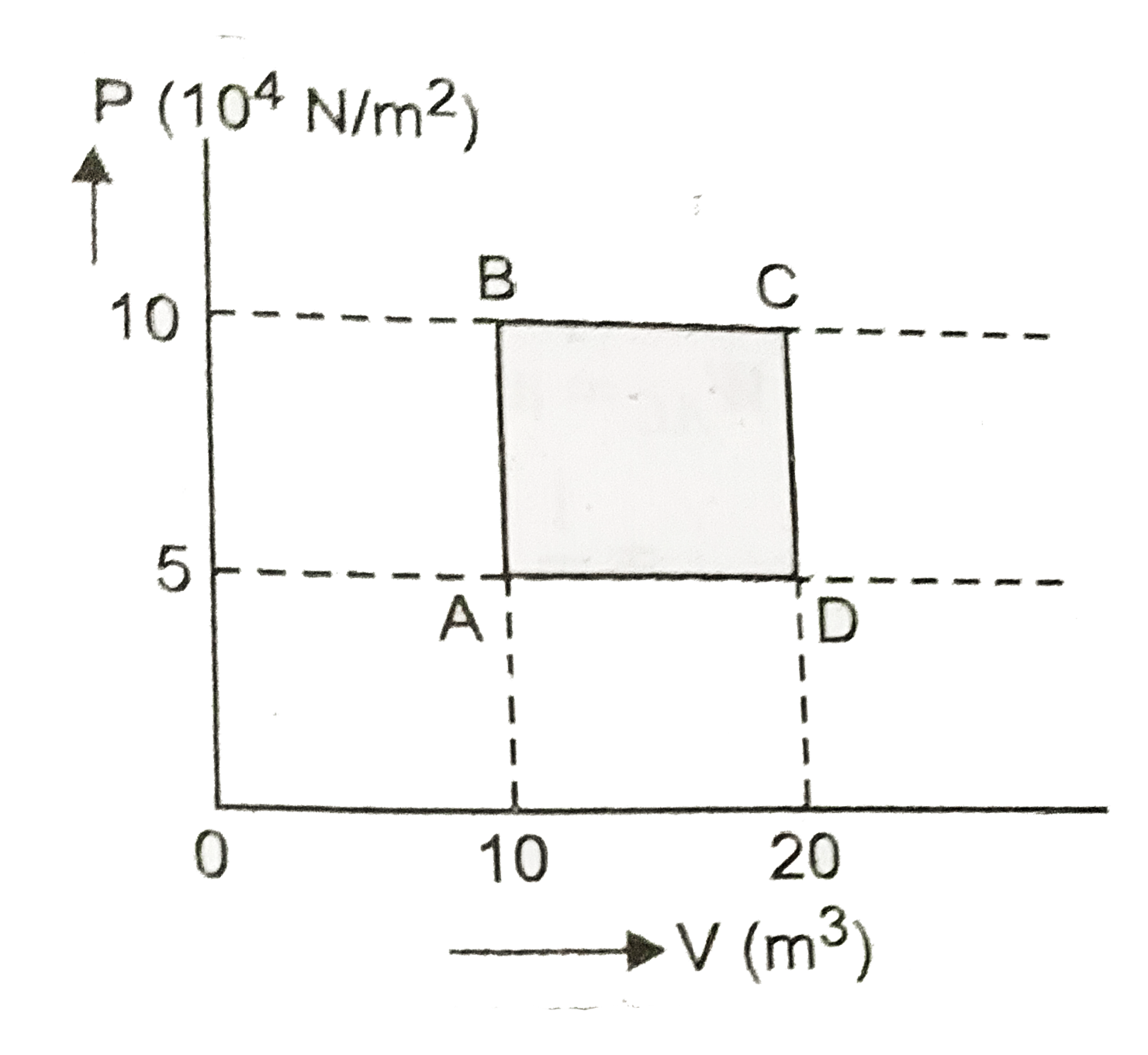
View SolutionA sample of `2 kg` of monoatomic helium (assumed ideal) is taken through the process ABC and another sample of `2 kg` of the same gas is taken through the process ACD as shown in (figure). Given molecular mass of He `= 4 and R = 8.3J mol e^(-1)K^(-1)`
(i) What is the temperature of `He` in each of the states A, B, C and D?
(ii) How much is the heat involves in process , ABC and ADC?
View SolutionOne mole of a diatomic ideal gas `(gamma=1.4)` is taken through a cyclic process starting from point A. The process `AtoB` is an adiabatic compression, `BtoC` is isobaric expansion, `CtoD` is an adiabatic expansion, and `DtoA` is isochoric. The volume ratios are `V_A//V_B=16 and V_C//V_B=2` and the temperature at A is `T_A=300K`. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
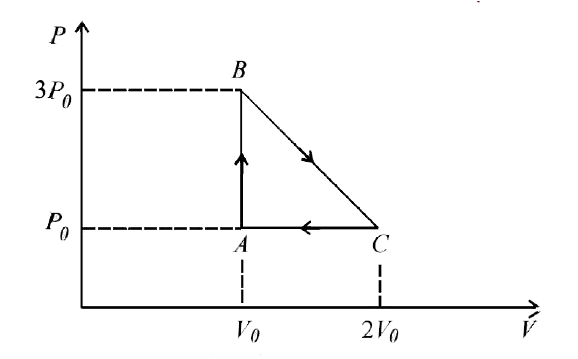
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.
View SolutionTwo moles of an ideal monoatomic gas, initially at pressure `p_1` and volume `V_1`, undergo an adiabatic compression until its volume is `V_2`. Then the gas is given heat Q at constant volume `V_2`.
(i) Sketch the complete process on a p-V diagram.
(b) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of `p_1,V_1,V_2, Q and R`]
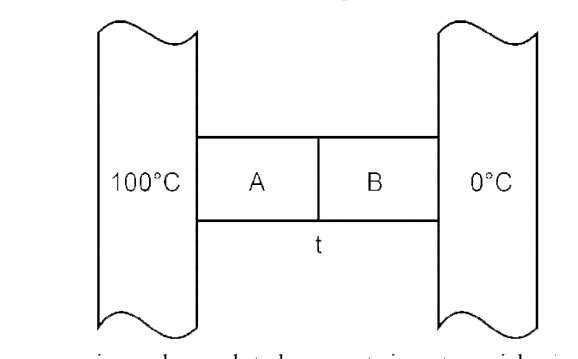
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are `300W//m ^@C and 200 W//m^@C,` respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionOne end of a copper rod of uniform cross-section and of length 3.1 m is kept in contact with ice and the other end with water at `100° C` . At what point along it's length should a temperature of `200° C` be maintained so that in steady state, the mass of ice melting be equal to that of the steam produced in the same interval of time. Assume that the whole system is insulated from the surroundings. Latent heat of fusion of ice and vaporisation of water are 80 cal/gm and 540 cal/gm respectively

View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_(1)` is surrounded by cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal con-ductivity `K_(2)` The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View Solution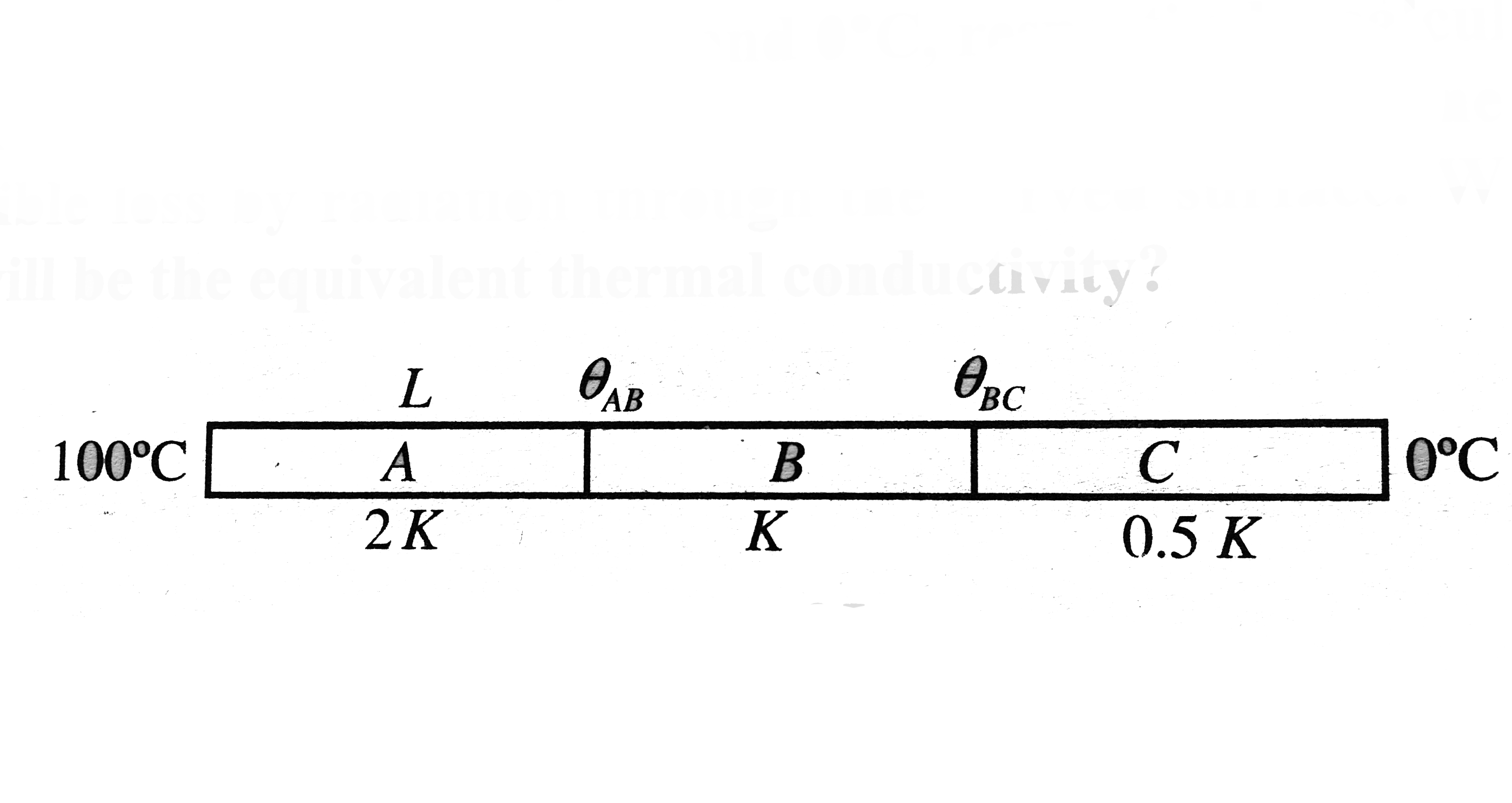
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at `100^@C` and `0^@C`, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View SolutionAn electric heater is used in a room of total wall area `137m^(2)` to maintain a temperature of `+20^(@)C` inside it when the outside temperature is `-10^(@)C`. The walls have three different layers materials . The innermost layer is of wood of thickness 2.5 cm, in the middle layer is od cement of thickness 1.0 cm and the outermost layer is of brick of thickness 25.0 cm. find the power of the electric heater. Assume that there is no heat loss through the floor and the ceiling. The thermal conductives of wood, cement and brick are `0.125, 1.5 and 1.0 watt//m// .^(@)C` respectively.
View SolutionA cylindrical block of length 0.4 m and area of cross-section `0.04 m^2` is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is `10 "watt"// m.K ` and the specific heat of the material of the disc is `600J//kg.K`, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionA wire of length 1 m and radius `10^-3`m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is `pi^@xx10^-8` ohm m and its temperature coefficient of resistance is `7.8xx10^(-3)//C` (stefan's constant`sigma=5.68xx10^-8W//m^(2) K^(2)`.
The current in the wire is nearly
View Solution
Problems from competitive examinations questions and complete solutions for chapter THERMODYNAMICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11