Complete Solutions to Exercise of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Thermodynamics |
| SL ARORA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An ideal monoatomic gas is taken around the cycle ABCDA, wher co-ordinates of A, B, C and D on and D on `P-V` diagram are A`(p,V), B(2p,V), C(2p, 2V) and D(p, 2V)`. Calculate work done during the cycle.
View SolutionCalculate net work done by the gas whose thermodynamical behaviour is represented by right angled triangle ABC on `P-V` diagram. The `P-V` diagram co-ordinates are : `A(20, 6), B(10, 12)` and `C(10, 6)` where `P` is in `Nm^(-2)` and `V` is in `m^(3)`
View SolutionCalculate the change in internal energy of a block of copper of mass `200g` when it is heated from `25^(@)C t o 75^@C`. Given specific heat of copper `= 0.1 cal. g^(-1) .^(@)C^(-1)` and assume that change in volume is negligible.
View SolutionOne kg of water at `373K` is converted into steam at the same temperature. The volume `1 cm^(3)` of water becomes `1671 cm^(3)` on boiling. Calculate the change in internal energy of the system , if heat of vaporisation is `540 cal g^(-1)`. Given standard atmospheric pressure `=1.013xx10^(5) Nm^(-2)`.
View SolutionCalculate the change in internal energy when 5g of air is heated from `0^(@)` to `4^(@)C`. The specific heat of air at constant volume is `0.172 cal g^(-1) .^(@)C^(-1)`.
View SolutionA volume of `10m^(3)` of a liquid is supplied with `100 kal` of heat and expands at a constant pressure of `10 atm` to a final volume of `10.2m^(3)`. Calculate the work done and change in internal energy.
View SolutionThe internal energy of a monatomic ideal gas is `1.5 nRT`.One mole of helium is kept in a cylinder of cross section `8.5 cm^(2)`. The cylinder is closed by a light frictionless piston. The gas is heated slowly in a process during which a total of `42J` heat is given to the gas. If the temperature rise through `2^(@)C`, find the distance moved by the piston. atmospheric pressure `=100 kPa.`
View SolutionCalculate the difference between two specific heats of 1 g of nitrogen. Given molecular weight of nitrogen = 28 and `J = 4.2 times 10^7 erg cal^-1`.
View SolutionCalculate the gas constant for 1 g of gas from the following data :
`C_p=0.245 "cal g"^(-1).^@C^(-1), C_v=0.165" cal g"^(-1).^@C^(-1)and J=4.2 xx10^7 erg cal^(-1)`
View SolutionCalculate difference in specific heats for `1` gram of air at `N.T.P`. Given density of air at N.T.P. is `1.293 g litre^(-1), j=4.2xx10^(7)" erg "cal^(-1)`.
View SolutionCalculate the ratio of specific heats for nitrogen. Given that the specific heat of nitrogen at cinstant pressure `=0.236` cal `g^(-1) K^(-1)` and density at S.T.P. is `0.001234 g//c c`. Atmospheric pressure`=1.01xx10^(6) dyn e//cm^(2)` .
View SolutionFor hydrogen gas, `C_p= 3.409 cal g^-1 ^circC^-1`, `C_V=2.409 cal g^-1 ^circC^-1` and molecular weigh of hydrogen = 2. Calculate the value of J.
View SolutionThe specific heat of argon at constant pressure is 0.127 and ratio of specific hats is 1.667. Calculate the value of J. One litre of argon weighs 1.786 g at N.T.P.
View SolutionTwo moles of oxygen is heated at a constant pressure from `0^(@)C`. What must be the gas for the volume to be doubled ? The specific heat of oxygen under these condition is `0.218 cal g^(-1) K^(-1)` .
View SolutionA certain gas at atmospheric pressure is compressed adiabatically so that its volume becomes half of its original volume. Calculate the resulting pressure in `Nm^(-2)` . Given `gamma` for air = 1.4.
View SolutionA gas is suddenly compressed to `1/4th` of its original volume. Caculate the rise in temperature when original temperature is `27^(@)C. gamma= 1.5`.
View SolutionA tyre pumped to a pressure of 6 atmosphere, suddenly bursts. Room temperature is `15^circ C`. Calculate the temperature of escaping air `gamma= 1.4`.
View Solution`200 cm^(3)` of a gas is compressed to `100cm^(3)` at atmospheric pressure `(10^(6) "dyne"//cm^(2))`. Find the resultant pressure if the change is (i) slow (ii) sudden Take `gamma= 1.4`.
View SolutionA quantity of air at `27^(@)C` and atmospheric pressure is suddenly compressed to half its original volume. Find the final (i) pressure and (ii) temperature.
Given `gamma for air = 1.42`.
View SolutionA quantity of air at normal temperature is compressed (a) slowly (b) suddenly to one third of its volume. Find the rise in temperature, if any in each case, `gamma= 1.4`.
View SolutionA quantity of air is kept in a container having walls which are slightly conducting. The initial temperature and volume are `27^0C` (equal to the temperature of the surrounding) and `800cm^(3)` respectively. Find the rise in the temperature of the gas is compressed to `200 cm^(3)` (a) in a short time (b) in a long time . Take gamma= `1.4`.
View SolutionDry air at 10 atm pressure and `15^circ C` is suddenly compressed to compressed to atmospheric pressure. Find the new temperature. Given `gamma=1.41`, `log 2.88= 0.4594`, `log 1.474=0.1686`.
View SolutionCalculate the rise in temperature when a gas, for which `gamma = 1.5` is compressed to 27 times its original pressure, assuming the initial temperature to be `27^(@)C`.
View Solution`1000 cm^3` of argon at `27^circC` is adiabattically compressed so that the temperature is `127^circC`. Calculate the resulting volume. Given `gamma=5/3`.
View SolutionFind the final value of a gram molecule of a gas after an isothermal expansion at `127^(@)C`, if the original volume is `400 c.c` Given amount of work done by a gram molecule of a gas during expansion is `2302.6 "joule", R= 8.3 "joule mole"^(-1)K^(-1)`
View SolutionCalculate work done to compress isothemally 1 g of hydrogen gas at N.T.P to half its initial volume. Find the amount of heat evolved and change in internal energy. Given `R= 8.31 J mol^-1 K-1`.
View SolutionA sample of hydrogen of mass 6 g is allowed to expand isothermally at `27^circC`. Till its volume is doubled: How many moles of `H_2` do we have? Given, R=8.31 J `mol^- K^-1`.
View SolutionA sample of hydrogen of mass `6g` is allowed to expand isothermally at `27^(@)C` till its volume is doubled.
(a) How may moles of hydrogen are there?
(b) What is final temperature of `H_(2)`?
(c ) Caculate work done during expansion.
View SolutionA sample of hydrogen of mass `6g` is allowed to expand isothermally at `27^(@)C` till its volume is doubled.
(a) How may moles of hydrogen are there?
(b) What is final temperature of `H_(2)`?
(c ) Caculate work done during expansion.
View Solution50g of oxygen at NTP is compressed adiabatically to a pressure of 5 atmosphere. The work done on the gas, if `gamma =1.4 and R = 8.31 J mol^(-1)K^(-1)` is
View SolutionEfficiency of an engine is 0.4, when temperature of its sink ( cold body) is 300 K. What id the temperature of the hot body? Find its efficiency, if the temperature of the hot body is kept unchanged, while temperature of the sink (cold body) is lowered by 50 K. Treat it as reversible engine).
View SolutionA Carnot heat engine operates with an efficiency of 50%. If during each cycle it rejects 150 cal to a reserviour of heat at `30^circC` then what is the temperature of the other reservoir.
View SolutionA Carnot heat engine operates with an efficiency of 50%. If during each cycle it rejects 150 cal to a reserviour of heat at `30^circC` then how much work does it carry out per cycle?
View SolutionA reversible engine converts one-sixth of the heat input into work. When the temperature of the sink is reduced by `62^@C` , the efficiency of the engine is doubled. The temperatures of the source and sink are
View SolutionCalculate the difference in efficiencies of Carnot engine working between 400 K and 350 K
View SolutionCalculate the difference in efficiencies of Carnot engine working between 350 K and 300 K.
View SolutionAn engine has been designed to work between sources and sink temperature of `177^circC` and `27^circC` respectively. If the energy input per cycle is 3600 J, then find its efficiency
View SolutionAn engine has been designed to work between sources and sink temperature of `177^circC` and `27^circC` respectively. If the energy input per cycle is 3600 J, then find work done by the engine per cycle.
View SolutionA perfect Carnot engine utilises an ideal gas as the working substance. The source temperature is `227^circC` and the sink temperature is `127^circC`. Find the efficiency of the engine, and find the heat received from the source and the heat released to the sink when 10,000 J of external work is done.
View SolutionA Carnot engine takes in heat from a reservoir of heat at `427^circC` and gives out heat to sink at `77^circC`. How many clories per second must it take from the reservoir in order to produce useful mechanical work at the rate of 357 W?
View SolutionTwo carnot engines A and B are operated in series. The first one A receives heat at `900K` and rejects it to a reservoir at `T K`. The second engine B receives the heat rejected by the first engine and rejects it to a heat reservoir at `400K`. Calculate the value of `T`, when the efficiency ot two engines is the same.
View SolutionTwo carnot engines A and B are operated in series. The first one A receives heat at `900K` and rejects it to a reservoir at `T K`. The second engine B receives the heat rejected by the first engine and rejects it to a heat reservoir at `400K`. Calculate the value of `T`, when the efficiency ot two engines is the same.
View SolutionRefrigerator A works between `-10^@C` and `27^@C`, while refrigerator B works between `-27^@C` and `17^@C`, both removing heat equal to 2000J from the freezer. Which of the two is the better refrigerator?
View SolutionAssuming that a domestic refrigerator can be regarded as a reversivle engine working between the temperature of melting ice and that of the atmosphere `(170^(@)C)`, calculate the energy which muct be supplied to freeze one kilogram of water already at `0^(@)C`.
View SolutionA refrigerator, whose coefficient performance `beta` is 5, extracts heat from the collingcompartment at the rate of 250 J per cycle.
(a) How much work per cycle is required to operate the refrigerator?
(b) How much heat per cycle is discharges the room which acts as the high temperature reservoir?
View SolutionA refrigerator has to transfer an average of 263J of heat per second from temperature `-10^@C` to `25^@C`. Calculate the average power consumed, assuming no enegy losses in the process.
View SolutionA refrigerator freezes 5 kg of water at `0^(@)C` into ice at `0^(@)C` in a time internal of 20 minutes. Assume that the room temperature is `20^(@)C`. Calculate the minimum power needed to accomplish it.
View SolutionWhat is the change in the internal energy of a system over one complete cycle of a cyclic process?
View SolutionState the first law of thermodynamics.
View SolutionThe internal energy of an ideal gas depends upon
View SolutionIs the internal energy of a gas a function of the pressure? Explain.
View SolutionWhich one among a solid, liquid and gas of same mass and at the same temp. has the greatest internal energy? Which one least? Why?
View SolutionWhen is the heat supplied to a system equal to the increase in its internal energy?
View SolutionA gas does work during isothermal expansion. What is the source of mechanical energy so produced?
View SolutionA gas does work during isothermal expansion. What is the source of mechanical energy so produced?
View SolutionThe temperature of a gas rises during an adiabatic compression, although no heat is given to the gas from outside. Why?
View SolutionAn ideal gas is compressed at a constant temperature, will its internal energy increase or decrease?
View SolutionCooling is produced when a gas at high pressure suddenly expands. Why?
View SolutionWhen a gas is suddenly compressed, its temperature rises. Why?
View SolutionWhen a tyre bursts, the air coming out is cooler than the surrounding air.Explain.
View SolutionIs it possible that there is change in temperature of a body without giving `//` taking heat to from it ?
View SolutionIs it possible that there is change in temperature of a body without giving//taking heat to//from it?
View SolutionCan the temperature of a gas increased keeping its pressure and volume constant ?
View SolutionAir pressure in a car tyre increase during. Explain.
View SolutionWhich molecules, ice at `10^(@)C` or water at `0^(@)C` have greater potential energy and why?
View SolutionA device that converts electric energy into mechanical energy.
View SolutionDuring a process, the volume of a gas is found to depend inversely on the square of its absolute temperature. Find how its pressure will depend on the absolute temperature.
View SolutionLinear expansion is the change in ___________when object is heated or cooled.
View SolutionWhen air of the atmosphere rises up, it cools. Why?
View SolutionIs the equation `PV=RT` valid for both, isothermal and adiabatic changes?
View SolutionIs the equation `PV = RT` valid for both the isothermal and adiabatic changes?
View SolutionFirst law of thermodynamics does not forbid flow of heat from lower teperature to higher temperature. Comment.
View SolutionCan two isothermal curves intersect each other?
View SolutionWhat is the significance of area of closed curve on P-V diagrams?
View SolutionCan the work done during a cyclic process be zero?
View SolutionHow many specific heat does a gas passes?
View SolutionA gas has more than one specific heats, whereas a liquid and solid have only one. Why?
OR
Why gas has two principle specific heat capacties.
View SolutionCompare the formula `C_p - C_v = R` for an ideal gas with the thermodynamics relation `Delta U = Delta Q - P Delta V`.
View SolutionDefine two principal specific heats of a gas. Which is greater and why?
View SolutionWhat is the physical signficance of the difference of two principal specific heat of a gas?
View SolutionCan specific heat of a gas be negative?
View SolutionWhat is specific heat of a gas is an isothermal process?
View SolutionWhat is specific heat of a gas is an adiabatic process?
View SolutionBy what method can the internal energy of an ideal gas be changed?
View SolutionHeat equivalent to 50 joule is supplied to a thermodynamic system and 10 joule work is done on the system. What is the change in the internal energy of the system in the process ?
View Solution400 J of work is done on a gas to reduce its volume by compression adiabatically. What is the change in internal energy of the gas?
View SolutionAn ideal monoatomic gas is taken round the cycle ABCDA as shown in the P-V diagram. The work done during the cycle is
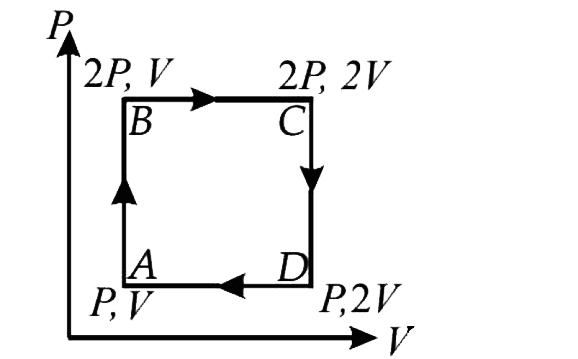
View SolutionWhat is the difference between heat and temperature ?
View SolutionWhy is conversion of heat into work not possible without a sink at lower temperature?
View SolutionExplain why a Carnot engine cannot have 100% efficiency?
View SolutionWhy can a ship not use the internal energy of sea water to operate its engine?
View SolutionIn a Carnot engine, the temperature of the sink is increased. What will happen to its efficiency?
View SolutionWhat is meant by reversible engine? Explain, why the efficiency of a reversible engine is maximum.
View SolutionThe temperature of the surface of the sun is approximately 6000 K. If we take a big lens and focus the sun rays, can we produce a temperature of 8000 K?
View SolutionIs the efficiency of a heat engine more in hilly areas than in plains?
View SolutionIs it theoretically possible to device a heat engine which will create no thermal pollution ?
View SolutionCan a kitchen be cooled by leaving the door of an electric refrigerator open?
View SolutionMilk is poured into a cup of tea and is mixed with a spoon. Is this an example of a reversible process ? Give reason.
View SolutionA system goes from state A to B via two processes I and II, as shown in Fig. 12.25, How are `delta mu_1` and `delta mu_2` (the changes in internal energies in the processes I and II) related to each other ?
View SolutionA thermos flask contains coffee. It is vigorously sheken, considering the coffee as the system. (a) Does its temperature rise ? (b) Has heat been added to it ? (c ) Has work been done on it ?
View Solution
Exercise questions and complete solutions for chapter THERMODYNAMICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11