Complete Solutions to Example of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
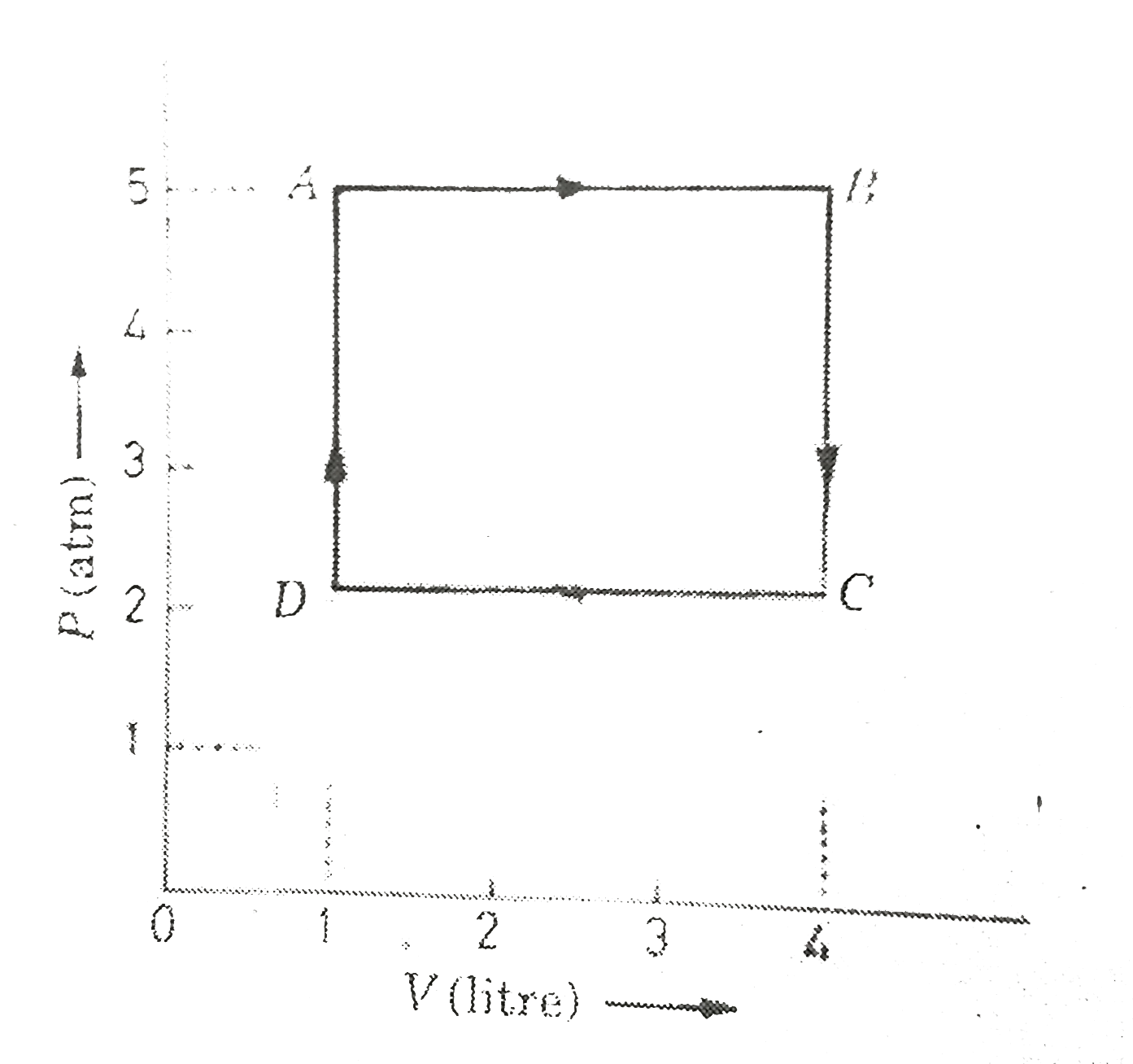
One mole of an ideal gas undergoes a cyclic change ABCD. From the given diagram calculate the net work done in the process.
View SolutionThe `P-V` diagram for a cyclic process is a triangle ABC drawn in order (figure). The co-ordinates of A,B,C are `(4,1), (2,4) and (2,1)` respectively. The co-ordinates are in the order `(P,V)` Pressure is in `Nm^(-2)` and volume is in liter. Calculate work done during the process from A to B, B to C and C to A. Also, calculate work done in the complete cycle.
View Solution1g of water at `100^(@)C` is converted into steam at the same temperature. If the volume of steam is 1671 `cm^(3)`, find the change in the internal energy of the system. Latent of steam `=2256 Jg^(-1)`. Given 1 atmospheric pressure =`1.013xx10^(5) Nm^(-2)`
View SolutionThe volume of steam produced by `1g` of water at `100^(@)C` is `1650 cm^(3)`. Calculate the change in internal energy during the change of state. Given `J= 4.2xx10^(7) erg`.
`cal.^(-1), d= 981 cm^(s-2)`. Latent heat of stream `= 540 cal. G^(-1)`
View Solution`1.0 m^(3)` of water is converted into `1671 m^(3)` of steam at atmospheric pressure and `100^(@)C` temperature. The latent heat of vaporisation of water is `2.3xx10^(6) J kg^(-1)`. If 2.0 kg of water be converted into steam at atmospheric pressure and `100^(@)C` temperature, then how much will be the increases in its internal energy? Density of water `1.0xx10^(3) kg m^(-3)`, atmospheric pressure =`1.01xx10^(5) Nm^(-2)`.
View SolutionAt `0^(@)C` and normal atmospheric pressure, the volume of 1 gram of water increases from `1 c.c "to" 1.091 c.c` on freezing. What will be the change in its internal energy? Normal atmospheric pressure is `1.013xx10^(5)N//m^(2)` and latent heat of melting of ice `= 80 cal//gram`.
View Solution5 mole of oxygen are heated at constant volume from `10^(@)C "to" 20^(@)C`. What will be the change in internal energy of the gas? Gram molar specific heat of gas at constant pressure `=8cal. "Mole"^(-1).^(@)C^(-1)` and `R=8.36J "mole"^(-1).^(@)C^(-1)`.
View SolutionIf 70 cal of heat is required to raise the temperature of moles of an ideal gas at constant pressure from `30^(@)C` to `35^(@)C`, calculate (i) the work done by the gas (ii) the increases in internal energy of the gas and (iii) degrees of freedom of gas molecules. given `R =2 cal mol ^(-1) K^(-1)`
View SolutionA cyclinder with a movable piston contains `3 mol s` of hydrogen at standard temperature and pressure. The walls of the cyclinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increases, if the gas is compressed to half its original volume? Given `gamma= 1.4`.
View SolutionThe compression ratio of a certain diesel engine is 15. this means that air the cylinder is compressed to 1/15 of its initial volume. If the initial pressure is `1.0xx10^(5)` Pa and the initial temperature is 300 K, find the final pressure and temperature after compression. air is mostly a mixture of oxygen and nitrogen and `gamma=1.4`
View SolutionIf at `50^(@)C` and `75 cm` of mercury pressure, a definite mass of gas is compressed (i) slowly (ii) suddenly, than what will be the final pressure and temp. of the gas in each case, if the final volume is one fourth of the initial volume? `gamma= 1.5`.
View SolutionA tyre pumped to a pressure `3.375 atm "at" 27^(@)C` suddenly bursts. What is the final temperature `(gamma = 1.5)`?
View SolutionA gas occupying one litre at 80 cm pressure is expanded adiabatically to `1190 cm^(3)`. If the pressure falls to 60 cm in the process, deduce the value of `gamma`.
View SolutionTen litres of air at `17^(@)C` and 76 cm of Hg pressure is compressed adiabatically to a volume of 0.5 litre. Calculate the final temperature and pressure attained. Given `gamma=1.41`
View SolutionCalculate the fall in temperature of helium initially at `15^(@)C`, when it is suddenly expanded to `8 times` its original volume `(gamma=5//3)`.
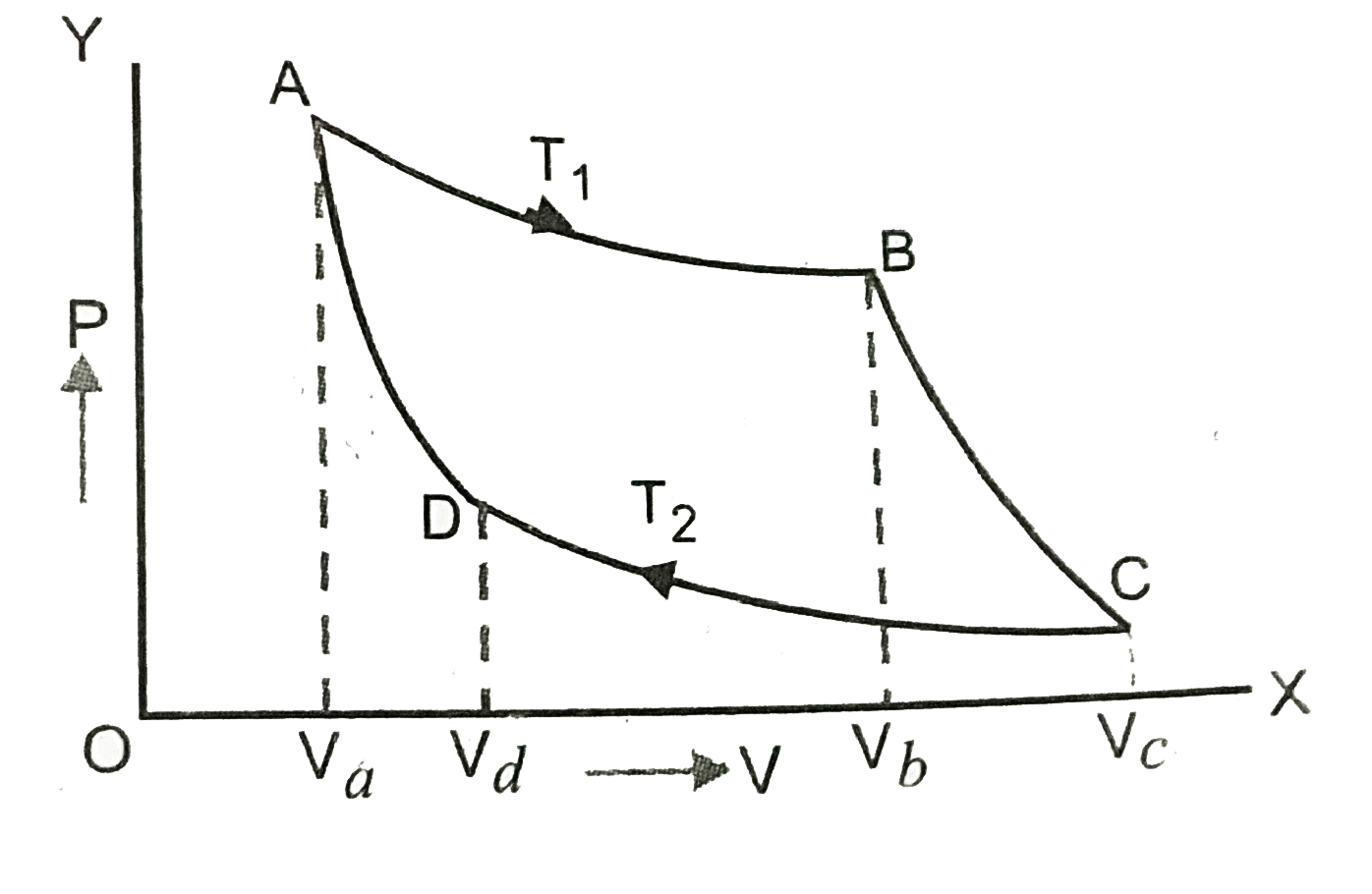
View SolutionTwo different adiabatic curves for the same gas intersect two isothermals at `T_(1), and T_(2)` as shown in `P-V` diagram, (figure). How does the ratio `(V_(a)//V_(d))` compare with the ratio `(V_(b)//V_(c))` ?
View SolutionTwo sample `A` and `B` of a gas initially at the same pressure and temperature are compressed from volume `V` to `V//2` (A isothermally and `B` adiabatically). The final pressure of `A` is
View SolutionA sound wave passing through air at `NTP` produces a pressure of `0.001 "dyne"/cm^(2)` during a compression. The corresponding change in temperature (given `gamma = 1.5` and assume gas to be ideal) is
View SolutionThree moles of an ideal gas kept at a constant temperature of `300K` are compressed from a volume of 4 litre to 1 litre. Calculate work done in the process. `R= 8.31 J mol e^(-1)K^(-1)`.
View SolutionA gram molecule of a gas at `127^(@)C` expands isothermally until its volume is doubled. Find the amount of work done and heat absorbed.
View SolutionA cylinder containing one gram molecule of the gas was compressed adiabaticaly untill its tempertaure rose from `27^(@)C` to `97^(@)C`. Calculate the work done and heat produced in the gas `(gamma=1.5)`.
View Solution`1 g` mole of an ideal gas at STP is subjected to a reversible adiabatic expansion to double its volume. Find the change in internal energy `( gamma = 1.4)`
View SolutionFind the work required to compress adiabatically 1 gram of air initially at N.T.P. to half its volume. Density of air at N.T.P. =0.00129 g `cm^(-3)` and `gamma=1.4`
View SolutionOne mole of a perfect gas, initally at a pressure and temperature of `10^(5) N//m^(2)` and 300 K, respectively, expands isothermally unitl its volume is doubled and then adiabatically until its volume is again doubled. Find final pressure and temperature of the gas Find the total work done during the isothermal and adiabatic processes. Given `gamma = 1.4`. Also draw the P-V diagram for the process.

View SolutionEfficiency of carnot engine working between ice point and steam point is
View SolutionOne of the most efficient engines ever developed operated between 2100K and 700K. Its actual efficiency is 40%. What percentage of its maximum possible efficiency is this?
View SolutionThe source tempreature of a Carnot engine is `127^(@)C`. It takes 500 cal of heat from the source and rejects 400 cal to the sink during each cycle. What is the temperature of the sink ?
View SolutionIn a heat engine, the temperature of the source and sink are 500 K and 375 K. If the engine consumes `25xx10^5J` per cycle, find(a) the efficiency of the engine, (b) work done per cycle, and (c) heat rejected to the sink per cycle.
View SolutionThe efficiency of a Carnot cycle is `1//6`. If on reducing the temperature of the sink by `65^@C`, the efficiency becomes `1//3`, find the source and sink temperatures between which the cycle is working.
View SolutionA reversible engine converts one fifth of heat which it absorbs from source into work. When the temp. of sink is reduced by `70^(@)C`, its efficiency is doubled. Calculate the temperature of the source and sink.
View SolutionA cornot engine has the same efficiency between (i) 100 K and 500 K and (ii) T and 900 K. Find T.
View SolutionA carnot engine whose heat sink is at `27^(@)C` has an efficiency of `40%`. By how many degrees should the temperature of source be changed to increase the efficiency by `10%` of the original efficiency?
View SolutionThree designs are proposed for an engine which is to operate between 300 K and 500 K. design A is claimed to produced 3000 J of work per kcal of heat input, B is claimed to produced 2000 J and C , 1000 J. which design would you choose ? Given 1 kcal =4185 J
View SolutionAn ideal engine operates by taking in steam from a boiler at `327^(@)C` and rejecting heat to a sink at `27^(@)C`. The engine runs at `500 rpm` and heat taken is `600 k cal` in each revolution. Calculate(i) efficiency of engine (ii) work done in each cycle (iii) heat rejected in each revolution and (iv) power output of engine.
View SolutionDuring isothermal expansion at 800 K, the working substance of a Carnot's engine extracts 480 cal of heat. If the sink be at 300 K, calculate (i) the work done by the working substance during isothermal expansion (ii) the work done on the substance during isothermal compression (iii) the efficiency of the ideal engine.
View SolutionA reversible engine takes in heat from a reservoir of heat at `527^(@)C`, and gives out to the sink at `127^(@)C` How many calories per second must it take from the reservoir in order to produce useful mechanical work at the rate of `750 wat t`? `1 cal. = 4.2J`.
View SolutionAn engine (whose efficiency equals that of a carnot engine working between the same temperature limits) develops 100 h.p. and operates between `227^(@)C` and `27^(@)C`. What is the heat supplied ? What is the heat rejected ? What is the thermal efficiency ?
View SolutionTwo carnot engines A and B are operates in series. The first one A receives heat at 800 K and rejects to a reservoir at temperature TK. The second engine B revives the heat rejected to a heat reservoir at 300 K. calculate the temperature TK for the following cases.
(i) When the outputs of the two engines are equal.
(ii) When the efficiencies of the two engines are equal.
View SolutionA carnot cycle is performed by `1 mol e of air (gamma=1.4)` initially at `327^(@)C`. Each stage represents a compression or expansion in the ratio `1:6`. Calcultate (a) the lowest temperature (b) net work done during each cycle and (C ) efficiency of the engine.
Take `R=8.31J mol e^(-1)K^(-1)`.
View SolutionIn A double -acting steam engine, the avearge pressure of steam is `8xx10^(4) Nm^(-2)`. The length of the stroke is 0.8 m and area of cross-section of the piston is `0.18 m^(2)`. If the piston makes 6 revolution per second, calculate the horse power of the engine.
View SolutionA petrol engine consume 25 kg of petrol per hour. The calorific value of petro lis `11.4xx 10^(6)` cal `kg^(-1)`. The power of the engine is 99.75 kW. Calculate the efficiency of the engine.
View SolutionIn a petrol engine, the rate of production of heat due to combustion of the fuel is `5xx10^(6) cal h^(-1)`. The efficiency of the engine is 30%. Calculate the H.P. of the engine. Given, J=4.2 J `cal^(-1)` and 1 h.p. =746 W.
View SolutionThe efficiency of otto cycle for petrol engine is 50% and the adiabatic constant is 1.4. calculate the compression ratio.
View SolutionHow much heat energy is required to do 10 kWh of work by a petrol engine, whose adiabatic compression ratio is 10 ? Given `gamma=1.4`
View SolutionIn a refrigerator, heat from inside at 277K is transferred to a room at 300K. How many joules of heat shall be delivered to the room for each joule of electrical energy consumed ideally?
View SolutionCalculate the least amount of work that must be done to freeze one gram of wate at `0^@C` by means of a refrigerator. Temperature of surroundings is `27^@C`. How much heat is passed on the surroundings in this process? Latent heat of fusion `L=80cal//g`.
View SolutionHow much energy in watt hour may be required to convert `2kg` of water into ice at `0^(@)C`, assuming that the refrigerator is ideal? Take room temp. `=25^(@)C`, which is also the initial temp. of water and temp. of freezer is `-15^(@)C`.
View SolutionIn a cold storage, ice melts at the rate of `2 kg//h` when the external temperature is `20^(@)C`. Find the minimum power output of the motor used to drive the refrigerator which just prevents the ice from melting. Latent heat of fusion of `ice = 80 cal//g`
View SolutionA carnot engine having a perfect gas aas the working substance is driven backwards and is used for freezing water already at `0^(@)C`. If the engine is driven by `500W` electric motor with an efficiency of `60%` how long will it take to freeze `15kg` of water? The working temps of the engine are `15^(@)C` and `0^(@)C`. The system involves no energy losses. Given latent heat of ice `=333xx10^(3)J kg^(-1)`.
View SolutionHeat is flowing through a rod of length `25.0 cm` having cross-sectional area `8.80 cm^(2)`. The coefficient of thermal conductivity for the material of the rod is `K = 9.2 xx 10^(-2) kcal s^(-1) m^(-1) .^(@)C^(-1)`. The Temperatures of the ends of the rod are `125^(@)C` and `0^(@)C` in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of `10.0 cm` from the hot end and (iii) rate of flow of heat.
View SolutionA thermocole cubical icebox of side 30 cm has a thickness of 5.0 cm if 4.0 kg of ice are put ini the box, estimate the amount of ice remaining after 6 h. The outside temperature is `45^@C` and coefficient of thermal conductivity of thermocole`=0.01 J//kg`.
View SolutionA brass boiler has a base area of `0.15m^2` and thickness 1.0 cm it boils water at the rate of `6.0 kg//min`, When placed on a gas. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass`=109 J//s-.^@C` ) and heat of vapourization of water `=2256 J//g`.
View SolutionSteam at `100^(@)C` is passed into a copper cylinder 10 mm thick and of `200 cm^(2)` area. Water at `100^(@)C` collects at the rate of `150 g min^(-1)`. Find the temperature of the outer surface, if the conductivity of copper is `0.8 cal s^(-1) cm^(-1) .^(@)C^(-1)` and the latent heat of steam is `540 cal g^(-1)`.
View SolutionA metal rod of length 20 cm and diamter 2 cm is convered with a non conducting substance. One of its ends is maintained at `100^(@)C` , while the other end is put at `0^(@)C`. It is found that 25 g ice melts in 5 min. calculate the coefficient of thermal conductivity of the metal. Latent that of ice = `80 cal g^(-1)`.
View SolutionA layer of ice 2 cm thick is formed on a pond. The temperature of air is `-20^(@)C`. Calculate how long it will take for the thickness of ice to increase by 1mm. Density of ice `= 1g cm^(-3)`. Latent heat of ice `= 80 cal g^(-1)`. Conductivity of ice `= 0.008 cal s^(-1) cm^(-1) .^(@)C^(-1)`.
View SolutionTwo vessels of different materials are identical in size and wall-thickness. They are filled with equal quantities of ice at `0^(@)C`. If the ice melts completely in 10 and 25 minutes respectively, compare the coefficients of thermal conductivity of the materials of the vessels.
View SolutionTwo vessels A and B of different materials but having identical shape, size and wall-thickness are filled with ice and kep at the same plane. Ice melts at the rate of `100 g min^(-1)` and `150 g min^(-1)` in A and B respectively. Assuming that heat enters the vessels through the walls only, calculate the ratio of thermal conductivity of their materials.
View SolutionTwo plates of equal areas are placed in contact wih each other. Their thickness are 2.0 cm and 5.0 cm respectively. The temperature of the external surface of the first plate is `-20^(@)C` and that of the external surface of the second plate is `20^(@)C`. What will be the temperature of the current surface if the plates (i) are of the same material, (ii) have thermal conductivities in the ratio `2:5`.
View SolutionThree bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of `2:4:3`. If the open ends of the first and the last bars are at temperature `200^(@)C` and `180^(@)C` respectivity in the steady state, calculate the temperature of both the junctions.
View SolutionHeat is supplied to a slab of cork, 5cm thick and of `2m^(2)` by a heating coil spread over its surface. When the current in the coil is 1.18 A and the potential difference across its end is 20 V, the steady temperatures of the faces of the slab are `12.5^(@)C` and `0^(@)C`. Assuming that the whole of the heat developed in the coil is conducted through the slab, calculate the thermal conductivity of the cork.
View SolutionWhat is the temperature of the steel-copper junction in the steady state system show in Fig. `7(e).17`? Length of steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace `=300^(@)C`, temperature of other end `0^(@)C`. The are of cross-section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel `=50.2 js^(-1) m^(-1) K^(-1)` and of copper `=3895 js^(-1) m^(-1) K^(-1)`).

View SolutionThe surface temperature of a hot body is `1227^(@)C`. Find the wavelength at which it radiates maximum energy. Given Wien's constant `= 2898 cm K`.
View SolutionTwo stars radiate maximum energy at wavelength `3.6 xx 10^(-7)m` and `4.8 xx 10^(-7) m` respectively. What is the ratio of their temperature?
View SolutionThe spectral energy distribution of the sun has a maximum at `4754Å`. If the temperature of the sun is 6050 K, what is the temperature of a star for which this maximum is at `9506Å`?
View SolutionCalculate the temperature (in K) at which a perfect black body radiates energy at the rate of `5.67W cm^(-2)`. Given `sigma = 5.67 xx 10^(8)Wm^(-2)K^(-4)`.
View SolutionLuminosity of Rigel star in Orion constellation is 17, 000 times that of our sun. If the surface temperature of the sun is 6000 K, calculate the temperature of the star.
View SolutionA small hole is made in a hollow sphere whose walls are at `723^(@)C`. Find the total energy radiated per seond per `cm^(2)`. Given Stenfan's constant `= 5.7 xx 10^(-5) erg cm^(-2) s^(-1) K^(-4)`.
View SolutionConsider the sun to be a perfect sphere of radius `6.8 xx 10^(8)m`. Calculate the energy radiated by sun in one minute. Surface temperature of the sun `= 6200 K`. Stefan's constant `= 5.67 xx 10^(-8) J m^(-2) s^(-1) K^(-4)`.
View SolutionHow much energy in radiated per minute from the filament of an incandescent lamp at 3000 K, if the surface area is `10^(-4)m^(2)` and its emissivity is `0.4`? Stefan's constant `sigma = 5.67 xx 10^(-8) Wm^(-2)K^(-4)`.
View SolutionAt what temperature will the filament of 100 W lamp operate if it is supposed to be perfectly black of area `1 cm^(2)`.
Given `sigma = 5.67 xx 10^(-5) erg cm^(-2) s^(-1) K^(-4)`.
View SolutionDue to change in main voltage, the temperature of an electric bulb rises from 3000K to 4000K. What is the percentage rise in electric power consumed?
View SolutionThe ratio of radiant energies radiated per unit surface area by two bodies is `16 : 1`, the temperature of hotter body is 1000 K , then the temperature of colder body will be
View SolutionA black body at `27^(@)C` surrounds another black body at `-73^(@)C`. Calculate the net heat transfer per second per square meter of the body at higher temperature..
View SolutionAn indirectly heated filament is radiating maximum energy of wavelength `2.16xx10^-5cm`. Find the net amount of heat energy lost per second per unit area, the temperature of the surrounding air is `13^@C`. Given `b=0.288cm-K.sigma=5.77xx10^-5erg//s-cm^(2)-K^(4)`).
View SolutionCalculate the maximum amount of heat which may be lost per second by radiation by a sphere 14cm in diameter at a temperature of `227^(@)C`, when placed in an enclosure at `27^(@)C`. Given Stefan's constant =`5.7 xx 10^(-8)Wm^(-2)K^(-4)`.
View SolutionTwo bodies A and B are kept in evacuated vessels maintained at a temperature of `27^(@)C`. The temperature of A is `527^(@)C` and that of B is `127^(@)C`. Compare the rates at which heat is lost from A and B.
View SolutionHow much faster does a cup of coffee cool off from `100^(@)C` than from `30^(@)C`? Assume the coffee to act as a black body and temp. of surrounding = `20^(@)C`.
View SolutionA liquid takes 5 minutes to cool from `80^@C` to` 50^@C` . How much time will it take to cool from `60^@C` to `30^@C`? The temperature of surroundings is `20^@C`.
View SolutionA body cools in 7 minutes from `60^(@)C` to `40^(@)C`. What will be its temperature after the next 7 minutes? The temperature of the surrounding is `10^(@)C`. Assume that Newton's law of cooling holds good throughout the process.
View SolutionDefine the term thermodynamics.
View SolutionDefine the terms thermodynamic system, surroundings, thermodynamic variable and equation of state.
View SolutionDefine thermal equilibrium. How is it attained?
View SolutionWhat is an indicator diagram? What is its importance?
View SolutionDescribe an analytical method for determining the work done during the expansion of gas.
View SolutionWhat is non-cyclic process? Show that the area under the P-V diagram gives the work done by a system in a non-cyclic process.
View SolutionWhat is cyclic process? Prove that the net work done durng a cyclic process is numerically equal to the area of the loop representing the cycle.
View SolutionOne mole of an ideal gas undergoes a cyclic change ABCD. From the given diagram calculate the net work done in the process.

View SolutionOne mole of an ideal gas undergoes a cyclic change ABCD where the (P,V) co-ordinates are A (5,1), B (5,3), C (2,3) and D (2,1). P is atmosphere and V is in litre. Calculate work done along AB, BC, CD and DA and also net work done in the process. Given `1 atmosphere = 1.01 times 10^5 Nm^-2`.
View SolutionState and explain first law of thermodynamics. Discuss the application of first law of thermodynamics to (i) isothermal process, (ii) adiabatic process.
View Solution1g of water at `100^(@)C` is converted into steam at the same temperature. If the volume of steam is 1671 `cm^(3)`, find the change in the internal energy of the system. Latent of steam `=2256 Jg^(-1)`. Given 1 atmospheric pressure =`1.013xx10^(5) Nm^(-2)`
View SolutionThe volume of steam produced by `1g` of water at `100^(@)C` is `1650 cm^(3)`. Calculate the change in internal energy during the change of state. Given `J= 4.2xx10^(7) erg`.
`cal.^(-1), d= 981 cm^(s-2)`. Latent heat of stream `= 540 cal. G^(-1)`
View Solution`1.0 m^(3)` of water is converted into `1671 m^(3)` of steam at atmospheric pressure and `100^(@)C` temperature. The latent heat of vaporisation of water is `2.3xx10^(6) J kg^(-1)`. If 2.0 kg of water be converted into steam at atmospheric pressure and `100^(@)C` temperature, then how much will be the increases in its internal energy? Density of water `1.0xx10^(3) kg m^(-3)`, atmospheric pressure =`1.01xx10^(5) Nm^(-2)`.
View SolutionAt `0^(@)C` and normal atmospheric pressure, the volume of 1 gram of water increases from `1 c.c "to" 1.091 c.c` on freezing. What will be the change in its internal energy? Normal atmospheric pressure is `1.013xx10^(5)N//m^(2)` and latent heat of melting of ice `= 80 cal//gram`.
View Solution5 mole of oxygen are heated at constant volume from `10^(@)C "to" 20^(@)C`. What will be the change in internal energy of the gas? Gram molar specific heat of gas at constant pressure `=8cal. "Mole"^(-1).^(@)C^(-1)` and `R=8.36J "mole"^(-1).^(@)C^(-1)`.
View SolutionA metal of mass 1 kg at constant atmospheric pressure and at initial temperature `20^@C` is given a heat of 20000J. Find the following
(a) change in temperature,
(b) work done and
(c) change in internal energy.
(Given, specific heat `=400J//kg-^@C`, cofficient of cubical expansion, `gamma=9xx10^-5//^@C`, density `rho=9000kg//m^3`, atmospheric pressure `=10^5N//m^2`)
View SolutionThe efficiency of a Carnot engine operating between temperatures of `100^(@)C` and `-23^(@)C` will be
View SolutionDefine the two principle specific heats of a gas. Explain wy molar specific heat at constant pressure `(C_p)` is greater than the molar specific hat at constant comlume `(C_V)` ?
View SolutionApplying the first law of thermodynamics, obtain the relation between the two specific hats of a gas.
View SolutionCalculate the specific heat capacity at constant volume for a gas. Given specific heat capacity at constant pressure is `6.85 cal mol^(-1) K^(-1), R = 8.31 J mol^(-1)K^(-1)`.
`J = 4.18 J cal^(-1)`.
View SolutionCalculate the difference between the two principal specific heats of 1g of helium gas at S.T.P. Given atomic weight of helium = 4 and `J = 4.186 J cal^(-1)` and `R = 8.31 J mol^(-1)K^(-1)`.
View Solution
Example questions and complete solutions for chapter THERMODYNAMICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11