Complete Solutions to Problem of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| SL ARORA | Problem |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
A force of 6.4 N stretches a vertical spring by 0.1m. Find the mass that must be suspended from the spring so that it oscillates with a period of `pi//4`
second.
View SolutionTwo simple harmonic motions are represented by the equations.
`x_(1)=5sin(2pit+(pi)/(4)),x_(2)=5sqrt(2)(sin2pit+cos2pit)`
find the ratio of their amplitudes.
View SolutionThe simple harmonic motions are represented by the equations:
`y_(1)=10sin((pi)/(4))(12t+1), y_(2)=5(sin3pit+sqrt(3)))`
View SolutionA point particle of mass 0.1 kg is executing SHM of amplitude 0.1m. When the particle passes through the mean position, its kinetic energy is `8xx10^(-3)J`. Obtain the equation of motion of the particle if the initial phase of oscillation is `45^(@)`
View SolutionA simple harmonic motion has an amplitude A and time period T. What is the time taken to travel from `x=A` to `x=A//2`?
View SolutionA particle executes SHM of period 1.2 s and amplitude 8 cm. find the time it takes to travel 3 cm the positive extremity of its oscillation. Given `cos^(-1)(0.625)=51^(@)`.
View SolutionA block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and pisto separate? What is the maximum velocity of the piston at this amplitude?
View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface `g=10ms^(-1)`
View SolutionTwo linear harmonic motions of equal amplitudes and frequencies `omega` and 2 `omega` imposed on a particle along the axes of x and y respectively. If the initial phase difference between them is `pi//2`, then find the resultant path followed by the particle.
View SolutionTwo particles execute simple harmonic motion of same amplitude and frequency along the same straight line. They pass on another, when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
View SolutionA silver atom in a solid oscillates in SHM in a certain direction with a frequency of `10^(12)s^(-1)`. What is the force constant of the bonds connecting one atom with the other? Molecular weight of silver 108 and avogadro number `=6.02xx10^(23)gmol^(-1)`
View SolutionSprings of apring constants `k,2k,4k,8k` . . . Are connected in series. A mass m kg is attached to the lower end of the last spring and the system is allowed to vibrate. What is the time period of oscillations?
View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths `l_(1)` and `l_(2)`, where `l_(1)=nl_(2)` and n is an integer. What are the corresponding force constant `k_(1)` and `k_(2)` in terms of n and k? what is the ratio `k_(1)//k_(2)`
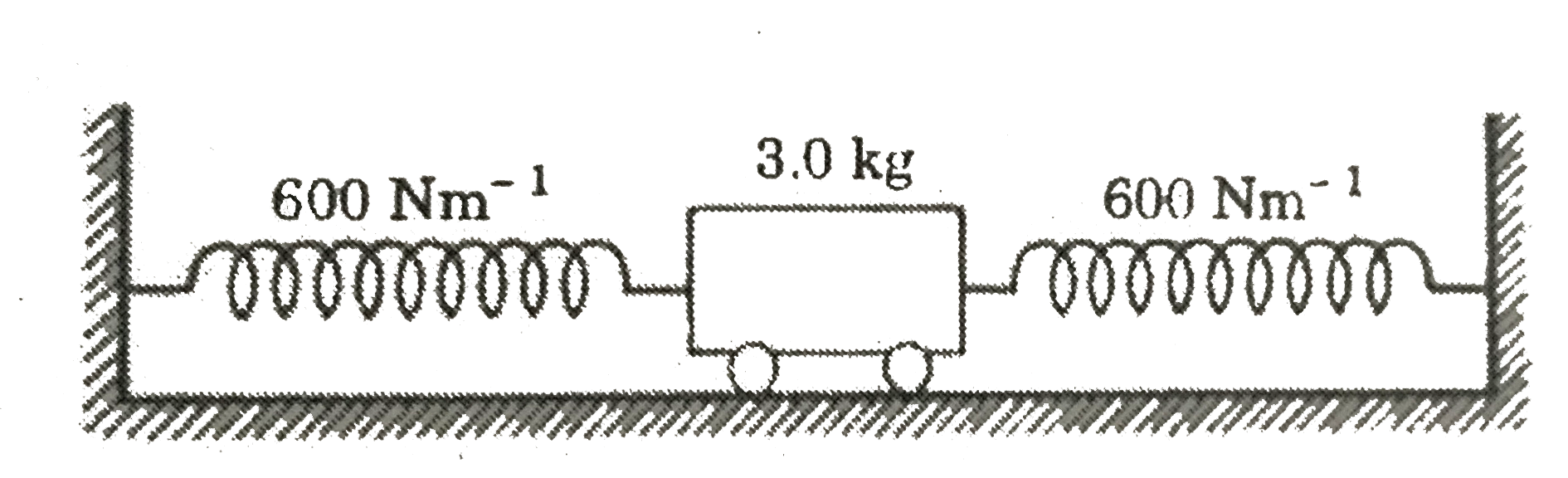
View SolutionA body of mass 1.0 kg is suspended from a weightless spring having force constant `600Nm^(-1)`. Another body of mass 0.5 kg moving vertically upwards hits the suspended body with a velocity of `3.0ms^(-1)` and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
View SolutionA horizontal spring block system of mass M executes simple har monic motion.w hen the block is passingle through its equilibrium position, an object of mass m is put on it and the two move tother. Find the new amplitude and frequency of vibration.
View SolutionA certain spring stretches 25 cm when a 500 g mass is hung from its end. It is now used as shown in fig. With 2 kg mass at one end placed on a frictionless surface. Suppose the mass is pulled to the right until the spring is stretched to 10 cm and then released. find the speed with which the mass moves through the unstretched position.
View SolutionTwo bodies of masses 1 kg and 3 kg respectively are connected rigidly by a vertcal spring. The body of mass 3 kg rests on a smototh horizontal surface. The force constant of the spring is `484Nm^(-1)`. From the equilibrium position, the mass of 1 kg is displaced vertically through a distance of 0.02 m and then released. calculate (i) and frequency of oscillation of the mass of 1 kg (ii) the maximum velocity of this mass (iii) its oscillation energy and (iv) the reaction of the table on the mass of 3 kg, when mass 1 kg is having harmonic oscillations.
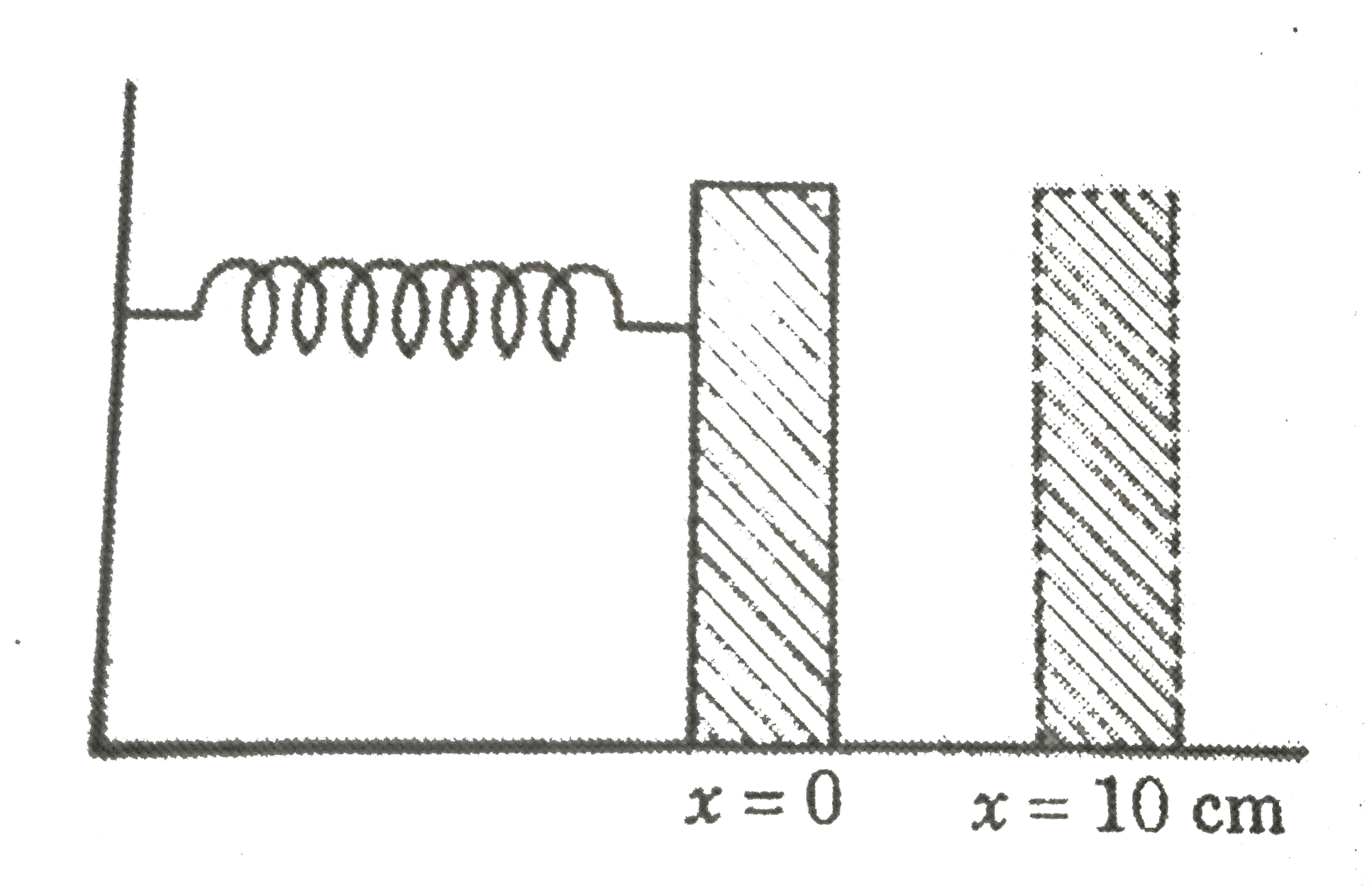
View SolutionThe bob of pendulum of length l is pulled aside from its equilibrium position through an angle `theta` and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionA simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionTwo identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length `zof0.06 pi` meter and spring spring constant5 `0.1 N//m`. Initially, both the balls are displaced by an angle `theta = pi// 6` radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.
View SolutionA thin rod of length (L) and area of cross - section (S) is pivoted at its lowest point (P) inside a stationary, homegeneous and non - viscous liquid. The rod is free to ratate in a vertical plane about a horizontal axis passing through (P). The density (d_1) of the material of the rod is smaller than the density (d_2) of the liquid. The rod is displaced by a small angle (theta) from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
 .
.
View Solution
Problem questions and complete solutions for chapter OSCILLATIONS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11