Complete Solutions to Problems for self practice of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| SL ARORA | Problems for self practice |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
A harmonic oscillation is represented by y=0.34 cos (3000t+0.74), where y and t are in mm and s respectively. Deduce (i) and amplitude (ii) the frequency and angular frequency (iii) the period and (iv) the intial phase.
View SolutionWrite the displacement equation representing the following conditions obtained for a simple harmonic motion: amplitude=0.01m, frequency=600Hz initial phase `=pi//6`
View SolutionA simple harmonic oscillation is represented by the equation. `y=0.40sin(440t+0.61)`
Here y and t are in m are s respectively. What are the values of (i) amplitude (ii) angular frequency (iii) frequency of oscillations (iv) time period of oscillations and (v) initial phase?
View SolutionThe periodic time of a body executing SHM is 2s. After how much time interval from t=0, will its displacement be half of its amplitude?
View SolutionA particle executes SHM represented by the equation `10y=01sin50pit,` where the displacement y is in metre and time t in second. Find the amplitude and frequency of the particle.
View SolutionThe motion of a 100 g mass tied to a spring is described by the equation `x=25cos(3t+(pi)/(4))cm`. Find (i) the angular velocity `omega`(ii) frquency v (iii) the time period T (iv) the force constant k (v) the amplitude A and (v) the phase angle
View SolutionThe displacement of a particle excuting periodic motion is given by `y=4cos^(2)(t//2)sin(1000t)`. Find the independent constituent SHM's.
View SolutionThe displacement of a particle executing SHM is given by
`y=0.2sin50pi(t+0.01)`metre
Calculate the amplitude,t he period, maximum velocity and the displacement at the start of the motion.
View SolutionA particle executing SHM completes 1200 oscillations per minute and passes through the mean position with a velocity of `31.4ms^(-1)`. Determine the maximum displacement of the particle from the mean position also obtain the displacement equation of the aprticle if its displacemet be zero at the instant t=0.
View SolutionThe time period of a body executing SHM is 0.05 s. if the amplitude is 4 cm, then what will be the maximum velocity and maximum acceleration of the body?
View SolutionThe maximum velocity of a particle executing SHM is `100cms^(-1)` and the maximum acceleration is `157cms^(-2)` determine the periodic time
View SolutionA body of mass 0.1 kg is executing SHM of amplitude 1.0 m and period 0.2 s. what is 2 cm. find the time period.
View SolutionA particle executing SHM has an acceleration of `0.5cms^(-1)` when its displacement is 2 cm. find the time period.
View SolutionA body executing SHM makes 100 vibrations/min if the speed at the mean position is `15ms^(-1)`, calculate its path length. What is its velocity when it is half way be tween its mean position and extreme position?
View SolutionA particle is executing SHM if `u_(1) and u_(2)` are the speeds of the particle at distances `x_(1) and x_(2)` from the equilibrium position, shown that the frequency of oscillation
`f=(1)/(2pi)((u_(1)^(2)-u_(2)^(2))/(x_(2)^(2)-x_(1)^(2)))`
View SolutionIf a particle executes SHM of time period 4 s and amplitude 2 cm, find its maximum velocity and that at half its full displacement also find the acceleration at the turning points and when the displacement is 0.75 cm
View SolutionShow that if a particle is moving in SHM, its velocity at a distance `sqrt(3)//2` of its amplitude from the central position is half its velocity in central position.
View SolutionA particle executes SHM of period 12 seconds and amplitude 8 cm. Find time it takes to travel 3 cm from the positive extremity of its oscillation.
View SolutionA particle executes SHM of period 12s. Two sec after it passes through the centre of oscillation, the velocity is found to be 3.142 cm `s^(-1)` fin dht amplitude and the length of the path.
View SolutionA particle is moving in a st. line with SHM. Its velocity has the values 3 `ms^(-1)` and `2ms^(-1)` when its distance from the mean positions are 1 m and 2 m respectively find the period of its motion and length of its path.
View SolutionA block lying on a horizontal table executes SHM of period 1 second, horizontally. What is the maximum amplitude for which the block does not slide if coeff. Of friction between block and surface is `0.4, pi^(2)=10. `
View SolutionA horizontal platform moves up and down simple harmonically, the total vertical movement being 10 cm what is the shortest period permissible, if object resting on the platform are to remain in contact with it throughout the motion.? Take `g=980cms^(-2)`
View SolutionIn a gasoline engine, the motion of the piston is simple harmonic. The piston has a mass of 2 kg and stroke (twice the amplitude) of 10 cm. find maximum acceleration and the maximum unbalanced force on the piston, if it is making 50 complete vibrations each minute.
View SolutionA man stands on a weighing machine placed on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of platform is 5cm. Take `g=10ms^(-2)`
View SolutionFrom the figure, obtain the equation of simple harmonic motion of the y-projection of the radius vector of the revolving particle P in each case.
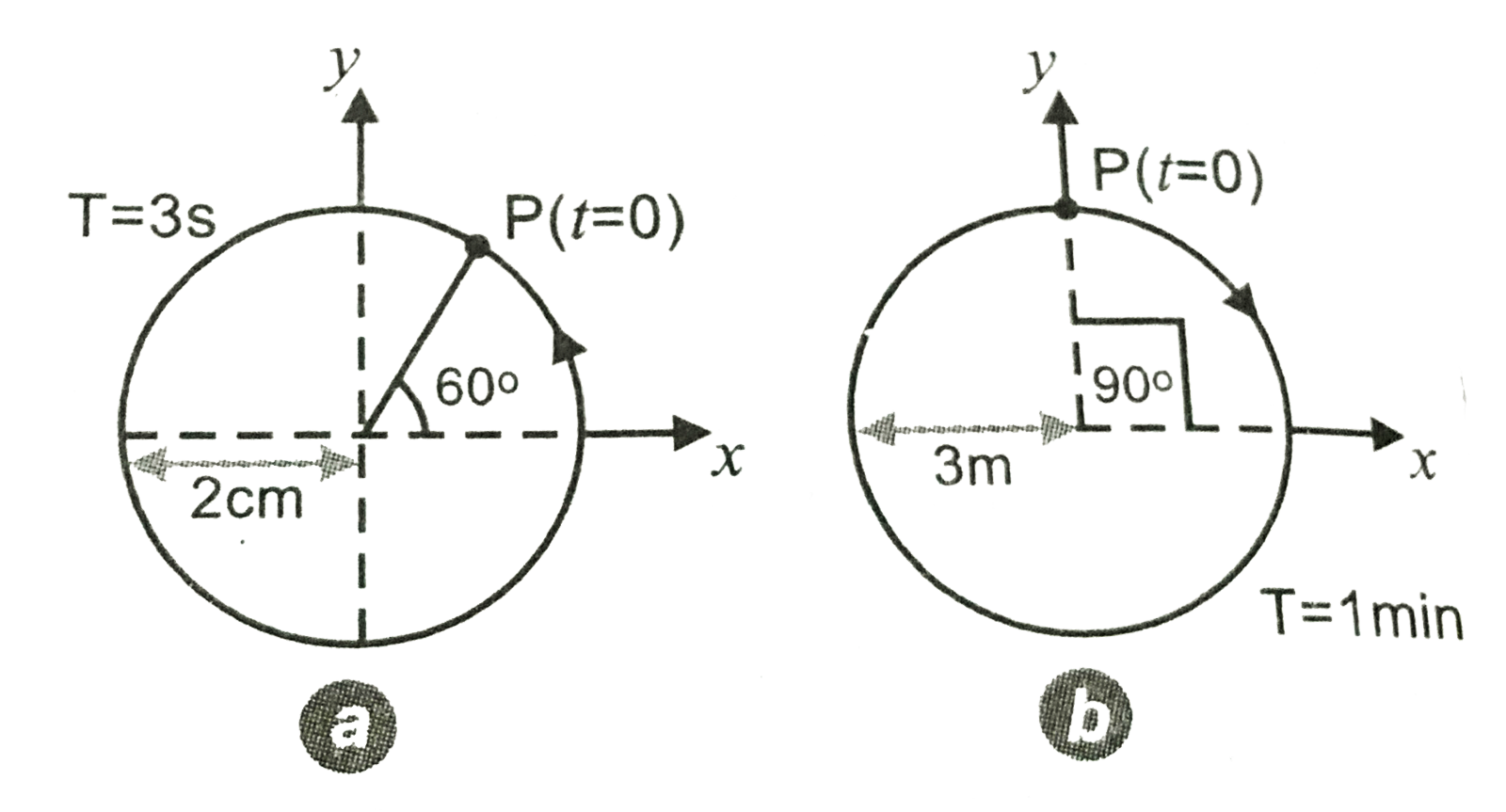
View SolutionIf a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
View SolutionA 20 gram weight produces an extension of 2 cm in a vertical spring. A mass of 100 gram is suspended at its bottom and left pulling down. Calculate the frequency of its vibration.
View SolutionA body of mass 2 kg is made to oscillate using a spring of force constant `8Nm^(-1)` find (i) angular frequency (ii) frequency of vibration (iii) time period of vibration.
View SolutionA spring 60 cm long is stretched 2 cm, when subjected to a force of 20 gram weight what would be the length, when a force of 500 gram weight is applied.?
View SolutionA thin wire is used to support 100 kg weight. The wire stretches by 0.5 mm. Calculate the force constant k (in `Nm^(-1)`) of the wire.
View SolutionAn uncalibrated spring balance is found to have a period of oscillation of 0.314 s, when a 1 kg weight is suspended from it? How dows the spring elongate, when a 1 kg weight is suspended from it? [take `pi=3.14`]
View SolutionA spring compressed by `0.1`m develops a restoring force 10N. A body of mass 4kg is placed on it. Deduce `(i)` the force constant of the spring `(ii)` the depression of the spring under the weight of the body `(` take `g=10N//kg)` and `(iii)` the period of oscillation, if the body is left free.
View SolutionThe period of oscillation of a mass m suspended by an ideal spring is 2s. If an additional mass of 2 kg be suspended, the time period is increased by 1s. Find the value of m.
View SolutionThe frequency of oscillations of a mass m suspended by a spring is `v_(1)`. If the length of the spring is cut to one-half the same mass oscillates with frequency `v_(2)`. Determine the value of `v_(2)//v_(1)`
View SolutionThe periodic time of a mass suspended by a spring (force constant k) is T. if the spring is cut in three equal pieces, what will be the force constant of each part? If the same mass be suspended from one piece, what will be the periodic time?
View SolutionThe time period of a body suspended by a spring be T. what will be the new period, if the spring is cut into two equal parts and when (i) the body is suspended from one part (ii) the body is suspended from both the parts connected in parallel.
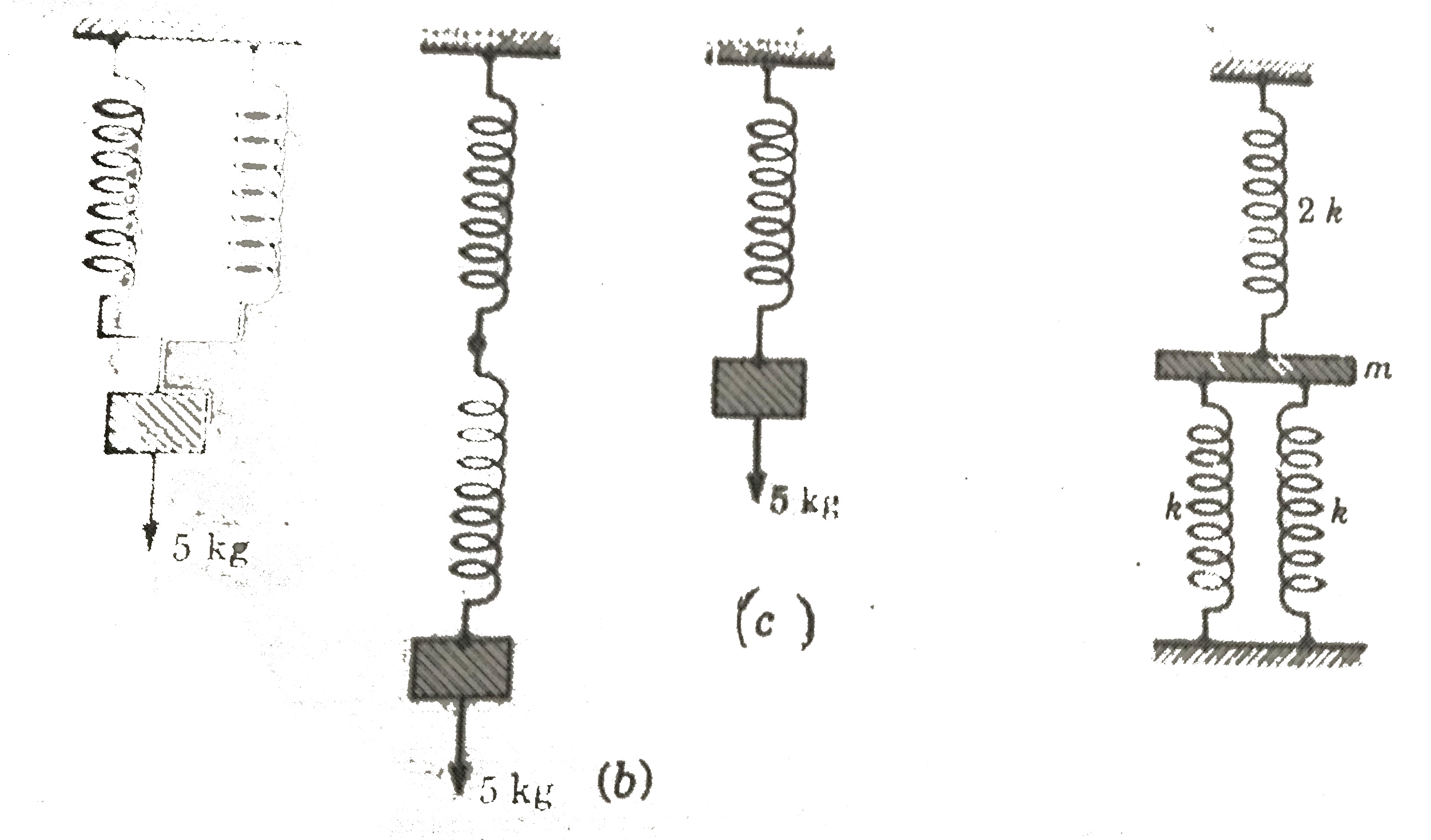
View SolutionTwo identical springs have the same force constant of `147Nm^(-1)`. What elongation will be produced in each spring in each case shown in figure. Take `g=9.8ms^(-2)`
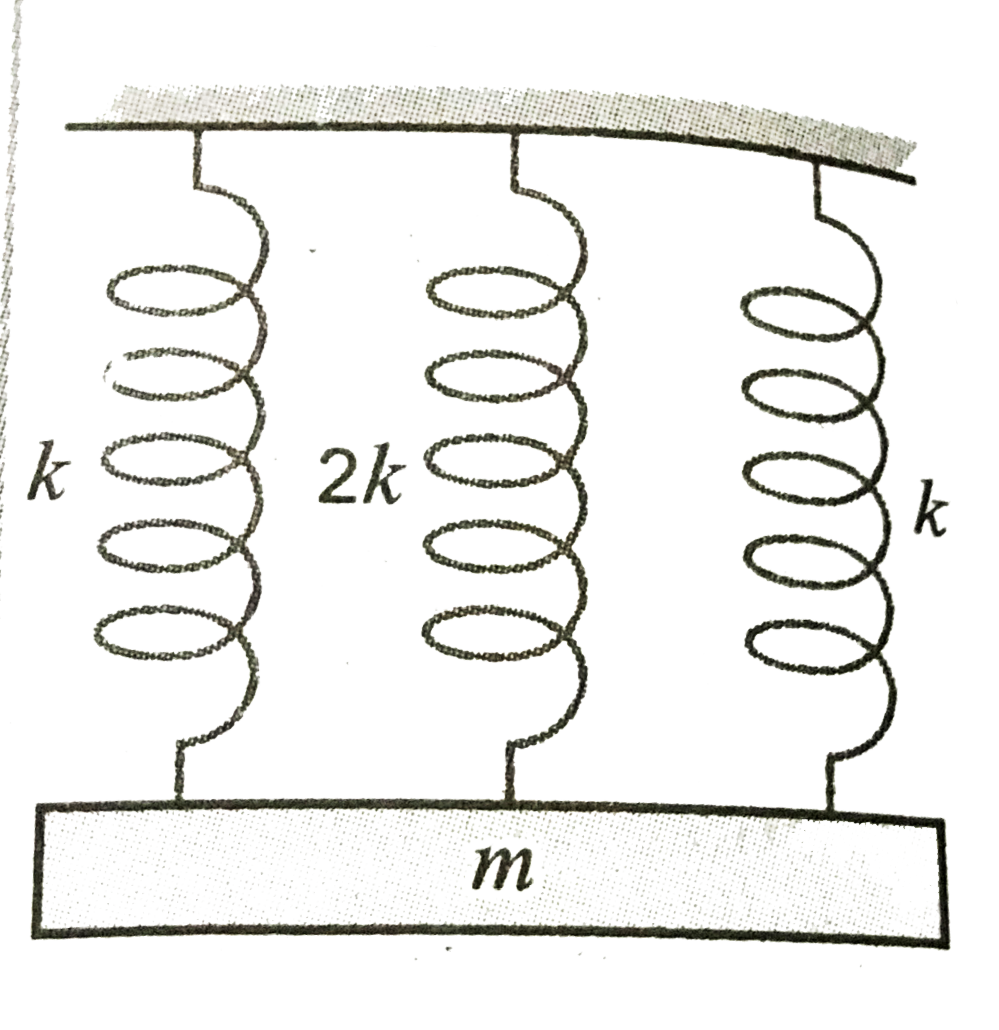
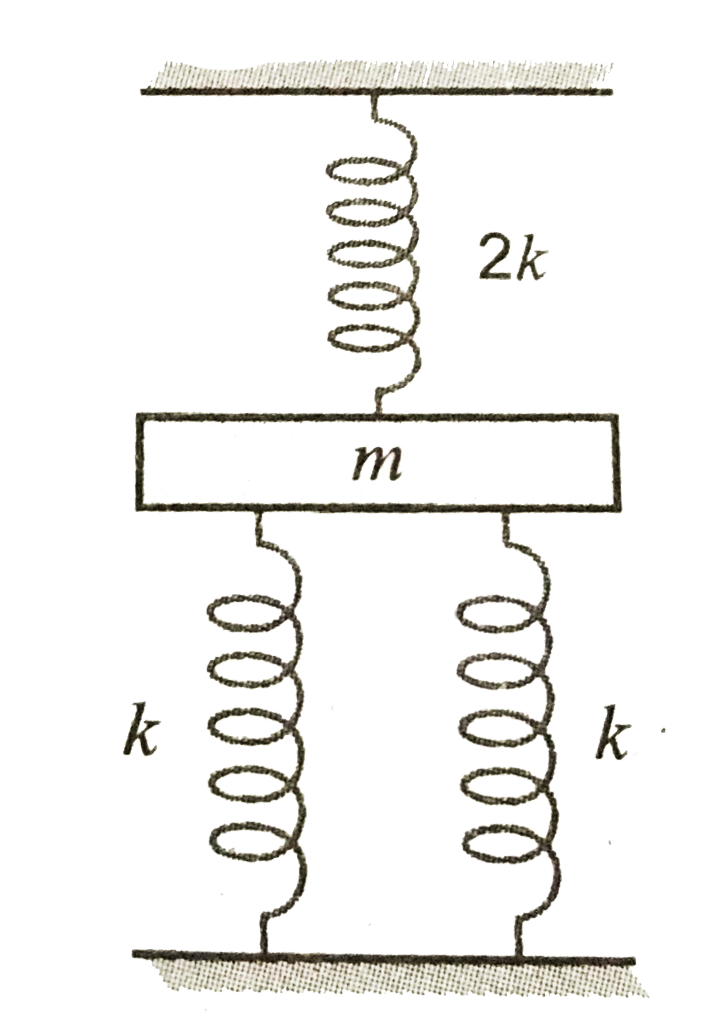
View SolutionThree springs are connected to a mass m as shown in figure, When mass oscillates, what is the effective spring constant and time period of vibration? Given `k=2Nm^(-1)` and m=80 gram.
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 `Nm^(-1)` slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are `k_(1) and k_(2)`, shown that frequency of oscillation of mass m is

View SolutionThe time taken by a simple pendulum to perform 100 vibration is 8 minutes 9 sec in bombay and 8 minutes 20 sec. in pune. Calcualte the ratio of acceleration due to gravity in bombay and pune.
View SolutionIf the length of second's pendulum is decreased by 2%, how many seconds it will lose per day
View SolutionIf the length of a second's pendulum is increased by `1%` , how many seconds will it loss or gain in a day ?
View SolutionIf the length of a simple pendulum is increased by 45% what is the percentage increase in its time period?
View SolutionA second's pendulum is taken to a height where the value of g is `4.36ms^(-2)`. What will be its new time period?
View SolutionA simple pendulum whose length is 20 cm is suspended from the ceiling of a lift which is rising up with an acceleration of `3.0ms^(-2)`. Calculate the time-period of the pendulum.
View SolutionWhat will be the time period of second's pendulumm if its length is doubled?
View SolutionA pendulum 1 m long makes 20 vibrations in 40s. Find the time taken to make 30 vibrations, if its length is increased to 4 m.
View SolutionA second's pendulum is taken from a place where `g=9.8 ms^(-2)` to a place where `g=9.7 ms^(-2)` .How would its length be changed in order that its time period remains unaffected ?
View SolutionIf the acceleration due to gravity on the moon is one-sixth of that on the earth. What will be the change in length of a second pendulum there so that it may beat a second there? Take acceleration due to gravity on earth's surface `=9.8 ?`
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA wooden cylinder of mass 20 g and area of cross-section `1 cm^(2)` , having a piece of lead of mass 60g attached to its bottom,floates in water. The cylinder is depressed and then released.The frequency of oxdillations is `( N )/(pi ) S^(-1)`. Find the value of N. [Neglect the volume of water displaced by the lead piece, take `g =9.8m//s^(2) `,density of water `rho_(w ) = 1 g cm^(-3) ` ]
View SolutionIf the earth were a homogeneous sphere of radius R and a straight hole bored in it through its centre, show that a body dropped into the hole will execute SHM and find its time period.
View SolutionA weighted glass tube is floating in a liquid with 20cm of its length immresed. It is pushed down through a certain distance and then released. Show that up and down motion executed by the glass tube is SHM and find the time period of vibration. Given `g=980cm s^(-2)`.
View SolutionA sphere hung with a wire `60^(@)` rotation of the sphere about the wire produces a restoring torqueof 4.1Nm. If the moment of inertis of the sphere is 0.082 kg `m^(2)`. Find the frequencyof angular oscillations.
View SolutionA lactometer whose mass is 0.2kg is floating vertically in a liquid of relative density 0.9. Area of cross-section of the mariked portion of lactometer in `0.5xx10^(-4)m^(2)`. If it is dipped down in the liquid slightly and released, what type of motion will it execute? what will be its time-period?
View SolutionA body weighing 10g has a velocity of `6cms^(-1)` after one second of its starting from mean position. If the time period is 6 seconds. Find the kinetic energy, potential energy and the total energy.
View SolutionCalculate the energy possessed by a body of mass 20g executing SHM of amplitude 1cm and time peeriod 4s.
View SolutionA bob of simple pendulum of mass 1g is oscillating with a frequency 5 vibrations per second and its amplitude is 3cm. Find the kinetic energy and kinetic energy at that instant.
View SolutionA oscillator of mass 10kg has a velocity of 5 `ms^(-1)` after 1 second of its crossing the mean position. If the time period is 5s. Find the potential energy and kinetic energy at that instant.
View SolutionA particle executes SHM of period 8 seconds. After what time of its passing through the mean position will the energy be half kinetic and half potential ?
View SolutionThe total energy of a partical executing simple harmonic motion of period `2pi` seconds is 10,240erg. The displacement of the particle at `pi//4` second is `8sqrt(2)cm`. Calculate the amplitutde of motion and mass of the particle
View SolutionThe force constant of a weightless spring is `16 N m^(-1)`. A body of mass `1.0 kg` suspended from it is pulled down through `5 cm` and then released. The maximum energy of the system (spring + body) will be
View SolutionA body of mass 0.50kg is executing SHM Its period is 0.1 s and amplitude 10cm. When the body is at a distance of 5cm from the mean postion, find i its accelration ii force acting upon it and ii its potential energy.
View SolutionA particle which is attached to a spring oscillates horizontally with simple harmonic motion with a frequency of `1//pi` Hz and total energy of 10J. If the maximum speed of the particle is `0.4ms^(-1)`, what is the force constant of the spring? What will be the maximum potential energy of the spring during the motion?
View SolutionTwo exactly identical simple pendulums are oscillating with amplitude 2 cma dn 6cm Calculate the ratio of their energies of oscillation.
View SolutionThe length of a weigtless spring increaes by 2cm when a weight of 1.0kg in the period of oscillation of the spring and its kinetic energy of oscillation. Take `g=10ms^(-2)`.
View Solution
Problems for self practice questions and complete solutions for chapter OSCILLATIONS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11