Complete Solutions to Type B Based on Oscillations of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| SL ARORA | Type B Based on Oscillations |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A mass of 2 kg is suspended from a vertical spring. An additional force of 2.5 N stretches it by 1 cm. (i) Calculate the force constant. (ii) Calculate the frequecny of oscillations, if the spring is stretched by the given force and then released.
View SolutionA small body of mass 0.1 kg is undergoing SHM of amplitude 1.0m and period 0.2 s. (i) What is the maximum force acting on it ? (ii) If the oscillations are produced by a spring, what is the force constant of the spring ?
View SolutionThe pan attached to a spring balance has a mass of 1 kg. A weight of kg when placed on the pan stretches the spring by 10 cm. What is the frequency with which the empty pan will oscillate ?
View SolutionA spring compressed by 0.2 m develops a restoring force of 25 N. A body of mass 5 kg is placed over it. Deduce (i) force constant of the spring (ii) the depression of the spring under the weight of the body and (iii) the period of oscillation, if the body is disturbed. Take `g=10 N kg^(-1)`.
View SolutionA spring balance has a scale that reads from 0 to 50kg. The length of the scale is 20cm. A body suspended from this spring, when displaced and released, oscillates with period of 0.60s. What is the weight of the body?
View SolutionA body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant `2.0xx10Nm^(-1)`. What is the stretched length of the spring ? If the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass ? (Neglect the mass of the spring).
View SolutionFor the motion of the mass suspended by a coil spring in example 32.
(i) What is the net force on the suspended mass at its lowermost position ?
(ii) What is the elastic restoring force on the mass due to the spring at its uppermost position ?
View SolutionA spring of force constant `1200Nm^(-1)` is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionIn example 34, let us take the position of the mass, when the spring is unstretched, as x=0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass, if at the moment we start the stop watch (t=0), the mass is (i) at the mean position (ii) at the maximum stretched position (iii) at the maximum compressed position.
In what do these different functions of SHM differ ? Frequency, amplitude or initial phase ?
View SolutionAn impulsive force gives an initial velocity of- `1.0 m s^(-1)` to the mass in the unstretched spring position [sec Fig. 16.2]. What is the amplitude of motion ? Give x as a function of time t for the oscillating mass. Given m=3 kg and `k=1200 Nm^(-1)`.
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 `Nm^(-1)` slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA small trolley of mass 2.0 kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation at a speed of 300 rpm, the length of the stretched spring is 40 cm. If the original length of the spring is 35 cm, determine the force constant of the spring.
View SolutionTwo masses `m_(1)=1.0 kg and m_(2)=0.5 kg ` are suspended together by a massless spring of force constant, `k=12.5 Nm^(-1)`. When they are in equillibrium position, `m_(1)` is gently removed. Calculate the angular frequency and the amplitude of oscillation of `m_(2)`. Given `g=10 ms^(-2)`.
View Solutionfour different springs arrangements. If the mass m in each arrangement is displaced from its equilibrium position and released, what is the resulting frequency of vibration in each case? Neglect the mass of the spring. Figure (a) and (b) represent an arrangement of springs in parallel and (c) and (d) represent springs in series?

View SolutionTwo identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
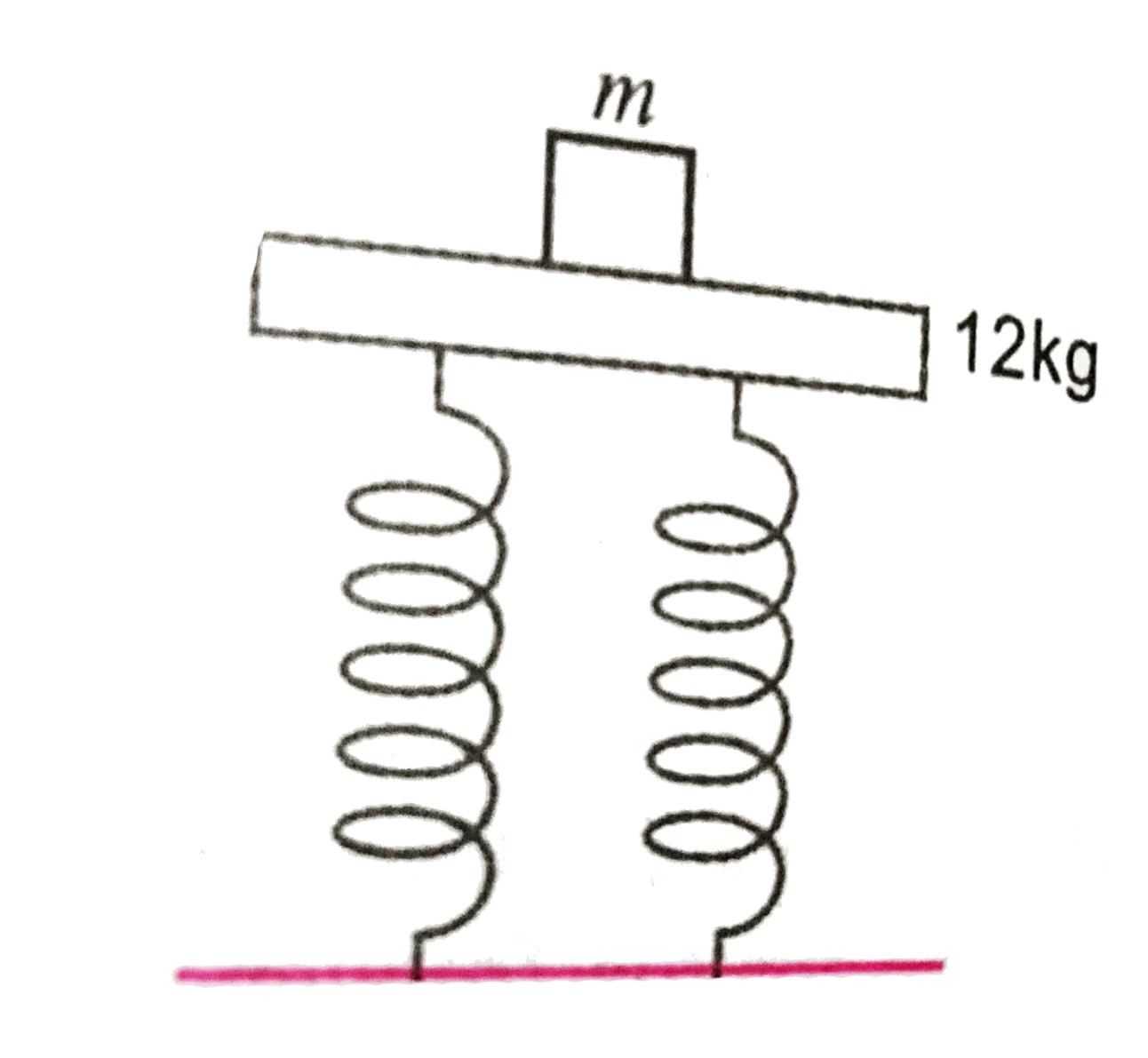
View SolutionA tolley of mass 3.0kg is connected to two identical spring each of force constant `600Nm^(-1)` as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View Solution
Type B Based on Oscillations questions and complete solutions for chapter OSCILLATIONS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11