Complete Solutions to JEE Main And Advanced of chapter MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
A particle moves in a circle of radius `R`. In half the period of revolution its displacement is …………… and distance covered is …………... .
View SolutionFour person K,L,M and N are initally at the corners of a square of side of length d. If every person starts moving, such that K always heads towards L, L heads towards M, M heads directly towards N and N heads towards K, then the four perons will meet after
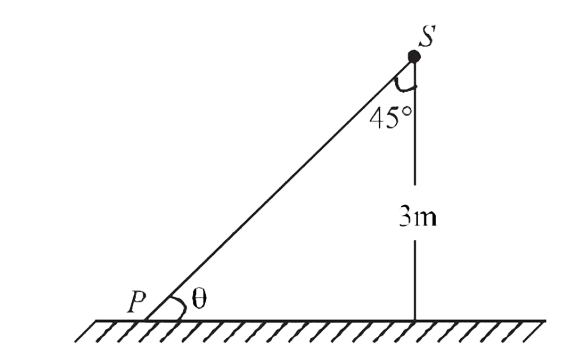
View SolutionSpotlight `S` rotates in a horizontal plane with constant angular velocity of `0.1 ` radian /second. The spot of light `p` moves along the wall at a distance of `3 m ` . The velocity of the spot `p` when `theta = 45(@)` (see - fig. ) is ……….. ` m//s `
View SolutionTwo balls of different masses are thrown vertically upwards with the same speed . They pass through the point of projection in their downward motion with the same speed ( Neglect air resistance ).
View SolutionA projectile fired from the ground follows a parabolic path. The speed of the projectile is minimum at the top of its path.
View SolutionState whether the statement given below is true or false, giving reason in brief: "Two identical trains are moving on rails along the equator on the earth in opposite directions with the same speed. They will exert the same pressure on the rails"
View SolutionA river is flowing from west to east at a speed of ` 5` metres per minute . A man on the south bank of the river , capable of swimming at `10` metres per minute, in still water , wants to swim across the river in the shortest time . He should swim in a direction
View SolutionA boat which has a speed of `5 km` per hour in still water crosses a river of width 1 km along the shortest possible path in fifteen minutes. The velocity of the river water in km per hour is :-
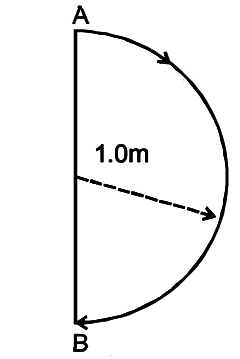
View SolutionIn `1.0 s`, a particle goes from point `A` to point `B` , moving in a semicircle of radius `1.0 m ` (see figure ). The magnitude of the average velocity
View SolutionA ball is dropped vertically from `a` height `d` above the ground . It hits the ground and bounces up vertically to a height ` (d)/(2)`. Neglecting subsequent motion and air resistance , its velocity `v` varies with the height `h` above the ground as
View SolutionA particle starts sliding down a frictionless inclined plane. If ` S_(n) ` is the distance travelled by it from time ` t = n-1 sec `, to `t = n sec`, the ratio ` (S_(n))/(s_(n+1))` is
View SolutionA body starts from rest at time `t = 0` , the acceleration time graph is shown in the figure . The maximum velocity attained by the body will be
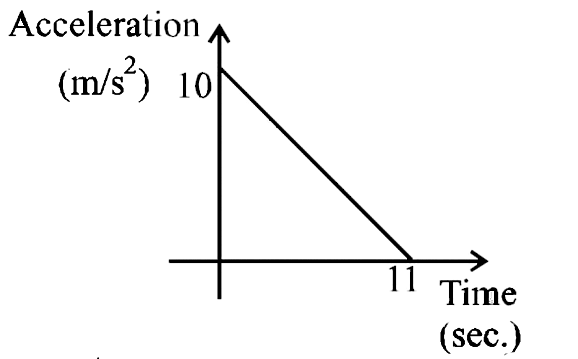
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View SolutionTwo identical discs of same radius `R` are rotating about their axes in opposite directions with the same constant angular speed `omega` . The discs are in the same horizontal plane. At time `t = 0` , the points `P` and `Q` are facing each other as shown in the figure. The relative speed between the two points `P` and `Q` is `v_(r)`. In one time period `(T) ` of rotation of the discs , `v_(r)` as a function of time is best represented by
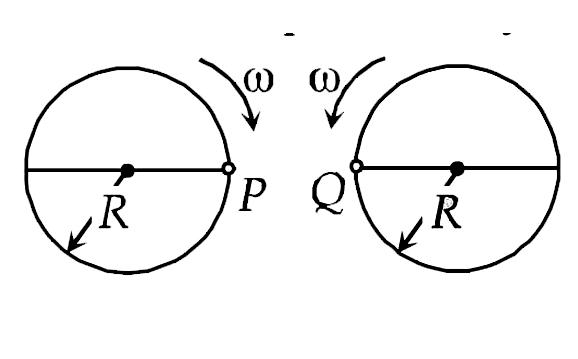
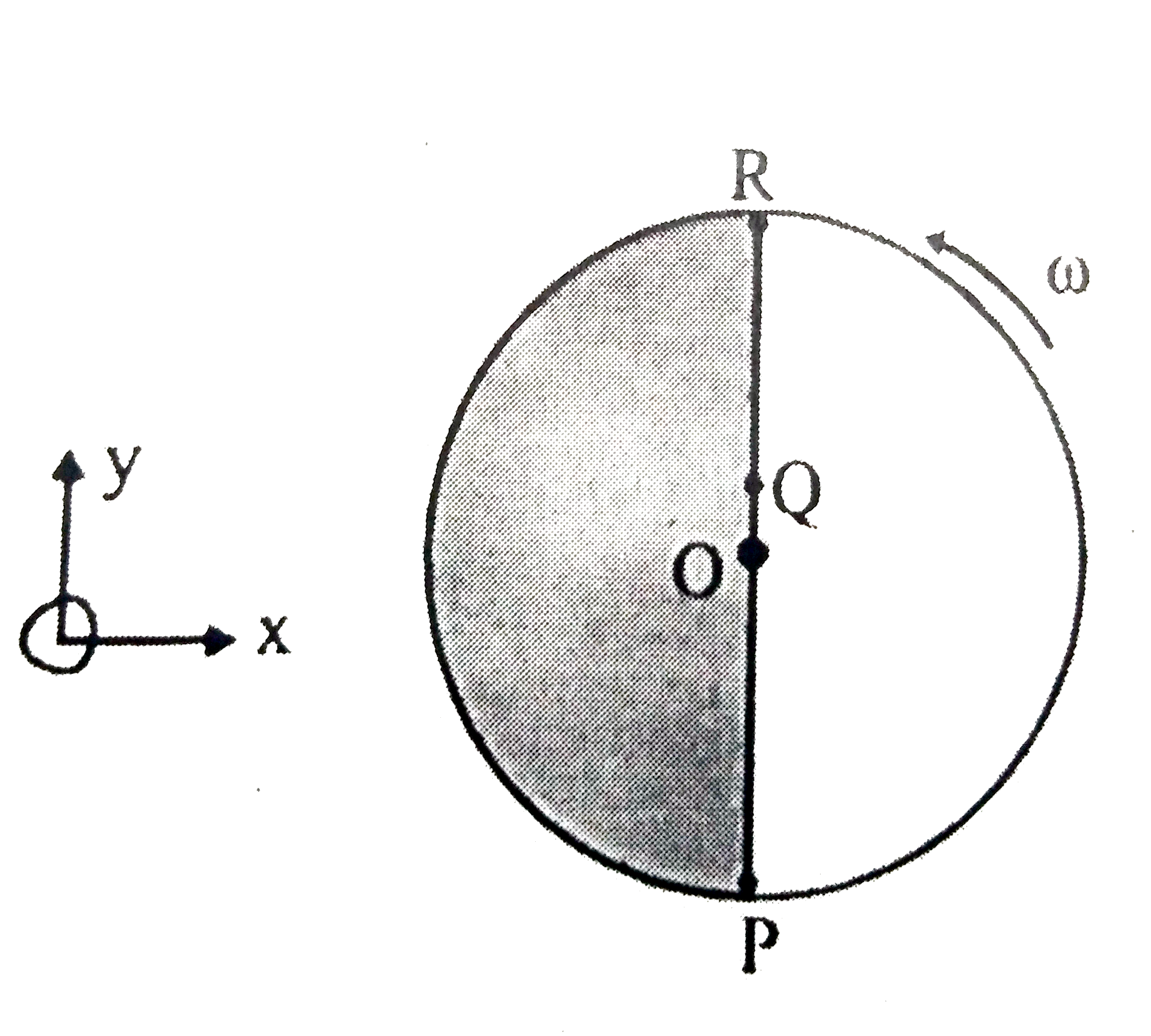
View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed `omega` about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed `(1)/(8)` rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
View SolutionA particle is moving eastwards with a velocity of ` 5 m//s`. In `10 s` the velocity changes to `5 m//s` nothwards. The average acceleration in this time is
View SolutionA particle of mass `m` moves on the ` x- axis ` as follows : it starts from rest at ` t = 0`, from the point `x = 0`, and comes to rest at ` t = l` at the point `x = 1`. No other information is available about its motion at intermediate times `( 0 lt t lt l)` . If `alpha ` denotes the instantaneous accelartion of the particle , then :
View SolutionThe coordinate of a particle moving in a plane are given by ` x(t) = a cos (pt) and y(t) = b sin (pt)` where `a,b (lt a)` and `P` are positive constants of appropriate dimensions . Then
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionThe displacement `x` of particle moving in one dimension, under the action of a constant force is related to the time `t` by the equation ` t = sqrt(x) +3`
where `x` is in meters and `t` in seconds . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first ` 6 seconds`.
View SolutionAnswer the following giving reasons in brief :
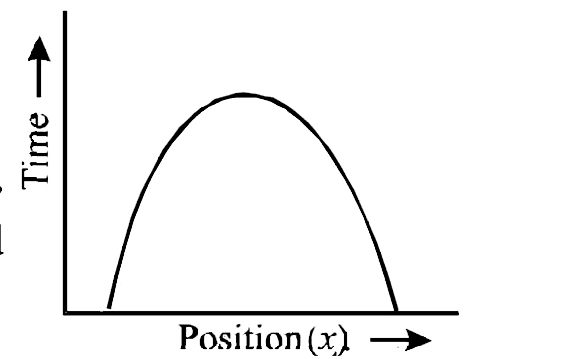
Is the time variation of position , shown in the figure observed in nature ?
View SolutionParticles P and Q of mass 20g and 40g respectively are simu ltaneously proejected from points A and B on the ground. The initial velocities of P and Q make `45^(@)` and `135^(@)` angles respectivley with the horizontal AB as shown in the Fig. 5.44 Each particle has an initial speed of 49m/s . the separation AB is 249m. both particles travel in the same vertical plane and undergo a collision. After collision P retraces its path. Determine the position of q when it hits the grou.d How much time after the collision does the particle Q take to reach the ground? (Take g`=9.8m//s^(2)`)

View SolutionTwo towers AB and CD are situated at a distance d apart, as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown fromt the top of CD at an angle of `60^(@)` to the horizontal towards AB with the same magnitude of initial velocity as that oft he first object. The two objects move in the same vertical plane, collide in mid air and stick to each other (i) calculate the distance between the towers and (ii) find the position where the objects hit the ground.

View SolutionTwo guns situated at the top of a hill of height `10 m` fire one shot each with the same speed `5sqrt(3) m//s` at some interval of time. One gun fires horizontal and the other fores upwards at an angle of `60^(@)` with the horizontal. Two shots collide in air at a poit `P`. Find (i) time-interval between the firing and (ii) coordinates of the point `P`. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the `x-y` plane.
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination `theta` . From a point `P` on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is `u` , and the direction of projection makes an angle `alpha` with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection `p` and the point `Q` where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

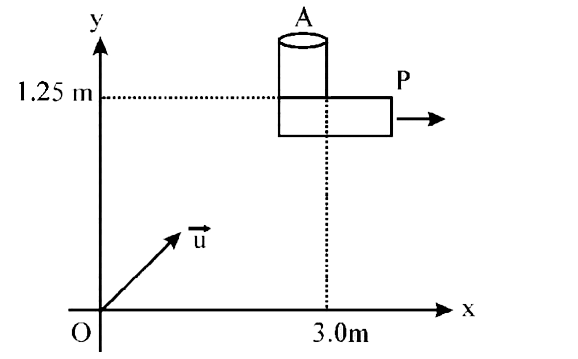
View SolutionAn object `A` is kept fixed at the point ` x= 3 m` and `y = 1.25 m` on a plank `p` raised above the ground . At time ` t = 0 ` the plank starts moving along the `+x` direction with an acceleration ` 1.5 m//s^(2) `. At the same instant a stone is projected from the origin with a velocity `vec(u)` as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle ` 45^@` to the horizontal . All the motions are in the ` X -Y `plane . Find ` vec(u)` and the time after which the stone hits the object . Take ` g = 10 m//s`
View SolutionOn a frictionless horizontal surface , assumed to be the ` x-y` plane , a small trolley `A` is moving along a straight line parallel to the `y-axis `( see figure) with a constant velocity of `(sqrt(3)-1) m//s ` . At a particular instant , when the line `OA` makes an angle of `45(@)` with the `x - axis ` , a ball is thrown along the surface from the origin `O`. Its velocity makes an angle `phi` with the x -axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle `theta` made by the velocity vector of the ball with the x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ` phi = (4 theta )//(4)`.

View SolutionSTATEMENT -1 : For an observer looking out through the window of a fast moving train , the nearby objects appear to move in the opposite direction to the train , while the distant objects appear to be stationary .
STATEMENT - 2 : If the observer and the object are moving at velocities ` vec v_(1)` and `vec v_(2)` respecttively with refrence to a laboratory frame , the velocity of the object with respect to a laboratory frame , the velocity of the object with respect to the observer is `vecv_(2) - vecv(1) ` .
(a) Statement -1 is True, statement -2 is true , statement -2 is a correct explanation for statement -1
(b) Statement 1 is True , Statement -2 is True , statement -2 is NOT a correct explanation for statement -1
(c) Statement - 1 is True , Statement -2 is False
(d) Statement -1 is False, Statement -2 is True
View SolutionA train is moving along a straight line with a constant acceleration a. A body standing in the train throws a ball forward with a speed of `10ms^(-1)`, at an angle of `60^(@)` to the horizontal . The body has to move forward by 1.15 m inside the train to cathc the ball back to the initial height. the acceleration of the train. in `ms^(-2)` , is:
View SolutionA ball whose kinetic energy is `E` , is projected at an angle of `45^@` to the horizontal . The kinetic energy of the ball at the highest point of its flight will be
View SolutionFrom a building two balls `A` and `B` are thrown such that `A` is thrown upwards and `B` downwards ( both vertically with the same speed ). If `v_(A) and v_(B)` are their respective velocities on reaching the ground , then
View SolutionA car , moving with a speed of `50 km//hr` , can be stopped by brakes after at least ` 6m `. If the same car is moving at a speed of `100 km//hr`, the minimum stopping distance is
View SolutionA boy playing on the roof of a `10 m` high building throws a ball with a speed of `10 m//s` at an angle of `30(@)` with the horizontal. How far from the throwing point will the ball be at the height of `10 m` from the ground ?
`[ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]`
View SolutionThe co-ordinates of a moving particle at anytime 't' are given by ` x = alpha t^(3) and y = beta t^(3)`. The speed of the particle at time 't' is given by
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in `T/3` second?
View SolutionIf `vec(A) xx vec(B) = vec(B) xx vec(A)`, then the angle between `A to B` is
View SolutionA projectile can have the same range 'R' for two angles of projection . If `'T_(1)'` and `'T_(2)'` to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
View SolutionWhich of the following statements is FALSE for a paricle moving in a circle with a constant angular sppeed?
View SolutionAn automobile travelling with a speed `60 km//h` , can brake to stop within a distance of `20 m` . If the car is going twice as fast i. e. , `120 km//h`, the stopping distance will be
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
View SolutionA car, starting from rest, accelerates at the rate (f) through a distance (S), then continues at constant speed for some time (t) and then decelerates at the rate ` f//2` to come to rest. If the total distance is ` 5 S`, then prove that
` S=1/2/ ft^(2)`.
View SolutionA particle is moving eastwards with a velocity of ` 5 ms_(-1)`. In `10 seconds` the velocity changes to `5 ms^(-1)` northwards. The average acceleration in this time is
View SolutionThe relation between time `t` and distance `x` is `t = ax^(2)+ bx` where `a and `b` are constants. The acceleration is
View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive ` x-direction` with a velocity 'v' that varies as ` v = a sqrt(x)`. The displacement of the particle varies with time as
View SolutionA particle is projected at ` 60(@)` to the horizontal with a kinetic energy `K` . The kinetic energy at the highest point is
View SolutionThe velocity of a particle is `v = v_(0) + gt + ft^(2)`. If its position is ` x=0 ` at ` t= 0 `, then its displacement after unit time `( t = 1 )` is
View SolutionA body is at rest at ` x =0 ` . At ` t = 0`, it starts moving in the positive `x - direction` with a constant acceleration . At the same instant another body passes through ` x= 0 ` moving in the positive ` x - direction ` with a constant speed . The position of the first body is given by `x_(1)(t)` after time 't', and that of the second body by ` x_(2)(t)` after the same time interval . which of the following graphs correctly describes `(x_(1) - x_(2))` as a function of time 't' ?
View SolutionConsider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
View SolutionA particle has an initial velocity of `3hat(i) + 4 hat(j)` and an acceleration of `0.4 hat(i) + 0.3 hat(j)`. Its speed after `10s ` is :
View SolutionA particle is moving with velocity ` vecv = k( y hat^(i) + x hat(j)) `, where `k` is a constant . The genergal equation for its path is
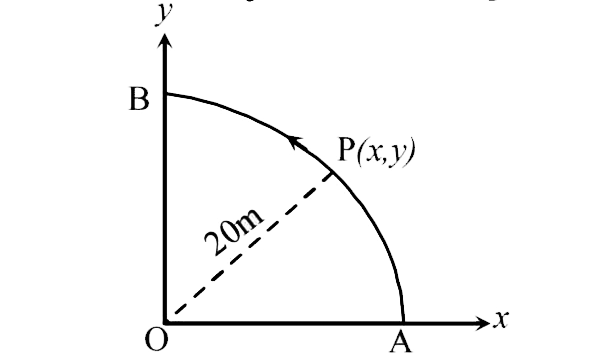
View SolutionA point `p` moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length `s = t^(3) + 5 ` , where `s` is in metres and ` t` is in seconds . The radius of the path is `20 m` . The acceleration of 'P' when ` t = 2 s` is nearly .
View SolutionFor a particle in uniform circular motion , the acceleration ` vec(a)` at a point ` p ( R, theta )` on the circle of radiu ` R` is ( Here ` theta` is measured from the ` x- axis` )
View SolutionA small particle of mass ` m` is projected at an angle `theta` with the ` x`- axis with an initial velocity ` v_(0)` in the ` x-y `plane as shown in the figure . At a time ` t lt ( v_(0) sin theta)/(g) `, the angular momentum of the particle is
where `hat (i) , hat (j) and hat(k)` are unit vectors along `x , y and z` - axis respectively.
View SolutionAn object , moving with a speed of ` 6.25 m//s `, is decelerated at a rate given by :
`(dv)/(dt) = - 2.5 sqrt (v)` where `v` is the instantaneous speed . The time taken by the object , to come to rest , would be :
View SolutionA water fountain on the ground sprinkles water all around it. If the speed of water coming out of the fountains is v, the total area around the fountain that gets wet is:
View SolutionA boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that the boy can throw the same stone up to will be:
View SolutionTwo cars of mass ` m_(1) and m_(2) ` are moving in circle of radii `r_(1) and r_(2) ` , respectively . Their speeds are such that they make complete circles in the same time `t` . The ratio of their centripetal acceleration is :
View SolutionA particle of mass `m` is at rest the origin at time ` t= 0 ` . It is subjected to a force ` F(t) = F_(0) e^(-bt)` in the `x` - direction. Its speed ` v(t)` is depicted by which of the following curves ?
View SolutionA projectile is given an initial velocity of ` ( hat(i) + 2 hat (j) ) m//s`, where ` hat(i)` is along the ground and `hat (j)` is along the vertical . If ` g = 10 m//s^(2) `, the equation of its trajectory is :
View SolutionFrom a tower of height `H`, a particle is thrown vertically upwards with a speed `u` . The time taken by the particle , to hit the ground , is ` n` times that taken by it to reach the highest point of its path. The relative between ` H, u and n` is :
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff ` 240 m ` high with initial speed of ` 10 m//s and 40 m//s` respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take ` g = 10 m//s^(2))`
( The figure are schematic and not drawn to scale )
View SolutionAirplanes `A` and `B` are flying with constant velocity in the same vertical plane at angles `30^(@)` and `60^(@)` with respect to the horizontal respectively as shown in figure . The speed of `A` is `100sqrt(3) m//s` . At time `t = 0 s`, an observer in `A` finds `B` at a distance of `500 m`. The observer sees `B` moving with a constant velocity perpendicular to the line of motion of `A` . If at `t = t_(0)`, A just escapes being hit by `B ,t_(0)` , A just escapes being hit by `B , t_(0)` in seconds is

View SolutionA rocket is moving in a gravity free space with a constnat acceleration of `2ms^(-1)` along +x direction (see Fig.5.126). The length of a chamber inside the rocket is 4m. A ball is thrown from th left end of the chamber in +x direction with a speed of 0.3 `ms^(-1)` relaitve to the rocket. At the same time , another ball is thrown in -x direction with a speed of 0.2ms^(-1)` from its right and relative to the rocket. the time in seconds when the two balls hit each other is:

View Solution
JEE Main And Advanced questions and complete solutions for chapter MOTION of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11