Complete Solutions to JEE Main And Advanced of chapter WORK, ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY & POWER |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
If maching is lubricated with oil
View SolutionTwo masses of `1 `gas and `4` gas are moving with oqualkinetic energy . The ratio of their liner moment is
View SolutionA particle of mass in is moving in a circular with of constant radius `r` such that its contripetal accelenation `a_(c) ` is varying with time `t` as `a_(c) = K^(2) rt^(2)` where K is a constant . The power delivered to the particles by the force action on it is
View SolutionA spring of Force- constant `K` is cut into two pieces sach that one piece is double the length of the other . Then the long pieces will have a force - constant of
View SolutionA wind - powered generator convets and energy into electrical energy . Assume that the generator convents a fixed fraction of the wind energy intercepited by to blades into electrical energy for wind speed `V` , the electrical power output will be propertional to
View SolutionA particle which is constant to move along the `x- axis` , is subjected to a force in the same direction which varies with the distance `x` of the particle from the origin as `F(x) = -Kx + ax^(3)` . Hero `K` and `a` are positive constant . For `x ge 0`, the fanctional from of the patential every `U(x) of the particle is
View SolutionAn ideal spring with spring - constant `K` is bung from the colling and `a` block of mass `M` is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
View SolutionIf `W_(1) W_(2)` and `W_(3)` represent the work done in moving a particle from `A` to `B` along three different paths `1.2` and`3` respectively (as shown ) in the gravitational fieled of a point mass m, find the correct relation between `W_(1) W_(2)` `W_(3)`
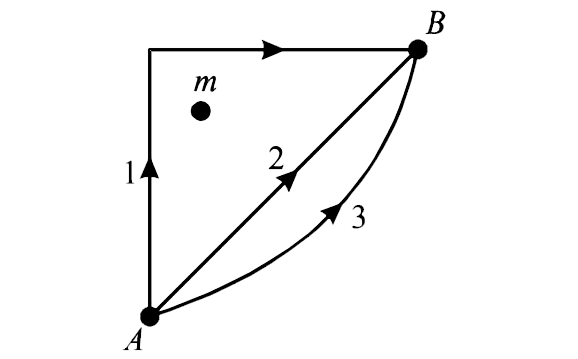
View SolutionA particle is acted by `x` force `F = Kx` where `K` is `a( + Ve)` constant its potential mwrgy at `x = 0` is zero . Which curve correctly represent the variation of putential energy of the block with repect to `x`
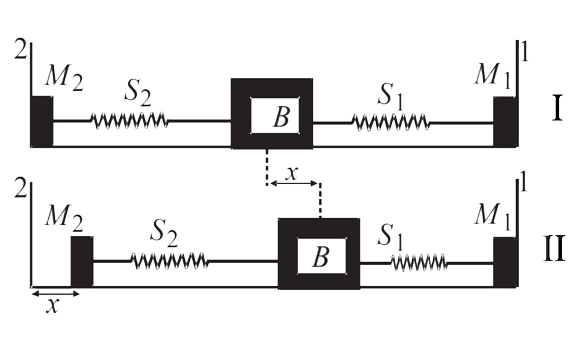
View SolutionA block `(B)` is attached to two unstriched sprig `S_(1)` and `S_(2)` with spring constant `K` and `4K` , respectively (see fig 1) The other ends are atteched in identical support `M_(1)` and `M_(2)` not attached in the walls . The springs and supports have negligible mass . There is no friction anywhere . The block `B` is displaced toword wall `1` by a small distance `z` (figure (ii)) and released . THe block return and moves a maximum displacements `x` and `y` are musured with reoact to the equalibrum of the block `B` and the ratio `y//x` is
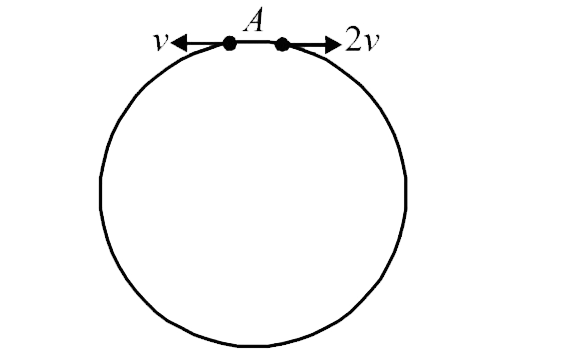
View SolutionTwo small particles of equal masses stant moving in opposite direction from a point `A` in a burtizonetal circule orbic their tangention velocity are `V` and `2V` , respectively as shown in the figure between collsions , the particals move with constant speed After making how many elastic collition , other the then that at `A` these two partical will again reach the point `A` ?
View SolutionA piece of wire is bent in the shape of a parabola `y = Kx^(2)` (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
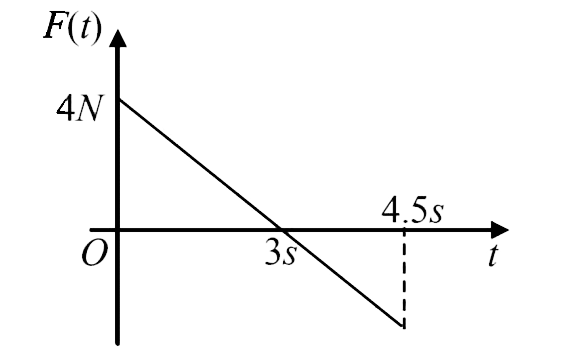
View SolutionA block of mass`2` kg is from to move along the x - axis it is at rest and from `1 = 0` onwards it is subjeted to a time - depended force `F(i) ` in the `x` diretion . The force `F(1) ` varies with `1` as shown in the figure . The kinetic of the block after `4.5` second is
View SolutionThe work done an a particle of mass `m` by a force
`K[(x)/((x^(2) + y^(2))^(3//2)) hati +(y)/((x^(2) + y^(2^(3//2))) hatj)]`
(K being a constant of appropriate dimensions), when the partical is taken from the point `(a,0)` to the point `(0,a)` along a circular path of radius a about the origin in x - y plane is
View SolutionA tennis ball dropped on a barizoontal smooth surface , it because back to its original postion after hiting the surface the force on the bell during the collision is propertional to the length of compression of the bell . Which one of the following skethes desches discribe the variation of its kinetic energy `K` with time `1` mass apporiandly ? The figure as only illistrative and not to the scale .
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body in time `t` is proportional to
View SolutionA uniform chain of length `L` and mass `M` is tying on a smoth table and one third of its length is banging vertically down table the edge of the table if g is acceleration the to gravity , the work required to pull the hanging part on the table is
View SolutionA particle is acted upen by the a force of constant magninude which is always perpendicalar to the velocity of the particle . The motion of the particle taken place is a plane it follows that :
View SolutionA force `F = -K(y hatI + x hatj)`(where `K` is a posive constant ) acts on a particle moving in the `xy` plane . Starting form the original , the partical is taken along in the positive `x` axis to the point `(x,0)` and then partical to they axis the point `(x,0)` . The total work done by the force `F` on the particls is
View SolutionA stone tied to a string of length `L` is whirled in a vertical circle with the ofter end of the string at the centre . At a certin instant of time , the stone is at its lowest position , and has a speed is , the magintube of the change in its velocity as it reached a positive when the string is horizontal is
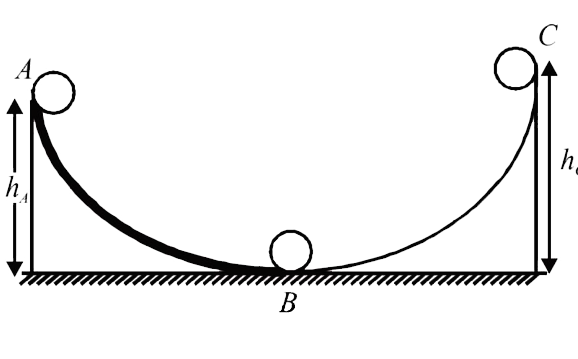
View SolutionA small bell starts moving from `A` over `a` fixed track as shown in the figure . Surface `AB` is friction from `A` to `B` the bell roll ralis without sipping `BC` is friction , `K_(A)K_(B)` and` K_(C)` are kinetic energy of the bell at `A, B` and `C` respacecvely.Then
View SolutionA bullet is fired from rifle . If the rifle recoils freely determine whether the kinetic energy of the rifle is greater then , equal or less then that of the bullet .
View SolutionA spring of force constant `k` is cut into three equal parts what is force constant of each part ?
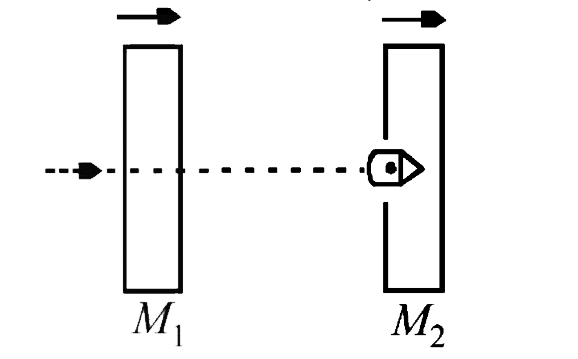
View SolutionA `20 ` gm bullet pierces through a plate of mass `m_(1) = 1` kg and then comes to rest inside a second plate of mass `M_(2) = 2.98` kg as shown , it is found that the two plates initily atrest , now move with equal velocity . Find the percentage loss in the initial velocity of the bullet when it is between `M` and `M_(2)` neglet any loss of material of the pletes due to the action of the bullet
View SolutionWhen a ball is thrown up , the magnitude of its momentum decreases end then increase . Does this violate the conservation of momentum principle ?
View Solution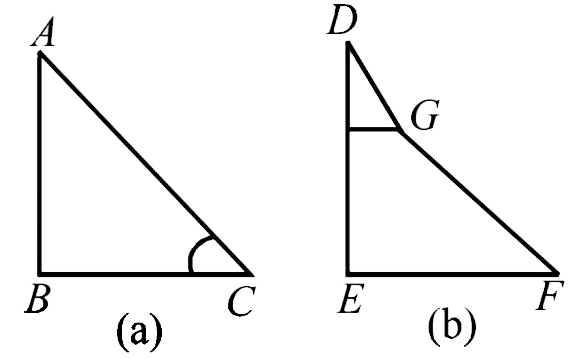
In the figure (a) and (b) `AC` and `GF` are fixed inclined planes `BC = EF = x` and `AB = DE = y` A small block of mass `M` is rdeased from the point `A` it sides down `AC` and maches `C` with a speed `V_(C) ` The same block is relessed from rest from the point `D` it sides down `DGF` and reached the point the `F` with `V_(p)` The coefficients of kiletic friction between the block and the sarface `AC` and `DGF` are `mu` colculate `V_(C) ` and `V_(p)`
View SolutionTwo blocks`A` and`B` are connected to each other by a string and a spring , the spring pases and a frictionless pulley as down over in the figure . Block `B` sides over the horizental top surface of a stationery block `C` both with the verical side of `C` , both with the same conform speed
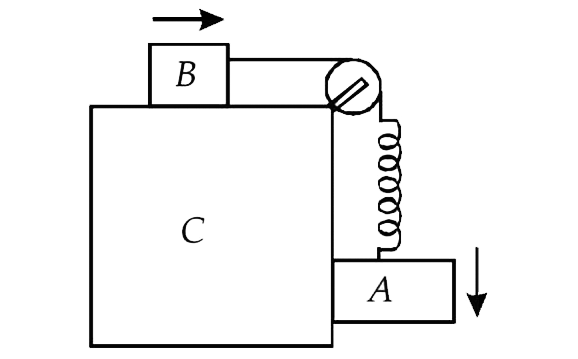
The coefficient of friction between the surface the of block is `0.2` force constant of the spring is `1960` newtons , if mass of block `A` is `2` kg , calculate the mass of block `F` and `B` and the energy stored is the spring
View SolutionA `0.5` kg block sides from the point `A` (see fig) on a hurizontal track as wil initial speed of `3` m//s toward a weightes horizental spring of length `1` in and force constant `2` newtav in the part `AB` of the track is frictionless friction and the per `BC` has the coefficient of the state `AB` and and `BD`are `2` m and `2.14` m repectively , find the total distance through which the block move before if conseto rest completely (Taking` = 10m//s^(2)) ` .
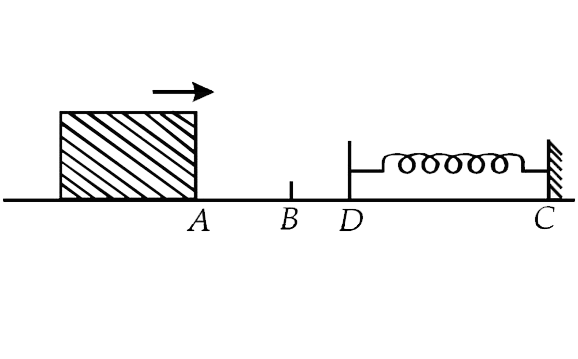
View SolutionA string with one end fixed on a right well , passing over a fixed frictionless pulley at a distance of `2` m from the well , has a point mass `M = 2kg` attached to the it at a distance of I m from the well . A mass `m= 0.5` kg attached at the free end is field at rest as this the
string is horizontal between the wall and the pulley when will be the speed with which the mass `M` with hit the well when the mass `m` is released ?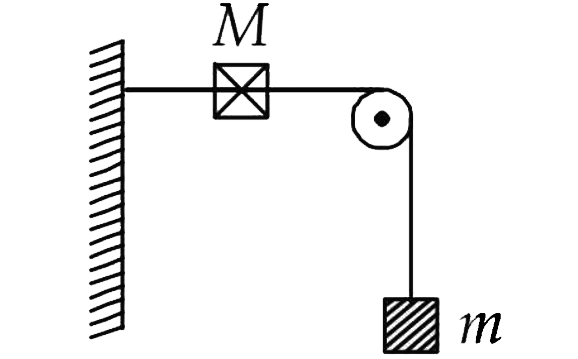
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being `(2)/(sqrt(5)`
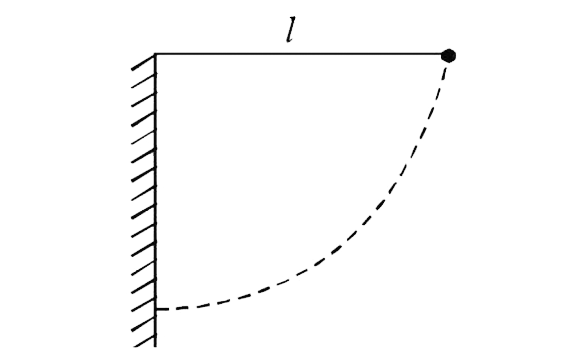
what is the miximum number of colision after which the amplitube of secillections between less that `60` digree ?
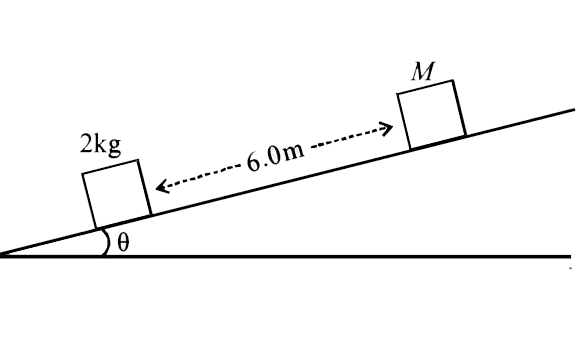
View SolutionTwo blocks of mass `2` kg and `M` are at rest as an inclined plane and are sparated of by a distance of `6.0` m as shown in figure . The coefficient of friction between each of the block and the inclined plane is `0.25` . The `2` kg block is given a velocity of `10.0` m//s up the inclined plate if collied with `M` comes back and has a velocity of `1.0`m//s when if rached its inital position , The ofter block `M` ofter the collisiin its resitition . THe ofter the colition its `0.5` m up and come to rest caleslate the coefficient of resttuion between the block and the mass of the block `M` [Take sin theta +n tan theta = 0.05 and `a = 10m//s^(2)`
View SolutionA spherical balll of mass `m` is the highest point in the space between two fixed , concentic sphere `A` and `B` the smaller the two sphere `A` has a radius `R` and the space between the two spheres has a width `d` . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by `theta` (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle `theta`
(b) Let N_(A)` and N_(B)`denote in the magnitubes of the normal reaction force on the bell evered by the sphare `A` and `B` repectively Skech the variation of `N_(A) and`N_(B)` as functions of `cos theta ` in the range `0 le theta le pi ` by drawing two separate graph in your answer book taking `cos theta ` an the horizental axas.
View SolutionA small block of mass `M` move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from `60^(@)` to `30^(@)` at point `B` . The block is initally at rest at `A` Assume the collsion between the block and the incline are totally inclassic `(g = 10m//s^(2)`)
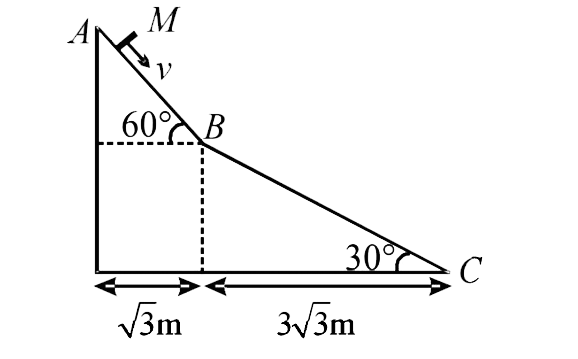
The speed of the block at point `B` immedutaly after it strikes the second inclime is -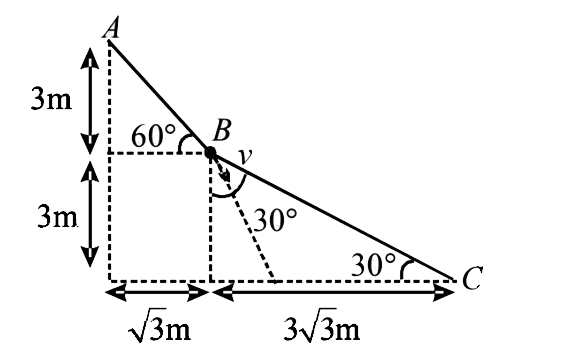
View SolutionA small block of mass `M` move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from `60^(@)` to `30^(@)` at point `B` . The block is initally at rest at `A` Assume the collsion between the block and the incline are totally inclassic `(g = 10m//s^(2)`)
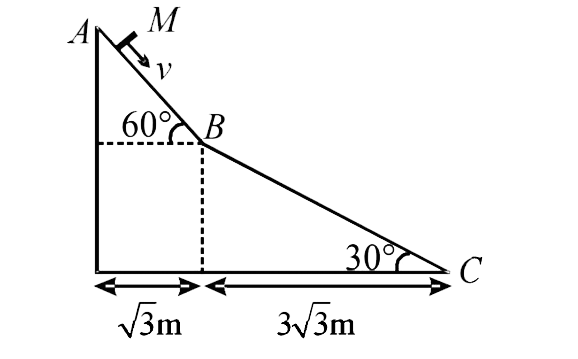
The speed of the block at point `C` immediately before is leaves the second incline is
View SolutionA small block of mass `M` move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from `60^(@)` to `30^(@)` at point `B` . The block is initally at rest at `A` Assume the collsion between the block and the incline are totally inclassic `(g = 10m//s^(2)`)
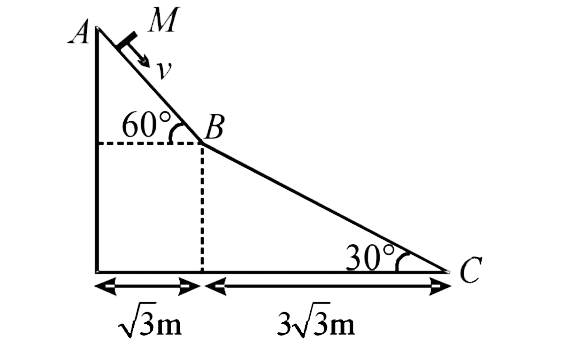
If collision between the block and the incline is completely elestic , then the vartical (apward) component of the of the block at point `B` immediatly after it stricess the scond indine is -
View SolutionA small block of mass `1` kg is a circular are of ratius `40` m . The block sides along the track without topping and a frictionnal force acts on it in the direction opposite in the instrmens velocity . The work done in evercoming the friction up to the point `Q` as shown is the figure below is `150 J`
(Take the acceleration due to gravity `g = 10 ms^(-2))`
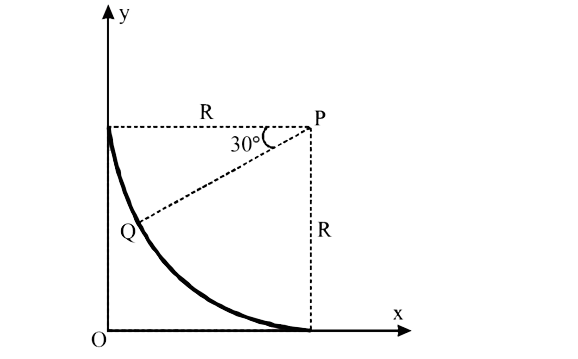
The magnitude of the normal reaction that acts on the block at the point `Q` is
View SolutionA small block of mass `1` kg is a circular are of ratius `40` m . The block sides along the track without topping and a frictionnal force acts on it in the direction opposite in the instrmens velocity . The work done in evercoming the friction up to the point `Q` as shown is the figure below is `150 J`
(Take the acceleration due to gravity `g = 10 ms^(-2))`
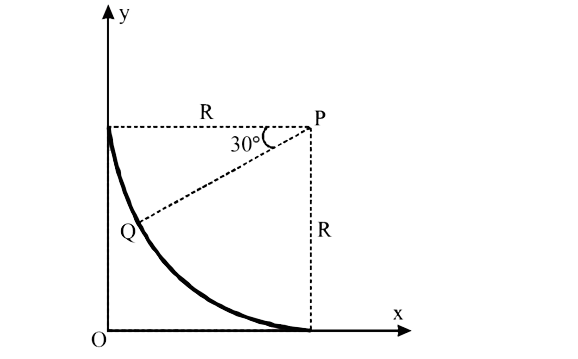
The speed of the block when it reaches the point `Q` is
View SolutionStatement - 1 : A block of mass `m` starts moving an a rough horizental surface with `x` velocity `x` it step dus to friction between the block and the surface is now tihed in an angles a cormin distance . The surface is now tilted is an angle on the `30^(@)` with the inrizonal and the same block is to go up on the surface with the same inital velocity `x` .THe decrease in the mechanical energy is the second situation is smailar then the that the first situation
Statment -2 : The coeifficient of friction between the block and the surface dicreases with the increses in the angle of inclimation .
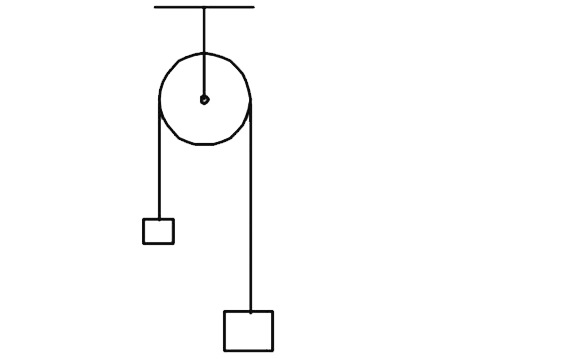
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it `0.36` kg and `0.72` kg Taking `g = 10 ms^(-2)` , find the work done by the string on the block of mass ` 0.36` kg doring the first second after the system is refosed from rest ,
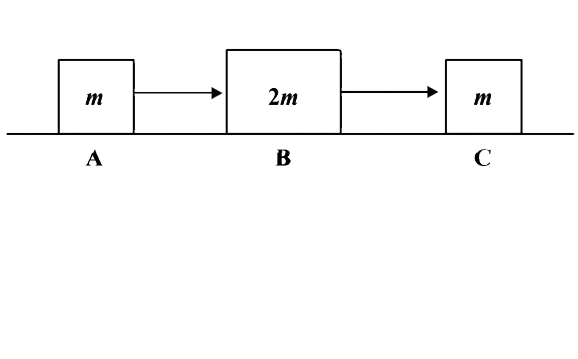
View SolutionThere object `A ,B` and `C` are kept is a straing line a fritionlas horizental surface . These have masses have increase on `2m` and `m` repectively . The object `A` move toward `B` with a speed `9` m//s and makes as electic collision with a there after `B` makes complately inclesis with `C` . All motion over on the same strangth line . Find the first speed of the object `C`
View SolutionA block of mass `0.18 kg ` is attached to a spring of force constant `2 N//m` The coefficient of friction between the block and the force is `0.1` insitially its block is at rest and the block as spring is an streched , As impalse is given to the block as shown in the figure . The block sides a distance of ` 0.06` in and comes to the first time . The initial velocity of the for blocks is mis `V = N 10` then `N` is .
View SolutionA particle of mass `0.2` kg is moving is one dimension under a force that delever is a constant preses `0.5 W` in the particle . If the detail speed `(n ms^(-1))` of the particle is zero , the speed`(mms^(-1))` after `5 xx` is
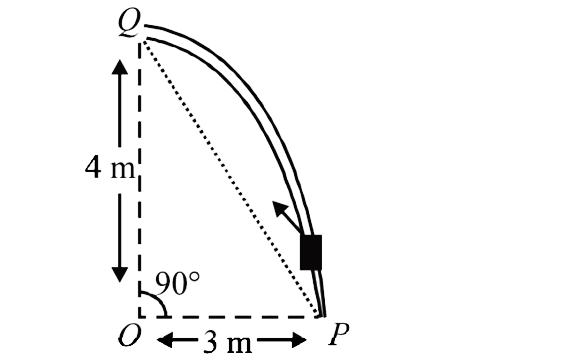
View SolutionConstant as eliptical rail `PQ` in the varticle plain with `OP = = 3m ` and `OQ= 4 m` . A block of mass `1` kg is pailed along the rail from `P` to `Q` with a force of `18 N` , which is always parallel to less `PQ` Assuming are frictionless losess , the kinetic energy the block when `0` reches `Q` is `( nxx 10)` pales . THe velie of a (Take acceleration due to gravity ) `= 10ms^(-2))`
View SolutionConstant the following two statements :
A. Liner momentum of a system of particles is zero
B . Kinetic energy of a system of particls is zero .Then
View SolutionA wire suspended vertically from one of itsends is strached by attached a weight of `200 N` to the lower end . The weight streches the wire by `1 mm` . Then the elastic energy stored in the wire is
View SolutionA spring of spring constant `5 xx 10^(2) `Nm is streched initially by `5 cm` from the unstriched position . Then the work required to streach is further by another `5 cm` is
View SolutionA body is moves along a straight line by a machine dellvering a constant power . The distance moved by the body in time `t` is propertional as
View SolutionA particle move in a straight line with retardation proportional to its displacement its loss of kinectic energy for any displacement `x` is proportional to
View SolutionA uniform chain of length `2m` is kept on a table such that a length of `60 cm` hangas freely from the adge of the table . The table . The total mass of the chain ia `4 kg` What is the work done in pulling the entire the chain the on the table ?
View SolutionA force `barF = (bar5 I + bar3 j + 2 bark ) N` is applied over a particle which displaces it from its original to the point ` bart = (2 bari - bar j ) m `. The work done the particle in joules is
View SolutionA body of mass `m` , accelerates uniform from rest to `v_(1)` in time `t_(1) ` . The instanencoes power delivered to the body as a finction of `t` is
View SolutionA particle is acted upon by a force of constant magnitude which is always is perpendicular to the velocity of the particle , the motion of the particles takes place is a plane it follow that
View SolutionThe block of mass `M` moving on the frictionless horizontal surface collides with the spring constant `k` and compresses it by length `L` . The maximum momention of the block after collision is

View SolutionA spherical ball of mass `20kg` is stationary at the top of a hill of height `100m` , it rolls down a smooth surface to the ground , then climbs up another bill of height of `30 m` and final rolls down to a horizontal base at a height of `20 m` about the ground . The velocity attained by the ball is
View SolutionA body of mass `m` is acceleratad uniformaly from rest to a speed `v` in a time `T` . The instanseous power delivered to the body as a function of time is given by
View SolutionA particle of mass `100 g ` is thrown verically upward with a speed of `5 m//s` . The work done by the of gravity during the time the particle goes up is
View SolutionThe potential energy of a `1 kg` particle free to move along the x- axis is given by `V(x) = ((x^(4))/(4) - x^(2)/(2)) J`
The total mechainical energy of the particle is `2 J` . Then , the maximum speed (in m//s) is
View SolutionA `2kg` block slides on a horizontal floor with the a speed of `4m//s` it strikes a uncompressed spring , and compresses it till the block is motionless . The kinetic friction force is compresses is `15 N` and spring constant is `10000 N//m` . The spring by
View SolutionAs athlete in the olympic ganes cover a distance of `100 m` in `10 s`. Hiskinetic energy can be estrimated to be in the range
View SolutionA block of mass `0.50 kg` is moving with a speed of `2.00 cm^(-1)` can a smooth surface . It strikes another mass of `1.00 kg ` and then they move togather as a single body . The energy less charing the collision is
View SolutionThe potential energy funtions for the force between two along in a distance molecule is approximatily given by
`U(x) = (a)/(x^(12)) - b)/(x^(6)) ` where `a` and `b` are constant and `x` is the distance between the aloms , if the discision energy of the molecale is `D = [U(x = oo) - U` atequlibrium ] , D is
View SolutionThis question has statement `1` and statement `2` . Of the four choice given after the Statement , choose the one that best describe the two Statement .
If the spring `S_(1) `and `S_(2)` of force constant `k_(1)` and `k_(2)` respectively , are streached by the same force , it is found that more work is done on spring `S_(1)` then on spring `S_(2)`
Statement -1: If statement by the same answer work done on `S_(1)` work on `S_(1)` is more then `S_(2)`
Statement - 2 : `k_(1) ltk_(2)`
View SolutionWhen a rubber bandis streched by a distance `x` , if exerts resuring foprce of magnitube `F = ax + bx^(2)` where`a` and `b` are constant . The work in streached the unstreched rubber - band by `L` is
View SolutionA person trying to lose weight by burning fat filts a mass of `10 kg` upto a being of `1m 1000` time . Assume that the potential energy lost each time be lower the mass is dissipated . How much far will be use up considering the work done only when the weight is lifted up ? Far supplies `3.8 xx 10^(7) J` of energy per kg wich is canverted to mechanical energy with `x 20 %` efficiency rate Take ` = 9.8 ms^(-2)`
View Solution
JEE Main And Advanced questions and complete solutions for chapter WORK, ENERGY & POWER of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11