Complete Solutions to illustration. of chapter MEASURES OF CENTRAL TENDENCY MEDIAN AND MODE of Class 11 book with complete answers and questions
| Class 11 | ECONOMICS |
| Chapter | MEASURES OF CENTRAL TENDENCY MEDIAN AND MODE |
| TARUN JAIN & VK OHRI | illustration. |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
The following series show marks in economics of 11 students of Class XI . Find the median marks. `{:("Marks",17,32,35,33,15,21,41,32,11,10,20):}`
View SolutionFind the median of the following series :
`{:("Size",2,3,4,5,6,7,8,9,10),("Frequency",2,3,8,10,12,16,10,8,6):}`
View SolutionFind out median value of the following distribution:
`{:("Wege Rate (Rs.)",0-10,10-20,20-30,30-40,40-50),("Number of Workers", " "22," "38," "46," "35," "20):}`
View SolutionThe following table gives distributionn of marks secured by some stidents :
`{:("Wege Rate (Rs.)",10-20,20-30,30-40,40-50,50-60,60-70,70-80),("Number of Students"," "42," "38," "120," "84," "48," "36," "31):}` Calculate the median marks secured by the students.
View SolutionCalculate median of the following series :
`{:("Wage Rate (Rs.) (less than)",10,20,30,40,50,60,70,80),("Number of Waorkers",15,35,60,84,96,127,198,250):}`
View SolutionCalculate median of the following data :
`{:("Marks",46-50,41-45,36-40,31-35,36-30,21-25,16-20,11-15),("Number of Students"," "5," "11," "22," "35," " 26," "13," "10," "7):}`
View SolutionCalculate median of the following of data :
`{:("Class Interval",0-5,5-10,10-20,20-30,30-50,50-70,70-100),("Number of Students"," "12," "15," "25," "40," "42," "14," "8):}`
View SolutionFind the missing frequency in the following distribution if N=100 and M=30.
`{:("Marks",0-10,10-20,20-30,30-40,40-50,50-60),("Number of Students"," "10," "?," "25," "30," "?," "10):}`
View SolutionFind the missing frequency in the following distribution if N is 60 and median is 40.
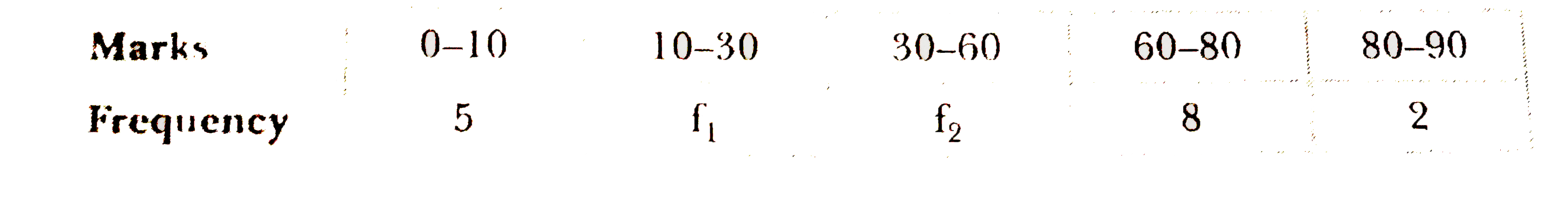
View SolutionDetermine median value of the following series using graphic method :
`{:("Marks",0-5,5-10,10-15,15-20,20-25,25-30,30-35,35-40),("Number of students"," "4," "6," "10," "10," "22," "25," "18," "5):}`
View SolutionFrom the following data , calculate `Q_(1),Q_(3),D_(5)and P_(25)`.
`{:("S.No.",21,15,40,30,26,45,50,54,60,65,70):}`
View SolutionCalcilation `Q_(1),Q_(3),D_(6)and P_(85)` from the following data :
`{:("Size",10,11,12,13,14,15,16,17,18),("Frequency",3,4,5,12,10,7,5,2,1):}`
View SolutionCalculate the values of `Q_(1),Q_(3),D_(8)and P_(85)` - from the following data :
`{:("Wages (Rs.)",0-10,10-20,20-30,30-40,40-50),("Number of Workers"," "22," "38," "46," "35," "19):}`
View SolutionAge of 15 students of a class is reported below find the model age.
`{:("Age (Years)",22,24,17,18,17,19,18,21,20,21,23,22,22,22):}`
View SolutionThe table below presents death rate of population across different coun tries . Find the mode.
`{:("Death Rate",11.1,10.9,10.7,11.1,10.6,11.3,106),("(Per thousand)",10.7,10.6,10.9,10.6,10.5,10.4,10.6):}`
View SolutionFind out mode of the following series :
`{:("Income (Rs.)",110,120,130,140,150,160),("Nunber of Persons"," "2," "4," "8," "10," "5," "4):}`
View SolutionGiven the following data , calculate mode using the grouping technique .
`{:("Size",2,3,4,5,6,7,8,9,10,11,12,13),("Frequency",3,8,10,12,16,14,10,8,17,5,4,1):}`
View SolutionCalculate mode from the following data :
`{:("Class Interval",0-10,10-20,20-30,30-40,40-50),("Frequency"," "2," "5," "7," "5," "2):}`
View SolutionCalculate mode of the following sercies :
`{:("Class Interval",0-5,5-10,10-15,15-20,20-25,25-30,30-35),("Frequency"," "1," "2," "10," "4," "10," "9," "2):}`
View Solution`{:("Class Interval",0-4,4-8,8-12,12-14,14-16,16-20,20-24,24-26,26-32,32-34,34-40,40-44,44-48),("Frequency"," "2," "4," "7," "5," "8," "3" "," "2," "1," "13," "5," "3," "3," "9):}`
View SolutionCaculate mode of the following data :
`{:("Marks",0-5,5-10,10-20,20-40,40-60,60-80,80-90,90-100),("Number of Students"," "5," "7," "9," "25" "," "30," "24," "8," "6):}`
View SolutionCalculate mode of the following sercies:
`{:("Class Interval",10-19,20-29,30-39,40-49,50-59,60-69,70-79),("Frequency"," "10," "12," "18," "30," "16," "6," "8):}`
View SolutionCalculate mode , given the following data set :
`{:("Mid - value",15,25,35,45,55,65,75,85),("Frequency",5,8,12,16,28,15,3,2):}`
View SolutionFind out mode of the following series :
`{:("Wages (Rs.) less than",200,300,400,500,600,700,800,900),("Number of Workers",5,18,38,70,90,95,98,100):}`
View SolutionCalculate mode of a series , the mean and median values of which are 16 cm and 20 cm respectively.
View SolutionCalculate mode of the following series , using the Graphic Technique :
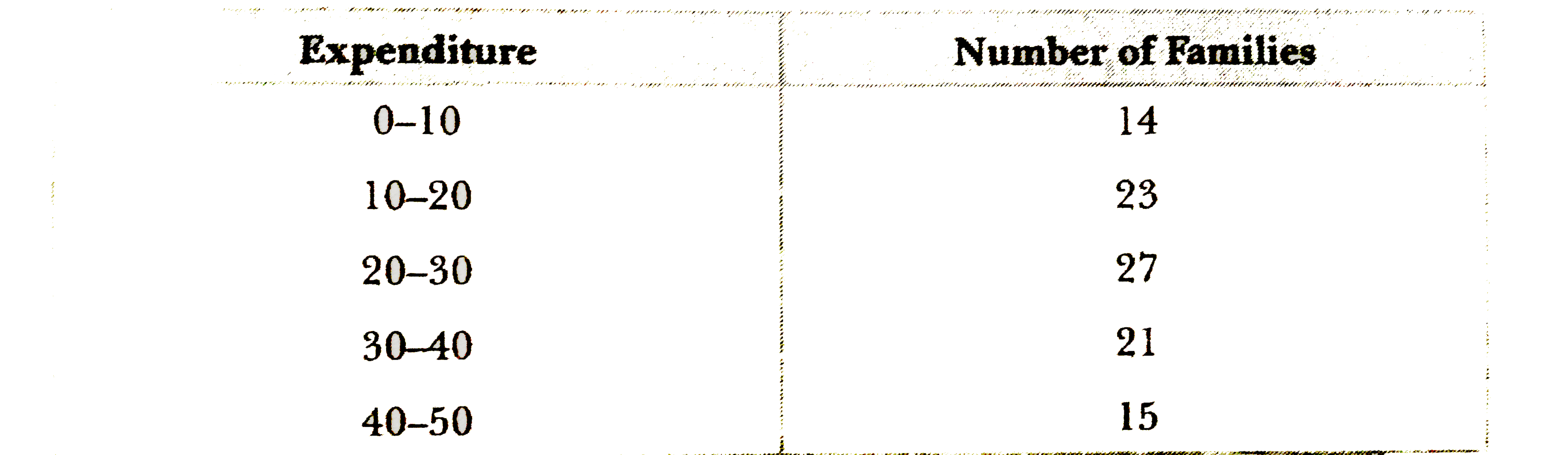
View SolutionIf in an asymmetrical distribution , median is 280 and mean is 310 , what will be the mode ?
View Solution
illustration. questions and complete solutions for chapter MEASURES OF CENTRAL TENDENCY MEDIAN AND MODE of VK GLOBAL PUBLICATION ECONOMICS (HINGLISH) of Class 11