Complete Solutions to Exercise of chapter Some New Pattern Problems of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | Some New Pattern Problems |
| A DAS GUPTA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The envelope of the family of straight lines whose sum of intercepts on the axes is 4 is
View SolutionThe envelope of the family of tangents to the curve `y^2=x` is
View SolutionThe evolute of the curve `x^2=4y` is
View SolutionThe area bounded by the curve `y= f(x)` and the lines `x=0, y=0` and `x=t`, lies in the interval
View SolutionThe radius of curvature of the curve `y^2=4x` at the point `(1, 2)` is
View SolutionIf `e_1` is the eccentricity of the conic `9x^2+4y^2=36\ a n d\ e_2` is the eccentricity of the conic `9x^2-4y^2=36` then `e1 2-e2 2=2` b. `e2 2-e1 2=2` c. `2<3 2 2-3 1 2<3` d. `e2 2-e1 2>3`
View Solution` int _(-pi//2)^(pi//2) sin | x | dx ` is equal to
View Solution`int (sin(1/x)cos^3(1/x))/x^2dx` is equal to
View SolutionIf `f''(x) lt 0 AA x in (a,b)` and `(c, f(c))` is a point lying on the curve `y =f(x)`, where `a < c < b` and for that value of `c`, `f(c)` has a maximum then `f'(c)` equals
View SolutionThe family of parabolas with a common vertex at the origin whose foci are on the x-axis and the directrices are parallel to the y-axis can have the equation (a being a parameter)
View SolutionThe orthogonal trajectory of the family of parabolas `y^2 =4ax` is
View SolutionThe curve passing through the point `(1, 2)` that cuts each member of the family of parabolas `y^2= 4ax` orthogonally is
View SolutionThe general solution of the equation `((d^3y)/(dx^3)) - 7 ((d^2y)/(dx^2)) +16 (dy)/(dx) -12 y=0`
View SolutionFind the differential equation for which the following value of `y` is the general solution: `y=(c_1 cos x + c_2 sin x) e^(-x) + c_3 e^x`
View SolutionThe general solution of the equation `(d^3 y)/ (dx^3) +y=0` is
View SolutionThe value of `|U|` where `U= [(2,3,4),(3,4,5),(4,5,6)]`
View Solutionshow that matrix `A = [(3,4),(1,2)]` satisfies the equation `A^2-5A+2I=0`
View SolutionThe sum of the elements of the product `[3, 2,0] and [(3),(2), (0)]` is
View SolutionThe rank of matrix `[(x, -1, 0), (0, x, -1), (-1, 0,x)]` is `2` then value of `x` is:
View SolutionOne of the eigenvalues of A is where `A= [(2,5),(7,4)]`
View SolutionThe denary number 43125 in the scale of 6 will be represented by
View SolutionThe sum of the numbers `2053` and `412` in the scale of seven is
View SolutionThe product of the numbers 5623 and 6 in the scale of eight is
View SolutionWhich of thefollowing is true?
View SolutionLet `a = b (mod n), a'= b' (mod n)` and `d, m in N. Then which of the following need not be true?
View SolutionIf `5x = 3(mod 7)` then find `x`
View SolutionThe value of `lambda` for which the equation `lambda^2 - 4lambda + 3+ (lambda^2 + lambda -2)x + 6x^2 - 5x^3 =0` will have two roots equal to zero is
View SolutionThe value of `(lambda, mu)` for which `(lambda - mu) x^3 - (lambda - 2) x^2 -3x +7=0` will have two infinite roots is
View SolutionThe combined equation of asymptotes to the hyperbola `x^2 + 4xy + 3y^2 +4x-3y +1=0` are
View Solution`17^22 - 1` is a multiple of
View SolutionThe highest power of 7 which divides 1000 ! is
View SolutionThe equation of conjugate hyperbola of `x^2/8 - 3y^2/8 =1`
View SolutionThe parabola circumscribing `/_\ABC` and passing through the point `(4, 4)` has the focus
View SolutionThe parabola circumscribing `/_\ABC{(0,0), (4,4), (4,-4)}` and passing through the point `(4, 4)` has the latus rectum
View SolutionIf `A = (2, (3sqrt3/2))` then coordinates of C taken mirror image along x=0 is
View SolutionIf the equation of the diameter AB is `x = y` then the equation of the conjugate diameter CD will be
View SolutionThe equations of the line QR are where `Q (3, 6, 3) , R(18, 43, 13)`
View SolutionThe distance of the centre of the sphere `x^2 + y^2 + z^2 - 2x - 4y = 0` from the origin is
View SolutionThe radius of the circle of intersection of the sphere `x^2 +y^2 +z^2=9` by the plane `3x +4y +5z=5` is
View SolutionThe area of the sphere `x^2 + y^2 + z^ 2 = 25` is
View SolutionIf `P(u_i)) oo i` , where `i = 1, 2, 3, . . ., n`then `lim_(nrarrw) P(w)` is equal to
View SolutionThere are `n` urns each containing `(n + 1)` balls such that the `i^(th)` urn contains `i` white balls and `(n + 1 - i)` red balls. Let `u_i` be the event of selecting `i^(th)` urn, `i = 1,2,3,.... , n` and `w` denotes the event of getting a white balls. If `P(u_i) = c` where `c` is a constant, then `P(u_n/w )` is equal
View SolutionThe set of values of `p inR` for which ` x^2 +px+ 1/4 (p+2)ge 0` for all`x in R` is
View SolutionThe set of values of `p in R` for which the equation `x^2 +px+ 1/4 (p+2)= 0` will have real roots is
View SolutionIf p is chosen at random from the interval `[0, 6]` then the probability that the roots of the equation `x^2 +px+ 1/4 (p+2)= 0` will be real is
View SolutionA bag contain 2 white balls and 1 red balls. The experiment is done 10 times. The probability that a white ball is drawn exactly 5 times is
View SolutionA bag contain 2 white balls and 1 red balls. The experiment is done 10 times. The probability that a white ball is drawn exactly 5 times is
View SolutionIf `n^(2)+2n -8` is a prime number where `n in N ` then n is
View SolutionIf z is a complex number, then `| 3z -1| = 3 | z-2|` represents
View SolutionIn Q.no. 88, if z be any point in `A frown B frown C` and `omega` be any point satisfying `|omega-2-i| lt 3`. Then, `|z|-|omega|+3` lies between
View SolutionWhich of the following is true?
View SolutionWhich of the following is true?
View SolutionConsider the function f : `(-oo , oo) to (-oo , oo)` defined by f(x) = `(x^(2) - ax + 1)/(x^(2) + ax + 1) , 0 lt a lt 2`
Let `g (x) = underset(0) overset(e^(x))(int) (f'(t))/(1 + t^(2)) `dt
Which of the following is true ?
View SolutionConsider the line
`L1=(x+1)/3=(y+2)/1=(z+1)/2`
`L2=(x-2)/1=(y+2)/2=(z-3)/3`
The shortest distance between `L_1` and `L_2` is
View SolutionConsider the line
`L1=(x+1)/3=(y+2)/1=(z+1)/2`
`L2=(x-2)/1=(y+2)/2=(z-3)/3`
The shortest distance between `L_1` and `L_2` is
View Solutioncosider the lines,
`L1=(x+1)/3=(y+2)/1=(z+2)/2`
`L2=(x-2)/1=(y+2)/2=(z-3)/3`
The distance of the point `(1, 1, 1)` from the plane passing through the point `(-1, -2, -1)` and whose normal is perpendicular to both the lines `L_1` and `L_2` is
View SolutionConsider the function defined implicitly by the equation `y^3-3y+x=0` on various intervals in the real line. If `x in (-oo,-2) uu (2,oo)`, the equation implicitly defines a unique real-valued defferentiable function `y=f(x)`. If `x in (-2,2)`, the equation implicitly defines a unique real-valud diferentiable function `y-g(x)` satisfying `g_(0)=0`.
If `f(-10sqrt2)=2sqrt(2)`, then `f"(-10sqrt(2))` is equal to
View SolutionThe area of the region bounded by the curve `y= f( x )`, x-axis, and the lines `x=a` and `x=b` where `-oo lt a lt b lt -2` is
View Solution`int_(-1)^1 g'(x) dx=`
View SolutionThe equation of the circle C with center at `(sqrt3,1)` is
View SolutionThe number of 2 `x` 2 matrices A such that all entries are either 1 or 0 is
View SolutionLet A be the set of all `3xx3` symmetric matrices all of whose either 0 or 1. Five of these entries are 1 and four of them are 0.
The number of matrices A in A for which the system of linear equations
`A[(x),(y),(z)]=[(1),(0),(0)]`
has a unique solution is
View SolutionLet A be the set of all `3xx3` symmetric matrices all of whose either 0 or 1. Five of these entries are 1 and four of them are 0.
The number of matrices A in A for which the system of linear equations
`A[(x),(y),(z)]=[(1),(0),(0)]`
is inconsistent is
View SolutionA fair die is tossed repeatedly until a 6 is obtained. Let X denote the number of tosses required.
The probability that `X=3` equals
View SolutionA fair die is tossed repeated until a six is obtained. Let X denote the number of tosses required.
The probability that `X ge 3` is
View SolutionA fair die is tossed repeatedly until a six obtained. Let X denote the number of tosses required.
The conditional probability that `X ge 6` given `X gt 3` equals
View SolutionEquation of the common tangent to the circle `x^(2)+y^(2)=50` and the parabola `y^(2)=40x` can be
View SolutionIf the events A and B are mutually exclusive events such that P(A) = `(3x + 1)/(3)` and P(B) = `(1 - x)/(4)`, then the set of possible real values of x lies in the interval
View SolutionLet s be the sum of all distinct real roots of f(x) and let `t=mod(s)`The area bounded by the curve `y= f(x)` and the lines `x=0, y=0` and `x=t`, lies in the interval
View SolutionTangents are drawn from the point P(3,4) to be the ellipse `x^2/9+y^2/4=1` touching the ellipse at A and B . Then the coordinates of A and B are.
View SolutionThe tangents are drawn from the point `P(3,4)` to the ellipse `x^2/9+y^2/4=1` touching the ellipse at points `A` and `B`. The orthocenter of the triangle PAB is
View SolutionTangents are drawn from the point P(3,4) to the ellipse `x^2/9+y^2/4=1` touching the ellipse at the point A and B then the equation of the locus of the point whose distances from the point P and the line AB are equal, is
View SolutionMatch the following (more than one may match with the same).
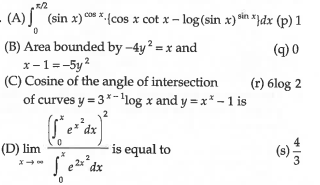
View SolutionMatch the following (more than one may match with the same).

View SolutionLet `aa n db` be the roots of the equation `x^2-10 c x-11 d=0` and those of `x^2-10 a x-11 b=0a r ec ,ddot` then find the value of `a+b+c+ddotw h e na!=b!=c!=ddot`
View SolutionComplete the following statements.
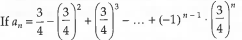 and `b_n=1-a_n` then the smallest natural number `n_0`, such that `b_n > a_n Vnt n> n_0` is
and `b_n=1-a_n` then the smallest natural number `n_0`, such that `b_n > a_n Vnt n> n_0` is
View SolutionIf f(x) is a twice differentiable function such that f(a)=0, f(b)=2, f(c)=-1,f(d)=2, f(e)=0 where a < b < c < d e, then the minimum number of zeroes of `g(x) = f'(x)^2+f''(x)f(x)` in the interval [a, e] is
View SolutionConsider the planes `3x-6y-2z=15a n d2x+y-2z=5.` Statement 1:The parametric equations of the line intersection of the given planes are `x=3+14 t ,y=2t ,z=15 tdot` Statement 2: The vector `14 hat i+2 hat j+15 hat k` is parallel to the line of intersection of the given planes.
View SolutionLet the vectors `vec(PQ),vec(QR),vec(RS), vec(ST), vec(TU)` and `vec(UP)` represent the sides of a regular hexagon.
Statement I:`vec(PQ) xx (vec(RS) + vec(ST)) ne vec0`
Statement II: `vec(PQ) xx vec(RS) = vec0` and `vec(PQ) xx vec(RS) = vec0` and `vec(PQ) xx vec(ST) ne vec0`
For the following question, choose the correct answer from the codes (A), (B) , (C) and (D) defined as follows:
View SolutionTangents are drawn from the point (17, 7) to the circle `x^2+y^2=169`, Statement I The tangents are mutually perpendicular Statement, lls The locus of the points frorn which mutually perpendicular tangents can be drawn to the given circle is `x^2 +y^2=338` (a) Statement I is correct, Statement II is correct; Statement II is a correct explanation for Statementl (b( Statement I is correct, Statement I| is correct Statement II is not a correct explanation for Statementl (c)Statement I is correct, Statement II is incorrect (d) Statement I is incorrect, Statement II is correct
View SolutionThe lines `L_(1) : y - x = 0` and `L_(2) : 2x + y = 0` intersect the line `L_(3) : y + 2 = 0` at P and Q respectively . The bisectors of the acute angle between `L_(1)` and `L_(2)` intersect `L_(3)` at R .
Statement 1 : The ratio PR : RQ equals `2sqrt2 : sqrt5`
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View SolutionLet C be the locus of a point the sum of whose distances from the points `S(sqrt3,0) and S'(-sqrt3,0) " is " 4.`
Statement-1: The curve C cuts off intercept `2sqrt3` from the line 2y-1=0
Statement-2: The equation of the centre C is `x^(2)+ 8y^(2)=5`
View SolutionLet F(x) be an indefinite integral of `sin^(2)x`
Statement I The function F(x) satisfies `F(x+pi)=F(x)` for all real x.
Because
Statement II `sin^(2)(x+pi)=sin^(2)x,` for all real x.
View Solutionlet `f(x)=2+cosx` for all real x Statement 1: For each real t, there exists a pointc in `[t,t+pi]` such that `f'(c)=0` Because statement 2: `f(t)=f(t+2pi)` for each real t
View SolutionAssertion- Reason Type Question:
STATEMENT -1: `1*3*5* ….*(2n-1) gt n^n, n in N` because
STATEMENT -2: the sum of the first n natural numbers is equal to `n^2`.
View SolutionLet `(1 + x)^(36) = a_(0) +a_(1) x + a_(2) x^(2) +...+ a_(36)x^(36)`. Then
Statememt-1: `a_(0) +a_(3) +a_(6) +…+a_(36)= (2)/(3) (2^(36) +1)`
Statement-2: `a_(0) + a_(2) +a_(4) +…+ a_(36) = 2^(35)`
View SolutionThe vlaue of `((5050)underset(0)overset(1)int(1-x^(50))^(100)dx)/(underset(0)overset(1)int (1-x^(50))^(100)dx)`, is
View SolutionIn `!ABC` it is given that a:b:c = cos A:cos B:cos C
Statement-1: `!ABC` is equilateral.
Statement-2: cosA`=(b^(2)+c^(2)-a^(2))/(2bc),cosB=(c^(2)+a^(2)-b^(2))/(2ac),cosC=(a^(2)+b^(2)-c^(2))/(2ab)`
View SolutionLet `H_1, H_2,..., H_n` be mutually exclusive events with `P (H_i) > 0, i = 1, 2,.......... n.` Let `E` be any other event with `0 < P (E)` Statement I `P(H_i|E) > P(E|H_i .P(H_i)` for `i=1,2,.......,n` statement II `sum_(i=1)^n P(H_i)=1`
View SolutionLet `Aa n dB` b e two independent events. Statement 1: If `(A)=0. 3a n dP(Auu B )=0. 8 ,t h e nP(B)` is 2/7. Statement 2: `P(E)=1-P(E),w h e r eE` is any event.
View SolutionThe equations of two straight lines are
`(x-1)/2=(y+3)/1=(z-2)/(-3)` and `(x-2)/1=(y-1)/(-3)=(z+3)/2`
Statement 1: The given lines are coplanar.
Statement 2: The equations
`2r-s=1`
`r+3s=4`
`3r+2s=5`
are consistent.
View SolutionAssertion- Reason Type Question:
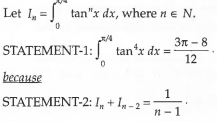
View SolutionStatement-1: The cubic equation `4x^(3) - 15x^(2)+14x-5 = 0` has a root in the internal (2, 3).
Statement-2: If f(x) is a polynomial equation which has two real roots `alpha, beta (alpha lt beta)`, then f(x) = 0 will have a root `gamma such that `alpha lt gamma lt beta`.
View SolutionConsider, `L_(1) : 2x + 3y + p – 3 = 0 , L_(2) : 2x + 3y + p + 3 = 0`, where p is a real number, and `C : x^(2)+y^(2)+6x–10y+30=0`
Statement-I : If line `L_(1)` is a chord of circle C, then line `L_(2)` is not always a diameter of circle C.
and
Statement-II : If line `L_(1)` is a diameter of circle C, then line `L_(2)` is not a chord of circle C.
View SolutionLet a,b,c,p,q be the real numbers. Suppose `alpha,beta` are the roots of the equation `x^2 +px +q =0` and `alpha, beta/2` are the roots of the equation `ax^2 +bx +c =0` where `beta^2 !in {-1,0,1}.`
View SolutionFor the following question, choose the correct answer from the codes (a),(b),( c ) and (d) follows
Let a solution y=y(x) of the differential equation `xsqrt(x^(2)-1)dy-ysqrt(y^(2)-1)dx=0` satisfy y(2)=`(2)/(sqrt3)`
Statement I y(x) = sec `(sec^(-1)x-(pi)/(6))` and
Statement II y(x) is given by `(1)/(2)=(2sqrt3)/(x)-sqrt(1-(1)/(x^(2)))`
View SolutionConsider three planes `P_1:x-y+z=1, P_2:x+y-z=-1,P_3,x-3y+3z=2` Let `L_1,L_2,L_3` be the lines of intersection of the planes `P_2 and P_3 and P-1,P_1 and P_2,` respectively.
View SolutionConsider the system of equations
x-2y+3z=-1
-x+y-2z=k
x-3y+4z=1
Statement -1 The system of equation has no solutions for `k ne 3`.
statement -2 The determinant `|{:(1,3,-1),(-1,-2,k),(1,4,1):}| ne0, "for"" " kne3.`
View SolutionConsider the system of equations ax + by = 0; cx + dy = 0, where `a, b, c, d in {0,1}`)STATEMENT-1: The probability that the system of equations has a unique solution is 3/8 STATEMENT-2: The probability that the system of equations has a solution is 1
View SolutionLet `f` and `g` be real valued functions defined on interval `(-1,\ 1)` such that `g"(x)` is continuous, `g(0)!=0` , `g'(0)=0,` `g"(0)!=0` , and `f(x)=g(x)sinx` . Statement-1 : `("Lim")_(x->0)[g(x)cotx-g(0)"c o s e c"x]=f"(0)` and Statement-2 : `f'(0)=g(0)`
View Solution
Exercise questions and complete solutions for chapter Some New Pattern Problems of BHARATI BHAWAN MATHS (HINGLISH) of Class 12