Complete Solutions to Motion Of Charged Particle In Magnetic Field of chapter SOURCE AND EFFECT OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCE AND EFFECT OF MAGNETIC FIELD |
| A2Z | Motion Of Charged Particle In Magnetic Field |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA particle of charge q and mass `m` is moving along the x-axis with a velocity `v` and enters a region of electric field `E` and magnetic field `B` as shown in figures below. For which figure the net force on the charge may be zero?
View SolutionA uniform magnetic field `B` and a uniform electric field `E` act in a common region. An electron is entering this region of space. The correct arrangement for it to escape undeviated is
View SolutionIf a proton is projected in a direction perpendicular to a uniform magnetic field with velocity `v` and and electron is projected along the line of force, what will happen to proton and electron?
View SolutionAn electron is travelling horizontally towards east. A magnetic field in vertically downward direction exerts a force on the electron along
View SolutionA homogenous electric field `E` and a uniform magnetic field `vecB` are pointing in the same direction. A proton is projected with its velocity parallel to `vecE`. It will
View SolutionA very long straight wire carries a current I. At the instant when a charge `+Q` at point `P` has velocity `vecV`, as shown, the force on the charge is
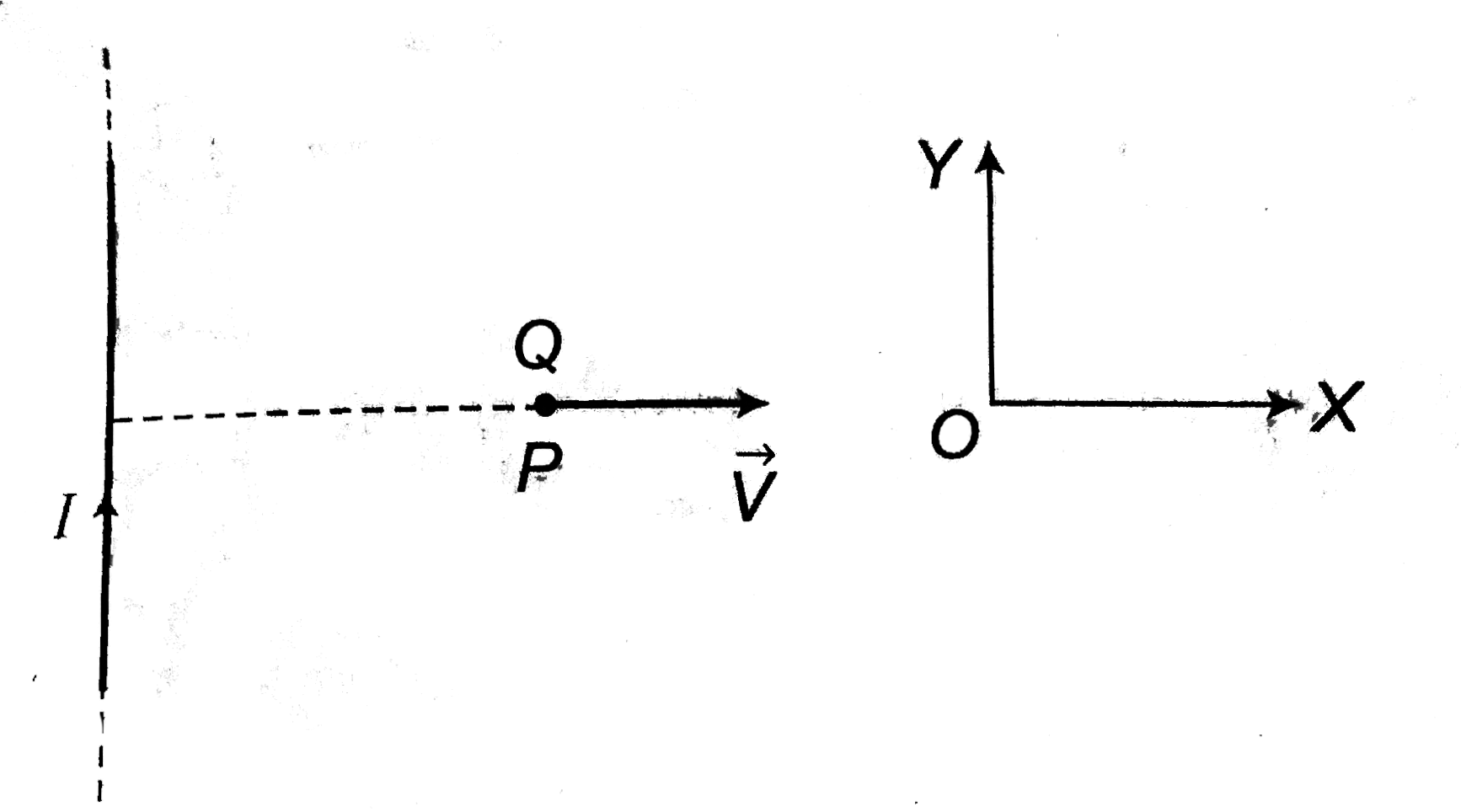
View SolutionAn electron and a proton have equal kinetic energies. They enter in a magnetic field perpendicularly, then
View SolutionA proton (or charged particle) moving with velocity `v` is acted upon by electric field `E` and magnetic field `B`. The proton will move undeflected if
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionA charged particle moves with velocity `vecv` in a uniform magnetic field `vecB`. The magnetic force experienced by the particle is
View SolutionA potential difference of `600 volts` is applied across the plates of a parallel plate consenser . The separation between the plates is `3mm`. An electron projected vertically, parallel to the plates , with a velocity of `2 xx 10^(6) m//sec` moves underflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. ( Neglect the edge effects). ( Charge of the electron `= -1.6xx10^(-19) coulomb)
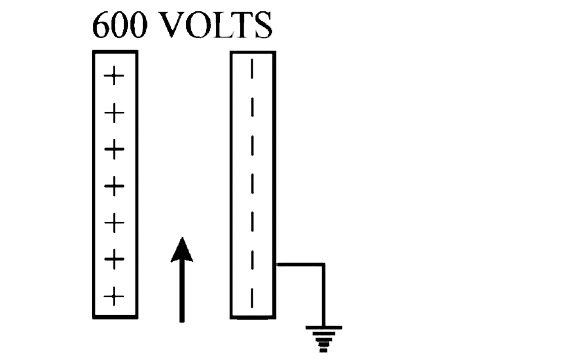
View SolutionA proton and an `alpha-`particle enter a uniform magnetic field moving with the same speed. If the proton takes `25 mu s` to make 5 revolutions, then the periodic time for the `alpha-` particle would be
View SolutionA proton (mass m and charge `+e`) and an `alpha`-particle (mass `4` m and charge `+2e`) are projected with the same kinetic energy at right angles to the uniform magnetic field. Which one of the following statements will be true?
View SolutionA proton of mass m and charge `+e` is moving in a circular orbit in a magnetic field with energy `1 MeV`. What should be the energy of `alpha`-particle (mass=`4m` and charge=`+2e`), so that it can revolve in the path of same radius?
View SolutionA deuteron of kinetic energy `50` keV is desvribing a circular orbit of radius `0.5` meter in a plane perpendicular to magnetic field `vecB`. The kinetic energy of the proton that describes a circular orbit of radius `0.5` meter in the same plane with the same `vecB` is
View SolutionIf a particle of charge `10^(-12)` coulomb moving along the `hat(x)`-direction with a velocity `10^(5)m//s` experiences a force of `10^(-10)` newton in `hat(y)`-direction due to magnetic field. Then the minimum magnetic field is
View SolutionAn electron and a proton enter region of uniform magnetic field in a direction at right angles to the field with the same kinetic energy. They describe circular paths of radius `r_(e)` and `r_(p)` respectively. Then
View SolutionAn electron moving with a speed u along the positive x-axis at `y=0` enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionTwo identical particles having the same mass m and charges +q and -q separated by a distance d enter a uniform magnetic field B directed perpendicular to paper inwards with speeds `v_1 and v_2` as shown in Fig. The particles will not collide if

View SolutionTwo very long straight parallel wires carry steady currents `i` and `2i` in opposite directions. The distance between the wires is `d`. At a certain instant of time a point charge `q` is at a point equidistant from the two wires in the plane of the wires. Its instantaneous velocity `vecv` is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on t he charge at this instant is
View SolutionA charged particle enters a uniform magnetic field with velocity vector at angle of `45^@` with the magnetic field. The pitch of the helical path followed by the particle is p. the radius of the helix will be
View SolutionA proton of mass `1.67xx10^(-27)kg` and charge `1.6xx10^(-19)c` is projected with a speed of `2xx10^(6)m//s` at an angle of `60^(@)` to the x-axis. If a uniform magnetic field of `0.104` Tesla is applied along Y-axis, the path of proton is
View SolutionA proton and a deuteron both having the same kinetic energy, enter perpendicularly into a uniform magnetic field `B`. For motion of proton and deuteron on circular path or radius `R_(p)` and `R_(d)` respectively, the correct statement is
View SolutionA proton and an electron both moving with the same velocity v enter into a region of magnetic field directed perpendicular to the velocity of the particles. They will now move in cirular orbits such that
View SolutionThe charge on a particle `Y` is double the charge on particle `X`. These two particles `X` and `Y` after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii `R_(1)` and `R_(2)` respectively. The ratio of the mass of `X` to that of `Y` is
View SolutionA particle of charge `q` and mass `m` moving with a velocity `v` along the x-axis enters the region `xgt0` with uniform magnetic field `B` along the `hatk` direction. The particle will penetrate in this region in the `x`-direction upto a distance `d` equal to
View SolutionA proton , a deuteron and `alpha )`- particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field . If ` r_(p), r_(d) , and r_(alpha)` denote respectively the radii of the trajectories of these particles , then
View SolutionMaximum kinetic energy of the positive ion in the cyclotron is
View SolutionTwo particles `A and B` of masses ` m_(A) and m_(B)` respectively and having the same charge are moving in a plane . The speeds of the particles are ` v_(A) and v_(B)` respectively and the trajectories are as shown in the figure. Then
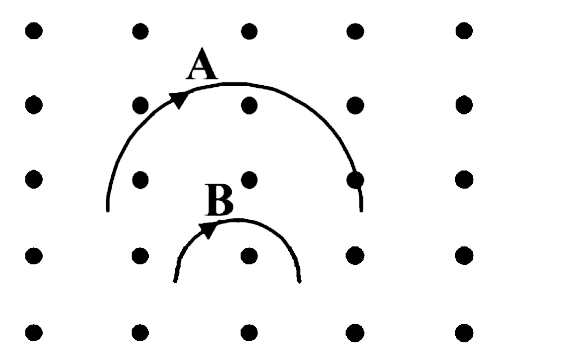
View SolutionA proton and an alpha particle are separately projected in a region where a uniform magnetic field exists. Their initial velocities are perpendicular to direction of magnetic field. If both the particles move around magnetic field in circles of equal radii, the ratio of momentum of proton to alpha particle `(p_(p)/(p_(alpha)))` is
View SolutionA particle of mass `0.6g` and having charge of `25 nC` is moving horizontally with a uniform velocity `1.2xx10^(4)ms^(-1)` in a uniform magnetic field, then the value of the magnetic induction is `(g=10ms^(-2))`
View SolutionMixed `He^(+)` and `O^(2+)` ions (mass of `He^(+)`=4 amu and that of `O^(2+)=16` amu) beam passes a region of constant perpendicular magnetic field. If kinetic energy of all the ions is same then
View SolutionA proton of energy `8 eV` is moving in a circular path in a uniform magnetic field. The energy of an alpha particle moving in the same magnetic field and along the same path will be
View SolutionAn electron, a proton, a deuteron and an alpha particle, each having the same speed are in a region of constant magnetic field perpendicular to the direction of the velocities of the particles. The radius of the circular orbits of these particles are respectively `R_(e), R_(p), R_(d)` and `R_(alpha)` It follows that
View SolutionAn electron moves in a circular orbit with a uniform speed `v`.It produces a magnetic field `B` at the centre of the circle. The radius of the circle is proportional to
View SolutionAn electron (mass `=9.1xx10^(-31)kg`, charge `=1.6xx10^(-19)C`) experiences no deflection if subjected to an electric field of `3.2`x`10^(5)V/m``, and a magnetic fields of `2.0xx10^(-3)Wb/m^(2)`. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
View SolutionAn `(alpha)`-particle and a proton are both simultaneously projected in opposite direction into a region of constant magnetic field perpendicular to the direction of the field. After some time it is found that the velocity of the `(alpha)`-particle has changed in a direction by `45^(@)`. Then at this time, the angle between velocity vectors of `(alpha)`-particle and proton is
View SolutionAn electron gun ejects electrons at an angle of `45^(@)` with magnetic field boundary as shown in Fig. Find the angular deviation of electrons as it comes out of field.

View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point 2a, `b//2`, 0 its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View SolutionA particle of specific charge `q//m = (pi) C//kg` is projected from the origin towards positive x-axis with a velocity of `10 m//s` in a uniform magnetic field `vec(B) = -2 hat K` Tesla. The velocity `vec V` of the particle after time `t =1//6` s will be
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field `vec E = E_0 hat i and vec B = B_0 hat i` with a velocity `vec v = v_0 hat j`. The speed of the particle will become `2v_0` after a time.
View SolutionA charged particle of specific charge (charge/mass) `alpha` released from origin at time `t=0` with velocity `vec v = v_0 (hat i + hat j)` in uniform magnetic field `vec B = B_0 hat i.` Coordinates of the particle at time `t= pi//(B_0 alpha)` are
View SolutionAn electron is accelerated from rest through a potential difference V. This electron experiences a force F in a uniform magnetic field. On increasing the potential difference to V', the force experienced by the electron in the same magnetic field becomes 2F. Then, the ratio `(V'//V)` is equal to
View SolutionA charged particle enters into a uniform magnetic field with velocity `v_(0)` perpendicular to it , the length of magnetic field is `x=sqrt(3)/(2)R`, where `R` is the radius of the circular path of the particle in the field .The magnitude of change in velocity of the particle when it comes out of the field is
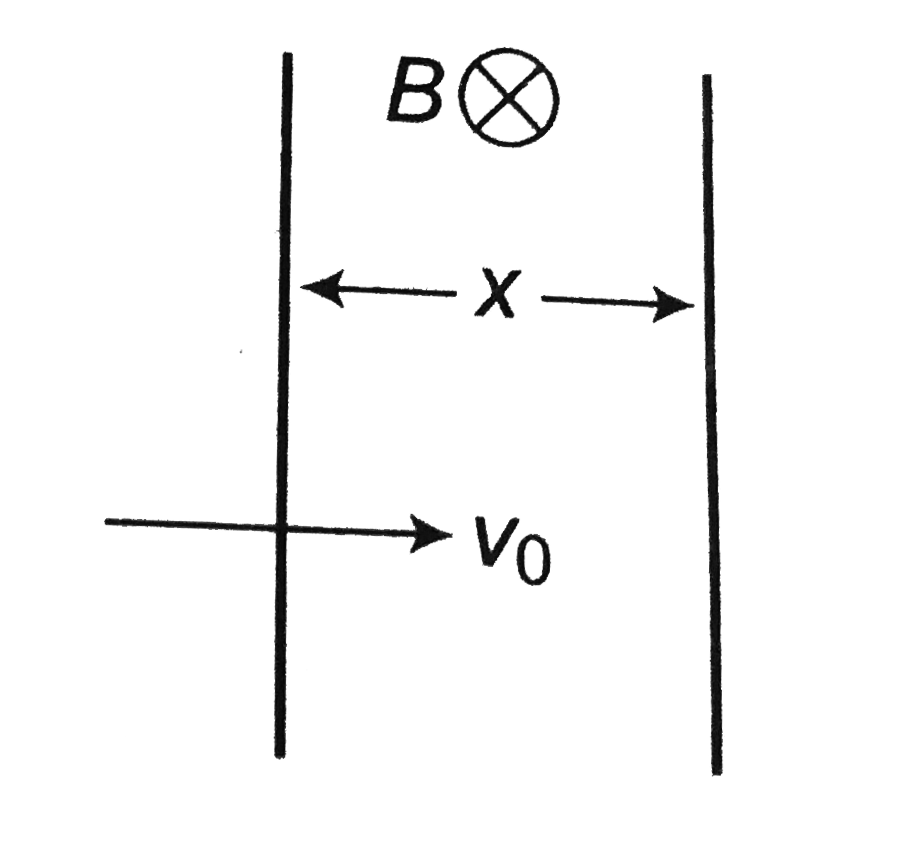
View SolutionA particle of charge `Q` moving with kinetic energy `K` enters a zone of uniform magnetic field `B` along normal to `A_(1)B_(1)` as shown satisfying the condition `dgt(2K)/(QvB)` where `v` is the velocity of the particle .What will be tha angle of deflection in crossing the field at the centra of the curve followed by the particle in the field, if `K=QvBb` ? (`b`=radius of the circle in which the particle rotates)

View SolutionA particle with charge `q`, moving with a momentum `p`, enters a uniform magnetic field normally. The magnetic field has magnitude `B` and is confined to a region of width `d`, where `dlt(p)/(Bq)`. If the particle is deflected by an angle `theta` in crossing the field then

View SolutionA proton accelerated by a potential difference `V = 500 kV` flies through a uniform transverse magnetic filed the induction `B = 0.54 T`. The field occupies a region of space `d = 10 cm` in thickness (Fig). Find the angle `alpha` through which the proton deviates from the initial direction of its motion.

View SolutionA particle of the mass ` m ` and charge ` q` moves with a constant velocity `v` along the positive ` x`- direction . It enters a region containing a uniform magnetic field `B` directed along the minimum value of `v` required so that the particle can just enter the region ` xgtb` is
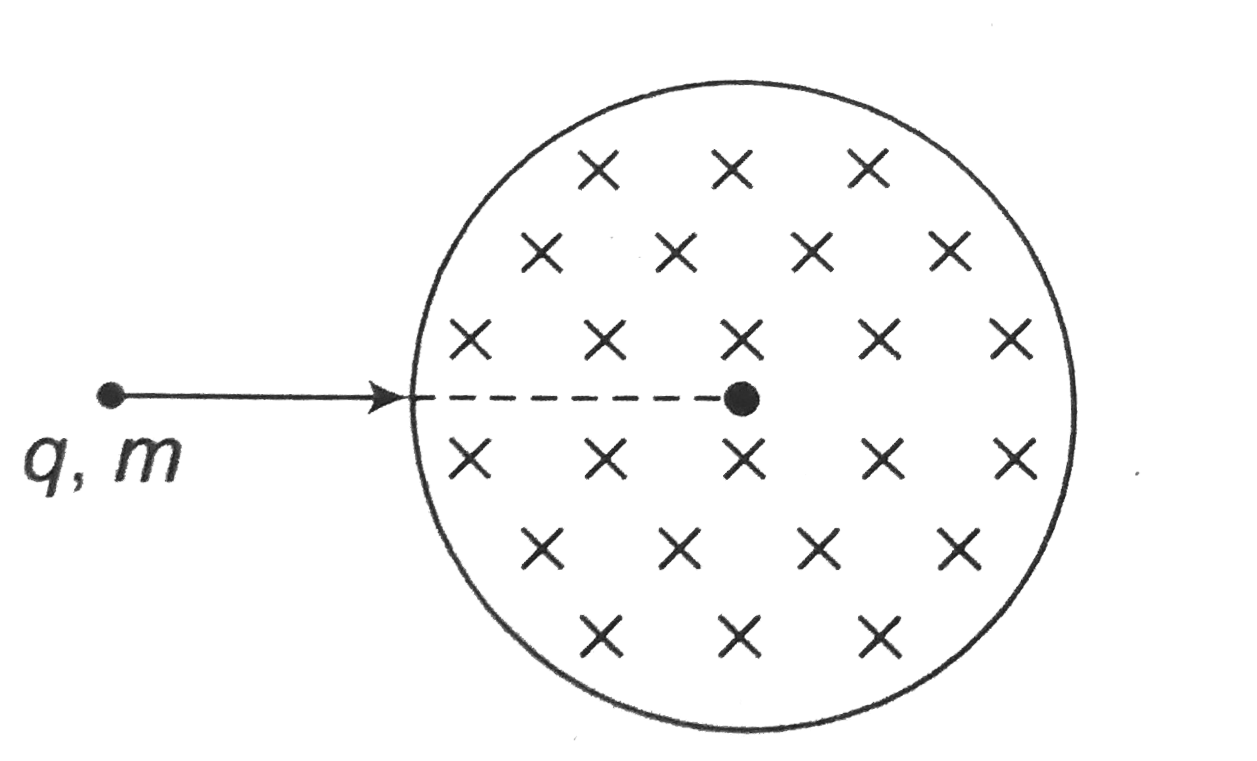
View SolutionA particle having mass `m`, charge `q` enters a cylindrical region having uniform magnetic field `B` in the inward direction as shown. If the particle is deviated by `60^(@)` as it emerges out of the field then what is the time spent by it in the field?
View SolutionA particle of mass `m` having negative charge `-q` is projected at an angle `theta` with `x`-axis. There exists uniform electric field `E` and a unifrom magnetic field `B` along `x`-axis. The particle will return to its intial point once if (`n` is some integer)

View SolutionA charged particle is projected with a certain velocity between the plates with opposites charges. The magnetic field is also applied between the plates so that the particle moves undeflected and hits the plate `A`. The force experienced by the plate is `F_(1)`. Now if the particle is projected with double of the initial velocity with smaller conditions, the force experienced by the plate is `F_(1)//F_(2)` is :

View SolutionA particle of charge per unit mass `alpha` is released from origin with a velocity `vecv=v_(0)hati` uniform magnetic field `vecB=-B_(0)hatk`. If the particle passes through `(0,y,0)`, then `y` is equal to
View SolutionFor a positively charged particle moving in a `x-y` plane initially along the `x-axis` , there is a sudden change in its path due to the presence of electric and//or magnetic fields beyond `p` . The curved path is shown in the ` x- y `plane and is found to be non - circular. Which one of the following combinations is possible ?
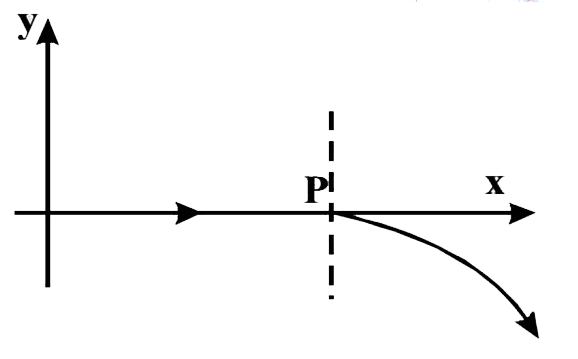
View Solution
Motion Of Charged Particle In Magnetic Field questions and complete solutions for chapter SOURCE AND EFFECT OF MAGNETIC FIELD of A2Z PHYSICS (HINGLISH) of Class 12
All Exercises from A2Z Class 12 PHYSICS SOURCE AND EFFECT OF MAGNETIC FIELD
- AIIMS Questions
- AIPMTNEET Questions
- Assertion- Reason
- Force On A Current Carrying Conductor In Magnetic Field
- Magnetic Dipole
- Magnetic Field Due To Circular Arc
- Magnetic Field Due To Current
- Motion Of Charged Particle In Magnetic Field
- Problems Based On Mixed Concepts
- Section B - Assertion Reasoning
- Section D - Chapter End Test