Complete Solutions to Magnetic Field Due To Circular Arc of chapter SOURCE AND EFFECT OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCE AND EFFECT OF MAGNETIC FIELD |
| A2Z | Magnetic Field Due To Circular Arc |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
A circular loop is kept in that vertical plane which contains the north- south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop.
View SolutionDue to `10` ampere of current flowing in a circular coil of `10 cm` radius, the magnetic field produced at its centre is `3.14xx10^(-3) Weber//m^(3)`. The number of turns in the coil will be
View SolutionMagnetic field due to `0.1 A` current flowing through a circular coil of radius `0.1`m and `1000` turns at the centre of the coil is
View SolutionMagnetic field at the centre of coil of `n` turns, bent in the form of a square of side `2l`, carrying current `i`, is
View SolutionMagnetic field intensity at the centre of coil of `50` turns, radius `0.5m` and carrying a current of `2A` is
View SolutionOn meter length of wires carriers a constant current. The wire is bent to from a circular loop. The magnetic field at the centre of this loop is `B`. The same is now bent to form a circular loop of smaller radius to have four turns in the loop. The magnetic field at the centre of this loop `B`. The same is now bent to form a circular loop of smaller radius of have four turns in the loop. The magnetic field at the centre of this new loop is
View SolutionAn arc of a circle of radius `R` subtends an angle `(pi)/2` at the centre. It carriers a current `i`. The magnetic field at the centre will be
View SolutionAt a distance of `10 cm` from a long straight wire carrying current, the magnetic field is `0.04 T`. At the distance of `40 cm`, the magnetic field will be
View SolutionThe earth's magnetic induction at a certain point is `7xx10^(-5) Wb/m^(2)`. This is to be annulled by the magnetic induction at the centre of a circular conducting loop of radius `5 cm`. The required current in the loop is
View SolutionThe earth's magnetic field at a given point is `0.5xx10^(-5) Wb-m^(-2)`. This field is to be annulled by magnetic indcution at the centre of a circular conducting loop of radius `5.0 cm`. The current required to be flown in the loop is nearly
View SolutionA long wire carries a steady current . It is bent into a circle of one turn and the magnetic field at the centre of the coil is `B`. It is then bent into a circular loop of `n` turns. The magnetic field at the centre of the coil will be
View SolutionThe magnetic field due to a current carrying loop of radius ` 3 cm` at a point on the axis at a distance of `4 cm` from the centre is ` 54 muT`. What will be its value at the centre of loop ?
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius `a` and at distance `'a'` from centre of the coil and perpendicular to the axis of coil is
View SolutionTwo concentric coplanar circular loops of radii `r_(1)` and `r_(2)` carry currents of respectively `i_(1)` and `i_(2)` in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to `i_(1)` alone at the centre. if `r_(2)=2r_(1)`. the value of `i_(2)//i_(1)` is
View SolutionMagnetic fields at two points on the axis of a circular coil at a distance of `0.05m` and `0.2 m` from the centre are in the ratio `8:1`. The radius of the coil is
View SolutionTwo concentric circular coils of ten turns each are situated in the same plane. Their radii are `20` and `40 cm` and they carry respectively `0.2` and `0.3` ampere current in opposite direction. The magnetic field in `Wb//m^(3)` at the centre is
View SolutionA battery is connected between two points `A and B` on the circumference of a uniform conducting ring of radius `r` and resistance `R` . One of the arcs `AB` of the ring subtends an angle `theta` at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View SolutionA straight wire of length `(pi^(2))` meter is carrying a current of `2A` and the magnetic field due to it is measured at a point distant `1 cm` from it. If the wire is to be bent into a circles and is to carry the same current as before, the ratio of the magnetic field at its centre to that obtained in the first case would be
View SolutionTwo wires of same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionTwo concentric coils each of radius equal to `2 pi cm` are placed at right angles to each other ` 3 ampere and 4 ampere` are the currents flowing in each coil respectively. The magnetic induction in `weber//m^(2)` at the centre of the coils will be
`( mu_(0) = 4 pi xx 10^(-7) Wb// A.m)`
View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

View SolutionIf a long horizontal conductor is bent as shown in figure and a current I is passed in it, find the magnitude and direction of magnetic field induction at the centre of circular part.
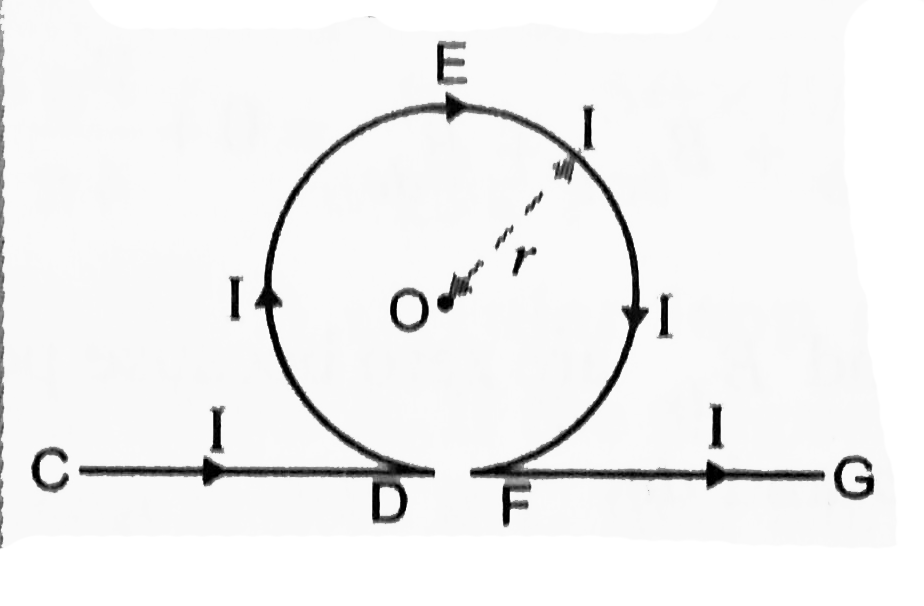
View SolutionA current `i` ampere flows in a circular arc of wire whose radius is `R`, which subtend an angle `3pi//2` radian at its centre. The magnetic induction `B` at the centre is

View SolutionThe magnetic induction at the centre `O` in the figure shown in
View SolutionIn the figure shown, the magnetic induction at the centre of the arc due to the current in portion `AB` will be

View SolutionThe magnetic induction at centre O Fig.
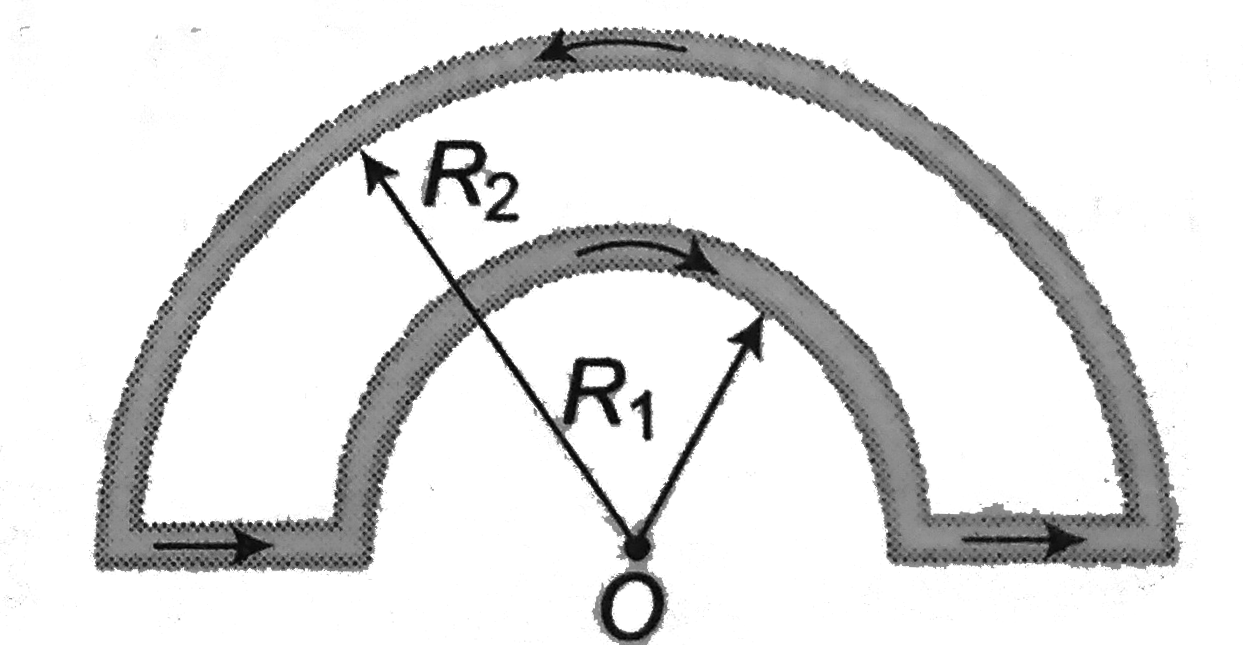
View SolutionIn the figure shown there are two semicircles of radii `r_(1)` and `r_(2)` in which a current `i` is flowing. The magnetic induction at the centre `O` will be

View SolutionThe magnetic field at centre O of the arc in Fig.
View Solution`A` and `B` are two concentric circular conductors of centre `O` and carrying currents `i_(1)` and `i_(2)` as shown in the adjacent figure. If ratio of their radii is `1:2` and ratio of the flux densities at `O` due to `A` and `B` is `1:3`, then the value of `i_(1)//i_(2)` is

View SolutionA wire carrying current `i` is shaped as shown. Section `AB` is a quarter circle of radius `r`. The magnetic field is directed
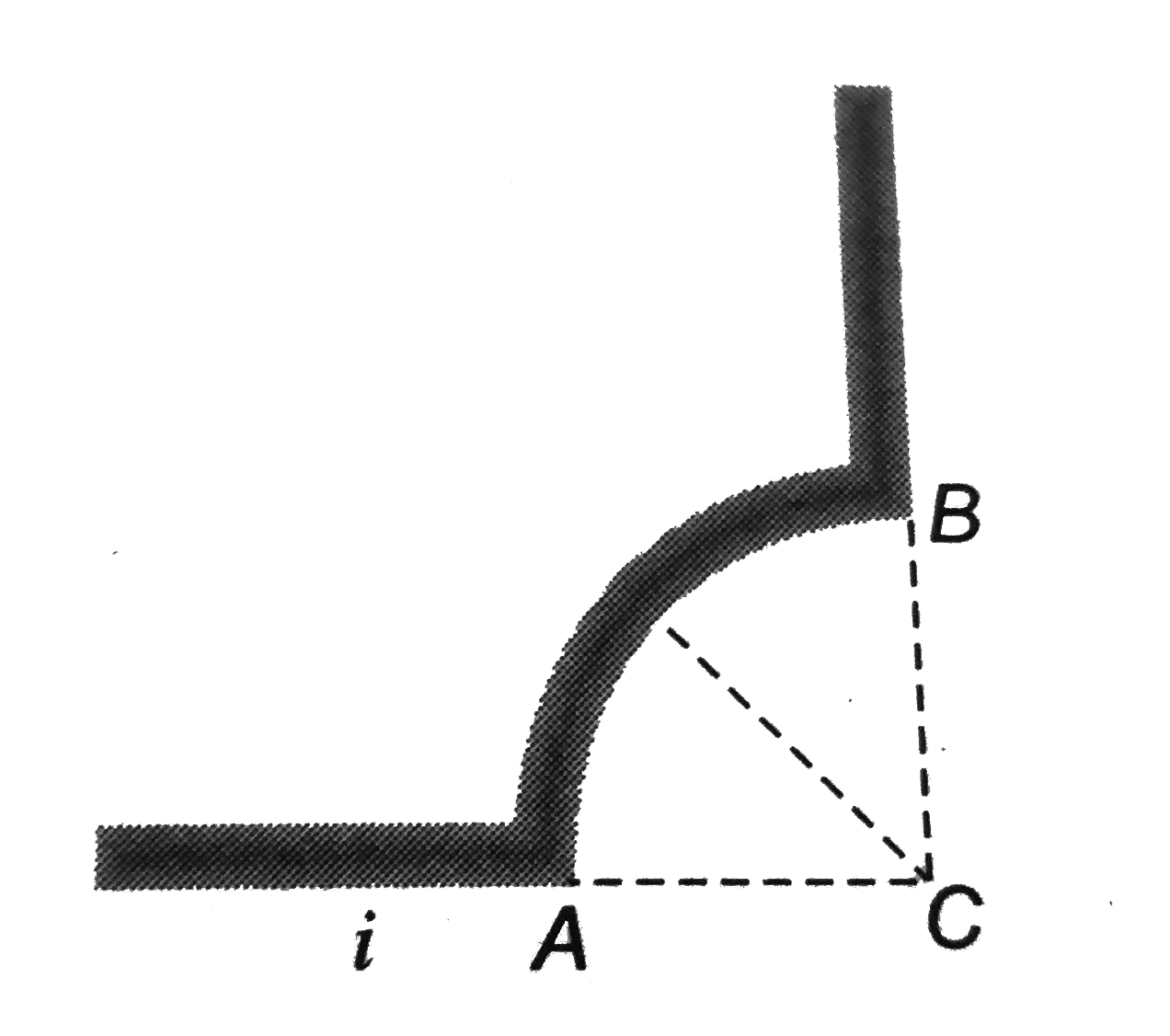
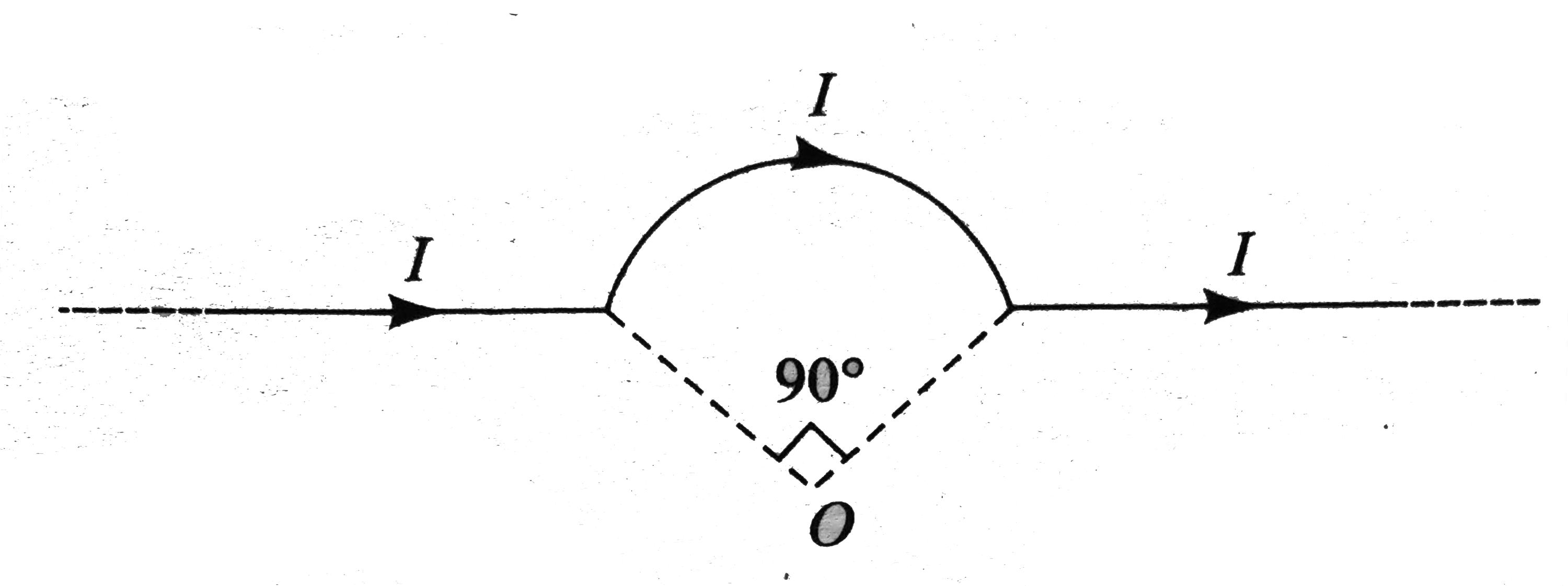
View SolutionA part of a long wire carrying a current `i` is bent into a circle of radius `r` as shown in figure. The net magnetic field at the centre `O` of the circular loop is
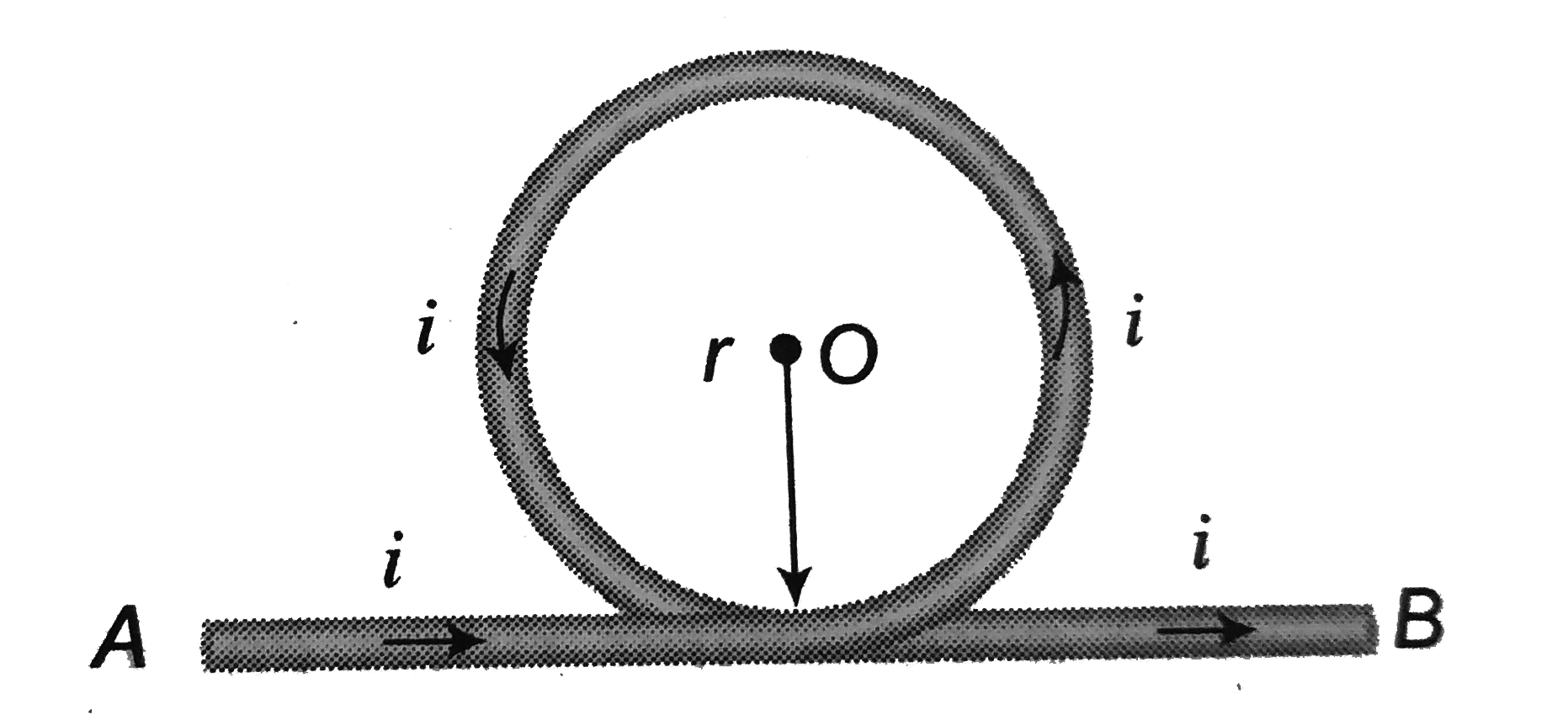
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionIn the figure, what is the magnetic field at the point `O`?

View SolutionThe resistances of three parts of a circular loop are as shown in Fig. The magnetic field at the centre O is (current enters at A and leaves at B and C as shown)
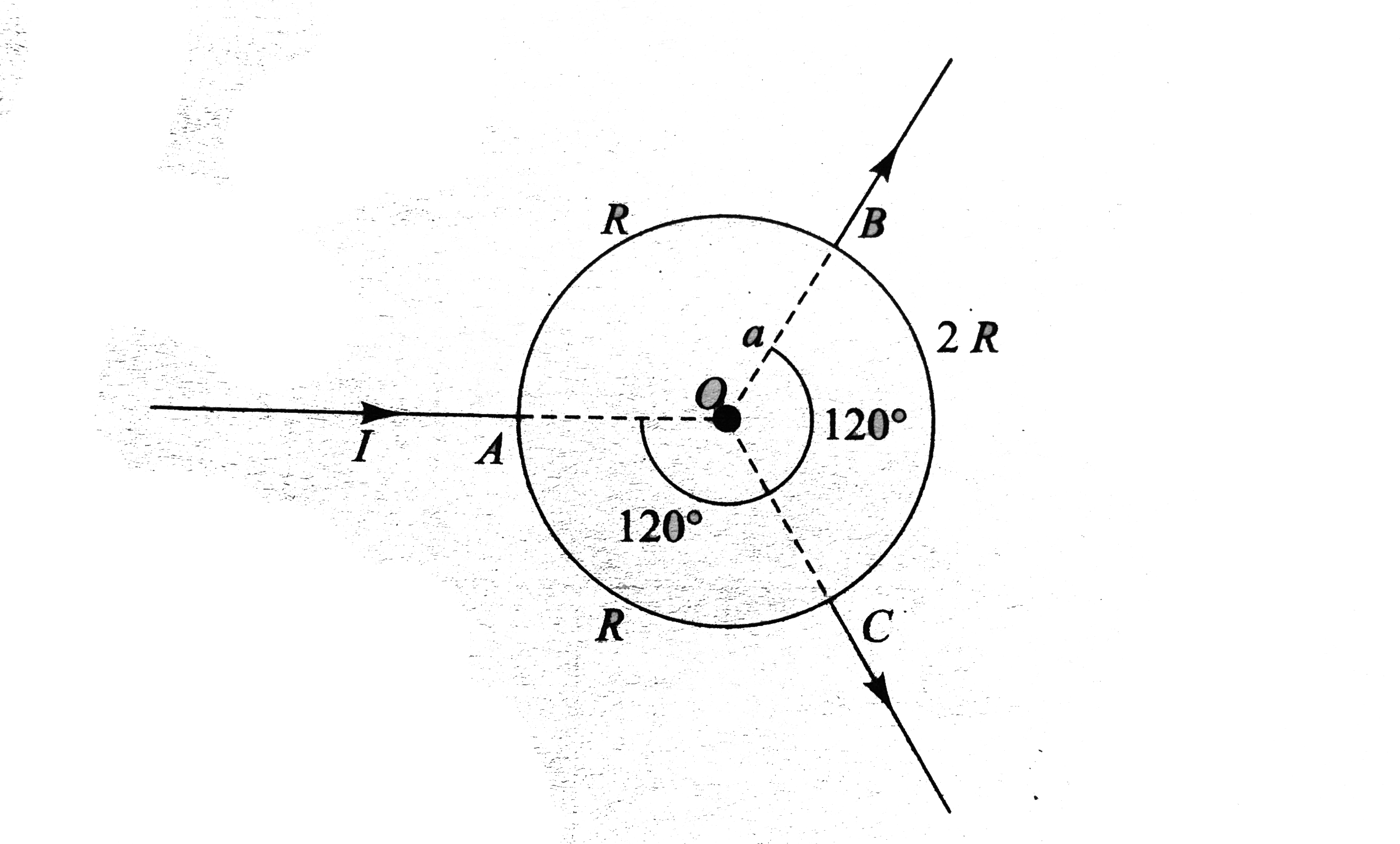
View SolutionConsidering magnetic field along the axis of a circular loop of radius `R`, at what distance from the centre of the loop is the field one eighth of its value at the centre ?
View SolutionIn Fig. infinite conducting rings each having current i in the direction shown are placed concentrically in the same plane as shown in the figure. The radii of rings are `r,2r,2^2r,2^3r,......,(oo)`. The magnetic field at the center of rings will be

View SolutionThe field normal to the plane of a wire of `n` turns and radius `r` which carriers `i` is measured on the axis of the coil at a small distance `h` from the centre of the coil. This is smaller than the field at the centre by the fraction.
View SolutionTwo identical wires `A and B` , each of length 'l', carry the same current `I`. Wire A is bent into a circle of radius `R and wire B` is bent to form a square of side 'a' . If ` B_(A) and B_(B)` are the values of magnetic field at the centres of the circle and square respectively , then the ratio `(B_(A))/(B_(B))` is :
View SolutionTwo circular coils X and Y, having equal number of turns and carrying currents in the same sense, subtend same solid angle at point O. If the smaller coil X is midway between O and Y and if we represent the magnetic induction due to bigger coil Y at O as `B_Y` and the due to smaller coil X at O as `B_X`, then find the ratio `B_X//B_Y`.

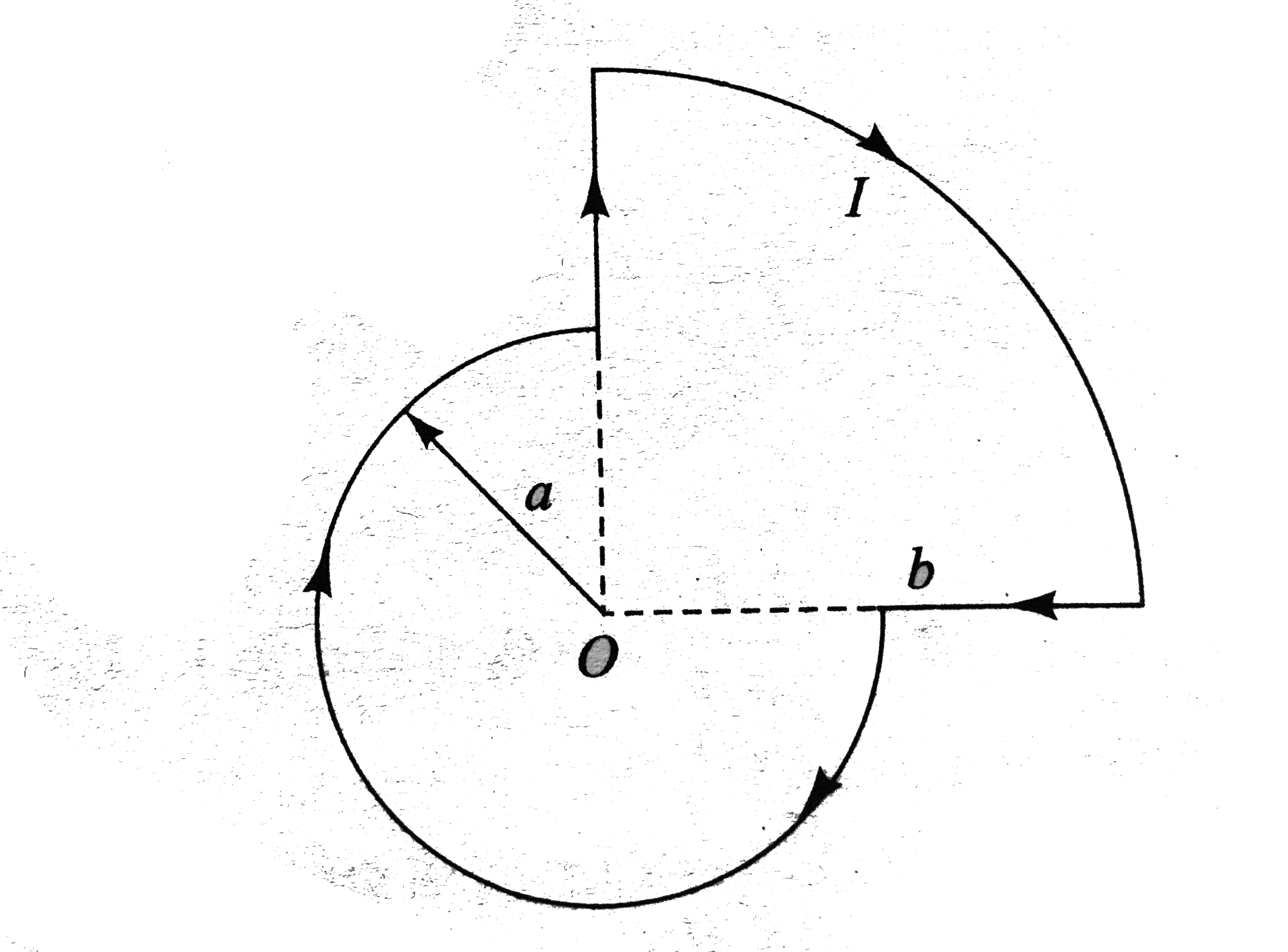
View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
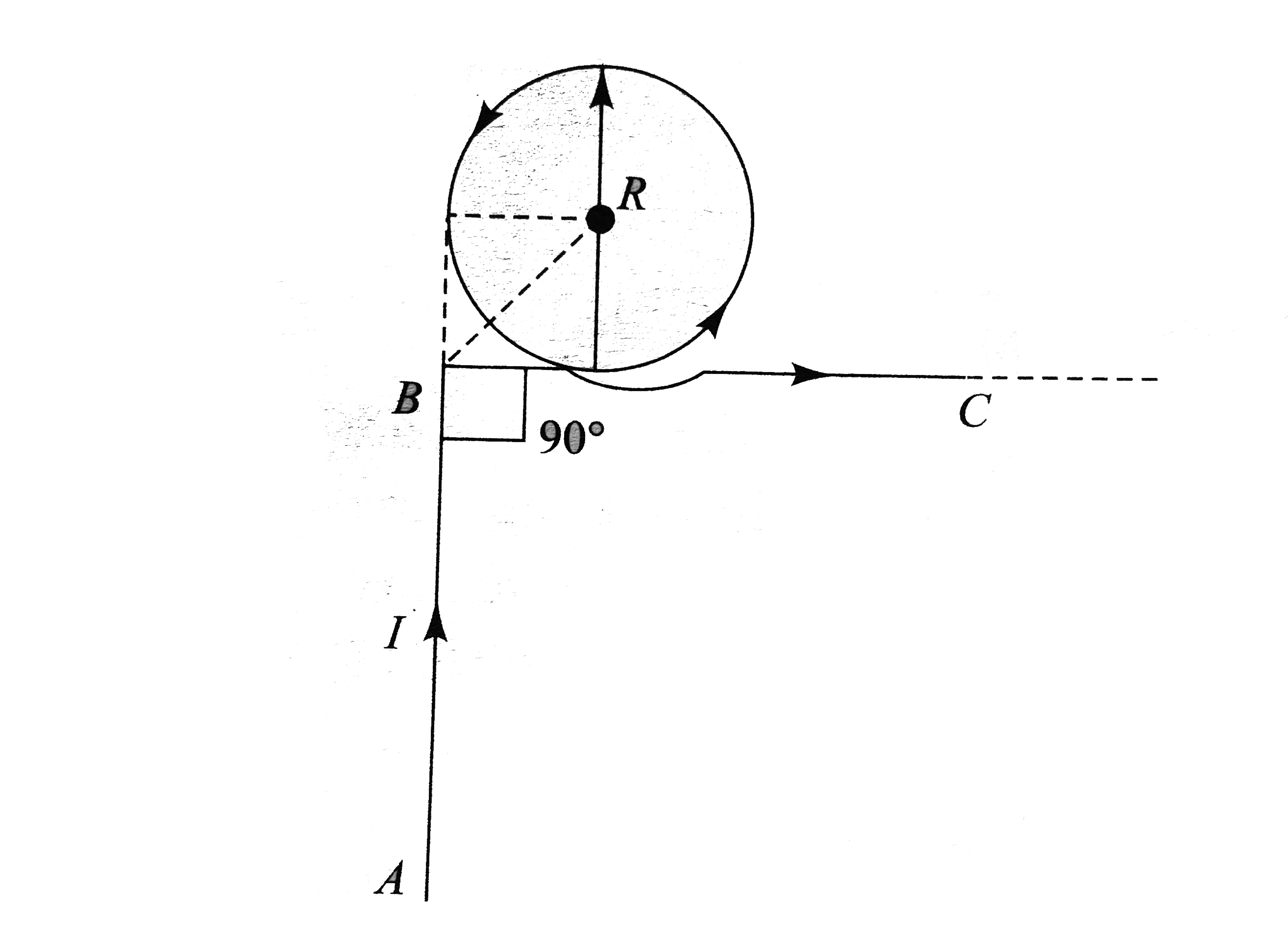
View SolutionFigure shows three cases: in all case the circular part has radius r and straight ones are infinitely long. For the same current the ratio of field B at centre P in the three case `B_1:B_2:B_3` is
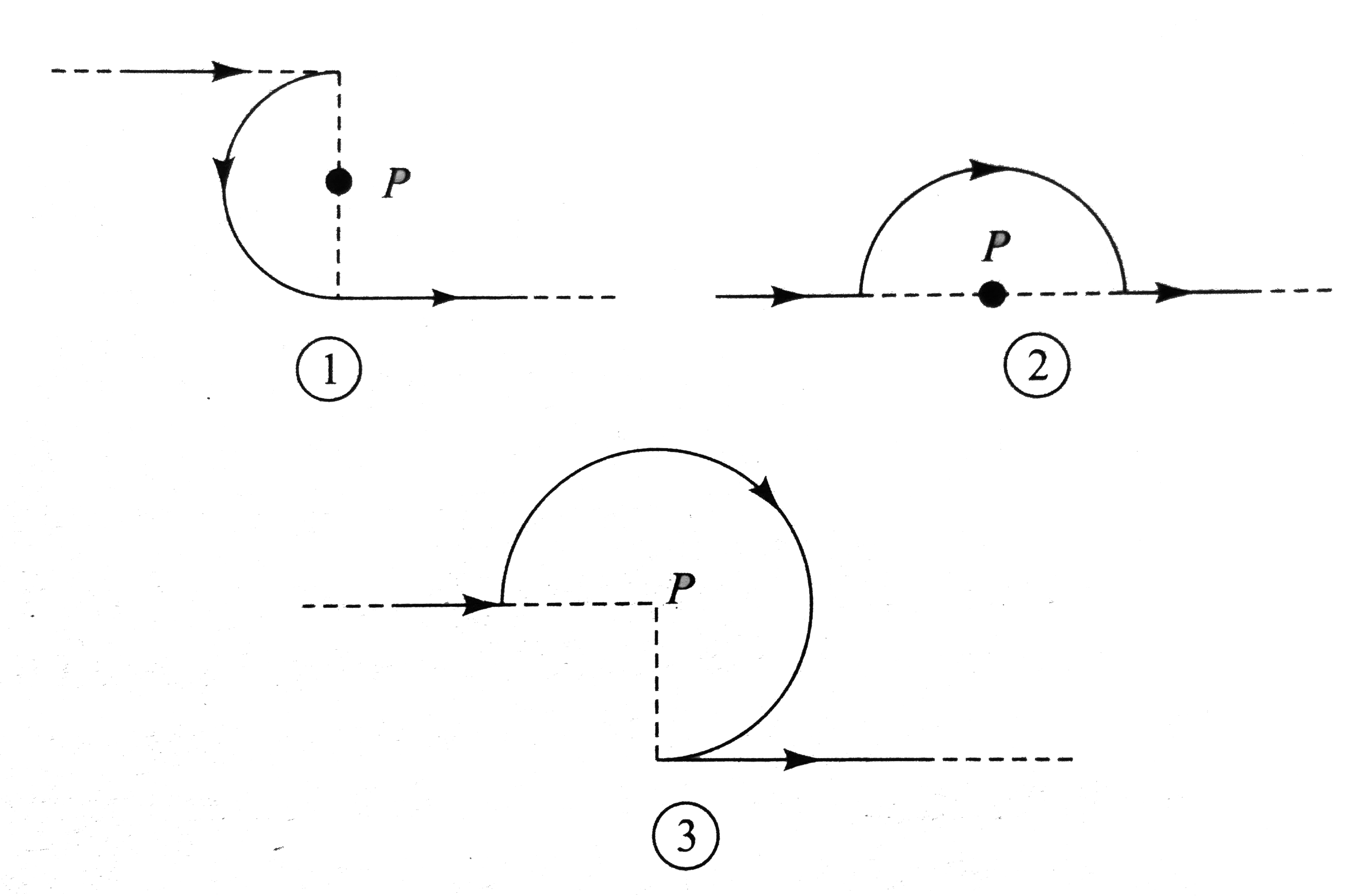
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a square coil made from the same length of wire will be
View SolutionA long straight non-conducting string carriers a charge density of `40 muC//m`. It is pulled along its length at a speed of `300 m//sec`. What is the magnetic field at a normal distance of `5 mm` from the moving string?
View SolutionIn a bent wire shown in figure, a current `I` is passed. Find the value of `B` at the common centre.
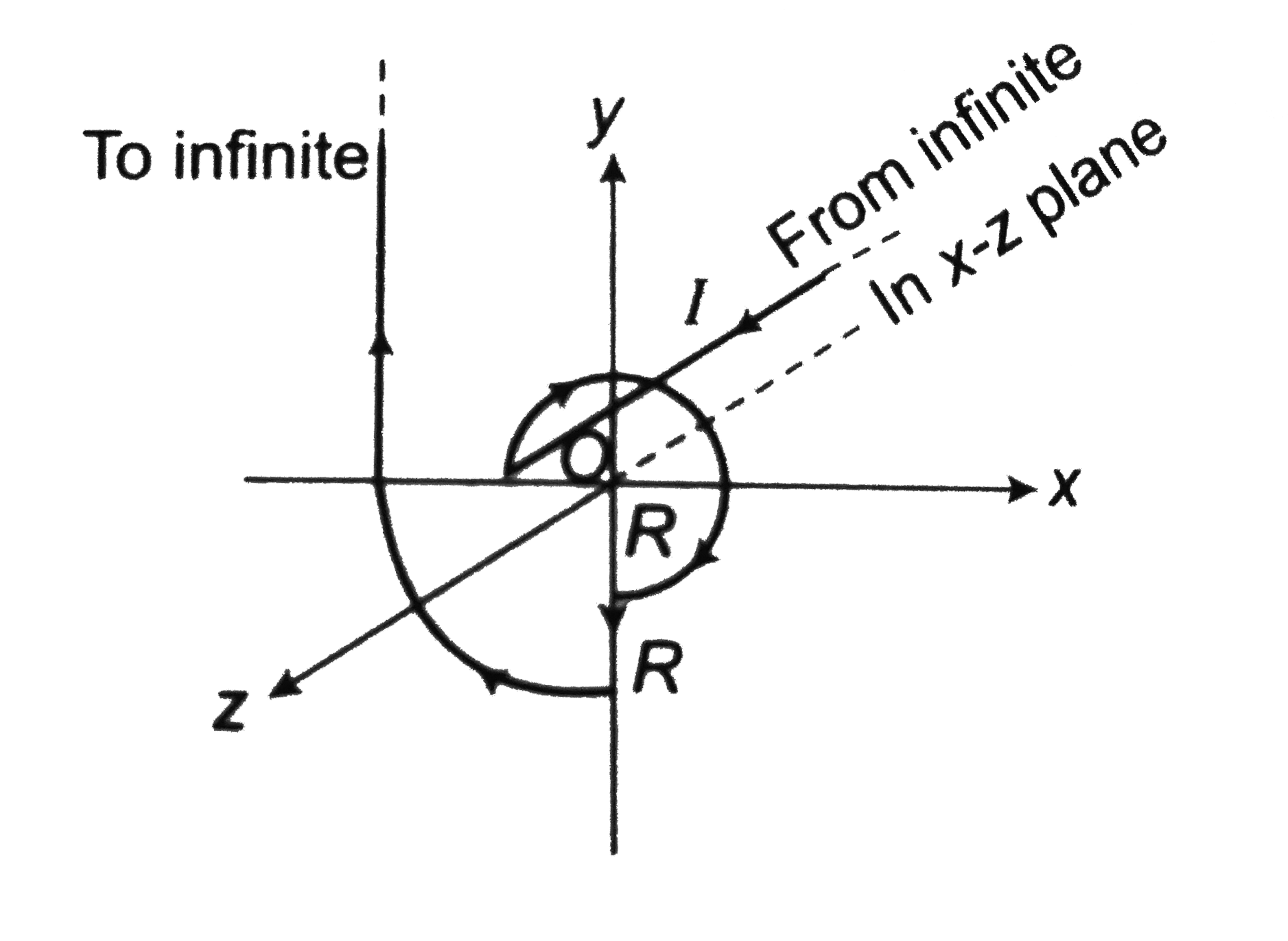
View SolutionThe current in the wire is `I`. The current comes from infinite parallel to `z`-axis and finally goes to finite paralle to `y`-axis as shown in the figure. Find magnetic field `O` in vector from for the following current configurations.
View SolutionA circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be `(1//8)^(th)` of its value at the centre of the coil is,
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA current `i` ampere flows in a circular arc of wire whose radius is `R`, which subtend an angle `3pi//2` radian at its centre. The magnetic induction `B` at the centre is

View SolutionAn otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
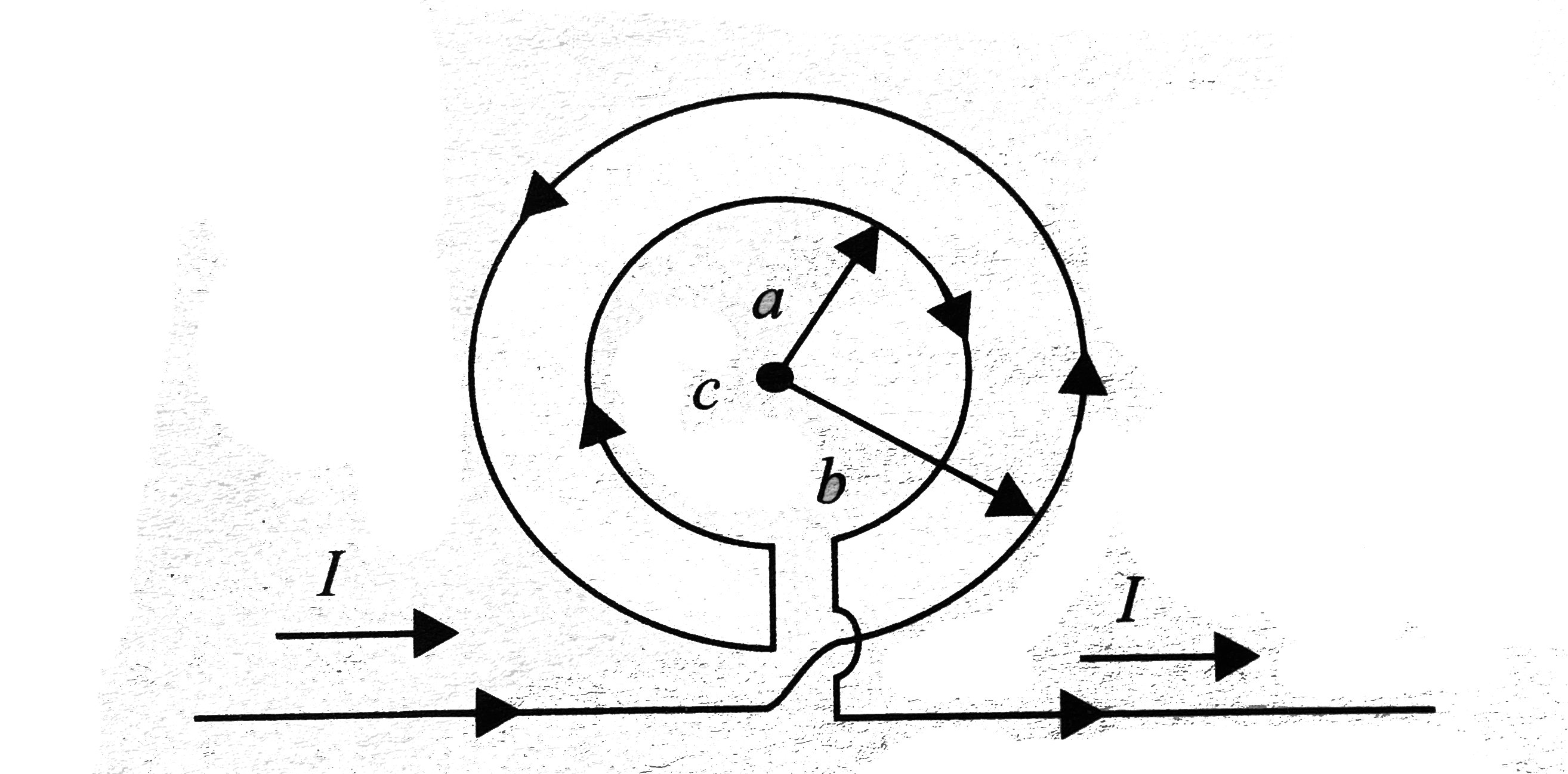
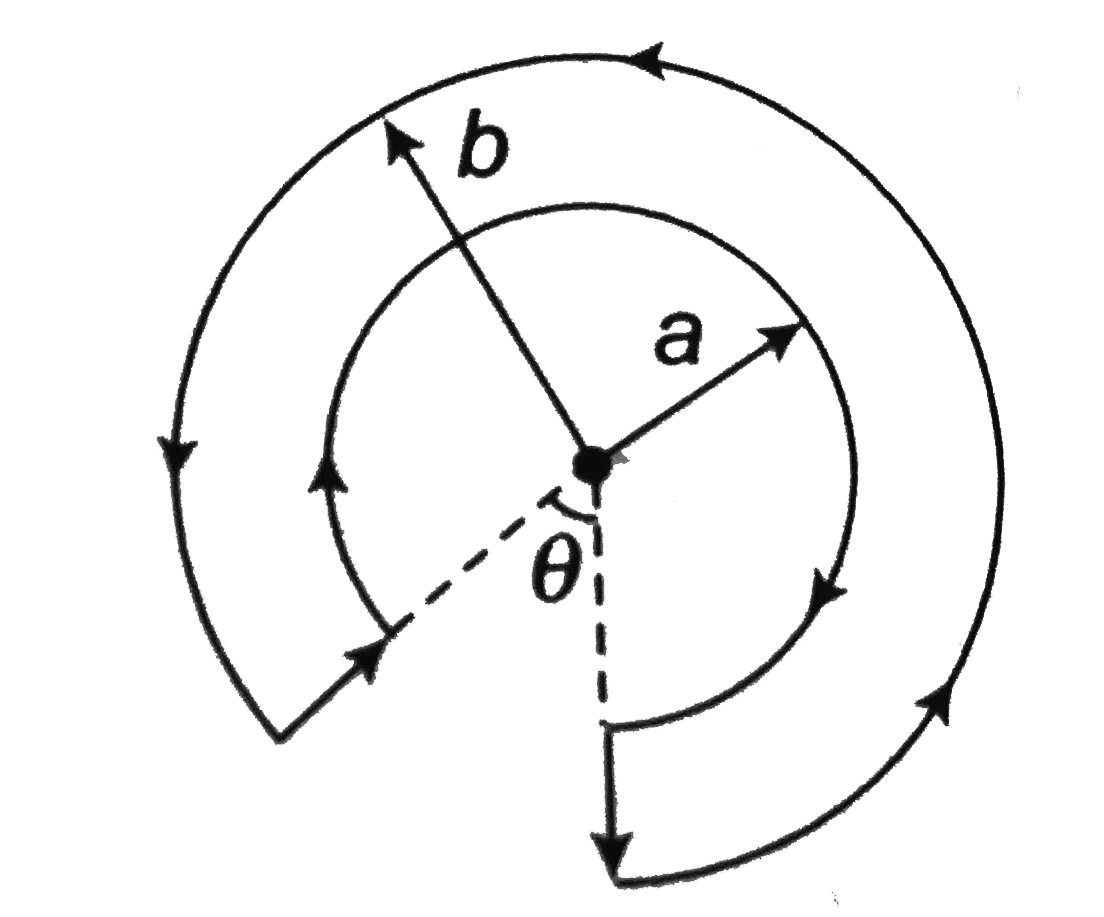
View SolutionFor `c=2a` if, the magnetic field at point P will be zero when

View SolutionA non - popular loop of conducting wire carrying a current `I` is placed as shown in the figure . Each of the straight sections of the loop is of the length ` 2a`. The magnetic field due to this loop at the point `P(a, 0 ,a)` points in the direction
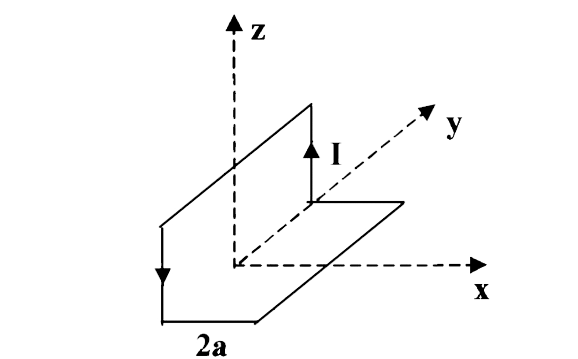
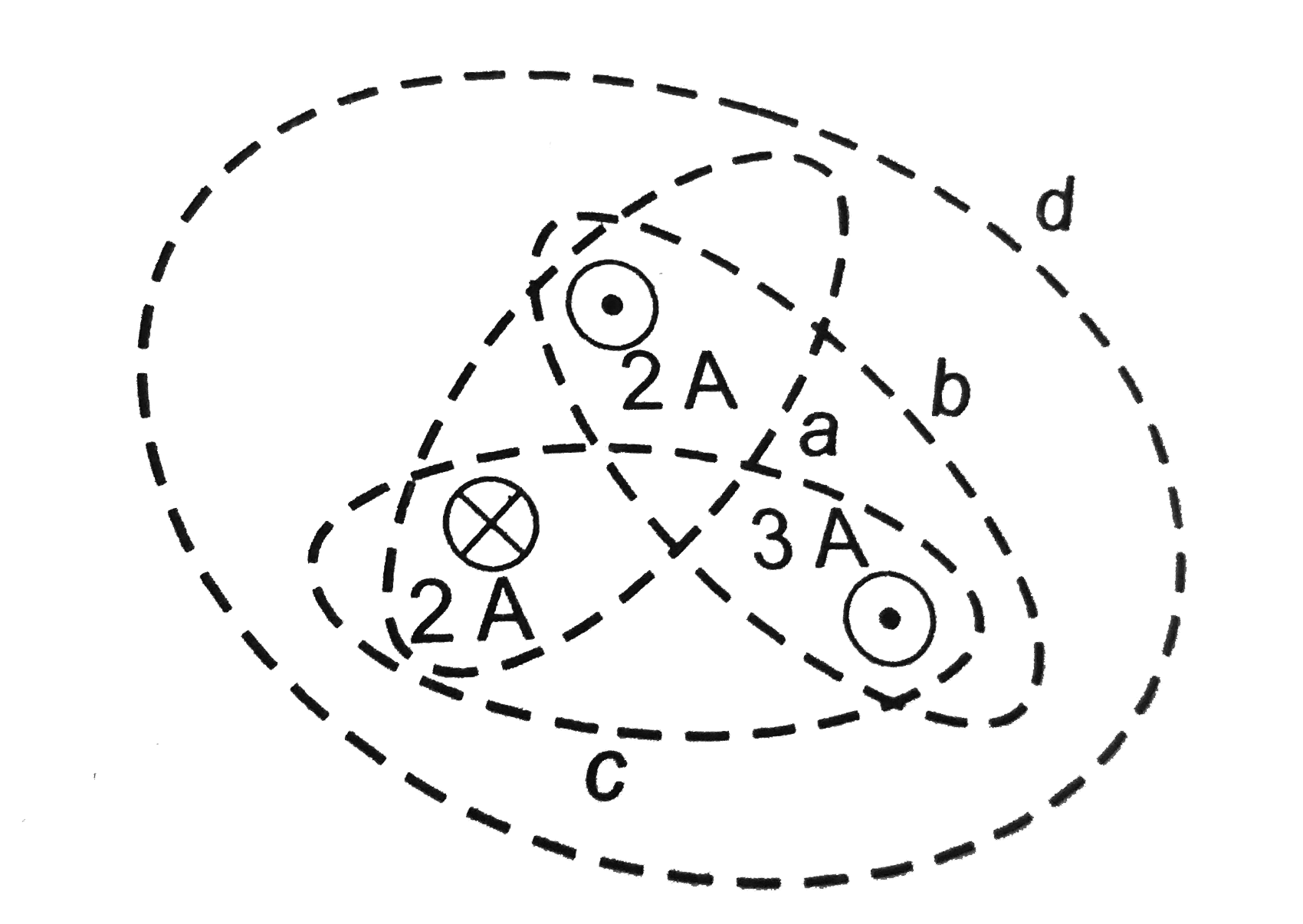
View SolutionRank the value of `ointvec(B)vec(dl)` for the closed paths shown in figure from the smallest to largest.
View SolutionA current ` I` flows along the length of an infinitely long, straight , thin - walled pipe. Then
View SolutionA current of `1//(4pi)` ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
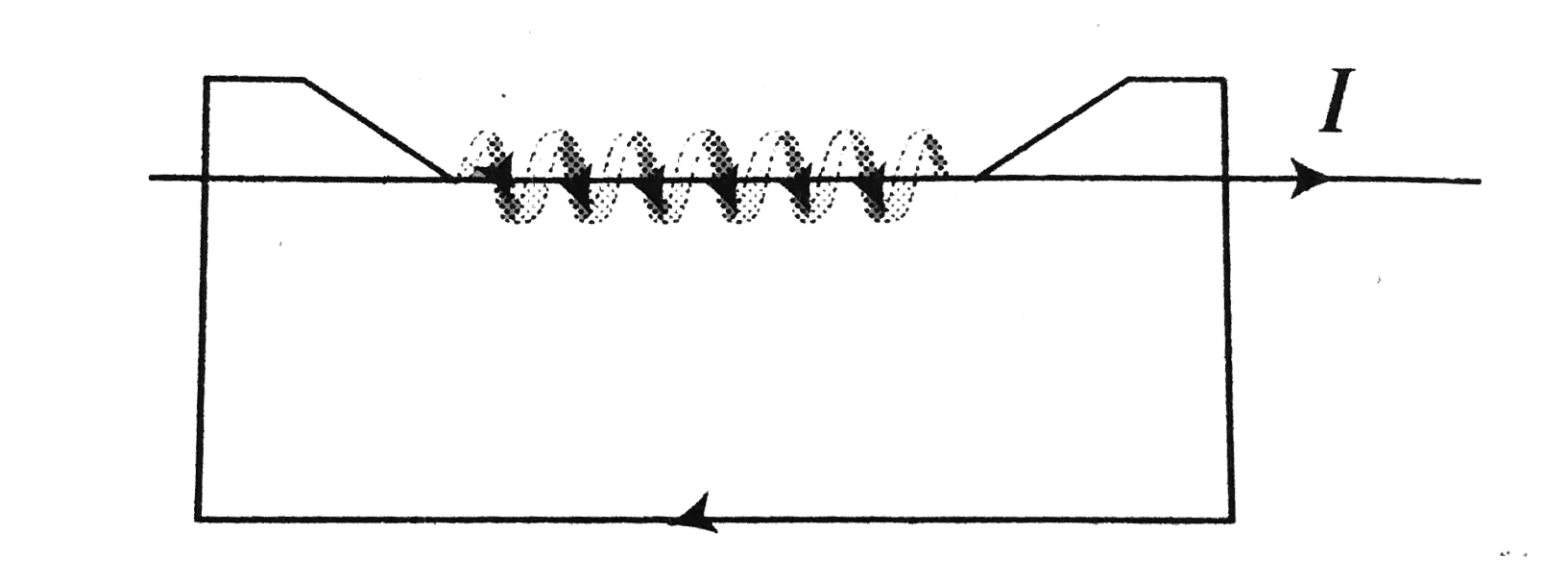
View SolutionIn the diagram shown, a wire carriers current `I`. The loop has `N` turns and part of helical loop on which arrows are drawn is outside the plane of paper. What is the value of the `oint vecB.vec(dl)` (as in Ampere's law) on the helical loop shown in the figure?
View SolutionA cylinder wire of radius R is carrying uniformly distributed current I over its cross-section. If a circular loop of radius r is taken as amperian loop, then the variation value of `oint vec(B)* vec(dl)` over this loop with radius 'r' of loop will be best represented by
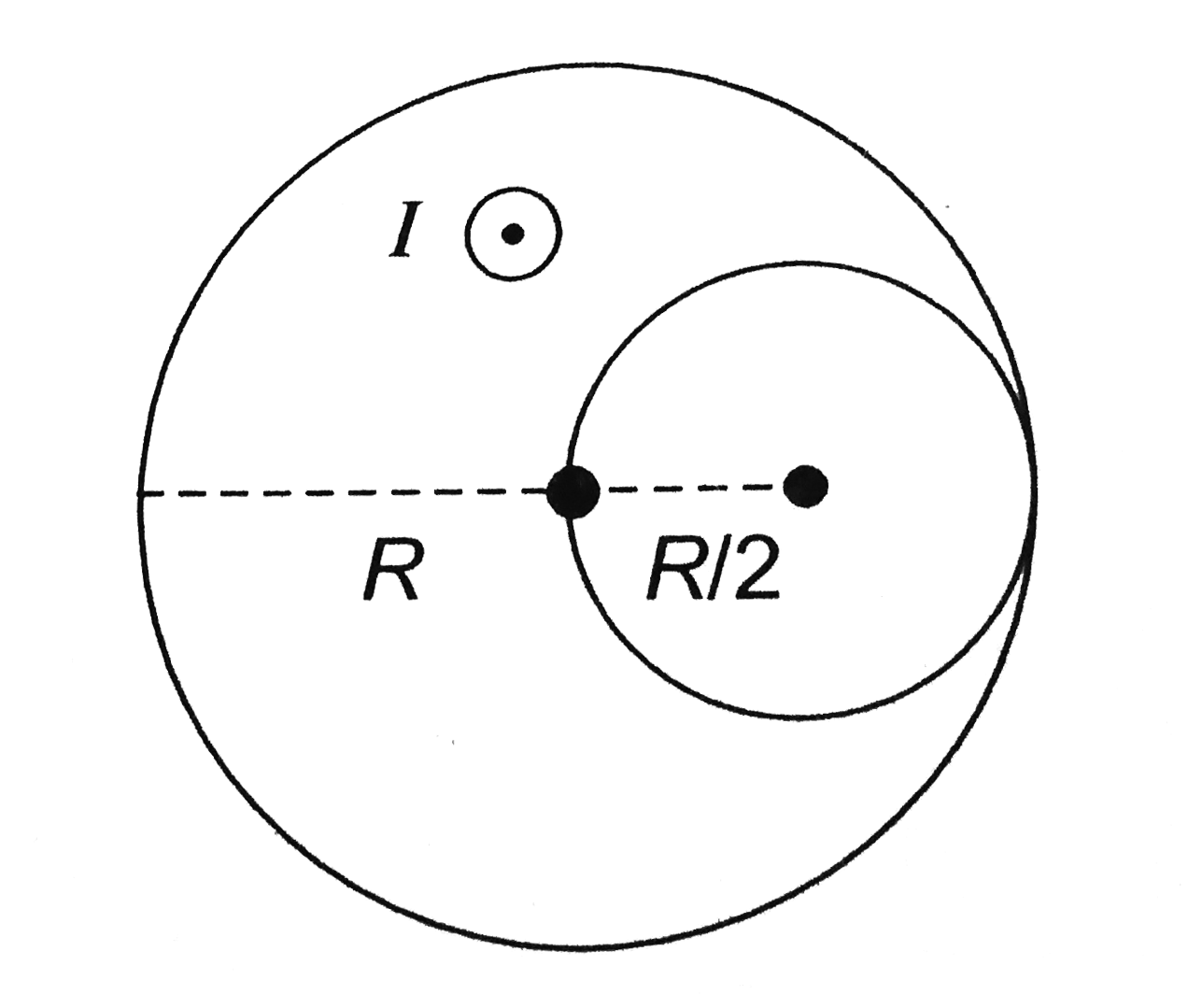
View SolutionCross-section of an infinite cylinder is shown. A current `I` uniformely distributed over its cross-section is flowing along its length. Now a cylinder of radius `R//2` is checked out of this. Then
View SolutionTwo identical wires `A and B` , each of length 'l', carry the same current `I`. Wire A is bent into a circle of radius `R and wire B` is bent to form a square of side 'a' . If ` B_(A) and B_(B)` are the values of magnetic field at the centres of the circle and square respectively , then the ratio `(B_(A))/(B_(B))` is :
View SolutionIf a long hollow copper pipe carriers a direct current, the magnetic field associated with the current will be:
View SolutionA current `i` ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance `r` meter from the axis is
View SolutionA long copper tube of inner radius `R` carriers a current `i`. The magnetic field `B` inside the tube is
View SolutionFive very long, straight insulated wires are closely bound together to form a small cable. Currents carried by the wires are: `I_1=20A, I_2=-6A, I_3=12A, I_4=-7A, I_5=18A`. (Negative currents are opposite in direction to the positive.) The magnetic field induction at a distance of 10cm from the cable is (current enters at A and leaves at B and C as shown)
View SolutionAxis of a solid cylinder of infinite length and radius R lies along y-axis. It carries a uniformly distributed current I along +y direction. Magnetic field at a point `(R//2, y, R//2)` is
View SolutionA coaxial cable consists of a thin inner conductor fixed along the axis of a hollow outer conductor. The two conductor carry equal currents in opposite directions. Let `B_1 and B_2` be the magnetic fields in the region between the conductors and outside the conductor, respectively. Then,
View SolutionA long, straight, hollow conductor (tube) carrying a current has two sections A and C of unequal cross sections joined by a conical section B. 1,2 and 3 are points on a line parallel to the axis of the conductor. The magnetic fields at 1,2 and 3 have magnitudes `B_1, B_2 and B_3`. Then,
View SolutionA long thin hollow metallic cylinder of radius `'R'` has a current `i` ampere. The magnetic induction `'B'` -away from the axis at a distance `r` from the axis varies as shown in
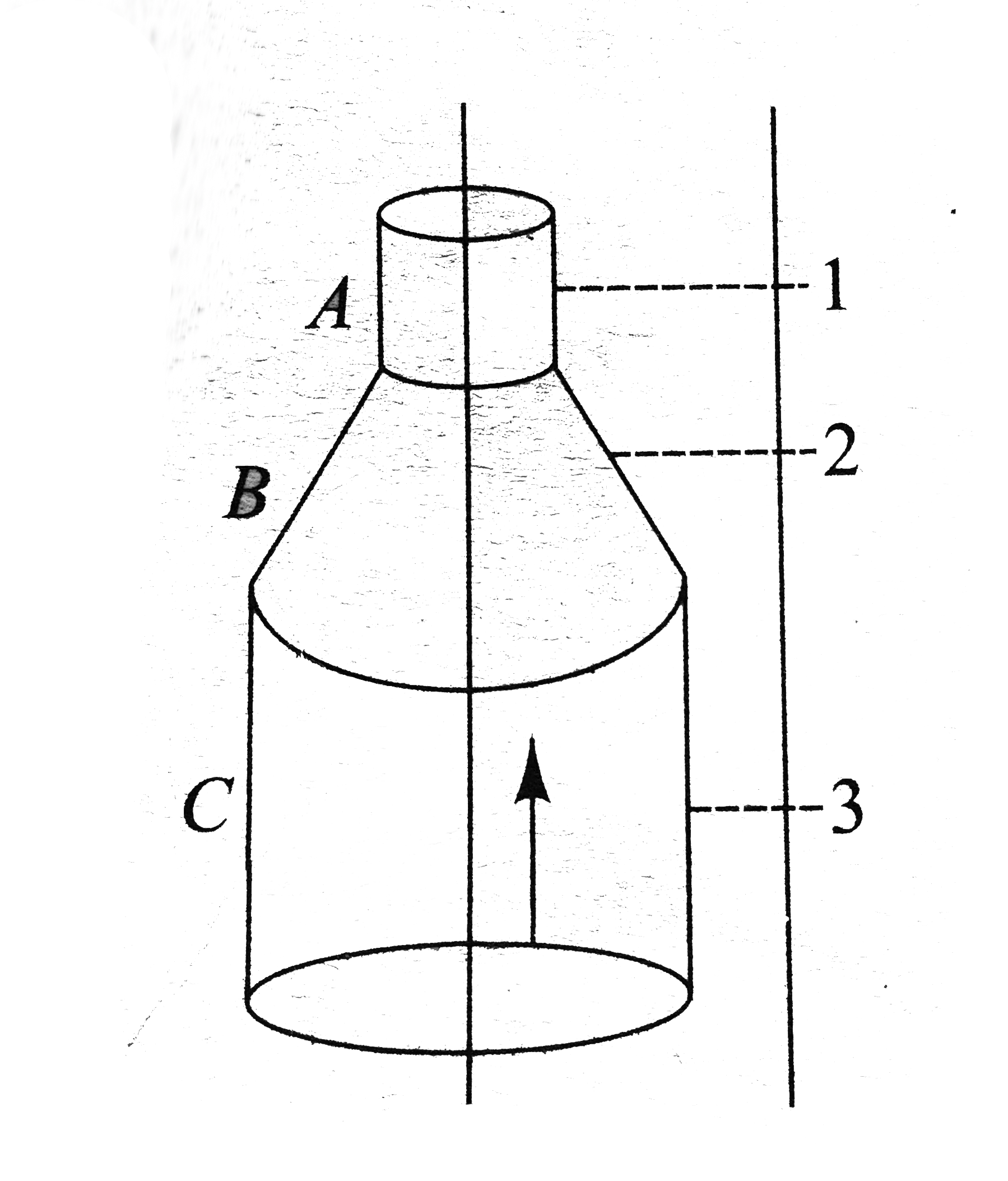
View SolutionFigure shows an Amperian path ABCDA. Part ABC is in vertical plane PSTU while part CDA is in horizontal plane PQRS. Direction of circulation along the path is shown by an arrow near point B and at D. `ointvecB.dvecl` for this path according to Ampere's law will be
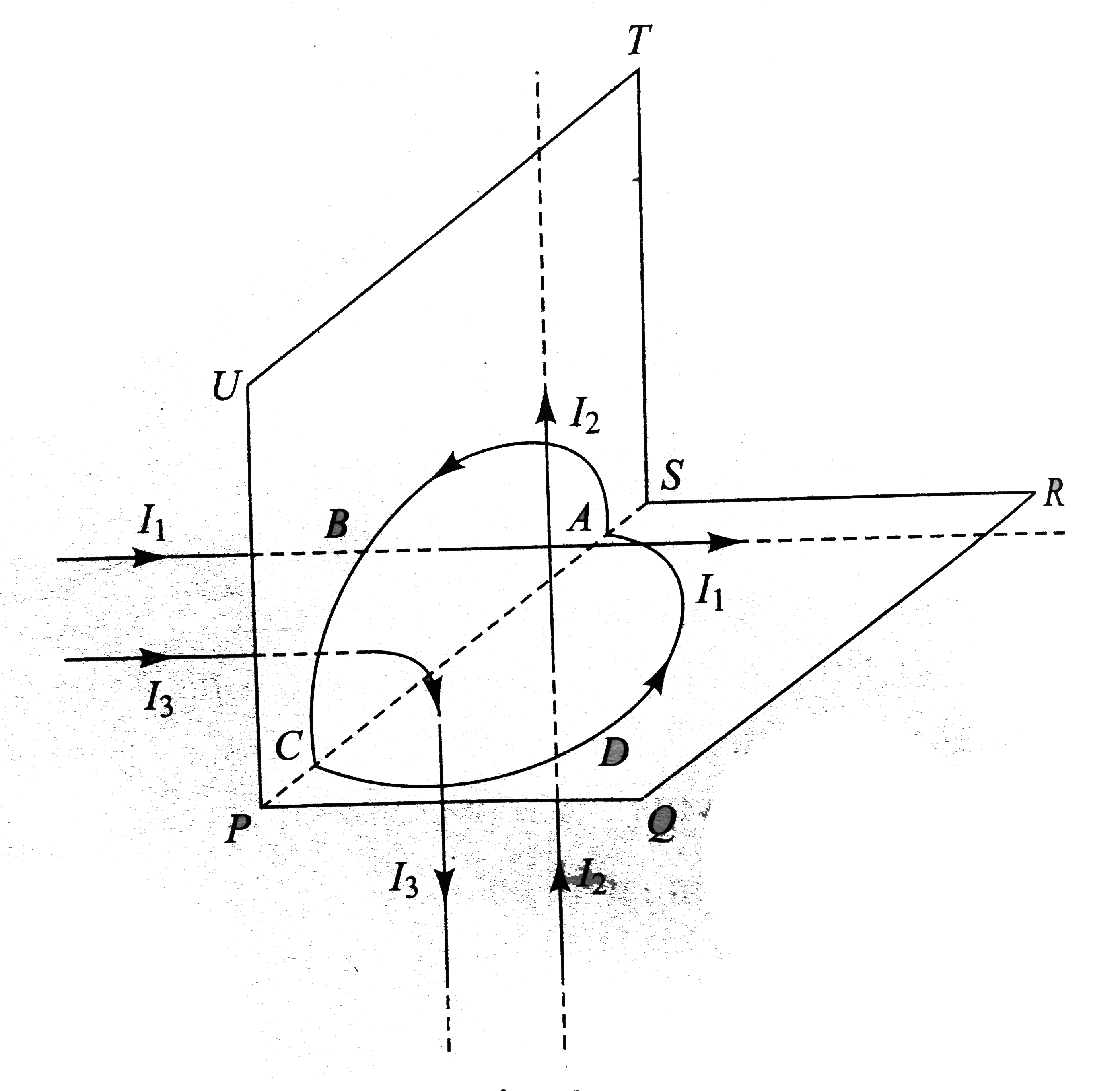
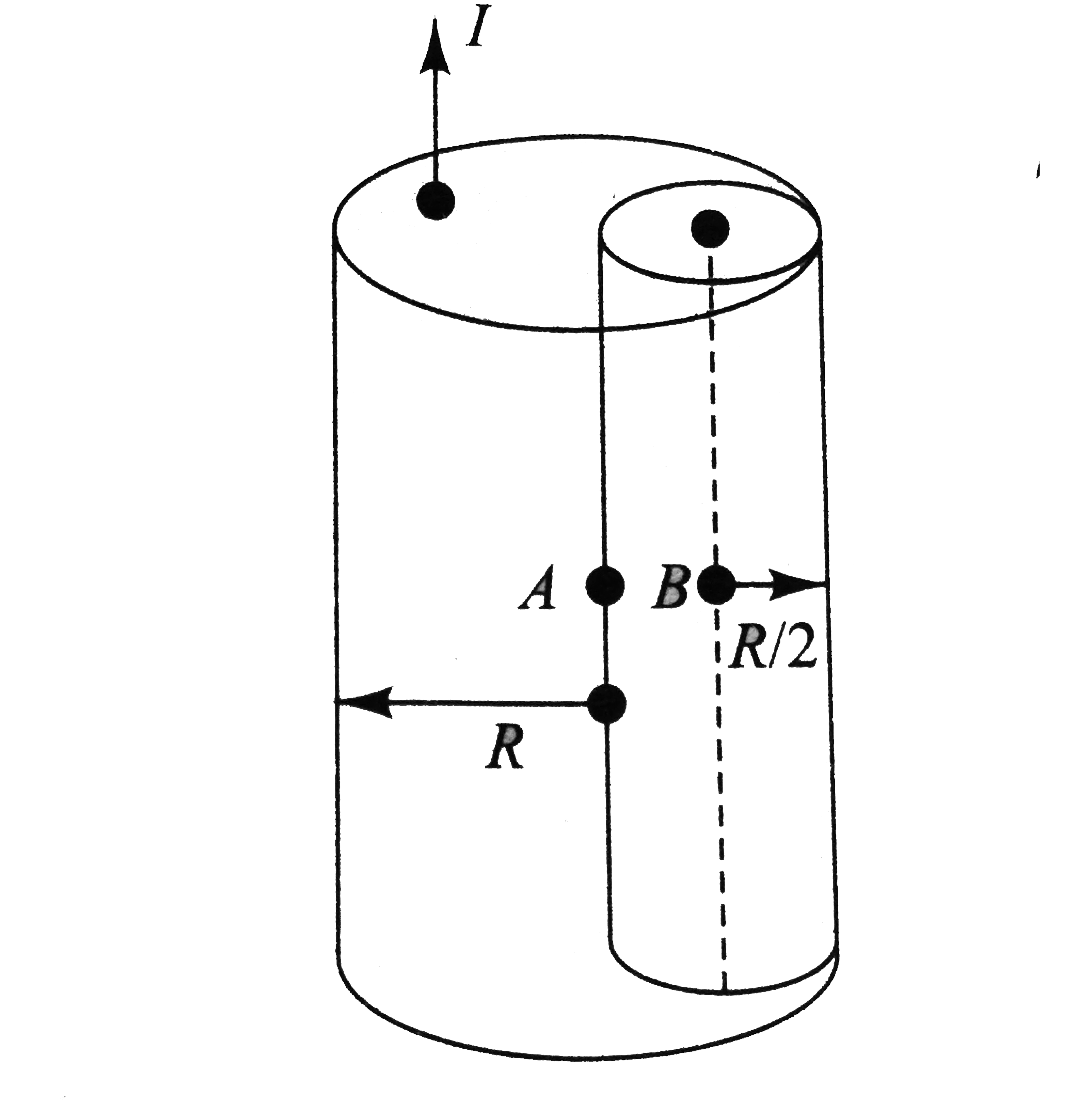
View SolutionFrom a cylinder of radius R, a cylider of radius `R//2` is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
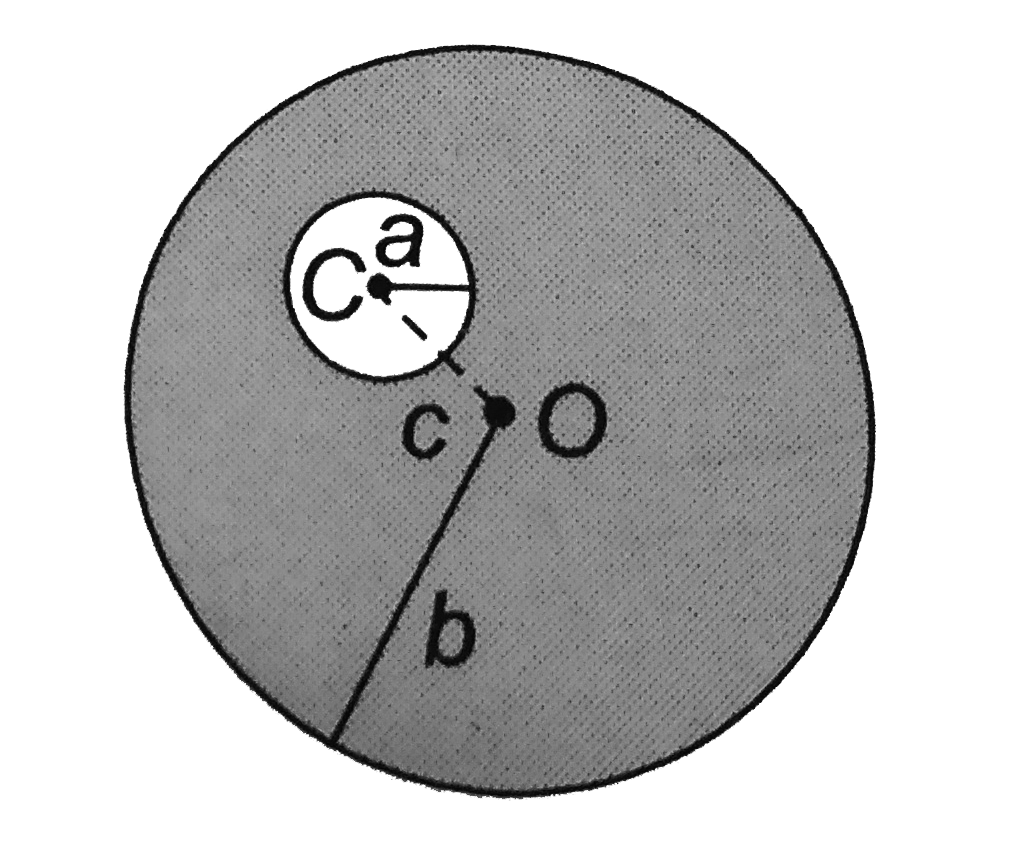
View SolutionA long straight metal rod has a very long hole of radius `'a'` drilled parallel to the rod axis as shown in the figure. If the rod carries a current `I`, find the magnetic field on axis of hole. Given `C` is the centre of the hole and `OC=c`.
View Solution
Magnetic Field Due To Circular Arc questions and complete solutions for chapter SOURCE AND EFFECT OF MAGNETIC FIELD of A2Z PHYSICS (HINGLISH) of Class 12
All Exercises from A2Z Class 12 PHYSICS SOURCE AND EFFECT OF MAGNETIC FIELD
- AIIMS Questions
- AIPMTNEET Questions
- Assertion- Reason
- Force On A Current Carrying Conductor In Magnetic Field
- Magnetic Dipole
- Magnetic Field Due To Circular Arc
- Magnetic Field Due To Current
- Motion Of Charged Particle In Magnetic Field
- Problems Based On Mixed Concepts
- Section B - Assertion Reasoning
- Section D - Chapter End Test