Complete Solutions to Exercise For Sesssion 1 of chapter PROPERTIES AND SOLUTION OF TRIANGLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES AND SOLUTION OF TRIANGLES |
| ARIHANT MATHS | Exercise For Sesssion 1 |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
In the given figure,if `AB= AC, angle BAD=30^(@)and AE=AD,` then x is equal to
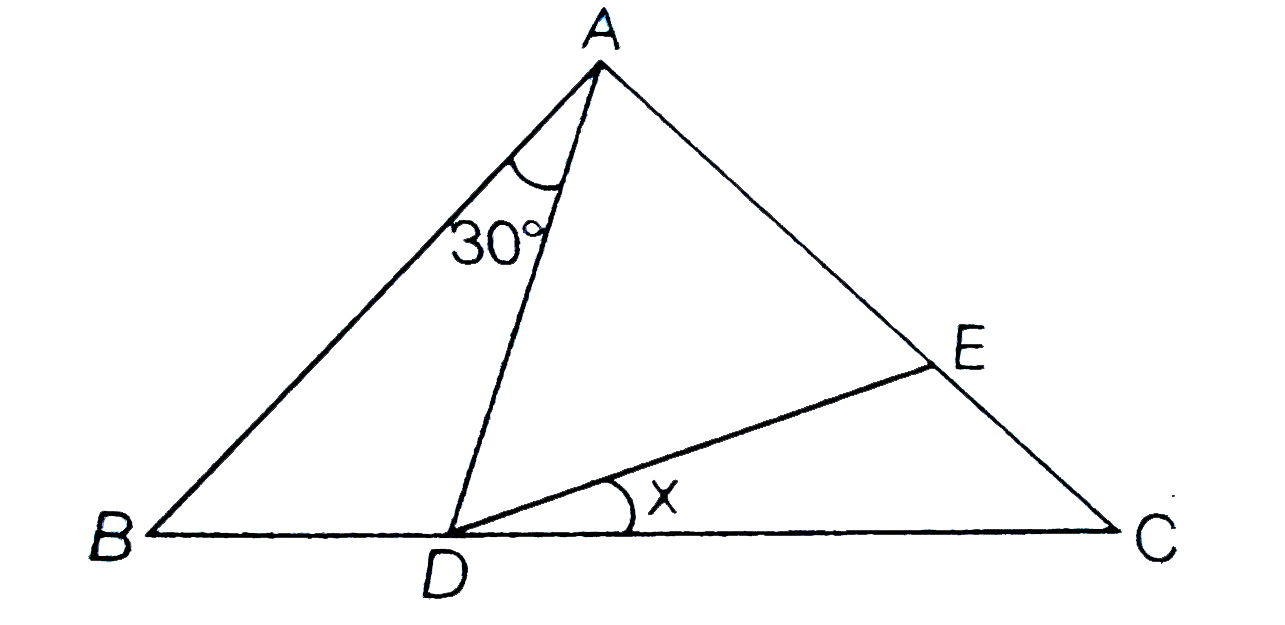
View SolutionIn `DeltaABC, a=4, b =12 and B=60^(@),` thn the vlaue of sin A is
View SolutionLet ABC be a triangle such that `angle A =45^(@) , angle B =75^(@),` then `a+c sqrt2` is equal to
View SolutionAngles A,B and C of a `DeltaABC` are in `AP. If b/c =(sqrt3)/(sqrt2),` then `angleA` is equal to
View SolutionIf `cot ""A/2 =(b+c)/(a),`then `DeltaABC` is
View SolutionIf in a `DeltaABC, (a^(2)-b^(2))/(a ^(2)+b^(2))=(sin (A-B))/(sin (A+B)),` then the triangle is
View SolutionIn any triangle `A B C ,` prove that: `(a^2sin(B-C))/(sinB+s in C)+(b^2sin(C-A))/(sinC+s in A)+(c^2sin(A-B))/(sinA+s in B)=0`
View SolutionIn any `DeltaABC,` is `2 cos B=a/c,` then the triangle is
View SolutionProve that `((a+b+c)(b+c-a)(c+a-b)(a+b-c))/(4b^2c^2)=sin^2A`
View SolutionIf a `cos A =b cos B, ` then the triangle is
View SolutionIn a `Delta ABC, (a+b+c) (b+c-a) = gamma bc` if
View SolutionIf : `a = 9, b = 8 and c = x` satisfies 3 cos C = 2, then : x =
View SolutionIn `DeltaABC, if sin^2 A+ sin^2 B = sin^2 C`, then the triangle is
View SolutionThe lengths of the sides of a triangle are `alpha-beta, alpha+beta` and `sqrt(3alpha^2+beta^2), (alpha>beta>0)`. Its largest angle is
View SolutionIn any triangle, `(1+ cos (A-B)cos C)/(1+cos (A-C)cos B)=`
View SolutionThe sides a, b, c of a triangle ABC are in arithmetic progression and 'a' is the smallest side. What is cos A equal to ?
View SolutionIn a `DeltaABC, a ^(2) cos 2B+b^(2) cos 2A+2ab cos (A-B)=`
View SolutionIn any `DeltaABC, 2 [bc cos A + ca cos B+ ab cos C]=`
View SolutionIn a `DeltaABC, tan ""1/2 (A+B) . Cot""1/2(A-B)` is equal to
View SolutionIf in a `Delta ABC, b =sqrt3, c=1 and B-C =90^(@), ` then `angle A` is
View Solution
Exercise For Sesssion 1 questions and complete solutions for chapter PROPERTIES AND SOLUTION OF TRIANGLES of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS PROPERTIES AND SOLUTION OF TRIANGLES
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Sesssion 1
- Exercise For Sesssion 2
- Exercise For Sesssion 3
- Exercise For Sesssion 4
- Exercise For Sesssion 5
- Exercise For Sesssion 6
- Exercise For Sesssion 7
- Exercise For Sesssion 8