Complete Solutions to EXERCISE # III of chapter FLUID MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUID MECHANICS |
| BANSAL | EXERCISE # III |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA `3.6m` long vertical pipe resonates with a source of frequency `212.5 Hz` when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height `H (~~ 3.6m)`. A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of `H`. If the radii of the pipe and the hole are `2 xx 10^(-2)m` and `1 xx 10^(-3)m` respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air `340m//s` and `g = 10m//s^(2)`.
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density `rho` where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
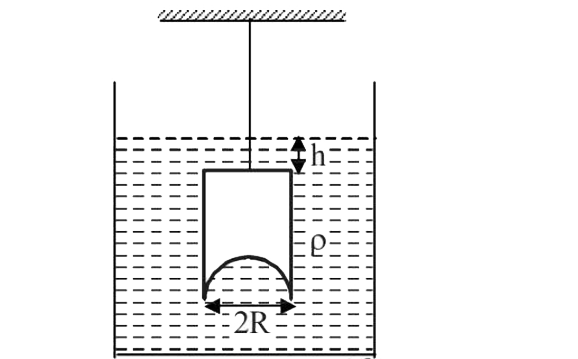
View SolutionA wooden block, with a coin placed on its top, floats in water as shown in figure. The distance l and h are shown here. After some time the coin falls into water. Then

View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.
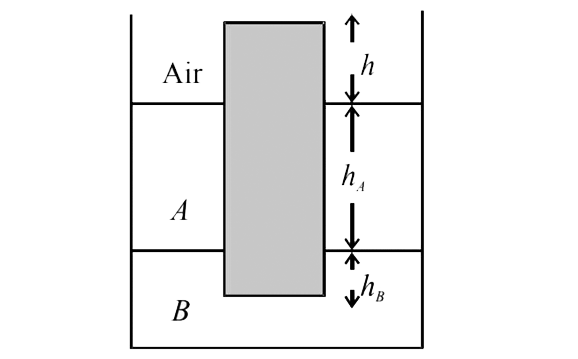
(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionConsider a horizontally oriented syringe containing water located of a height of `1.25 m` above the ground. The diameter of plunger is `8 mm` and the diameter if the nozzle is `2 mm`. The plunger is pushed with a constant speed of `0.25 m//s`. Find the horizontal range of water stream on the ground. Take `g = 10 m//s^2`.
 .
.
View SolutionA solid sphere of radius `R` is floating in a liquid of density `sigma` with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If `a//A=0.1` then `v^2` is (where v is the velocity of water coming out of the hole)
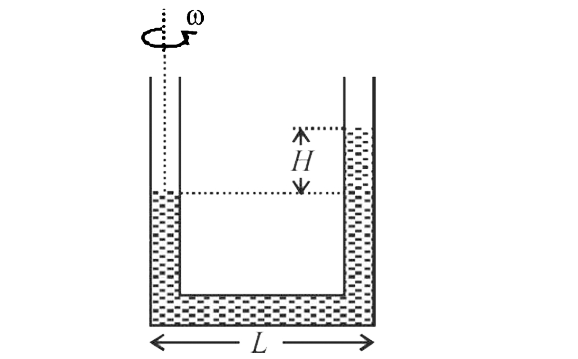
View SolutionA U tube is rotated about one of it's limbs with an angular velocity `omega`. Find the difference in height H of the liquid (density `rho`) level, where diameter of the tube `dlt lt L`.
View SolutionA wooden cylinder of diameter 4 r, height H and density `rho//3` is kept on a hole of diameter 2 r of a tank, filled with water of density `rho` as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height `h_(1)` above the cylinder, the block just start moving up. Then the value of `h_(1)` is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density `rho//3`.

Situation I: Initially, the tank is filled with water of density `rho` to a height such that the height of water above the top of the block is `h_1` (measured from the top of the block).
Situation II: The water is removed from the tank to a height `h_2` (measured from the bottom of the block), as shown in the figure. The height `h_2` is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level `h_2` (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionA wooden cylinder of diameter 4 r, height H and density `rho//3` is kept on a hole of diameter 2 r of a tank, filled with water of density `rho` as shown in the

If height `h_(2)` of water level is further decreased, then
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density `rho//3`.

Situation I: Initially, the tank is filled with water of density `rho` to a height such that the height of water above the top of the block is `h_1` (measured from the top of the block).
Situation II: The water is removed from the tank to a height `h_2` (measured from the bottom of the block), as shown in the figure. The height `h_2` is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level `h_2` (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionStatement-1 : The stream of water flowing at high speed from a garden hose pipe tends to spread like a foundtion when held vertically up, but tends to narrow down when held vertically down.
Statement-2 : In any steady flow of an incompressible fluid, the volume flow rate of the fluid remain constant.
View SolutionA glass tube of uniform internal radius `(r)` has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End `1` has a hemispherical soap bubble of radius `r`. End `2` has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure `=1.0xx10^5N//m^2`, density of water=1000kg//m^3` and `g=10m//s^2`. Neglect any effect of surface tension.]
View SolutionTwo soap bubbles `A` and `B` are kept in a closed chamber where the air is maintained at pressure `8 N//m^(2)`. The radii of bubbles `A` and `B` are `2 cm` and `4 cm`, respectively. Surface tension of the soap. Water used to make bubbles is `0.04 N//m`. Find the ratio `n_(B)//n_(A)`, where `n_(A)` and `n_(B)` are the number of moles of air in bubbles `A` and `B` respectively. [Neglect the effect of gravity.]
View SolutionA thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If `rho_c` is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is
View Solution
EXERCISE # III questions and complete solutions for chapter FLUID MECHANICS of BANSAL PHYSICS (HINGLISH) of Class 12