Complete Solutions to SOLVED EXAMPLES of chapter FLUID MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUID MECHANICS |
| BANSAL | SOLVED EXAMPLES |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
If pressure at half the depth of a lake is equal to 2//3 pressure at the bottom of the lake then what is the depth of the lake ?
View SolutionTwo bodies are in equilibrium when suspended in water from the arms of balance. The mass of one body is 36 g and its density is `9 g// cm^3` If the mass of the other is 46 g, its density in `g//cm^3` is
View SolutionAn inverted bell lying at the bottom of a lake `47.6 m` deep has `50 cm^3` of air trapped in it. The bell is brought to the surface of the lake. The volume of the trapped air will be (atmospheric pressure `= 70 cm` of `Hg` and density of `Hg = 13.6 g//cm^3`).
View SolutionA U -tube in which the cross - sectional area of the limb on the left is one quarter, the limb on the right contains mercury `(density 13.6 g//cm^3).` The level of mercury in the narrow limb is at a distance of 36 cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb if the left limb is filled to the top with water ?
View SolutionA uniformly tapering vessel is filled with a liquid of density `900 kg // m`. The force that acts on the base of the vessel due to the liquid is `(g = 10 ms^(-2))`

View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density `0.85 g//cm^3` The pressure at the bottom of the tank, due to these liquids is
View SolutionA siphon in use is demonstrated in the following in siphon is `1.5 gm//c c`. The pressure difference between the point `P` and `S` will be
View SolutionThe height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ration of density of mercury to that of air is `10^(4)`. The height of the hill is
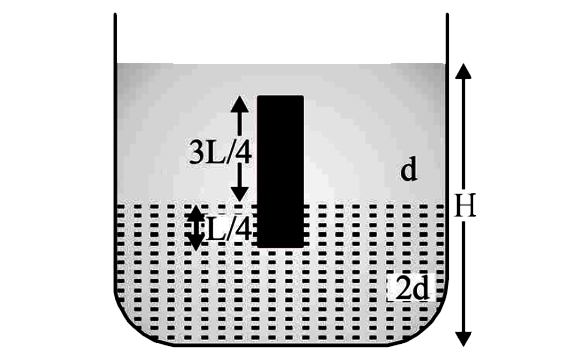
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure `P_0`. Then density D of solid is given by
View SolutionDensity of ice is `rho` and that of water is `sigma`. What will be the decrease in volume when a mass `M` of ice melts?
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
View SolutionTwo substances of densities `rho_(1)` and `rho_(2)` are mixed in equal volume and the relative density of mixture is `4`. When they are mixed in equal masses, the relative density of the mixture is 3. the values of `rho_(1)` and `rho_(2)` are:
View SolutionA body of density d is counterpoised by Mg of weights of density `d_1` in air of density d. Then the true mass of the body is
View SolutionA wooden block, with a coin placed on its top, floats in water as shown in figure. The distance l and h are shown here. After some time the coin falls into water. Then

View SolutionA hemispherical bowl just floats without sinking in a liquid of density `1.2xx10^(3)kg//m^(3)`. If outer diameter and the density of the bowl are `1m` and `2 xx 10^(4) kg//m^(3)` respectively, then the inner diameter of bowl will be
View SolutionIn making an alloy, a substance of specific gravity `s_(1)` and mass `m_(1)` is mixed with another substance of specific gravity of the alloy is
View SolutionA concrete sphere of radius `R` has cavity of radius `r` which is packed with sawdust. The specific gravities of concrete and sawdust are respectively `2.4 and 0.3` for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of swadust will be
View SolutionA vessel contains oil (density `=13.6 gm//cm^3`). A uniform sphere floats with half its volume immersed in mercury and the other half in oil. The density of the material of sphere in `gm//cm^3` is:
View SolutionA body floats in a liquid contained in a beaker. The whole system as shown falls freely under gravity. The upthrust on the body due to the liquid is

View SolutionIf a block of iron (density `5 g cm^(-3))` is size 5 cm x 5 cm x 5 cm was weight while completely submerged in water, what would be the apparent weight ?
View SolutionA wooden block of volume `1000cm^(3)` is suspended from a spring balance its weight is 12 N in air. It is suspended in water such that half of the block is below the surface of water. The reading of spring balance is
View SolutionAn iceberg is floating partially immersed in sea water the density of sea water is 1.03 `gm//cm^(3)` and that of ice is `0.92gm//cm^(3)` what is the fraction of the total volume of the iceberg above the level of sea-water?
View SolutionA cubical block is floating in a liquid with half of its volume immersed in the liquid. When the whole system accelerates upwards with acceleration of `g//3`, the fraction of volume immersed in the liquid will be

View SolutionA silver ingot weighing 2.1 kg is held by a string so s to be completely immersed in a liquid of relative density `0.8`. The relative density of silver is `10.5`. The tension in the string in `kg-wt` is
View SolutionA sample of metal weights 210 grams in air 180 grams n water and 120 grams in an unknown liquid then
View SolutionTwo solids `A` and `B` floats in water. It is observed that `A` floats with half of its volume immersed and `B` Floats with `2//3` of its volume immersed. The ratio of densities of `A` and `B` is
View SolutionThe fraction of a floating object of volume `V_(0)` and density `d_(0)` above the surface of a liquid of density d will be
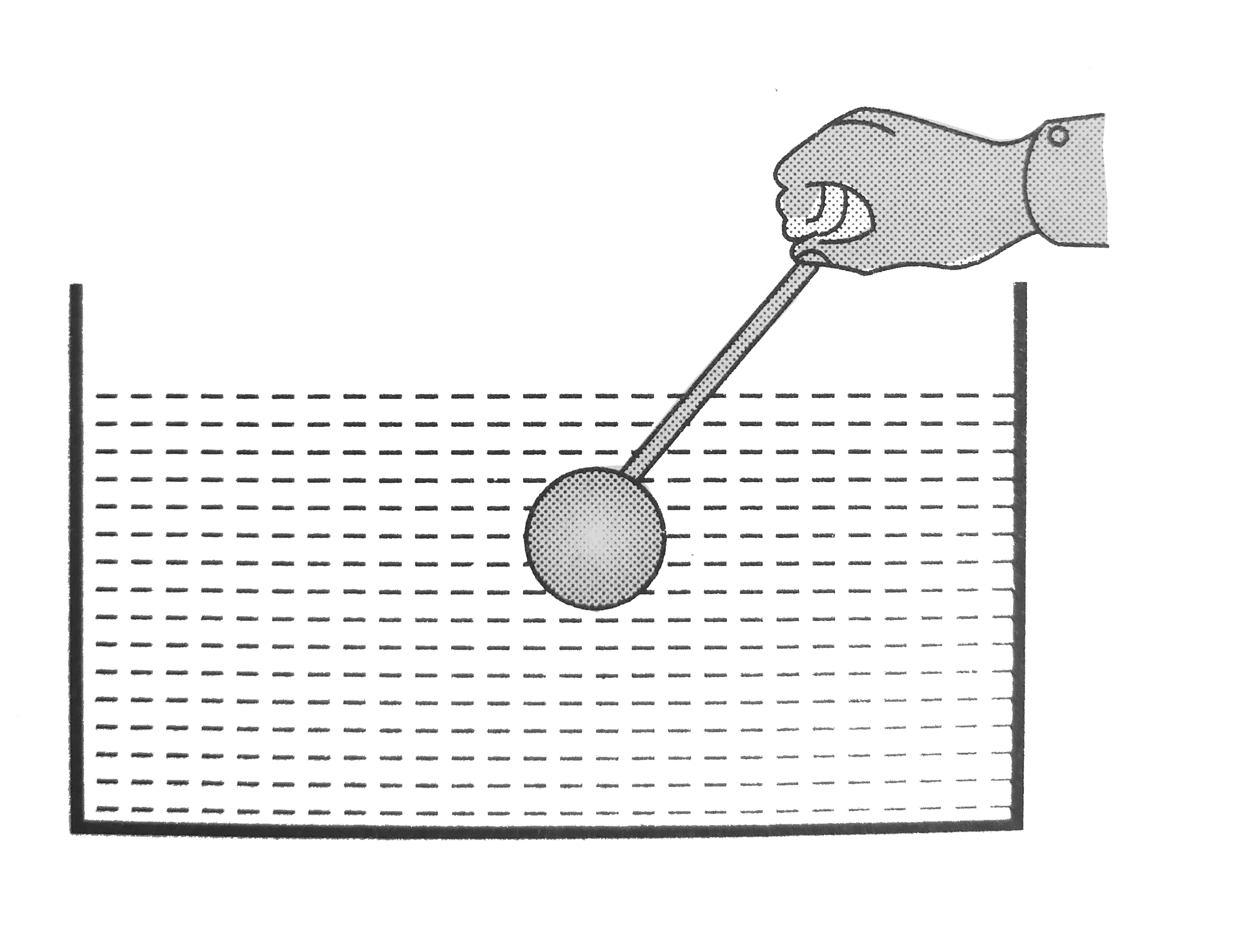
View SolutionA vessel with water is placed on a weighing pan and reads `600g`. Now a ball of 40g and density `0.80g//c c` is sunk into the water with a pin as shown in fig. keeping it sunk. The weighing pan will show a reading
View SolutionTwo water pipes of diameters 2 cm and 4 cm are connected with the main supply line. The velocity of flow of water in the pipe of 2 cm
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View SolutionWater enters through end A with a speed `v_1` and leaves through end B with a speed `v_2` of cylindrical tube AB. The tube is always completely filled with water. In case I the tube is horizontal, in case II it vertical with the end A upward and in case III it is vertical with the end B upward. We have `v_1=v_2`for
View SolutionWater is moving with a speed of `5.18 ms^(-1)` through a pipe with a cross-sectional area of `4.20 cm^2`. The water gradually descends `9.66 m` as the pipe increase in area to `7.60 cm^2`. The speed of flow at the lower level is
View SolutionThe velocity of kerosene oil in a horizontal pipe is `5 m//s`. If `g = 10m//s^(2)` then the velocity head of oil wlill be
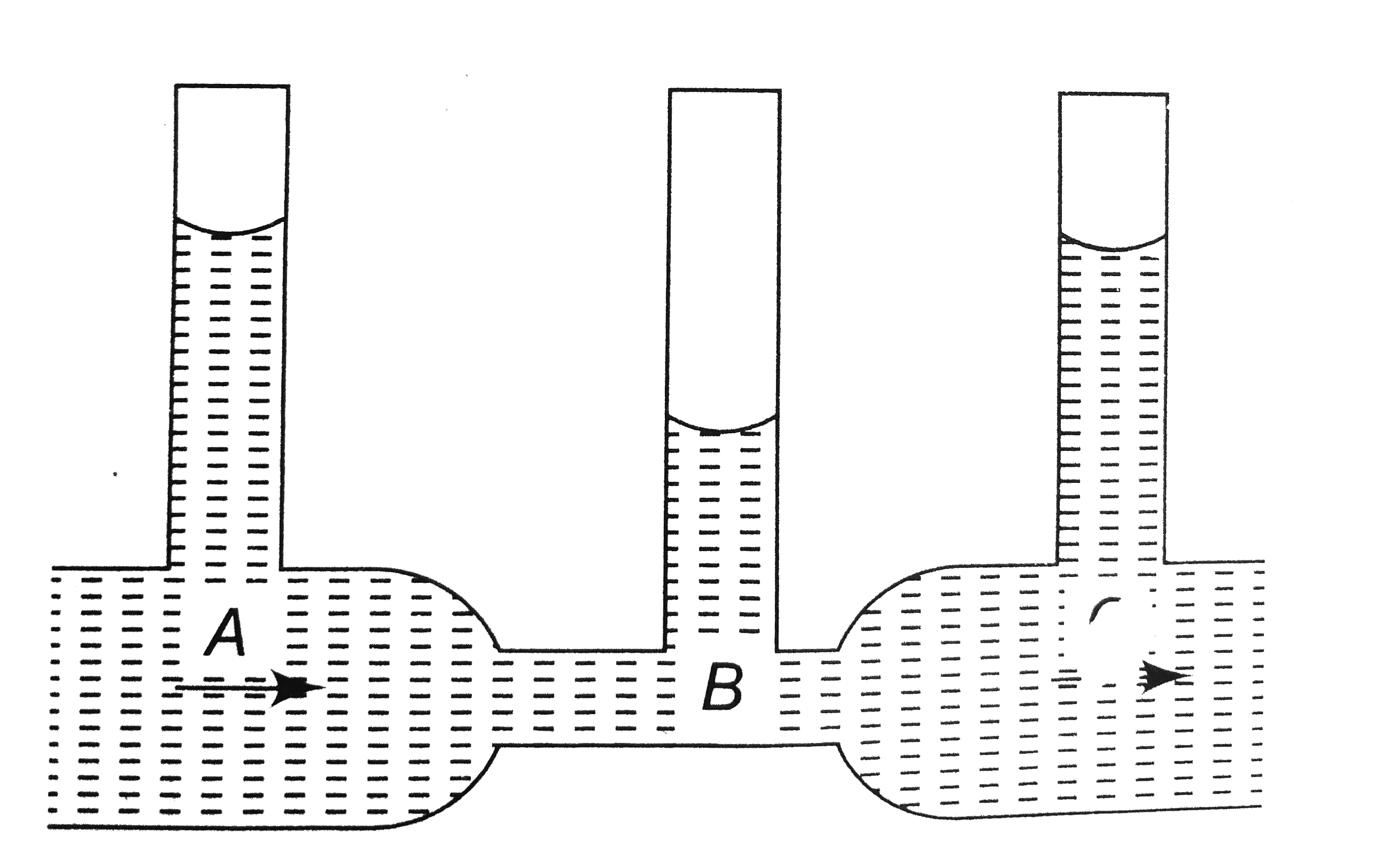
View SolutionIn the following fig., the flow of liquid through a horizontal pipe is shown. Three tubes A, B and C are connected to the pipe. The radii of the tubes `A,B and C` at the junction are respectively `2 cm, 1 cm and 2 cm`. It can be said that the
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is `r` and angular velocity of rotation is `omega`, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA manometer connected to a closed tap reads `3.5xx10^(5)N//m^(2)`.When the value is opened, the reading of manometer fall is `3.0xx10^(5)N//m^(2)`, then velocity of flow of water is
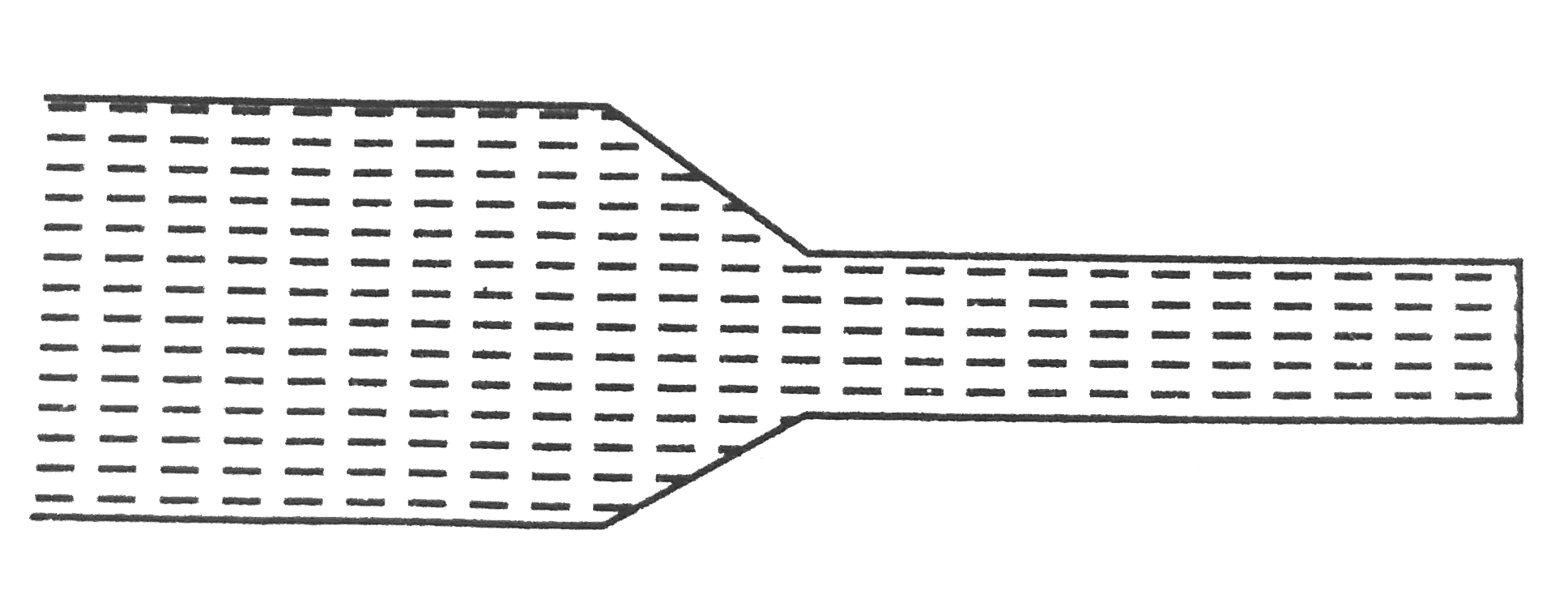
View SolutionWater flows through a frictionless duct with a cross-section varying as shown in fig. Pressure `p` at points along the axis is represented by
View SolutionAir is streaming past a horizontal airplane wing such that its speed is `90 ms^(-1)` at the lower surface and `120 ms^(-1)` over the upper surface. The wing is `10 m` long and has an average width of `2 m`, the difference of pressure on the two sides and the gross lift on the wing respectively, are (density of air `=1.3kgm^(-3)`)
View SolutionA large tank filled with water to a height `h` is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to `(h)/(2)` and from `(h)/(2)` to zero is
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water `(in ms^(-1))` through a small hole on the side wall of the cylinder near its bottom is
View SolutionThere is a small hole at the bottom of tank filled with water. If total pressure at the bottom is `3 atm(1 atm=10^(5)Nm^(-2))`, then find the velocity of water flowing from hole.
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionThere is a hole at the bottom of a large open vessel. If water is filled upto a height h, it flows out in time t. if water is filled to a height 4h, it will flow out in time
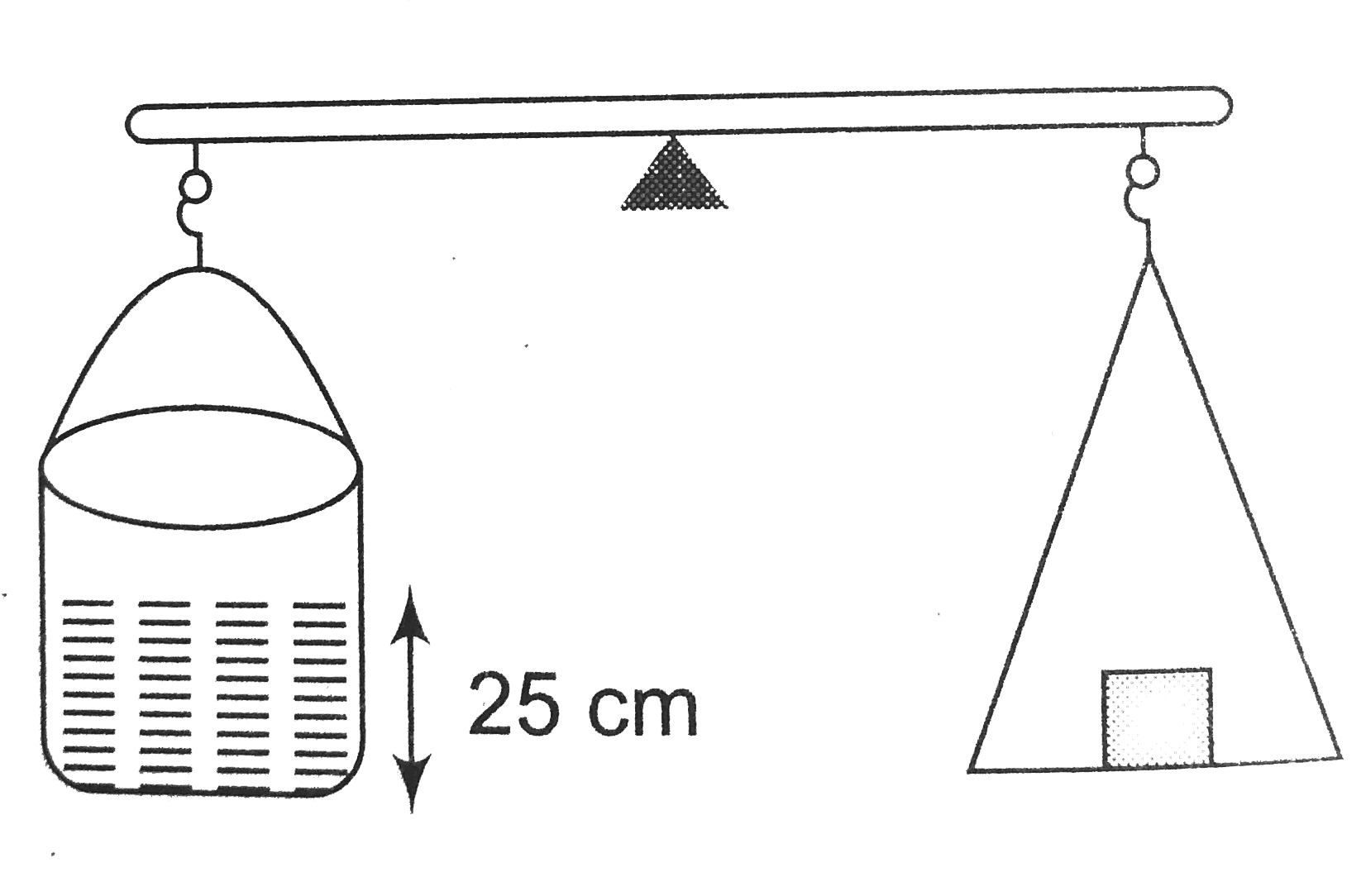
View SolutionA cylinder containing water up to a height of `25cm` has a hole of cross-section `1/4 cm^(2)` in its bottom. It is counterpoised in a balance. What is the initial change in the balancing weight when water begin to flow out?
View SolutionA cylindrical tank has a hole of 1 cm in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of `70 cm//sec` . then the maximum height up to which water can rise in the tank is
View SolutionA square plate of 0.1 m side moves parallel to a second plate with a velocity of `0.1 m//s`, both plates being immersed in water. If the viscous force is 0.002 N and the coefficient of viscosity is 0.01 poise , distance between the plates in m is
View Solution
The diagram shows a cup of tea seen from above. The tea has been stirred and is now rotating without turbulence. A graph showing the speed `v` with which the liquid is crossing points at a distance `X` from `O` along a radius `OX` would took like
View SolutionSpherical balls of radius 'R' are falling in a viscous fluid of viscosity `'eta'` with a velocity 'v'. The retarding viscous force acting on the spherical ball is
View SolutionA small sphere of mass m is dropped from a height After it has fallen 100 m it has attained its terminal velocity and continues to fall at that speed. The work done by air friction against the sphere during the first 100 m of fall is-
View SolutionTwo drops of the same radius are falling through air with a steady velcoity of `5 cm s^(-1).` If the two drops coalesce, the terminal velocity would be
View SolutionA ball of radius r and density r falls freely under gravity through a distance h before entering water. Velocity of ball does not change even on entering water. If viscosity of water is `eta` the value of h is given by
` (##DPP_PHY_CP09_E01_002_Q01.png" width="80%">
View SolutionThe rate of steady volume flow of water through a capillary tube of length ' l ' and radius ' r ' under a pressure difference of P is V . This tube is connected with another tube of the same length but half the radius in series. Then the rate of steady volume flow through them is (The pressure difference across the combination is P )
View SolutionA liquid is flowing in a horizontal uniform capillary tube under a constant pressure difference P . The value of pressure for which the rate of flow of the liquid is doubled when the radius and length both are doubled is
View SolutionTwo capillary tubes of same radius `r` but of lengths `l_(1)` and `l_(2)` are fitted in parallel to the bottom of a vessel. The pressure to the bottom of a vessel. The pressure head is P. What should be the length of a single tube of same radius that can replace the two tubes so that the rate of flow is same as before?
View SolutionWe have two (narrow) capillary tubes T and T . Their lengths are l and l and radii of cross-section are r and r respectively. The rate of flow of water under a pressure difference P through tube T is `8 cm 3// sec`. If `l = 2l` and `r = r` what will be the rate of flow when the two tubes are connected in series and pressure difference across the combinatin is same as before `(= P)`
View SolutionA capillary tube is attached horizontally to a constant pressure head arrangement. If the radius of the capillary tube is increased by `10%`, then the rate of flow of the liquid shall change nearly by
View SolutionA wooden stick 2m long is floating on the surface of water. The surface tension of water 0.07 N/m. By putting soap solution on one side of the sticks the surface tension is reduced to 0.06 N/m. The net force on the stick will be
View SolutionA thin metal disc of radius `r` floats on water surface and bends the surface downwards along the perimeter making an angle `theta` with vertical edge of the disc. If the disc displaces a weight of water `W` and surface tension of water is `T`, then the weight of metal disc is :
View SolutionA 10 cm long wire is placed horizontal on the surface of water and is gently pulled up with a force of `2xx10^(2)` N to keep the wire in equilibrium. The surface tension, in `Nm^(-1)` of water is
View SolutionThere is a howizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius `R`. If the surface tension of the loop be `T`, then what will be the tension in the thread?
View SolutionA liquid is filled into a semi elliptical cross section with a as semi major axis and b as semi minor axis. The ratio of surface tension forces on the curved part and the plane part of the tube in vertical position will be
View Solution`A` liquid film is formed over a frame `ABCD` as shown in figure. Wire `CD` can slide without friction. The mass to be hung from `CD` to keep it in equilibrium is

View SolutionTwo small drops of mercury, each of radius `R`, coalesce to form a single large drop. The ratio of the total surface energies before and after the change is
View SolutionRadius of a soap bubble is increased from R to 2 R work done in this process in terms of surface tension is
View SolutionThe work done in blowing a soap bubble of 10 cm radius is (Surface tension of the soap solution is `3/100` N/m)
View SolutionA drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury `=0.465Jm^-2`
View SolutionThe work done in increasing the size of a soap film from `10cmxx6cm` to `10cmxx11cm` is `3xx10^-4` Joule. The surface tension of the film is
View SolutionA film of water is formed between two straight parallel wires of length 10 cm each separated by `0.5cm` If their separation is increased by `1mm` while still maintaining their parallelism, how much work will have to be done (Surface tension of water `=7.2xx10^-2(N)/(m)`)
View SolutionThe work done in blowing a bubble of volume `V` is `W`, then what is the work done in blowing a soap bubble of volume `2V` ?
View SolutionSeveral spherical drops of a liquid of radius `r` coalesce to form a single drop of radius `R`. If `T` is surface tension and `V` is volume under consideration, then the release of energy is
View SolutionThe pressure inside a small air bubble of radius `0.1mm` situated just below the surface of water will be equal to `("Take surface tension of water" 70xx10^(-3)1^(J)m^(-1) "and atmospheric pressure" =1.013xx10^(5)Nm^(-2))`
View SolutionIf the radius of a soap bubble is four times that of another, then the ratio of their pressures will be
View SolutionPressure inside two soap bubbles are `1.01` and `1.02` atmospheres. Ratio between their volumes is
View SolutionThe excess pressure inside an air bubble of radius `r` just below the surface of water is `P_(1)`. The excess pressure inside a drop of the same radius just outside the surface is `P_(2)`. If `T` is surface tension then
View SolutionWater rises in a capillary tube to a height 2.0 cm. In an another capillary tube whose radius is one third of it, how much the water will rise ? If the first capillary tube is inclined at an angle of `60^@` with the vertical then what will be the position of water in the tube.
View SolutionTwo capillary tubes of same diameter are put vertically one each in two liquids whose relative densities are 0.8 and 0.6 and surface tensions are 60 dyne/cm and 50 dyne/cm respectively. Ratio of heights of liquids in the two tubes `(h_(1))/(h_(2))` is
View SolutionA capillary tube of radius R is immersed in water and water rises in it to a height H . Mass of water in the capillary tube is . M If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be
View SolutionWater rises to a height `h` in a capillary at the surface of earth. On the surface of the moon the height of water column in the same capillary will be-
View SolutionIf the surface tension of water is 0.06 Nm, then the capillary rise in a tube of diameter 1mm is `(theta=0^(@)`)
View SolutionTwo capillaries made of same material but of different radii are dipped in a liquid. The rise of liquid in one capillary is 2.2 cm and that in the other is 6.6 cm . The ratio of their radii is
View SolutionThe lower end of a capillary tube is at a depth of `12 cm` and water rises `3 cm` in it. The mouth pressure required to blow an air bubble at the lower end will be `x cm` of water column, where `x` is
View SolutionThe lower end of a capillary tube of radius r is placed vertically in water of density `rho` , surface tension S. The rice of water in the capillary tube is upto height h, then heat evolved is
View SolutionWater rises in a capillary tube to a certain height such that the upward force due to surface tension is balanced by `75xx10^-4` newton force due to the weight of the liquid. If the surface tension of water is `6xx`10^-2` newton/metre the inner circumference of the capillary must be:
View SolutionThe radii of two soap bubbles are `r_(i)` and `r_(2)`. In isothermal conditions, two meet together in vacuum. Then the radius kof the resultant bubble is given by
View SolutionTwo soap bubbles of radii `r_(1)` and `r_(2)` equal to 4 cm and 5 cm are touching each other over a common surface `S_(1)S_(2)` (shown in figure). Its radius will be
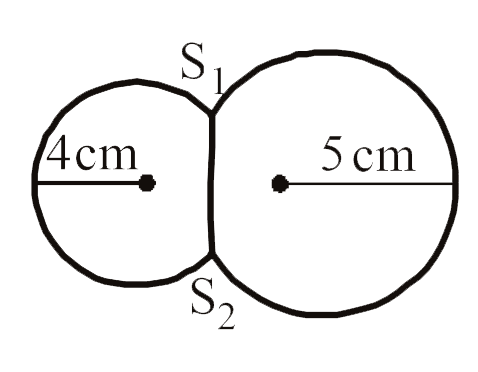
View SolutionAn air bubble in a water tank rises from the bottom to the top. Which of the following statements are true?
View SolutionThe radii of two soap bubbles are `R_(1)` and `R_(2)` respectively. The ratio of masses of air in them will be
View SolutionOn dipping one end of a capiilary in liquid and inclining the capillary at an angles `30^(@)` and `60^(@)` with the vertical, the lengths of liquid columns in it are found to be `l_(1)` and `l_(2)` respectively. The ratio of `l_(1)` and `l_(2)` is
View Solution`A` drop of water of volume `V` is pressed between the two glass plates so as to spread to an area. `A`. If `T` is the surface tension, the normal force required to separate the glass plates is
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter FLUID MECHANICS of BANSAL PHYSICS (HINGLISH) of Class 12