Complete Solutions to बहुवैकल्पिक प्रश्न of chapter बोध - संबध्द प्रकार के प्रश्न of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | बोध - संबध्द प्रकार के प्रश्न |
| BHARATI BHAWAN | बहुवैकल्पिक प्रश्न |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
स्थिर वैद्युतिकी (electrostatics) में गॉस के प्रमेय का अनुप्रयोग जिस प्रकार किया जाता हैं , ठीक उसी प्रकार गुरुत्वाकर्षण (gravitation) संबंधी प्रश्नों का हल भी गॉस के प्रमेय के अनुप्रयोग से संभव हैं , क्योंकि दोनों प्रकार के बलों के लिए व्युत्क्रम - वर्ग नियम ( inverse square law ) मान्य हैं । इसके अतिरिक्त निम्नलिखित समतुल्यताओं की मान्यता भी आवश्यकता हैं :
(i) आवेश (charge) - द्रव्यमान (mass)
(ii) विद्युत - क्षेत्र की प्रबलता - गुरुत्वीय क्षेत्र की तीव्रता अथवा गुरुत्वीय त्वरण
(iii) नियतांक , k = `(1)/(4 pi in_(0))` - गुरुत्वाकर्षण नियतांक G
अनंत विस्तार की एक पतली एकसमान समतल प्लेट ( जिसके प्रति एकांक क्षेत्रफल का द्रव्यमान m हैं ) के निकट गुरुत्वीय क्षेत्र की प्रबलता का परिमाण03:55View Solutionस्थिर वैद्युतिकी (electrostatics) में गॉस के प्रमेय का अनुप्रयोग जिस प्रकार किया जाता हैं , ठीक उसी प्रकार गुरुत्वाकर्षण (gravitation) संबंधी प्रश्नों का हल भी गॉस के प्रमेय के अनुप्रयोग से संभव हैं , क्योंकि दोनों प्रकार के बलों के लिए व्युत्क्रम - वर्ग नियम ( inverse square law ) मान्य हैं । इसके अतिरिक्त निम्नलिखित समतुल्यताओं की मान्यता भी आवश्यकता हैं :
(i) आवेश (charge) - द्रव्यमान (mass)
(ii) विद्युत - क्षेत्र की प्रबलता - गुरुत्वीय क्षेत्र की तीव्रता अथवा गुरुत्वीय त्वरण
(iii) नियतांक , k = `(1)/(4 pi in_(0))` - गुरुत्वाकर्षण नियतांक G
पृथ्वी के भीतर केंद्र से r दूरी पर गुरुत्वीय त्वरण का मान `(gr)/(R)` होता हैं , जहाँ g = पृथ्वी की सतह पर गुरुत्वीय त्वरण तथा R = पृथ्वी की त्रिज्या हैं । इसी प्रकार , Q आवेश युक्त R त्रिज्या के परावैद्युत गोले के भीतर केंद्र से r दूरी पर विद्युत - क्षेत्र का परिमाण होगा ( मान लें कि आवेश का वितरण संपूर्ण गोले के आयतन में एकसमान रुप से वितरित हैं )03:13View Solutionस्थिर वैद्युतिकी (electrostatics) में गॉस के प्रमेय का अनुप्रयोग जिस प्रकार किया जाता हैं , ठीक उसी प्रकार गुरुत्वाकर्षण (gravitation) संबंधी प्रश्नों का हल भी गॉस के प्रमेय के अनुप्रयोग से संभव हैं , क्योंकि दोनों प्रकार के बलों के लिए व्युत्क्रम - वर्ग नियम ( inverse square law ) मान्य हैं । इसके अतिरिक्त निम्नलिखित समतुल्यताओं की मान्यता भी आवश्यकता हैं :
(i) आवेश (charge) - द्रव्यमान (mass)
(ii) विद्युत - क्षेत्र की प्रबलता - गुरुत्वीय क्षेत्र की तीव्रता अथवा गुरुत्वीय त्वरण
(iii) नियतांक , k = `(1)/(4 pi in_(0))` - गुरुत्वाकर्षण नियतांक G
प्रति एकांक लंबाई के द्रव्यमान `lamda` युक्त किसी पतले एकसमान धागे के कारण r दूरी पर गुरुत्वीय क्षेत्र की प्रबलता का परिमाण05:30View Solutionविद्युत - क्षेत्र `vec(E)` में आवेश q पर आरोपित बल `vec(F)` परिणामी एंव दिशा में सूत्र `vec(F) = q vec(E)` व्दारा व्यक्त होता हैं । आरोपित बल की दिशा आवेश की प्रकृति ( धनात्मक एंव ऋणात्मक ) पर निर्भर करती हैं । स्प्ष्टतः , किसी एकसमान विद्युत - क्षेत्र ( uniform electric field ) में विराम में स्थित मुक्त आवेश क्षेत्र `vec(E)` की दिशा के समांतर अथवा विपरीत दिशा में सरल रेखा में गतिशील होता हैं । यदि कोई गतिशील आवेशित कण विद्युत - क्षेत्र की दिशा के साथ कोण `theta`बनाता हुआ क्षेत्र में प्रवेश करता हो तब इसका गति पथ परवलीय (parabolic) होता हैं , यदि `theta ne 0^(@) , 180^(@)`.
इसी क्रम में क्षैतिज दिशा में गतिशील प्रोटॉन पर विचार करें जो समय t = 0 पर एकसमान ऊर्ध्वाधर विद्युत - क्षेत्र (uniform vertical electric field) में प्रवेश कर रहा हो । प्रवेश करते समय जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन तक आने में लगा समय , क्षेत्र की अनुपस्थिति में लगनेवाले समय का आधा हैं । यह भी पाया जाता हैं कि क्षेत्र के अंदर प्रोटॉन व्दारा ` 250 mu s ` ( माइक्रोसेकंड) में 10 cm का क्षैतिज विस्थापन होता हैं और अंततः यह ` 500 m s^(-1)` की चाल से जमीन से टकराता हैं ।
विद्युत - क्षेत्र `vec(E)` की दिशा हैं05:56View Solutionविद्युत - क्षेत्र `vec(E)` में आवेश q पर आरोपित बल `vec(F)` परिणामी एंव दिशा में सूत्र `vec(F) = q vec(E)` व्दारा व्यक्त होता हैं । आरोपित बल की दिशा आवेश की प्रकृति ( धनात्मक एंव ऋणात्मक ) पर निर्भर करती हैं । स्प्ष्टतः , किसी एकसमान विद्युत - क्षेत्र ( uniform electric field ) में विराम में स्थित मुक्त आवेश क्षेत्र `vec(E)` की दिशा के समांतर अथवा विपरीत दिशा में सरल रेखा में गतिशील होता हैं । यदि कोई गतिशील आवेशित कण विद्युत - क्षेत्र की दिशा के साथ कोण `theta`बनाता हुआ क्षेत्र में प्रवेश करता हो तब इसका गति पथ परवलीय (parabolic) होता हैं , यदि `theta ne 0^(@) , 180^(@)`.
इसी क्रम में क्षैतिज दिशा में गतिशील प्रोटॉन पर विचार करें जो समय t = 0 पर एकसमान ऊर्ध्वाधर विद्युत - क्षेत्र (uniform vertical electric field) में प्रवेश कर रहा हो । प्रवेश करते समय जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन तक आने में लगा समय , क्षेत्र की अनुपस्थिति में लगनेवाले समय का आधा हैं । यह भी पाया जाता हैं कि क्षेत्र के अंदर प्रोटॉन व्दारा ` 250 mu s ` ( माइक्रोसेकंड) में 10 cm का क्षैतिज विस्थापन होता हैं और अंततः यह ` 500 m s^(-1)` की चाल से जमीन से टकराता हैं ।
प्रोटॉन के जमीन से टकराने में लगा समय12:13View Solutionविद्युत - क्षेत्र `vec(E)` में आवेश q पर आरोपित बल `vec(F)` परिणामी एंव दिशा में सूत्र `vec(F) = q vec(E)` व्दारा व्यक्त होता हैं । आरोपित बल की दिशा आवेश की प्रकृति ( धनात्मक एंव ऋणात्मक ) पर निर्भर करती हैं । स्प्ष्टतः , किसी एकसमान विद्युत - क्षेत्र ( uniform electric field ) में विराम में स्थित मुक्त आवेश क्षेत्र `vec(E)` की दिशा के समांतर अथवा विपरीत दिशा में सरल रेखा में गतिशील होता हैं । यदि कोई गतिशील आवेशित कण विद्युत - क्षेत्र की दिशा के साथ कोण `theta`बनाता हुआ क्षेत्र में प्रवेश करता हो तब इसका गति पथ परवलीय (parabolic) होता हैं , यदि `theta ne 0^(@) , 180^(@)`.
इसी क्रम में क्षैतिज दिशा में गतिशील प्रोटॉन पर विचार करें जो समय t = 0 पर एकसमान ऊर्ध्वाधर विद्युत - क्षेत्र (uniform vertical electric field) में प्रवेश कर रहा हो । प्रवेश करते समय जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र `vec(E)` की उपस्थिति में प्रोटॉन को जमीन तक आने में लगा समय , क्षेत्र की अनुपस्थिति में लगनेवाले समय का आधा हैं । यह भी पाया जाता हैं कि क्षेत्र के अंदर प्रोटॉन व्दारा ` 250 mu s ` ( माइक्रोसेकंड) में 10 cm का क्षैतिज विस्थापन होता हैं और अंततः यह ` 500 m s^(-1)` की चाल से जमीन से टकराता हैं ।
जमीन से टकराते समय प्रोटॉन के वेग का ऊर्ध्वाधर घटक (vertical component ) हैं ।06:27View Solutionकिसी गोले की त्रिज्या R है तथा इसके पदार्थ की परावैद्युतता (permittivity ) `in` हैं । इसके भीतर आवेश का आयतन - घनत्व ( volume density of charge) `rho` को गोले के केंद्र से दूरी r के फलन ( function ) के रुप में संबंध `rho = rho_(0)(1 - (r)/(R))` से व्यक्त किया जाता हैं ।
केंद्र से दूरी के फलन के रुप में गोले के भीतर विद्युत - क्षेत्र का परिमाण हैं05:14View Solutionकिसी गोले की त्रिज्या R है तथा इसके पदार्थ की परावैद्युतता (permittivity ) `in` हैं । इसके भीतर आवेश का आयतन - घनत्व ( volume density of charge) `rho` को गोले के केंद्र से दूरी r के फलन ( function ) के रुप में संबंध `rho = rho_(0)(1 - (r)/(R))` से व्यक्त किया जाता हैं ।
केंद्र से दूरी r के फलन के रुप में गोले के बाहर विद्युत - क्षेत्र का परिमाण हैं05:14View Solutionकिसी गोले की त्रिज्या R है तथा इसके पदार्थ की परावैद्युतता (permittivity ) `in` हैं । इसके भीतर आवेश का आयतन - घनत्व ( volume density of charge) `rho` को गोले के केंद्र से दूरी r के फलन ( function ) के रुप में संबंध `rho = rho_(0)(1 - (r)/(R))` से व्यक्त किया जाता हैं ।
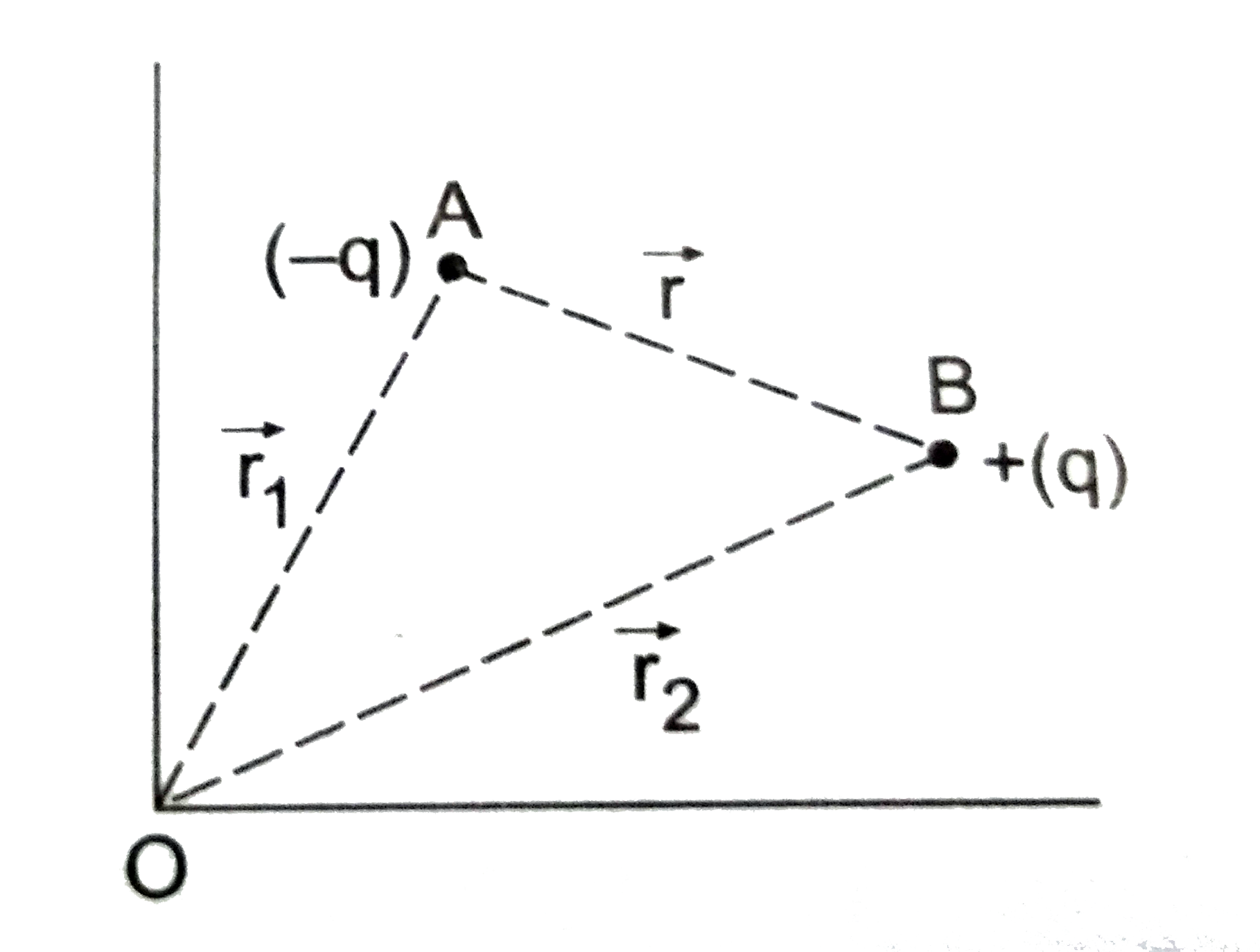
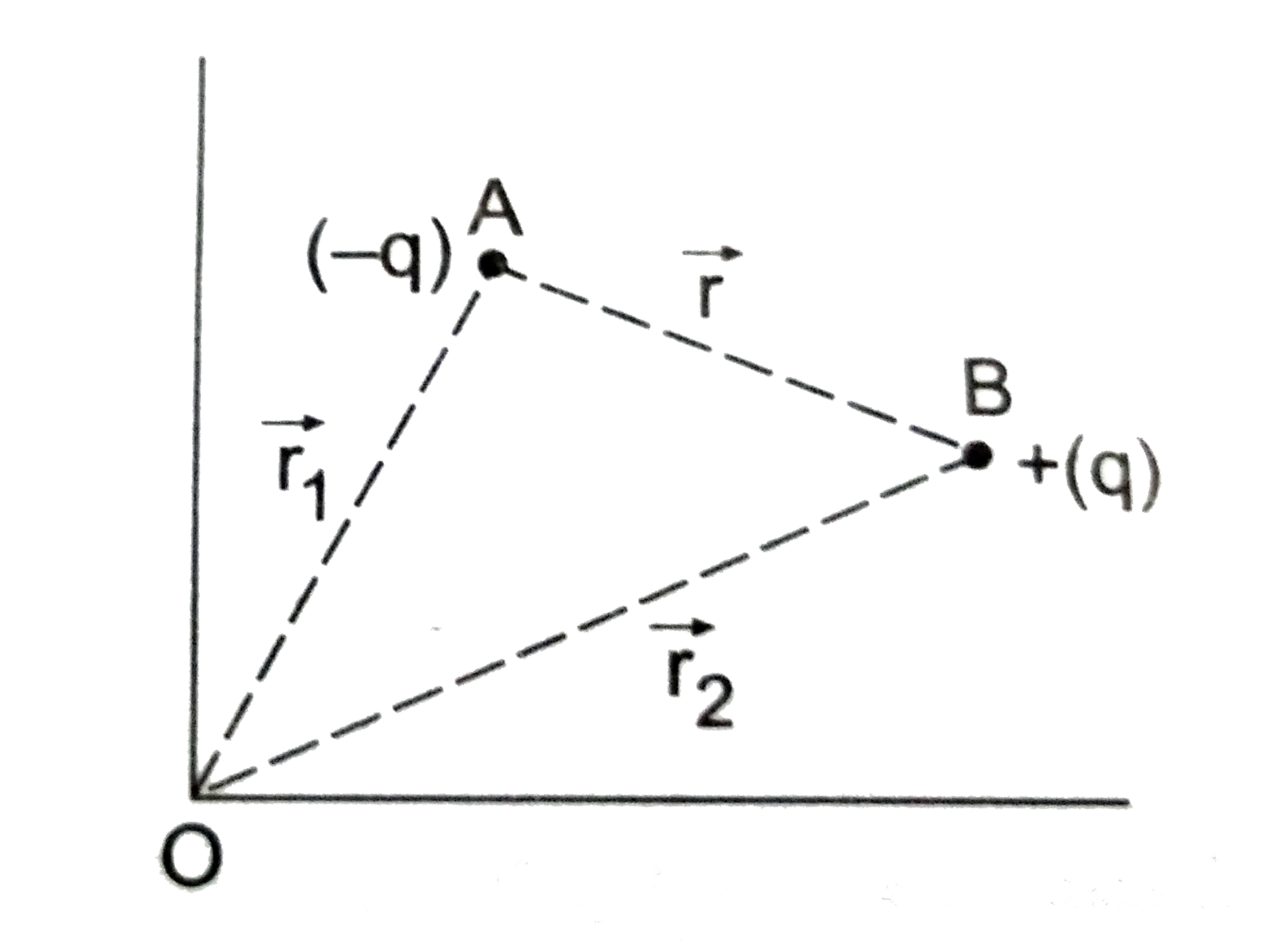
केंद्र से वह दूरी `r_(m)` जहाँ पर विद्युत - क्षेत्र का परिमाण महत्तम हैं06:28View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से `(-q)vec(r_(1)) + (+ q) vec(r_(2)) = q(vec r_(2) - vec(r_(1))) = q vec(r) = vec (P)` = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , `vec(P) = sum vec(r_(i) q_(i)) तथा आवेश के संतत ( continuous) वितरण के लिए , `vec(P) = int vec(r_(i))dq_(i).`
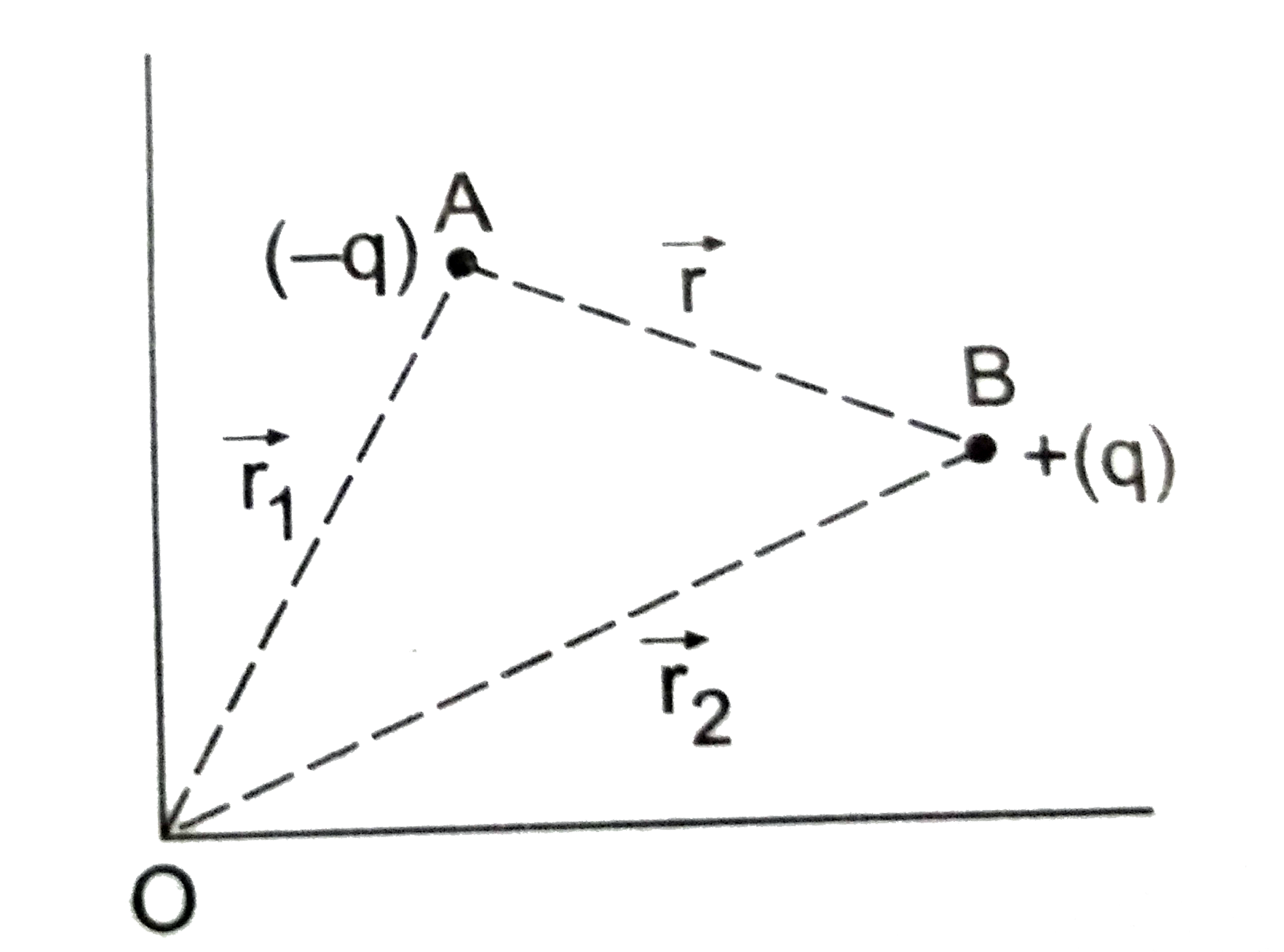
तीन आवेशों से बने किसी निकाय का व्दिध्रुम - आघूर्ण ज्ञात करें जिसमें आवेश `1 mu C` की स्थिति ( 3Å , 0 , 0) , आवेश `2 mu C` की स्थिति (0, 2 Å , 0 ) तथा ` - 3mu C` आवेश की स्थिति (0,0 , -1 Å) पर हो ।05:28View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से `(-q)vec(r_(1)) + (+ q) vec(r_(2)) = q(vec r_(2) - vec(r_(1))) = q vec(r) = vec (P)` = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , `vec(P) = sum vec(r_(i) q_(i))` तथा आवेश के संतत ( continuous) वितरण के लिए , `vec(P) = int vec(r_(i))dq_(i)`
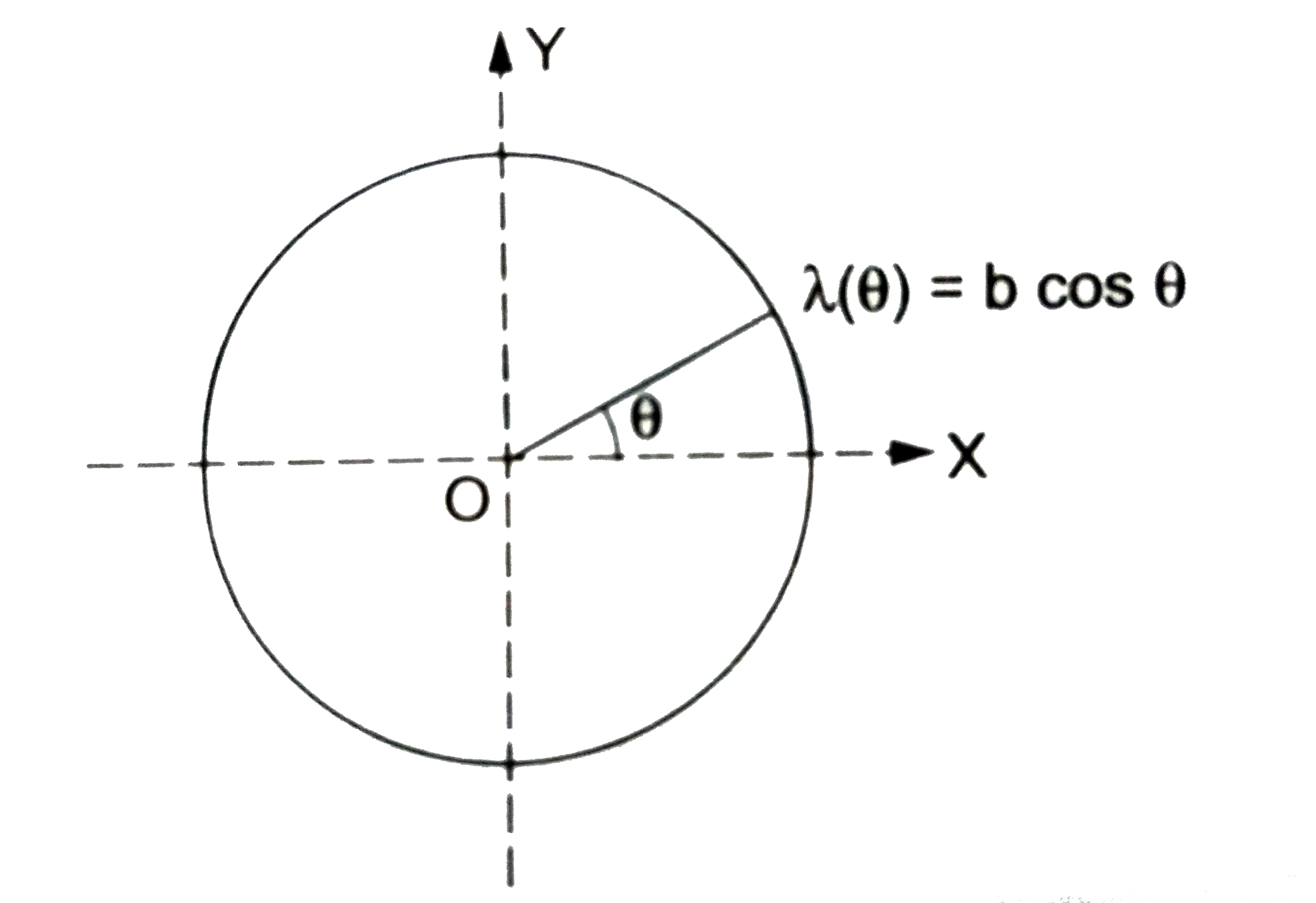
XY - तल में स्थित त्रिज्या R के एक आवेशित रिंग का केंद्र - मूलबिंदु o पर स्थित हैं तथा इसके आवेश का रैखिक घनत्व `lamda`, कोण `theta` के फलन के रुप में संबंध `lamda (theta) = b cos theta` से व्यक्त होता हैं । आवेशित रिंग का विद्युत व्दिध्रुव - आघूर्ण हैं
 11:19View Solution
11:19View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से `(-q)vec(r_(1)) + (+ q) vec(r_(2)) = q(vec r_(2) - vec(r_(1))) = q vec(r) = vec (P)` = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , `vec(P) = sum vec(r_(i) q_(i))` तथा आवेश के संतत ( continuous) वितरण के लिए , `vec(P) = int vec(r_(i))dq_(i).`
उपर्युक्त आवेशित रिंग के कारण बिंदु P(nR, 0,0) पर विद्युत - क्षेत्र ज्ञात करें , जहाँ n का मान बहूत बड़ा हैं ।View Solutionएक समांतर प्लेट संधारित्र की दोनों प्लेटों को ऊर्ध्वाधरतः रखकर दृढ़ आधार से क्लैम्प कर दिया गया हैं । दोनों प्लेट शून्य - विक्षेप प्रदर्शित करनेवाले गैलवेनोमीटर से होकर सेल व्दारा संबंधित हैं । धातु की बात एक समतल प्लेट जिसकी मोटाई संधारित्र की प्लेटों के बीच की दूरी से थोड़ा कम हैं , प्लेटों के बीच से होकर उन्हें बिना स्पर्श किए ऊर्ध्वाधरतः गुरुत्व के अधीन गिरती हैं ।
गैलवेनोमीटर के सूचक के विक्षेप का सही विवरण निम्नलिखित में किस विकल्प व्दारा व्यक्त होता हैं ?03:00View Solutionएक समांतर प्लेट संधारित्र की दोनों प्लेटों को ऊर्ध्वाधरतः रखकर दृढ़ आधार से क्लैम्प कर दिया गया हैं । दोनों प्लेट शून्य - विक्षेप प्रदर्शित करनेवाले गैलवेनोमीटर से होकर सेल द्वारा संबंधित हैं । धातु की एक समतल प्लेट जिसकी मोटाई संधारित्र की प्लेटों के बीच की दूरी से थोड़ा कम हैं , प्लेटों के बीच से होकर उन्हें बिना स्पर्श किए ऊर्ध्वाधरतः गुरुत्व के अधीन गिरती हैं ।
संधारित्र की प्लेटों के बीच से गुजरने के क्रम में धातु की प्लेट की गति का सही विवरण निम्नलिखित में किस विकल्प व्दारा व्यक्त होता हैं ?View Solutionएक समांतर प्लेट संधारित्र की दोनों प्लेटों को ऊर्ध्वाधरतः रखकर दृढ़ आधार से क्लैम्प कर दिया गया हैं । दोनों प्लेट शून्य - विक्षेप प्रदर्शित करनेवाले गैलवेनोमीटर से होकर सेल द्वारा संबंधित हैं । धातु की बात एक समतल प्लेट जिसकी मोटाई संधारित्र की प्लेटों के बीच की दूरी से थोड़ा कम हैं , प्लेटों के बीच से होकर उन्हें बिना स्पर्श किए ऊर्ध्वाधरतः गुरुत्व के अधीन गिरती हैं ।
धातु की प्लेट को संधारित्र की प्लेटों की बीच से गुजरने के संपूर्ण प्रक्रम में , निम्नलिखित विकल्पों में कौन सही नहीं हैं ?05:40View Solutionटेलीविजन , रेडियो जैसे इलेक्ट्रॉनिक साधनों के विद्युत - परिपथ की जाँच के क्रम में मल्टीमीटर का उपयोग किया जाता हैं । इस यंत्र में एक मिलीऐमीटर (milliameter) को विभिन्न प्रतिरोधों से जोड़कर विभिन्न परास (range) की धारा , विभवांतर तथा प्रतिरोधों का मापन किया जाता हैं । चित्र में मल्टीमीटर का परिपथ दिखाया गया हैं जिसके टर्मिनल P से धारा प्रवेश करती हैं और जो मिलीऐमीटर से तथा इसके श्रेणी तथा समांतरक्रम में जुड़े प्रतिरोधकों से प्रवाहित होकर अन्य किसी टर्मिनल Q , R ,S बाहर निकलती हैं । धारा को किस टर्मिनल से बाहर निकलना हैं यह इस बात पर निर्भर करता हैं कि मल्टीमीटर का उपयोग ऐमीटर , वोल्टमीटर या प्रतिरोध मापक के रुप में किस परास (range) के मापन के लिया किया जाना हैं । दिए गए चित्र में मिलीऐमीटर की कुंडली का प्रतिरोध `0.9 Omega ` तथा इससे 10 mA की धारा प्रवाहित होने पर यह पूर्ण स्केल विक्षेप ( full scale deflection ) देता हैं ।
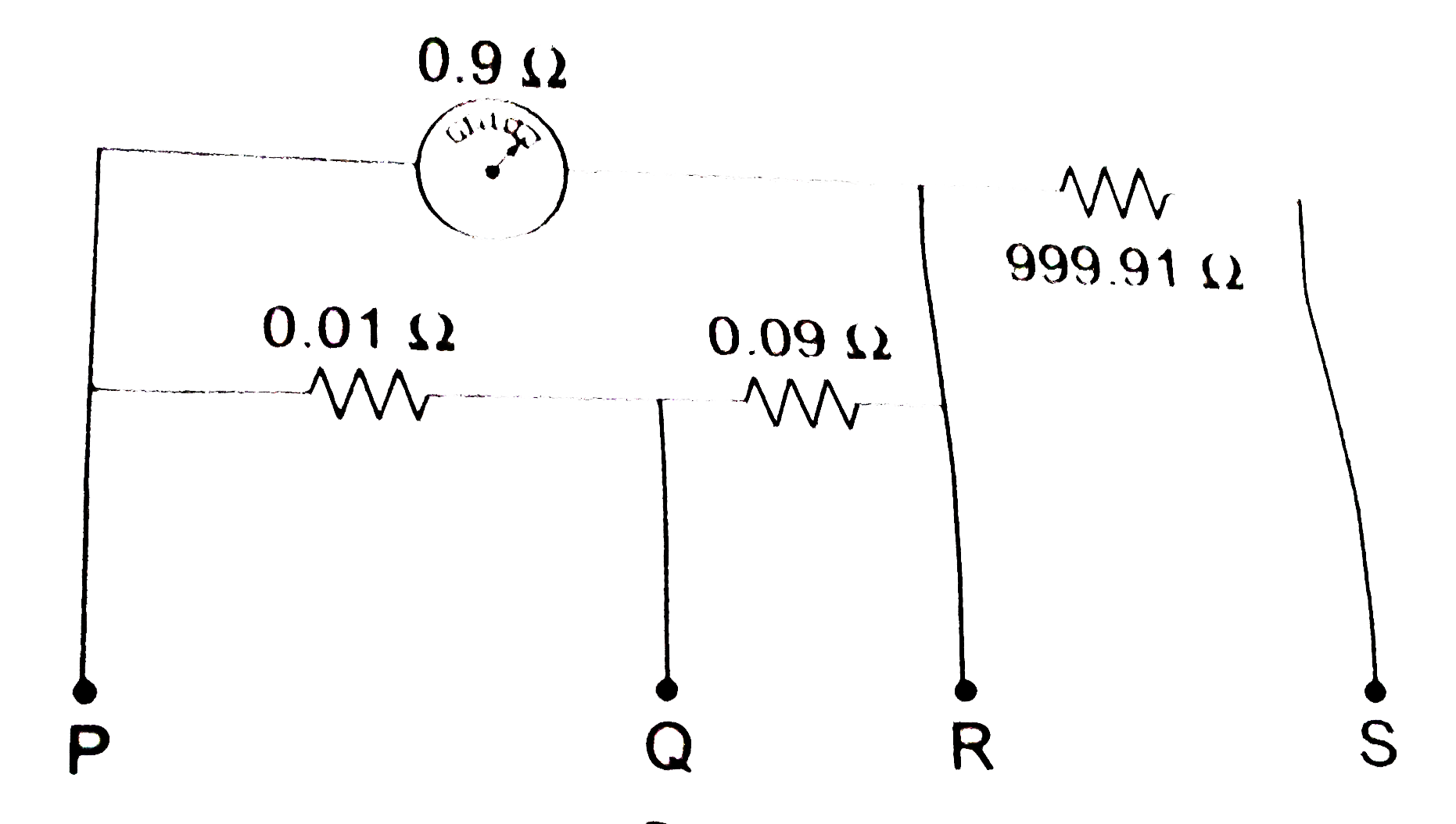
यदि मल्टीमीटर के टर्मिनल P तथा Q से क्रमशः धारा के प्रवेश तथा निकास हो , तब यह व्यवस्था एक ऐमीटर जैसा कार्य करेगी जिसका पारस हैं05:12View Solutionटेलीविजन , रेडियो जैसे इलेक्ट्रॉनिक साधनों के विद्युत - परिपथ की जाँच के क्रम में मल्टीमीटर का उपयोग किया जाता हैं । इस यंत्र में एक मिलीऐमीटर (milliameter) को विभिन्न प्रतिरोधों से जोड़कर विभिन्न परास (range) की धारा , विभवांतर तथा प्रतिरोधों का मापन किया जाता हैं । चित्र में मल्टीमीटर का परिपथ दिखाया गया हैं जिसके टर्मिनल P से धारा प्रवेश करती हैं और जो मिलीऐमीटर से तथा इसके श्रेणी तथा समांतरक्रम में जुड़े प्रतिरोधकों से प्रवाहित होकर अन्य किसी टर्मिनल Q , R ,S बाहर निकलती हैं । धारा को किस टर्मिनल से बाहर निकलना हैं यह इस बात पर निर्भर करता हैं कि मल्टीमीटर का उपयोग ऐमीटर , वोल्टमीटर या प्रतिरोध मापक के रुप में किस परास (range) के मापन के लिया किया जाना हैं । दिए गए चित्र में मिलीऐमीटर की कुंडली का प्रतिरोध `0.9 Omega ` तथा इससे 10 mA की धारा प्रवाहित होने पर यह पूर्ण स्केल विक्षेप ( full scale deflection ) देता हैं ।
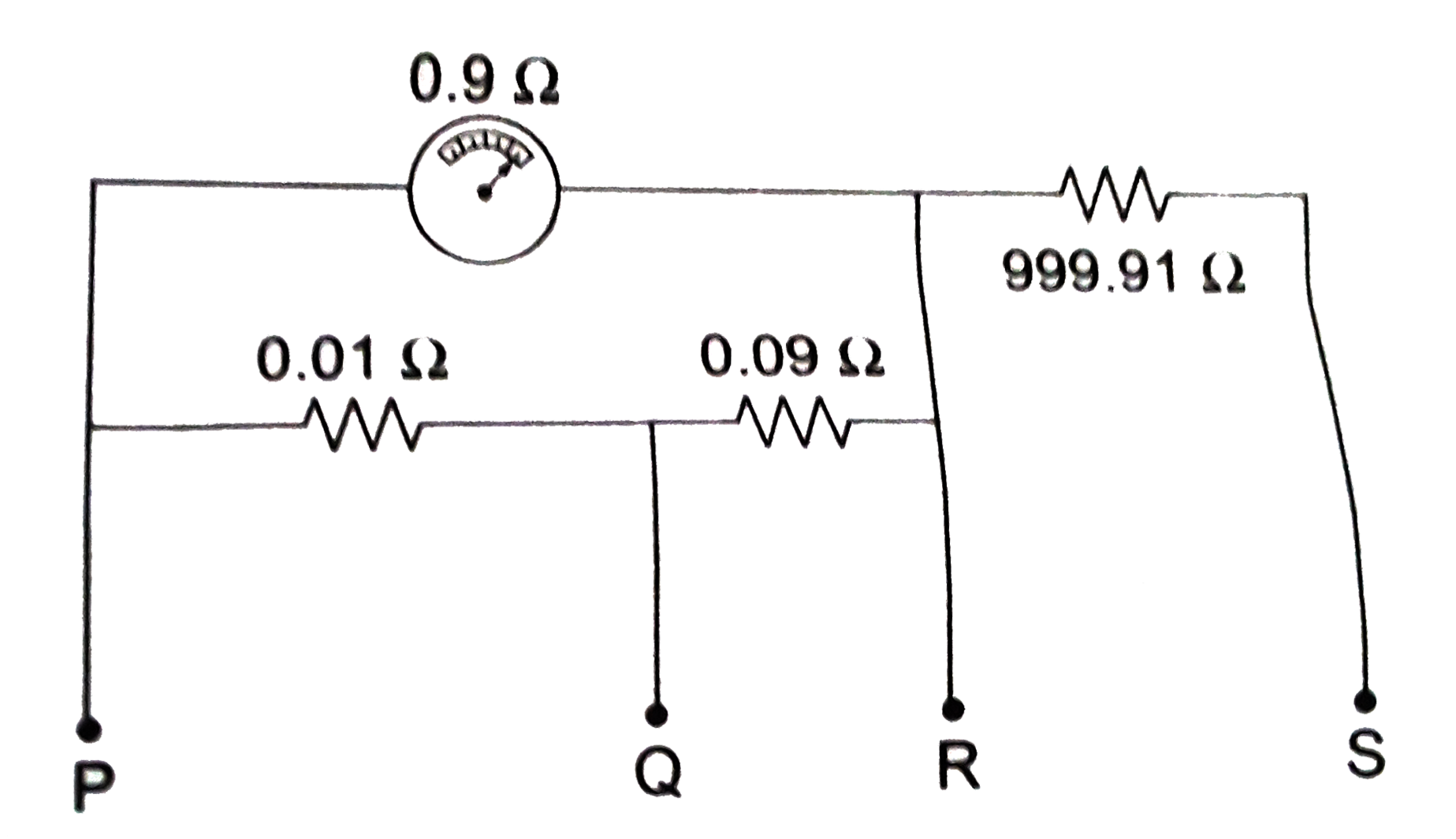
यदि मल्टीमीटर के टर्मिनल P तथा R से क्रमशः धारा का प्रवेश एंव निकास हो तब यह व्यवस्था एक ऐमीटर जैसा कार्य करेगी जिसका परास ( range ) हैं06:11View Solutionटेलीविजन , रेडियो जैसे इलेक्ट्रॉनिक साधनों के विद्युत - परिपथ की जाँच के क्रम में मल्टीमीटर का उपयोग किया जाता हैं । इस यंत्र में एक मिलीऐमीटर (milliameter) को विभिन्न प्रतिरोधों से जोड़कर विभिन्न परास (range) की धारा , विभवांतर तथा प्रतिरोधों का मापन किया जाता हैं । चित्र में मल्टीमीटर का परिपथ दिखाया गया हैं जिसके टर्मिनल P से धारा प्रवेश करती हैं और जो मिलीऐमीटर से तथा इसके श्रेणी तथा समांतरक्रम में जुड़े प्रतिरोधकों से प्रवाहित होकर अन्य किसी टर्मिनल Q , R ,S बाहर निकलती हैं । धारा को किस टर्मिनल से बाहर निकलना हैं यह इस बात पर निर्भर करता हैं कि मल्टीमीटर का उपयोग ऐमीटर , वोल्टमीटर या प्रतिरोध मापक के रुप में किस परास (range) के मापन के लिया किया जाना हैं । दिए गए चित्र में मिलीऐमीटर की कुंडली का प्रतिरोध `0.9 Omega ` तथा इससे 10 mA की धारा प्रवाहित होने पर यह पूर्ण स्केल विक्षेप ( full scale deflection ) देता हैं ।
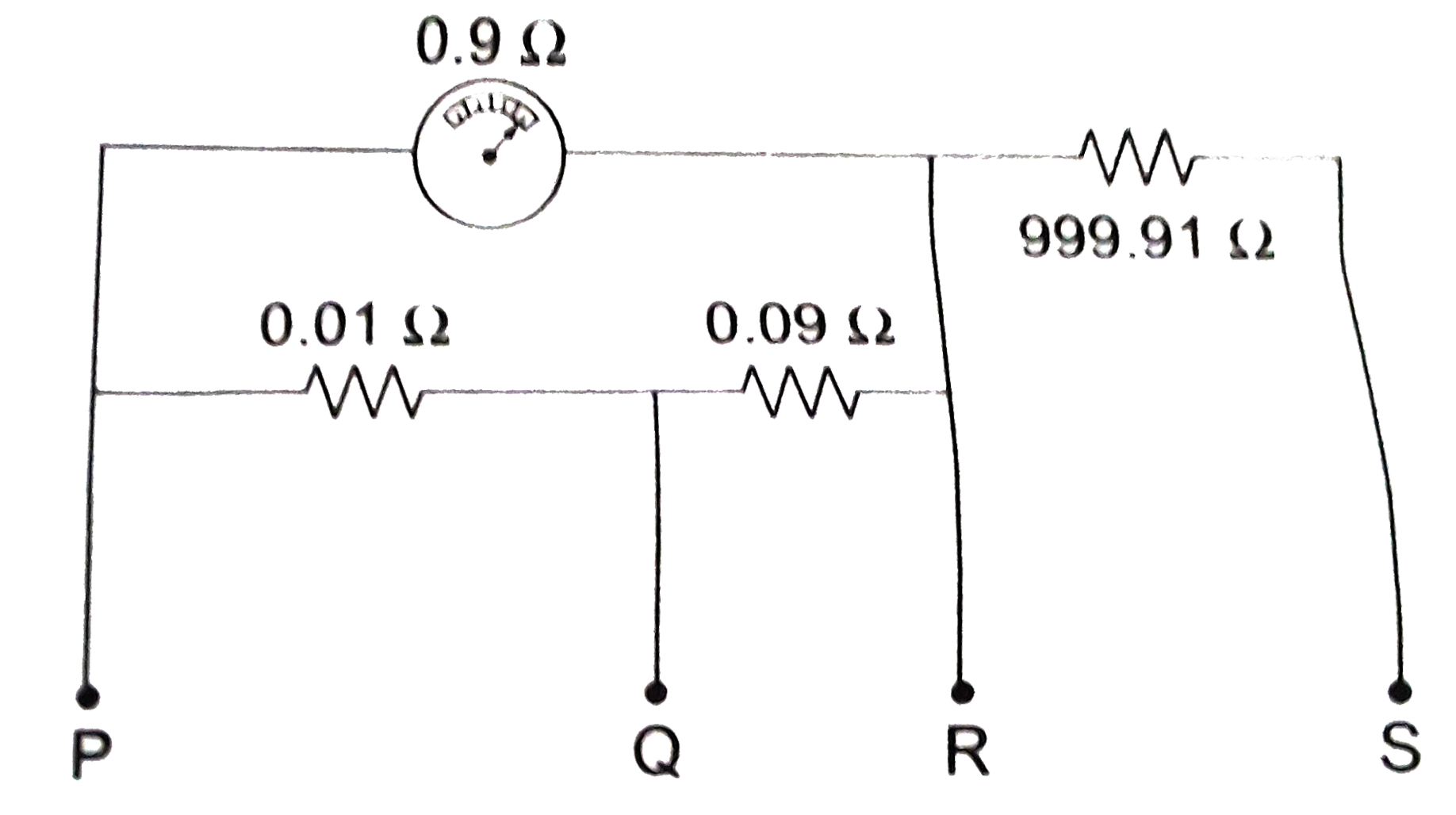
यदि मल्टीमीटर के टर्मिनल P से S से क्रमशः धारा का प्रवेश एंव निकास हो तब इस व्यवस्था व्दारा एक वोल्टमीटर जैसा उपयोग होगा जिसकी माप सीमा ( measuring range) होगी08:58View Solutionचित्र में विभवमापी का परिपथ प्रदर्शित हैं । विभवमापी के तार AB की लंबाई 50 cm हैं तथा दो सेल के विद्युत - वाहक बल क्रमशः `epsi_(1)` = 2V तथा `epsi_(2)` अज्ञात हैं । सेलों का आंतरिक प्रतिरोध नगण्य हैं । तथा `R_(1) = 15 Omega` और `R_(2) = 5 Omega` हैं । जब दोनों स्विच `k_(1)` तथा `k_(2)` खुले हों तब संतुलन बिंदु ( null point) की बिंदु A से दूरी 31.25 cm पर प्राप्त होती हैं । जब `k_(1)` तथा `k_(2)` दोनों बंद हो तब संतुलन बिंदु की A से दूरी घटकर मात्र 5 cm रह जाती हैं । तार AB का प्रतिरोध `10 Omega` मान लें ।
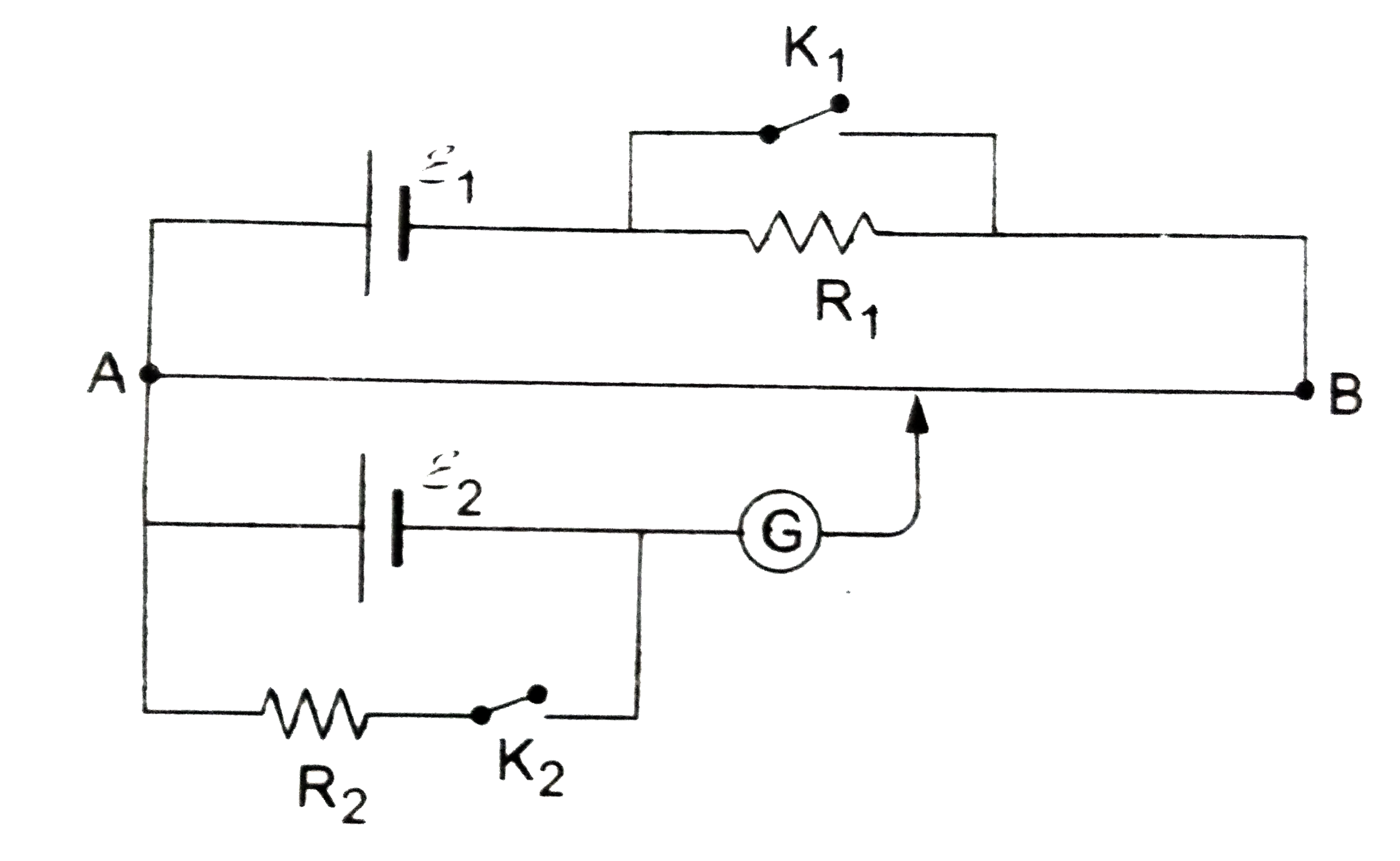
सेल `epsi_(2)` का विद्युत वाहक बल हैं06:15View Solutionचित्र में विभवमापी का परिपथ प्रदर्शित हैं । विभवमापी के तार AB की लंबाई 50 cm हैं तथा दो सेल के विद्युत - वाहक बल क्रमशः `epsi_(1)` = 2V तथा `epsi_(2)` अज्ञात हैं । सेलों का आंतरिक प्रतिरोध नगण्य हैं । तथा `R_(1) = 15 Omega` और `R_(2) = 5 Omega` हैं । जब दोनों स्विच `k_(1)` तथा `k_(2)` खुले हों तब संतुलन बिंदु ( null point) की बिंदु A से दूरी 31.25 cm पर प्राप्त होती हैं । जब `k_(1)` तथा `k_(2)` दोनों बंद हो तब संतुलन बिंदु की A से दूरी घटकर मात्र 5 cm रह जाती हैं । तार AB का प्रतिरोध `10 Omega` मान लें ।
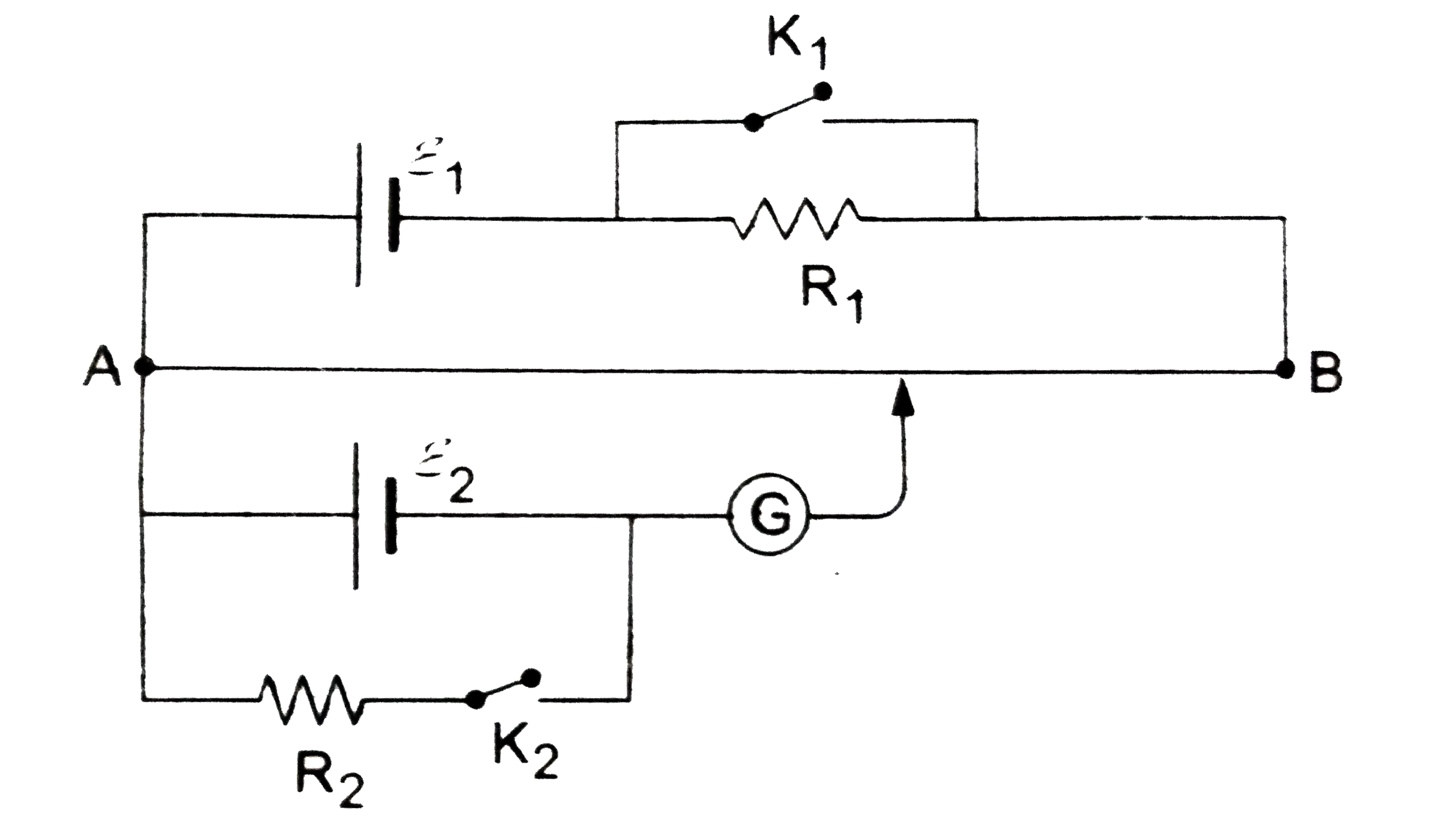
सेल `epsi_(2)` का आंतरिक प्रतिरोध हैं10:19View Solutionचित्र में विभवमापी का परिपथ प्रदर्शित हैं । विभवमापी के तार AB की लंबाई 50 cm हैं तथा दो सेल के विद्युत - वाहक बल क्रमशः `epsi_(1)` = 2V तथा `epsi_(2)` अज्ञात हैं । सेलों का आंतरिक प्रतिरोध नगण्य हैं । तथा `R_(1) = 15 Omega` और `R_(2) = 5 Omega` हैं । जब दोनों स्विच `k_(1)` तथा `k_(2)` खुले हों तब संतुलन बिंदु ( null point) की बिंदु A से दूरी 31.25 cm पर प्राप्त होती हैं । जब `k_(1)` तथा `k_(2)` दोनों बंद हो तब संतुलन बिंदु की A से दूरी घटकर मात्र 5 cm रह जाती हैं । तार AB का प्रतिरोध `10 Omega` मान लें ।
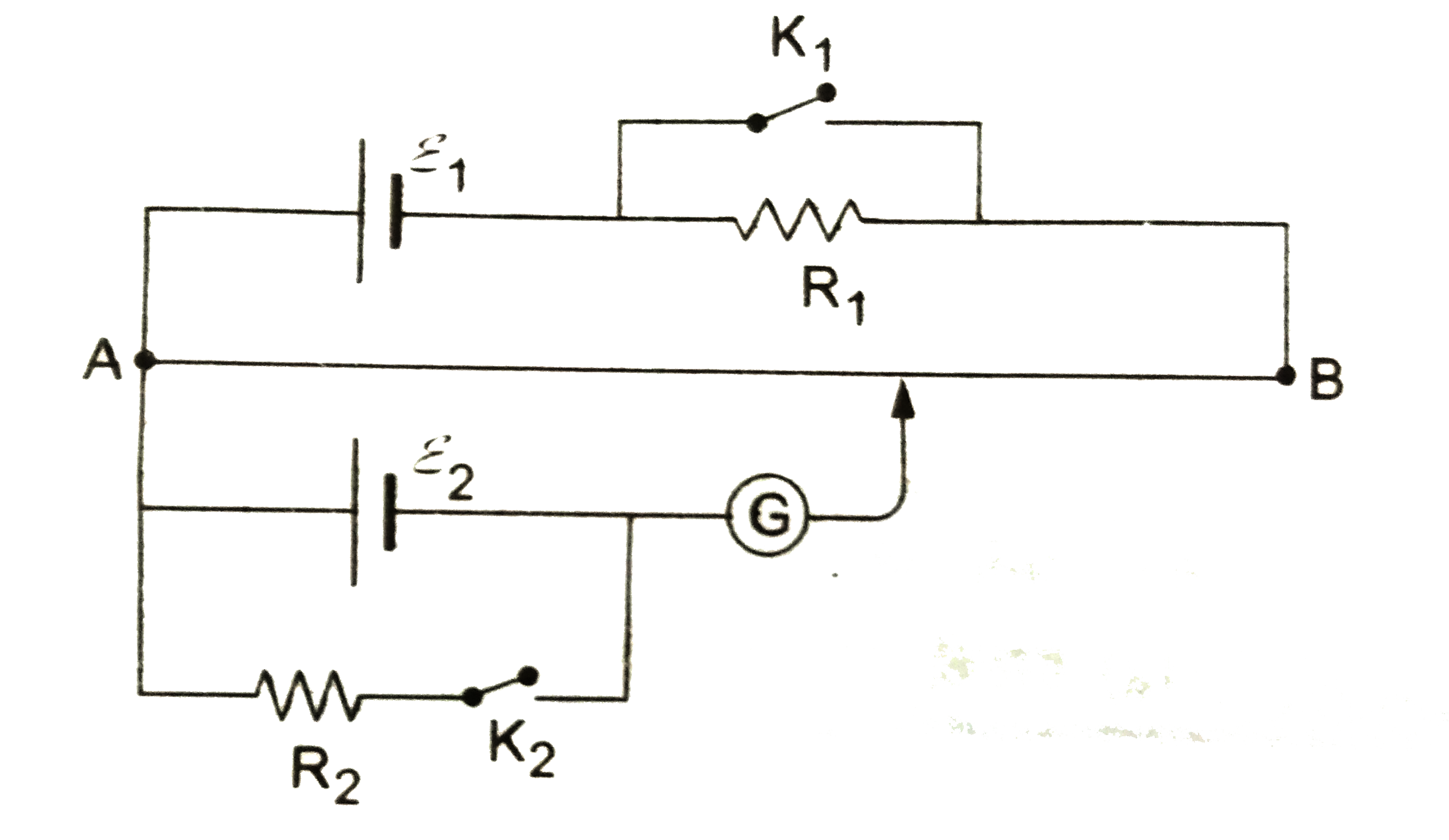
स्विच `K_(1)` को बंद तथा `K_(2)` को खुला रखने पर शून्य विक्षेप (null deflection) के संगत लंबाई हैं08:46View Solutionसमय के साथ परिवर्ती चुंबकीय क्षेत्र के कारण हमेशा विद्युत - क्षेत्र भी संबध्द रहता हैं । इसी संदर्भ में चित्र में प्रदर्शित R त्रिज्या के बेलनाकार क्षेत्र के अक्ष के अनुरेख चुंबकीय क्षेत्र `vec(B)` के समय के साथ परिवर्तन की दर `(dB)/(dt) = prop` टेसला प्रति सेकंड हैं ।
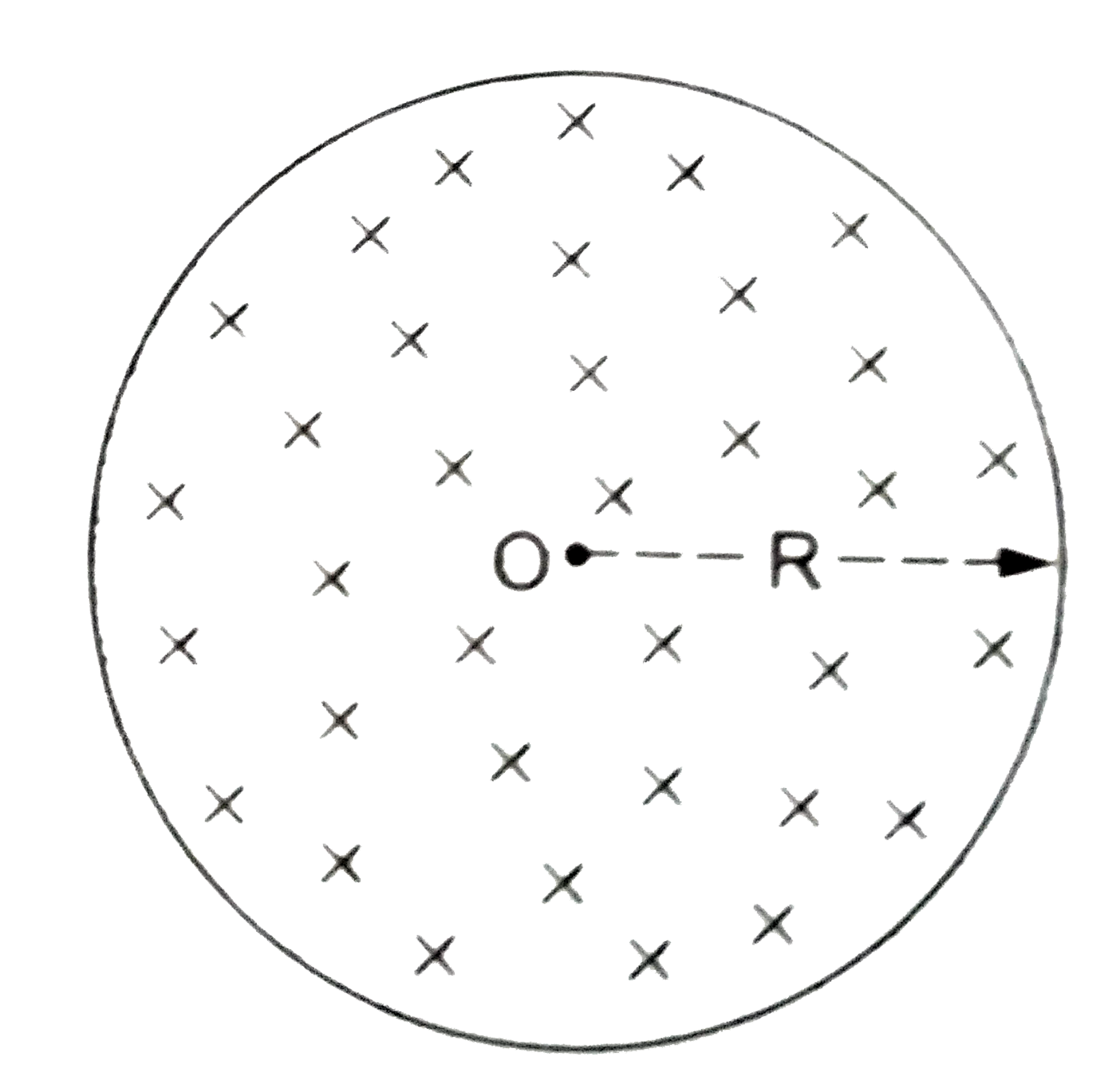
केंद्र O से r दूरी पर प्रेरित विद्युत - क्षेत्र का परिमाण यदि ` r lt R` हो04:34View Solutionसमय के साथ परिवर्ती चुंबकीय क्षेत्र के कारण हमेशा विद्युत - क्षेत्र भी संबध्द रहता हैं । इसी संदर्भ में चित्र में प्रदर्शित R त्रिज्या के बेलनाकार क्षेत्र के अक्ष के अनुरेख चुंबकीय क्षेत्र `vec(B)` के समय के साथ परिवर्तन की दर `(dB)/(dt) = prop` टेसला प्रति सेकंड हैं ।
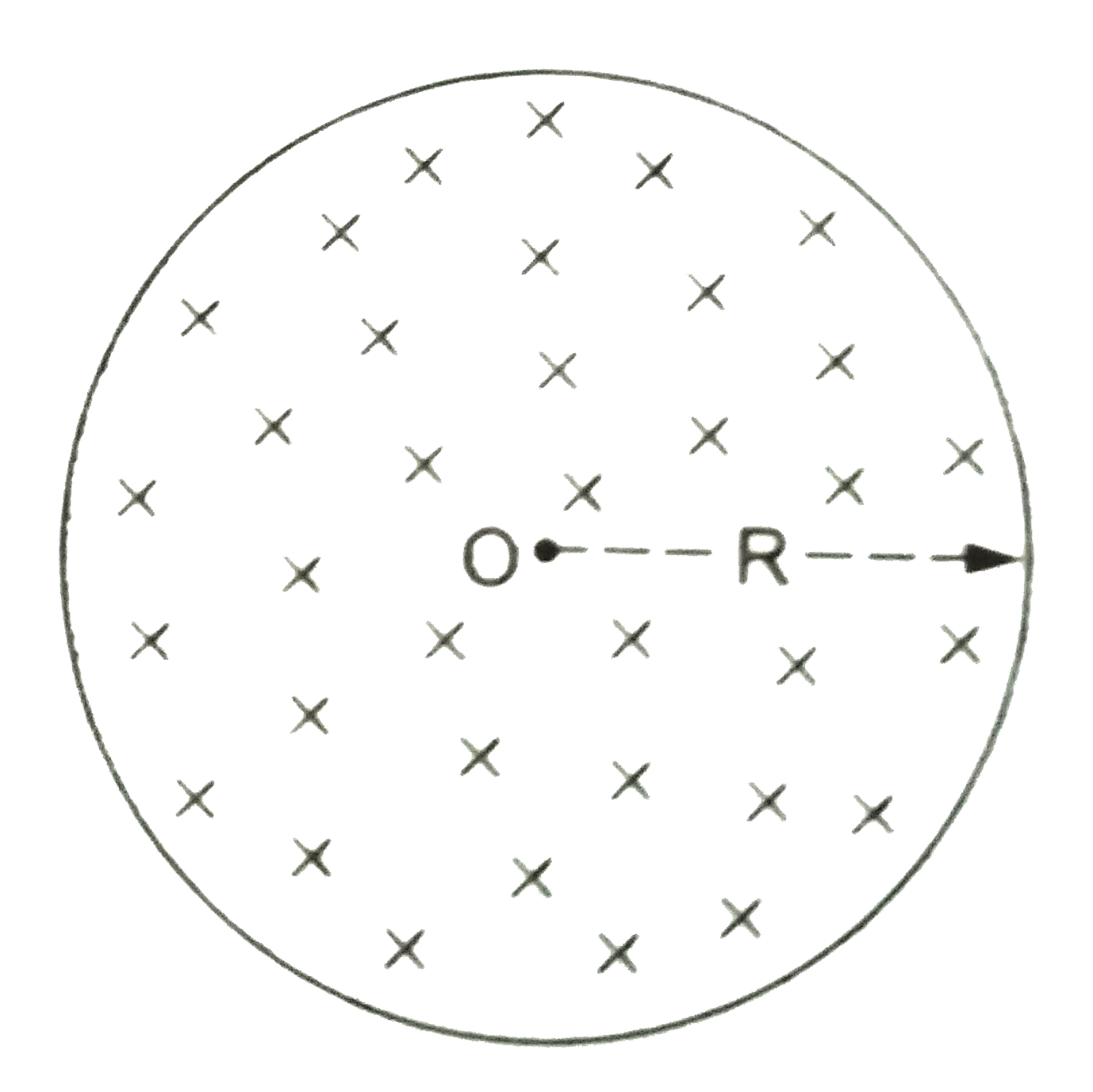
केंद्र O से r दूरी पर प्रेरित विद्युत - क्षेत्र का परिमाण यदि ` R lt r` हो04:34View Solutionसमय के साथ परिवर्ती चुंबकीय क्षेत्र के कारण हमेशा विद्युत - क्षेत्र भी संबध्द रहता हैं । इसी संदर्भ में चित्र में प्रदर्शित R त्रिज्या के बेलनाकार क्षेत्र के अक्ष के अनुरेख चुंबकीय क्षेत्र `vec(B)` के समय के साथ परिवर्तन की दर `(dB)/(dt) = prop` टेसला प्रति सेकंड हैं ।
आवेशित कण (द्रव्यमाण = m, आवेश = q) का तात्कालिक त्वरण जब वह केंद्र से r दूरी पर स्थित हो `(r gt R)`05:30View Solutionसमय के साथ परिवर्ती चुंबकीय क्षेत्र के कारण हमेशा विद्युत - क्षेत्र भी संबध्द रहता हैं । इसी संदर्भ में चित्र में प्रदर्शित R त्रिज्या के बेलनाकार क्षेत्र के अक्ष के अनुरेख चुंबकीय क्षेत्र `vec(B)` के समय के साथ परिवर्तन की दर `(dB)/(dt) = prop` टेसला प्रति सेकंड हैं ।
प्रेरित विद्युत - क्षेत्र E का केंद्र O से दूरी r के साथ विचरण किस ग्राफ व्दारा व्यक्त होता हैं ?02:39View Solutionइलेक्ट्रॉन के विशिष्ट आवेश ( specific charge ) , अर्थात् अनुपात , आवेश/द्रव्यमान `((e)/(m))` के निर्धारण के लिए सर जे0 जे0 थॉमसन व्दारा किए गए प्रयोग की व्यवस्था का आधुनिक प्रतिरुप चित्र में प्रदर्शित हैं । तप्त फिलामेंट F व्दारा उत्सर्जित इलेक्ट्रॉनों को विभवांतर V के अधीन त्वरित किया जाता हैं । सरल रेखा में गतिशील इलेक्ट्रॉनपुंज पर्दे C में बने संकीर्ण छिद्र से होकर बाहर निकलने के बाद एक ऐसे क्षेत्र से होकर गुजरता हैं जहाँ इलेक्ट्रॉन की संचरण दिशा के लंबवत परस्पर लंबवत दिशाओं में चुंबकीय क्षेत्र `vec(B)` तथा विद्युत क्षेत्र `vec(E)` दोनों वर्तमान हैं । इसके बाद इलेक्ट्रॉनपुंज बिना क्षेत्र वाले स्थान से होकर प्रतिदीप्ति परदे (fluorescent screen) S पर आघात कर दीप्ति उत्पन्न करता हैं । इलक्ट्रॉन के गमन वाला पूरा क्षेत्र निर्वातित ( evacuated) रहता हैं ।
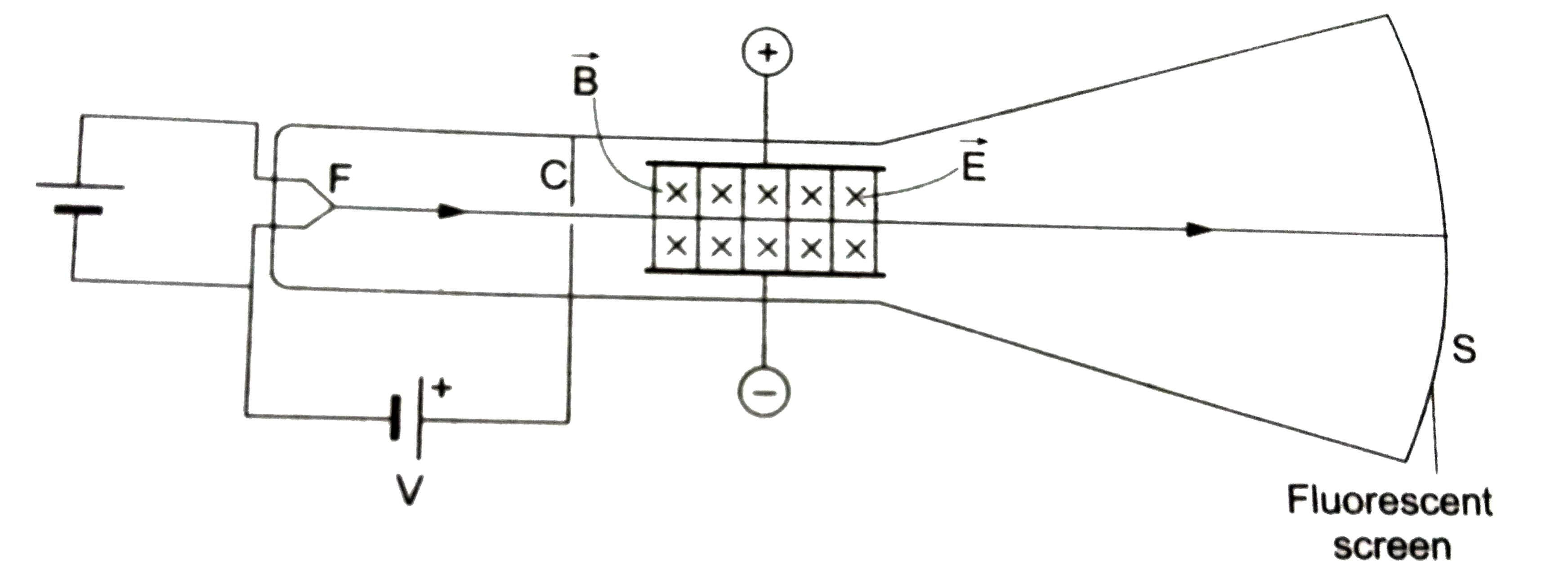
सर्वप्रथम `vec(E)` तथा `vec(B)` क्षेत्रों की अनुपस्थिति में पर्दे S पर अविक्षेपित (undeflected) इलेक्ट्रॉन व्दारा उत्पन्न प्रदीप्त - बिंदु की स्थिति नोट की जाती हैं । फिर , विद्युत - क्षेत्र `vec(E)` की उपस्थिति में इलेक्ट्रॉन - पुंज का पर्दे पर विक्षेप `d_(1)` नोट किया जाता हैं । इसके बाद चुंबकीय क्षेत्र `vec(B)` की प्रबलता को समंजित कर दीप्ति - बिंदु को पुनः प्रारंभिक अविक्षेपित स्थिति में लाया जाता हैं । इस अवस्था में विद्युतीय बल `F_(e)` तथा चुंबकीय बल `F_(B)` एक - दूसरे को निष्फल कर देते हैं , अर्थात् `e_(E) = ev_(B)`. प्राप्त प्रेक्षणों से इलेक्ट्रॉन का विशिष्ट द्रव्यमान `(e)/(m)` निर्धारित किया जाता हैं ।
थॉमसन की प्रायोगिक व्यवस्था में टयूब को निर्वातित करने की आवश्यकता क्यो हुई ? थॉमसन की प्रायोगिक व्यवस्था में टयूब को निर्वातित करने की आवश्यकता क्यों हुई ?05:57View Solutionइलेक्ट्रॉन के विशिष्ट आवेश ( specific charge ) , अर्थात् अनुपात , आवेश/द्रव्यमान `((e)/(m))` के निर्धारण के लिए सर जे0 जे0 थॉमसन व्दारा किए गए प्रयोग की व्यवस्था का आधुनिक प्रतिरुप चित्र में प्रदर्शित हैं । तप्त फिलामेंट F व्दारा उत्सर्जित इलेक्ट्रॉनों को विभवांतर V के अधीन त्वरित किया जाता हैं । सरल रेखा में गतिशील इलेक्ट्रॉनपुंज पर्दे C में बने संकीर्ण छिद्र से होकर बाहर निकलने के बाद एक ऐसे क्षेत्र से होकर गुजरता हैं जहाँ इलेक्ट्रॉन की संचरण दिशा के लंबवत परस्पर लंबवत दिशाओं में चुंबकीय क्षेत्र `vec(B)` तथा विद्युत क्षेत्र `vec(E)` दोनों वर्तमान हैं । इसके बाद इलेक्ट्रॉनपुंज बिना क्षेत्र वाले स्थान से होकर प्रतिदीप्ति परदे (fluorescent screen) S पर आघात कर दीप्ति उत्पन्न करता हैं । इलक्ट्रॉन के गमन वाला पूरा क्षेत्र निर्वातित ( evacuated) रहता हैं ।
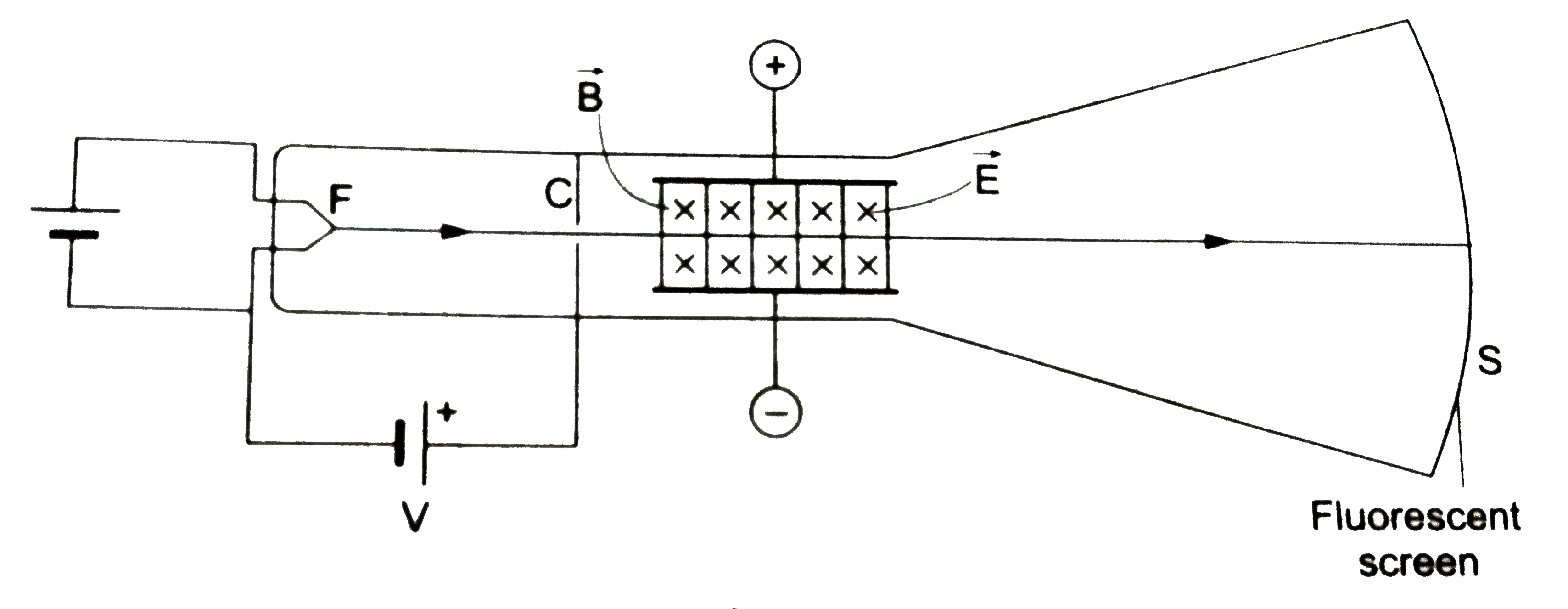
सर्वप्रथम `vec(E)` तथा `vec(B)` क्षेत्रों की अनुपस्थिति में पर्दे S पर अविक्षेपित (undeflected) इलेक्ट्रॉन व्दारा उत्पन्न प्रदीप्त - बिंदु की स्थिति नोट की जाती हैं । फिर , विद्युत - क्षेत्र `vec(E)` की उपस्थिति में इलेक्ट्रॉन - पुंज का पर्दे पर विक्षेप `d_(1)` नोट किया जाता हैं । इसके बाद चुंबकीय क्षेत्र `vec(B)` की प्रबलता को समंजित कर दीप्ति - बिंदु को पुनः प्रारंभिक अविक्षेपित स्थिति में लाया जाता हैं । इस अवस्था में विद्युतीय बल `F_(e)` तथा चुंबकीय बल `F_(B)` एक - दूसरे को निष्फल कर देते हैं , अर्थात् `e_(E) = ev_(B)`. प्राप्त प्रेक्षणों से इलेक्ट्रॉन का विशिष्ट द्रव्यमान `(e)/(m)` निर्धारित किया जाता हैं ।
यदि त्वरक विभवातंर (accelerating potential) V का मान बढ़ाकर इलेक्ट्रॉन की चाल दुगुनी कर दी जाए तब `(e)/(m)` के सही निर्धारण के लिए निम्नलिखित कथनों में कौन कथन सही होगा ?05:22View Solutionइलेक्ट्रॉन के विशिष्ट आवेश ( specific charge ) , अर्थात् अनुपात , आवेश/द्रव्यमान `((e)/(m))` के निर्धारण के लिए सर जे0 जे0 थॉमसन व्दारा किए गए प्रयोग की व्यवस्था का आधुनिक प्रतिरुप चित्र में प्रदर्शित हैं । तप्त फिलामेंट F व्दारा उत्सर्जित इलेक्ट्रॉनों को विभवांतर V के अधीन त्वरित किया जाता हैं । सरल रेखा में गतिशील इलेक्ट्रॉनपुंज पर्दे C में बने संकीर्ण छिद्र से होकर बाहर निकलने के बाद एक ऐसे क्षेत्र से होकर गुजरता हैं जहाँ इलेक्ट्रॉन की संचरण दिशा के लंबवत परस्पर लंबवत दिशाओं में चुंबकीय क्षेत्र `vec(B)` तथा विद्युत क्षेत्र `vec(E)` दोनों वर्तमान हैं । इसके बाद इलेक्ट्रॉनपुंज बिना क्षेत्र वाले स्थान से होकर प्रतिदीप्ति परदे (fluorescent screen) S पर आघात कर दीप्ति उत्पन्न करता हैं । इलक्ट्रॉन के गमन वाला पूरा क्षेत्र निर्वातित ( evacuated) रहता हैं ।
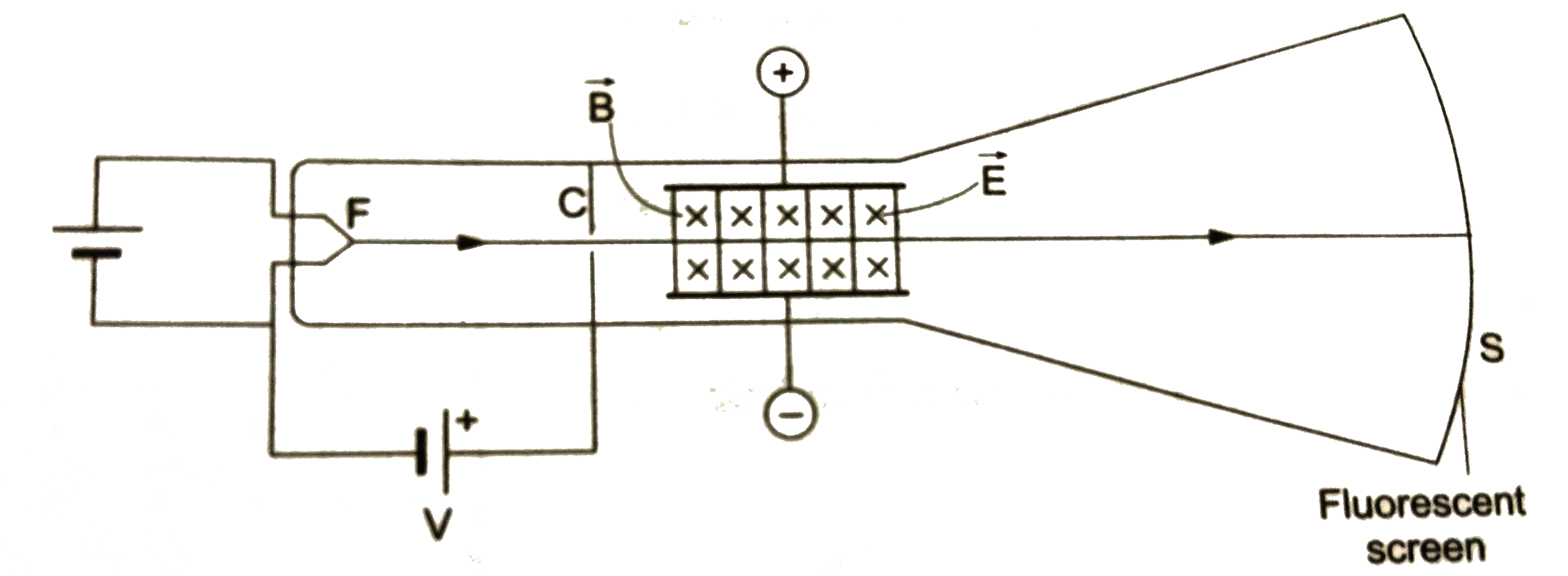
सर्वप्रथम `vec(E)` तथा `vec(B)` क्षेत्रों की अनुपस्थिति में पर्दे S पर अविक्षेपित (undeflected) इलेक्ट्रॉन व्दारा उत्पन्न प्रदीप्त - बिंदु की स्थिति नोट की जाती हैं । फिर , विद्युत - क्षेत्र `vec(E)` की उपस्थिति में इलेक्ट्रॉन - पुंज का पर्दे पर विक्षेप `d_(1)` नोट किया जाता हैं । इसके बाद चुंबकीय क्षेत्र `vec(B)` की प्रबलता को समंजित कर दीप्ति - बिंदु को पुनः प्रारंभिक अविक्षेपित स्थिति में लाया जाता हैं । इस अवस्था में विद्युतीय बल `F_(e)` तथा चुंबकीय बल `F_(B)` एक - दूसरे को निष्फल कर देते हैं , अर्थात् `e_(E) = ev_(B)`. प्राप्त प्रेक्षणों से इलेक्ट्रॉन का विशिष्ट द्रव्यमान `(e)/(m)` निर्धारित किया जाता हैं ।
चित्र में प्रदर्शित व्यवस्था में केवल विद्युत क्षेत्र की उपस्थिति में इलेक्ट्रॉन - पुंज का विक्षेप ऊपर की ओर होता हैं । विक्षेप को शून्य करने के लिए विद्युत - क्षेत्र E तथा चुंबकीय क्षेत्र B की दिशाएँ क्या होंगी ?08:00View Solutionएक चुंबकीय क्षेत्र `vec(B) = ((B_(0)y)/(a))hatk` कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । `B_(0)` तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
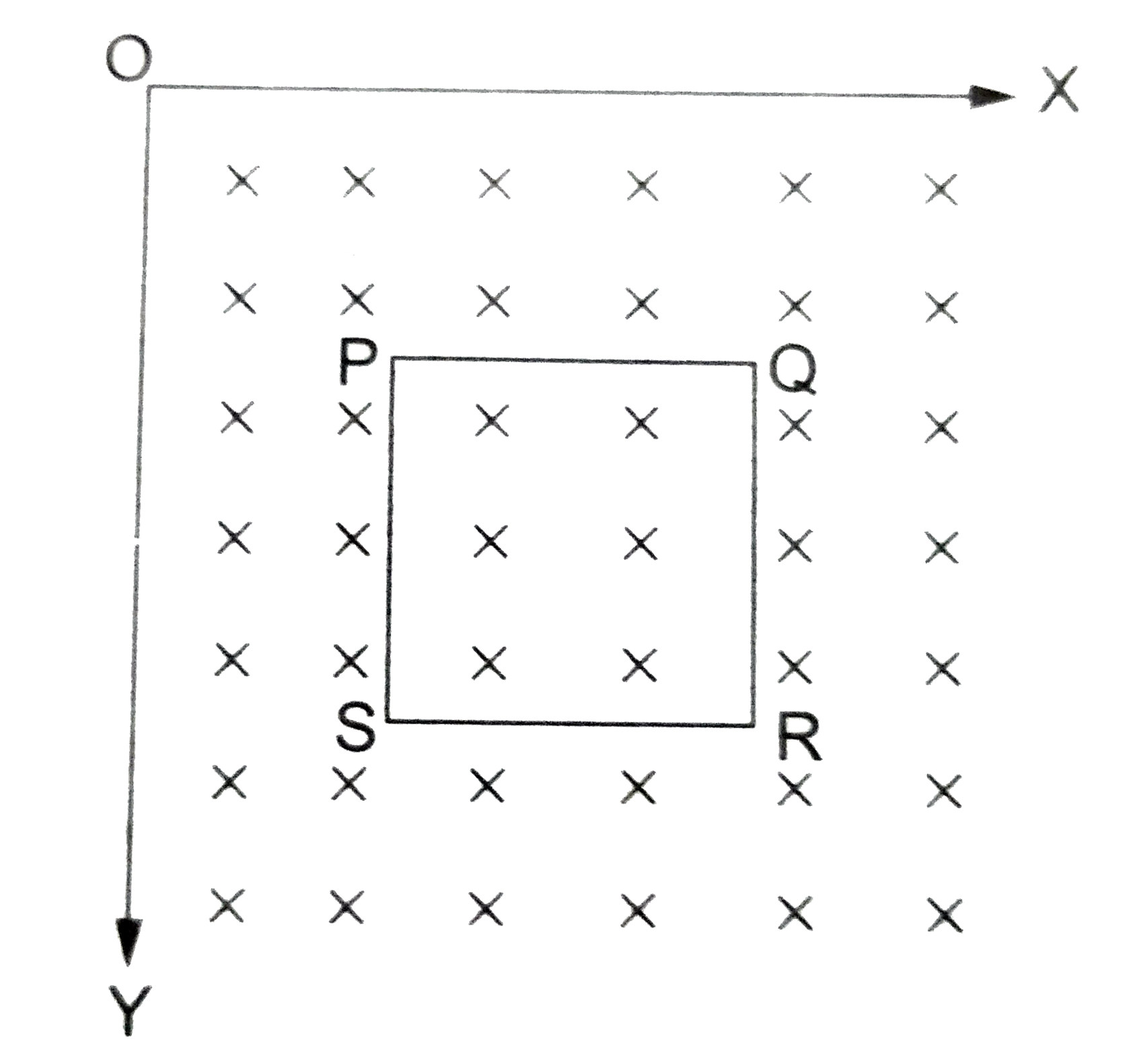
गति के क्रम में जब लूप की चाल v हो तब लूप में प्रेरित धारा का मान तथा दिशा हैं08:05View Solutionएक चुंबकीय क्षेत्र `vec(B) = ((B_(0)y)/(a))hatk` कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । `B_(0)` तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
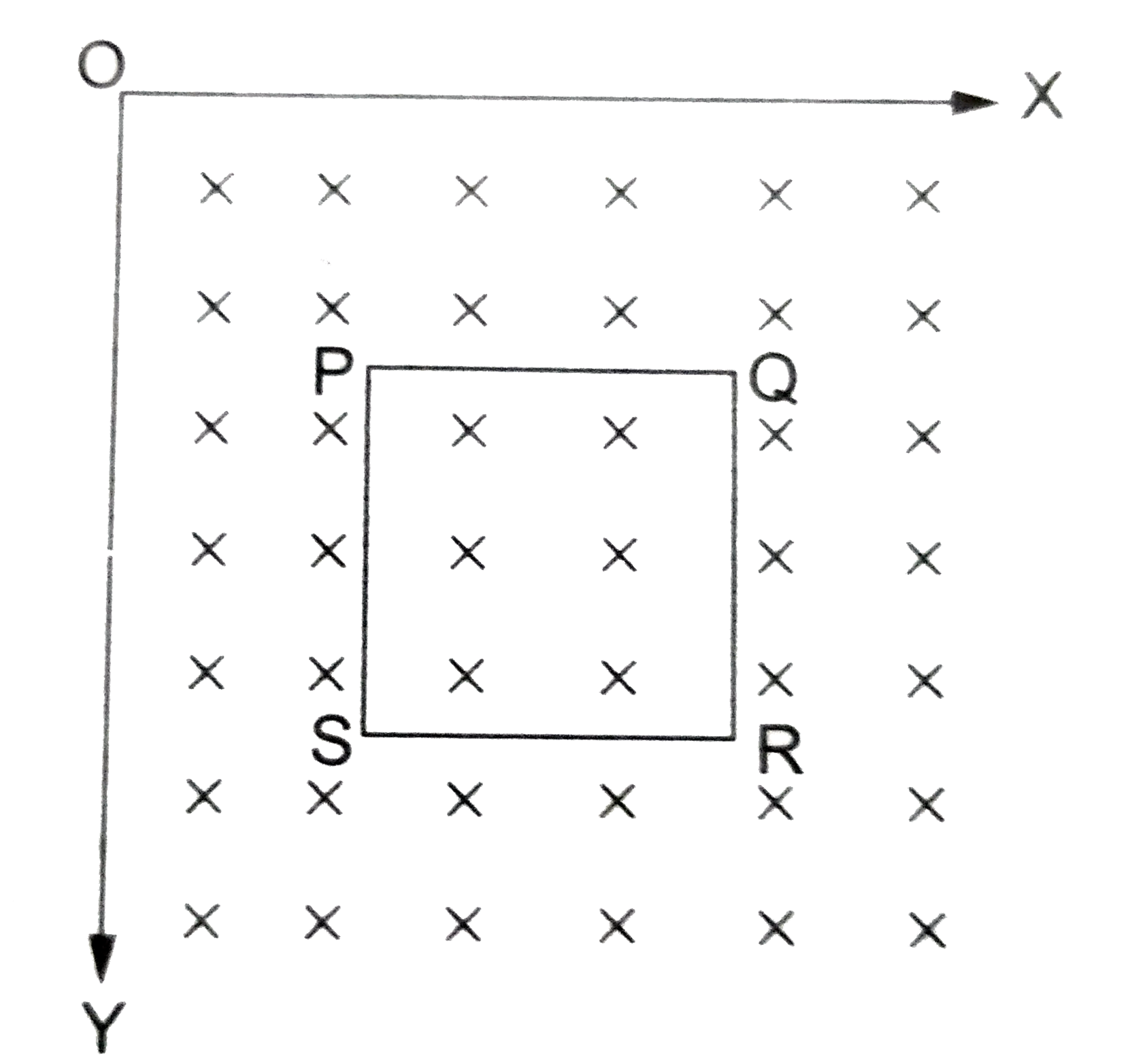
गति के क्रम में जब लूप की चाल v हो तब लूप पर आरोपित नेट लोरेंट्ज़ बल का परिमाण एवं दिशा है15:45View Solutionएक चुंबकीय क्षेत्र `vec(B) = ((B_(0)y)/(a))hatk` कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । `B_(0)` तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
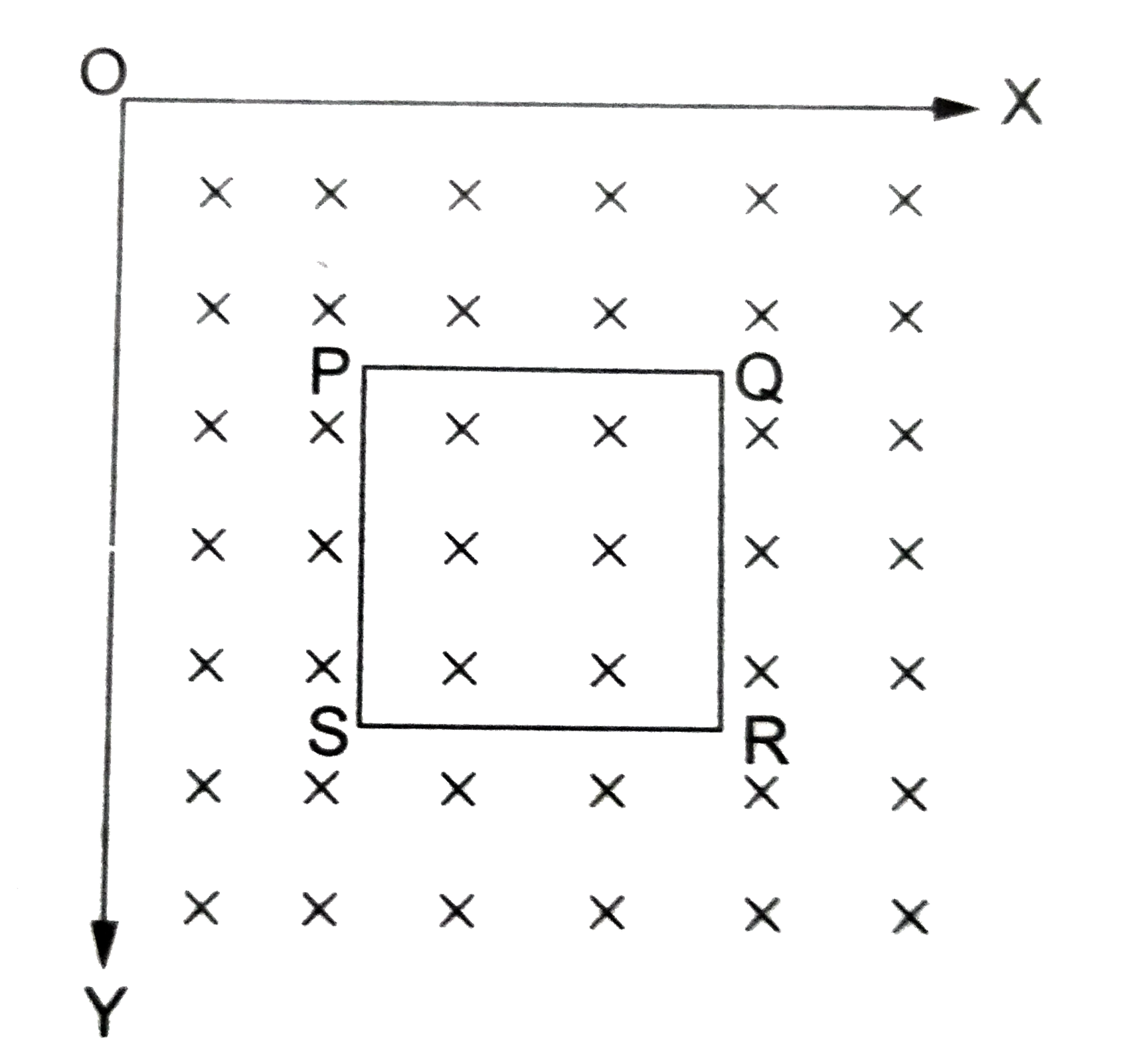
गुरुत्व की अनुपस्थिति में यदि लूप एकसमान वेग v से xy-तल में x-अक्ष के समांतर गतिशील हो तब लूप में प्रेरित धारा का मान तथा दिशा हैं04:54View Solutionप्रत्यावर्ती धारा परिपथ (a.c. circuit ) में शक्ति - गुणांक ( power factor ) एक महत्त्वपूर्ण पैरामीटर (parameter) है जिसके व्दारा परिपथ के प्रतिरोधी (resistive ) होने की कोटि (degree) का ज्ञान होता हैं । यह परिपथ के प्रतिरोध R तथा प्रतिबाधा ( impedance) Z के अनुपात से परिभाषित होता हैं । यह मूलतः परिपथ की वोल्टता ( voltage) एंव धारा के बीच (phase differennce ) की कोज्या (cosine ) के तुल्य हैं ।
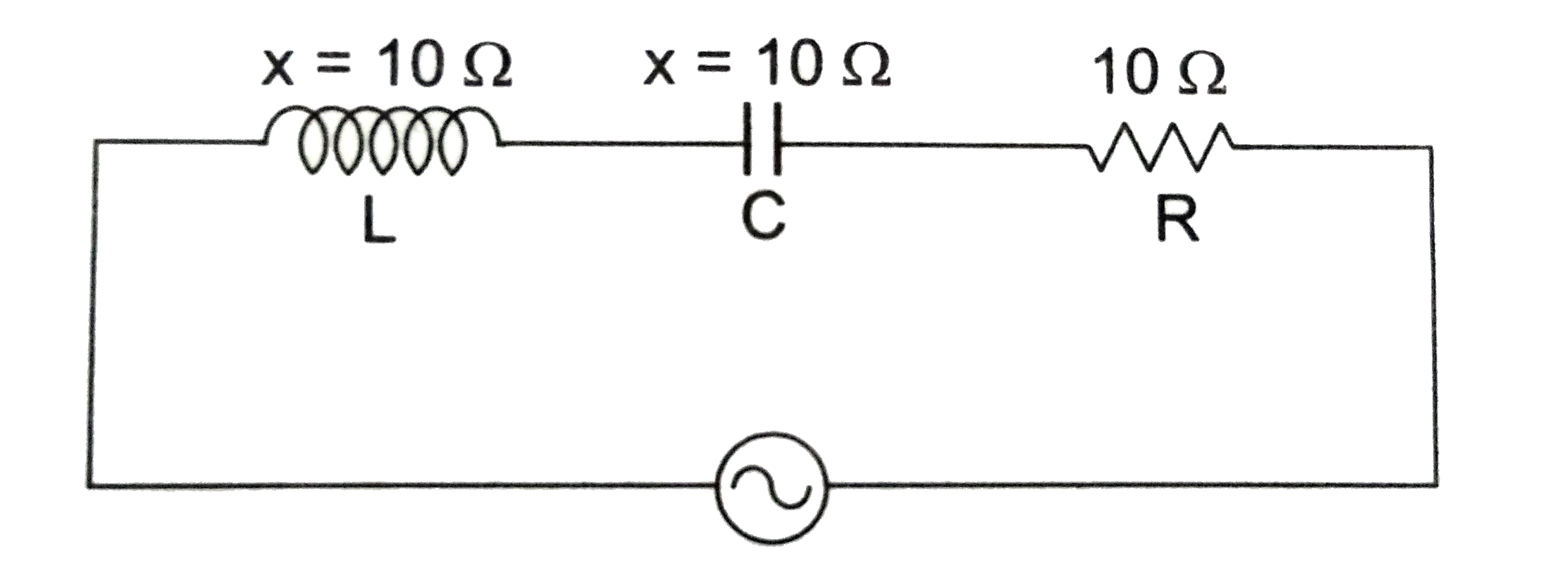
श्रेणीबध्द L - C - R युग्म का शक्ति - गुणांक हैं
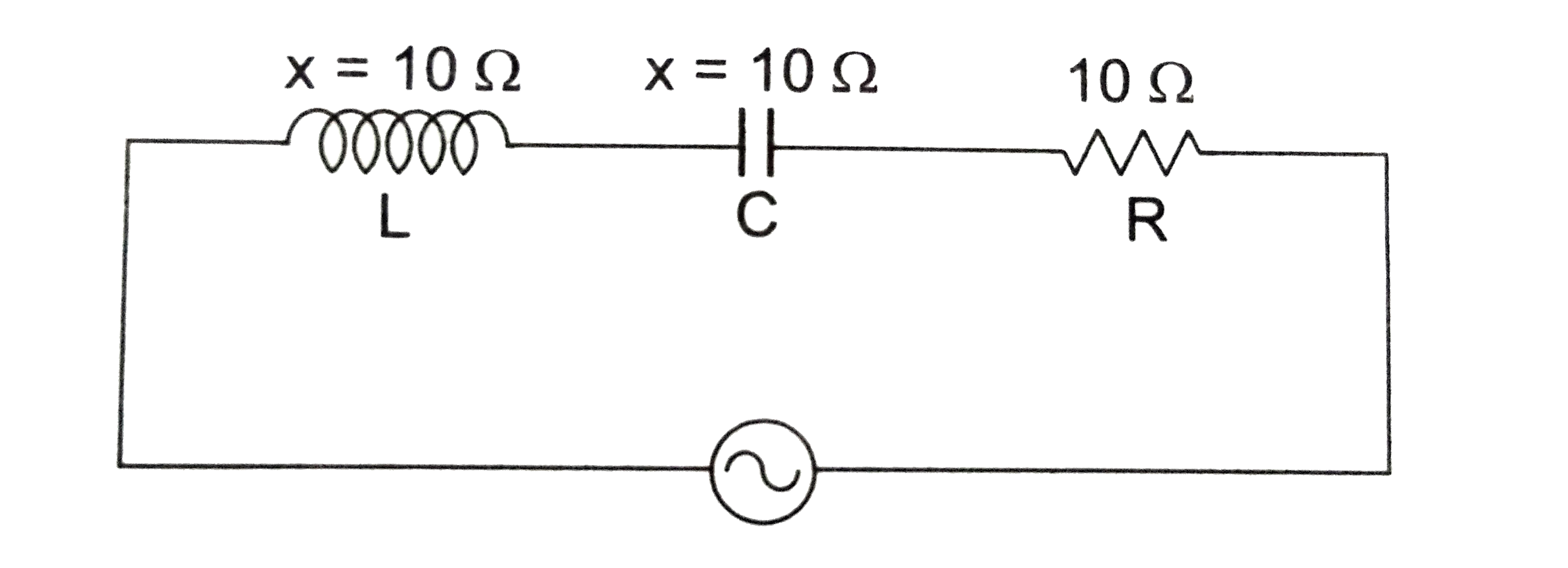 02:30View Solution
02:30View Solutionप्रत्यावर्ती धारा परिपथ (a.c. circuit ) में शक्ति - गुणांक ( power factor ) एक महत्त्वपूर्ण पैरामीटर (parameter) है जिसके व्दारा परिपथ के प्रतिरोधी (resistive ) होने की कोटि (degree) का ज्ञान होता हैं । यह परिपथ के प्रतिरोध R तथा प्रतिबाधा ( impedance) Z के अनुपात से परिभाषित होता हैं । यह मूलतः परिपथ की वोल्टता ( voltage) एंव धारा के बीच (phase differennce ) की कोज्या (cosine ) के तुल्य हैं ।
यदि प्रत्यावर्ती धारा ( a,c.) स्रोत की आवृति बढाई जाए तो परिपथ का शक्ति गुणांक03:02View Solutionप्रत्यावर्ती धारा परिपथ (a.c. circuit ) में शक्ति - गुणांक ( power factor ) एक महत्त्वपूर्ण पैरामीटर (parameter) है जिसके व्दारा परिपथ के प्रतिरोधी (resistive ) होने की कोटि (degree) का ज्ञान होता हैं । यह परिपथ के प्रतिरोध R तथा प्रतिबाधा ( impedance) Z के अनुपात से परिभाषित होता हैं । यह मूलतः परिपथ की वोल्टता ( voltage) एंव धारा के बीच (phase differennce ) की कोज्या (cosine ) के तुल्य हैं ।
घूर्णी - सदिश ( rotating vector) व्दारा व्यक्त फेजर आरेख के लिए शक्ति - गुणांक का मान हैं
 07:22View Solution
07:22View Solutionकिसी आवेशित संधारित्र को एक प्रेरित्र के साथ जोड़कर अनावेशन क्रिया (discharging process) के क्रम में विद्युतीय दोलन होता हैं । इस प्रक्रम में संधारित्र की विद्युत - ऊर्जा एंव प्रेरित्र की चुंबकीय ऊर्जा के बीच परस्पर विनिमय (exchange) होता हैं । दोलन का एक चक्र पूरा होने में लगा समय , अर्थात आवर्तकाल T का मान L तथा C पर निर्भर करता हैं जिसके लिए संबंध ` T = 2 pi sqrt(LC)` मान्य होता हैं । चित्र में आवेशित संधारित्र के लिए विभवातंर `V_(0)` है तथा स्विच S को समय t = 0 पर बंद किया जाता हैं |
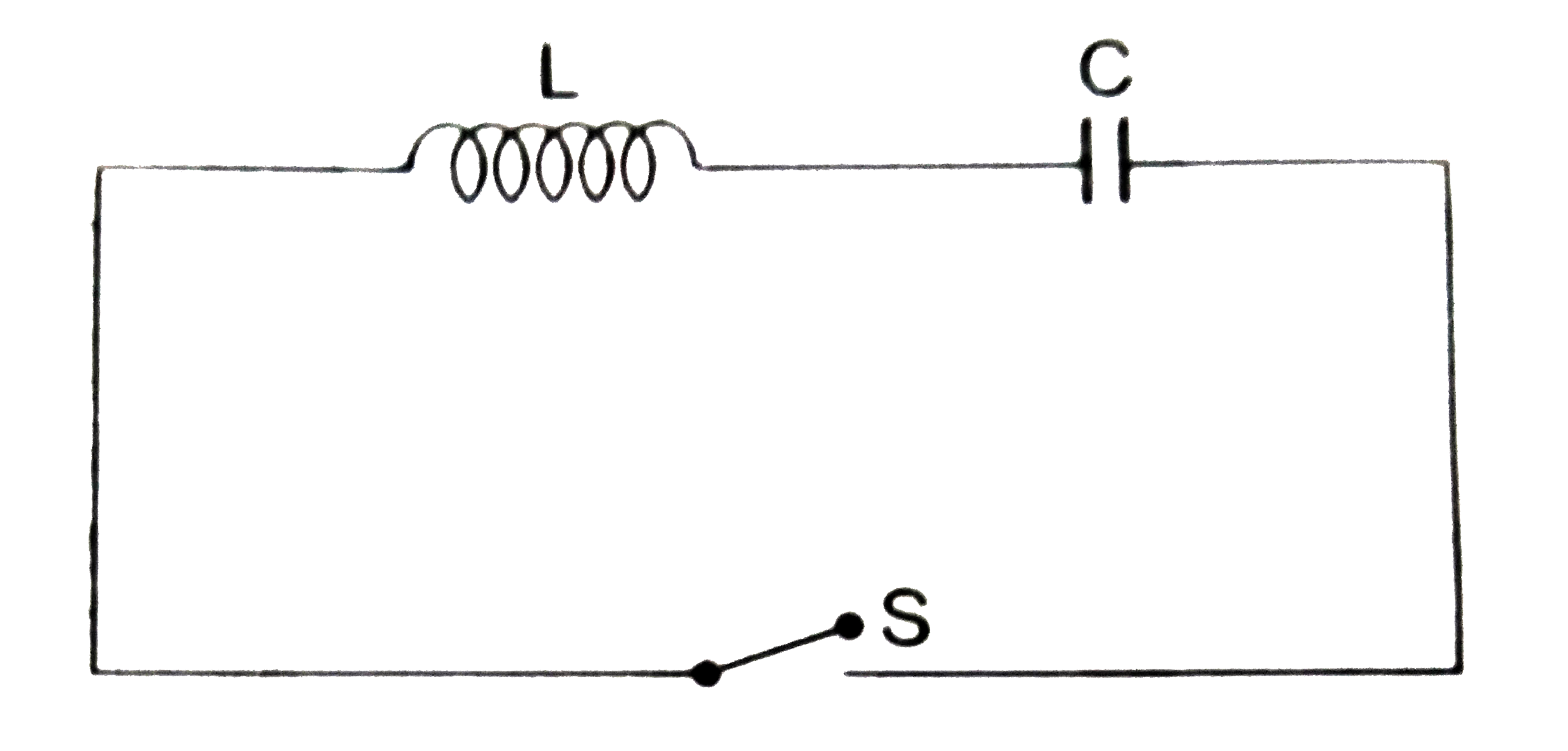
परिपथ में धारा का महत्तम मान हैं03:24View Solutionकिसी आवेशित संधारित्र को एक प्रेरित्र के साथ जोड़कर अनावेशन क्रिया (discharging process) के क्रम में विद्युतीय दोलन होता हैं । इस प्रक्रम में संधारित्र की विद्युत - ऊर्जा एंव प्रेरित्र की चुंबकीय ऊर्जा के बीच परस्पर विनिमय (exchange) होता हैं । दोलन का एक चक्र पूरा होने में लगा समय , अर्थात आवर्तकाल T का मान L तथा C पर निर्भर करता हैं जिसके लिए संबंध ` T = 2 pi sqrt(LC)` मान्य होता हैं । चित्र में आवेशित संधारित्र के लिए विभवातंर `V_(0)` है तथा स्विच S को समय t = 0 पर बंद किया जाता हैं |
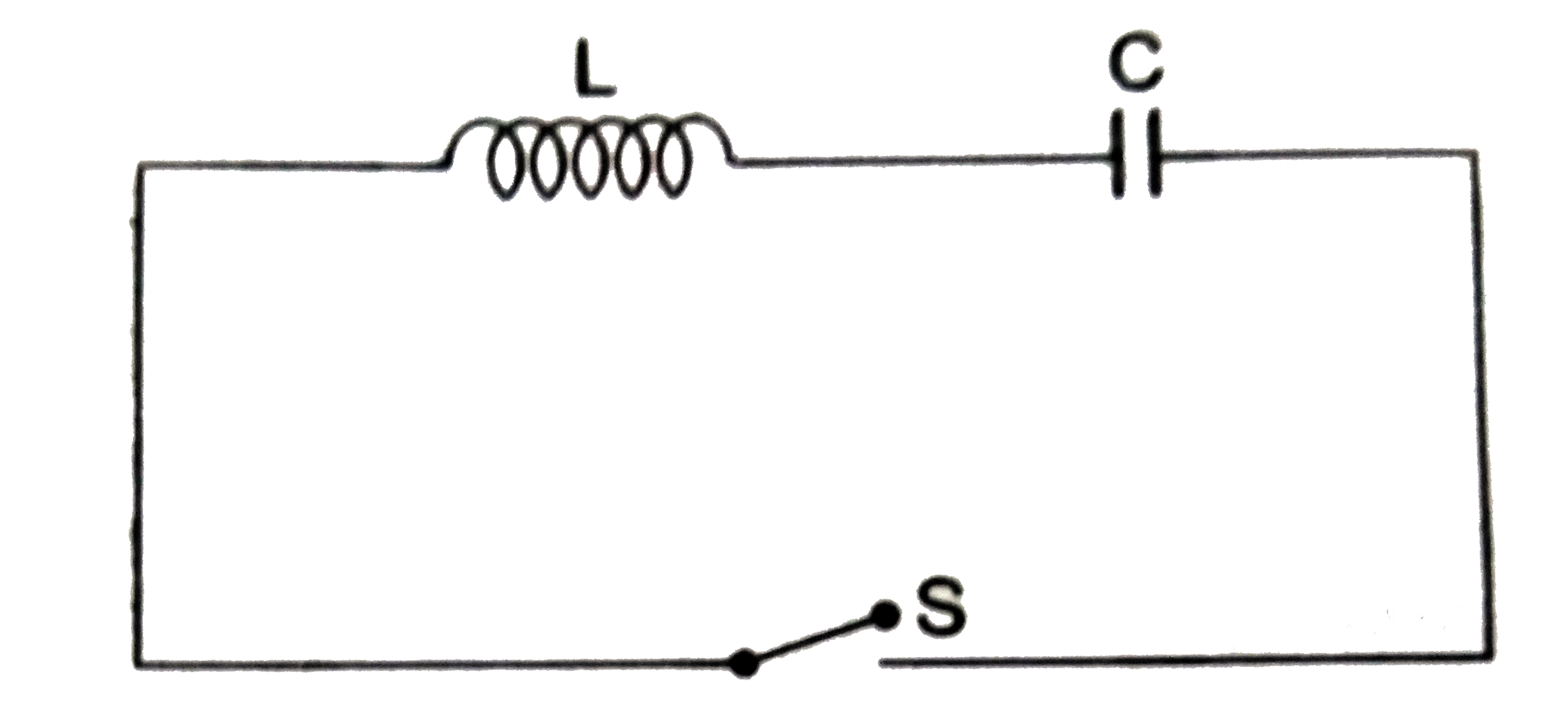
प्रेरित्र (inductor) में संचित चुंबकीय ऊर्जा का महत्तम मान हैं03:12View Solutionकिसी आवेशित संधारित्र को एक प्रेरित्र के साथ जोड़कर अनावेशन क्रिया (discharging process) के क्रम में विद्युतीय दोलन होता हैं । इस प्रक्रम में संधारित्र की विद्युत - ऊर्जा एंव प्रेरित्र की चुंबकीय ऊर्जा के बीच परस्पर विनिमय (exchange) होता हैं । दोलन का एक चक्र पूरा होने में लगा समय , अर्थात आवर्तकाल T का मान L तथा C पर निर्भर करता हैं जिसके लिए संबंध ` T = 2 pi sqrt(LC)` मान्य होता हैं । चित्र में आवेशित संधारित्र के लिए विभवातंर `V_(0)` है तथा स्विच S को समय t = 0 पर बंद किया जाता हैं |
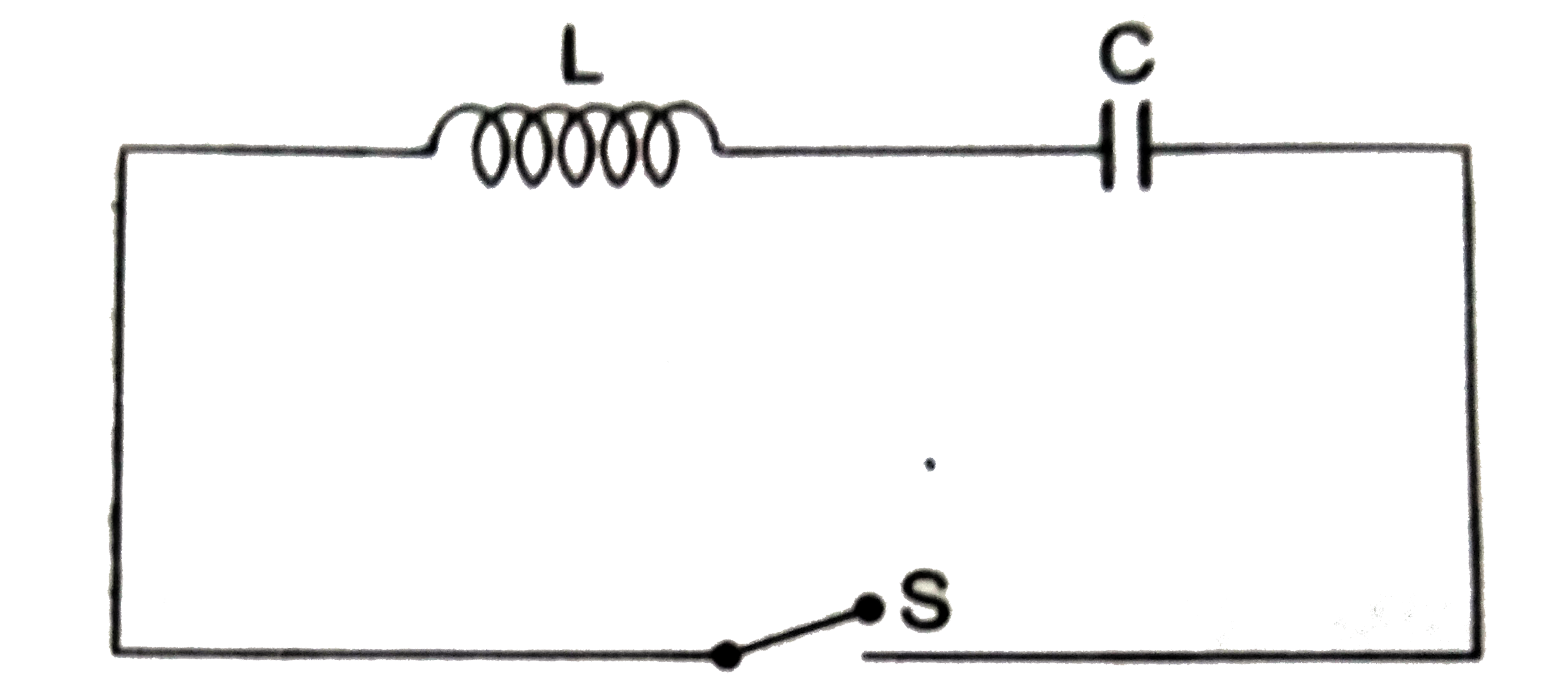
स्विच S को बंद करने के बाद संधारित्र पर सर्वप्रथम विभवांतर शून्य होने का समय हैं03:56View Solutionप्रत्यावर्ती धारा परिपथ में चुंबकीय क्षेत्र के माध्यम से विद्युत - ऊर्जा को एक परिपथ से दूसरे परिपथ में स्थानांतरित करने के लिए ट्रांसफॉर्मर प्रयुक्त किया जाता हैं जिसमें प्राथमिक (primary) तथा व्दितीयक (secondary ) कुंडलियाँ परतदार क्रोड पर लपेटी रहती हैं । प्राथमिक परिपथ में प्रत्यावर्ती धारा (a.c.) वोल्टता के एक स्त्रोत से प्राप्त विद्युत - ऊर्जा व्दितीयक में लगे बल्ब आदि को प्रदान की जाती हैं । इस प्रक्रिया में प्राथमिक एंव व्दितीयक परिपथ में वोल्टता `(V_(p) , V_(s))` तथा धारा `(I_(p) , I_(s))` के मान उनमें फेरों की संख्या `(N_(P) , N_(S))` पर निर्भर होते हैं । ट्रांसफार्मर के अध्ययन के क्रम में अग्रलिखित आँकड़े (data) प्राप्त किए गए ।

किसी ट्रांसफॉर्मर की प्राथमिक कुंडली में फेरों की संख्या 100 हैं तथा इसमें निवेशी प्रत्यावर्ती धारा वोल्टता (input a.c. volatage) 220 V हैं । व्दितीयक परिपथ में 4400 V की वोल्टता प्राप्त करने के लिए इसमें फेरों की संख्या क्या होगी ?03:17View Solutionप्रत्यावर्ती धारा परिपथ में चुंबकीय क्षेत्र के माध्यम से विद्युत - ऊर्जा को एक परिपथ से दूसरे परिपथ में स्थानांतरित करने के लिए ट्रांसफॉर्मर प्रयुक्त किया जाता हैं जिसमें प्राथमिक (primary) तथा व्दितीयक (secondary ) कुंडलियाँ परतदार क्रोड पर लपेटी रहती हैं । प्राथमिक परिपथ में प्रत्यावर्ती धारा (a.c.) वोल्टता के एक स्त्रोत से प्राप्त विद्युत - ऊर्जा व्दितीयक में लगे बल्ब आदि को प्रदान की जाती हैं । इस प्रक्रिया में प्राथमिक एंव व्दितीयक परिपथ में वोल्टता `(V_(p) , V_(s))` तथा धारा `(I_(p) , I_(s))` के मान उनमें फेरों की संख्या `(N_(P) , N_(S))` पर निर्भर होते हैं । ट्रांसफार्मर के अध्ययन के क्रम में अग्रलिखित आँकड़े (data) प्राप्त किए गए ।

120 V की वोल्टता के प्रत्यावर्ती धारा (a.c) स्त्रोत को किसी ट्रांसफॉर्मर के 40 फेरो वाली प्राथमिक कुंडली से जोड़ा गया हैं । यदि प्राथमिक कुंडली में 140 W की शक्ति का निवेश किया जाए तो व्दितीयक कुंडली में कितनी शक्ति प्राप्त होगी ?05:54View Solutionप्रत्यावर्ती धारा परिपथ में चुंबकीय क्षेत्र के माध्यम से विद्युत - ऊर्जा को एक परिपथ से दूसरे परिपथ में स्थानांतरित करने के लिए ट्रांसफॉर्मर प्रयुक्त किया जाता हैं जिसमें प्राथमिक (primary) तथा व्दितीयक (secondary ) कुंडलियाँ परतदार क्रोड पर लपेटी रहती हैं । प्राथमिक परिपथ में प्रत्यावर्ती धारा (a.c.) वोल्टता के एक स्त्रोत से प्राप्त विद्युत - ऊर्जा व्दितीयक में लगे बल्ब आदि को प्रदान की जाती हैं । इस प्रक्रिया में प्राथमिक एंव व्दितीयक परिपथ में वोल्टता `(V_(p) , V_(s))` तथा धारा `(I_(p) , I_(s))` के मान उनमें फेरों की संख्या `(N_(P) , N_(S))` पर निर्भर होते हैं । ट्रांसफार्मर के अध्ययन के क्रम में अग्रलिखित आँकड़े (data) प्राप्त किए गए ।

किसी ट्रांसफॉर्मर की प्राथमिक कुंडली में 200 फेरे हैं तथा इसमें15 V की बैटरी जोड़कर 2.0 mA की धारा प्रवाहित की जाती हैं । यदि व्दितीयक कुंडली के फेरों की संख्या 100 हो तो इसमें कितनी धारा प्रवाहित होगी ?03:15View Solutionनाभिक की संरचना प्रोटॉन तथा न्यूट्रॉन के कारण होती हैं , जहाँ प्रोटॉन धनावेशित कण हैं जबकि न्यूट्रॉन अनावेशित होता हैं । न्यूट्रॉन के क्वार्क मॉडल ( quark model ) के आधार पर इसका नेट आवेश शून्य रहने पर भी इसे अशून्य (nonzero) चुबंकीय आघूर्ण प्राप्त हैं जिसका z-घटक `9.66 xx 10^(-27) A - m^(2)` होता हैं । इस संकल्पना की व्याख्या न्यूट्रॉन के आंतरिक बनावट के आधार पर की जा सकती हैं । न्यूट्रॉन की सरंचना तीन प्रकार के मौलिक कणों ( fundamental particles) व्दारा होती हैं जिन्हें क्वार्क (quark) कहा जाता हैंः
एक अप क्वार्क ( up quark ) , संकेत u , आवेश + `(2e)/(3)`
दो डाउन क्वार्क ( down quark ) , संकेत d , प्रत्येक पर आवेश - `(e)/(3)`
तीन प्रकार के कणों के सम्मिलित प्रभाव से न्यूट्रॉन का नेट आवेश = `(2e)/(3) - (e)/(3) - (e)/(3) ` = शून्य । यदि ये क्वार्क गतिमान हो तब इनके व्दारा उत्पन्न चुंबकीय आघूर्ण अशून्य हो सकता हैं । चित्र में प्रदर्शित सरल मॉडल में u - क्वार्क r त्रिज्या v से वामावर्त दिशा में (anticlockwise) घूम रहा हैं तथा दोनों d - क्वार्क उसी वृतीय पथ पर समान वेग v से दक्षिणावर्त दिशा में (clockwise) घूम रहे हैं ।
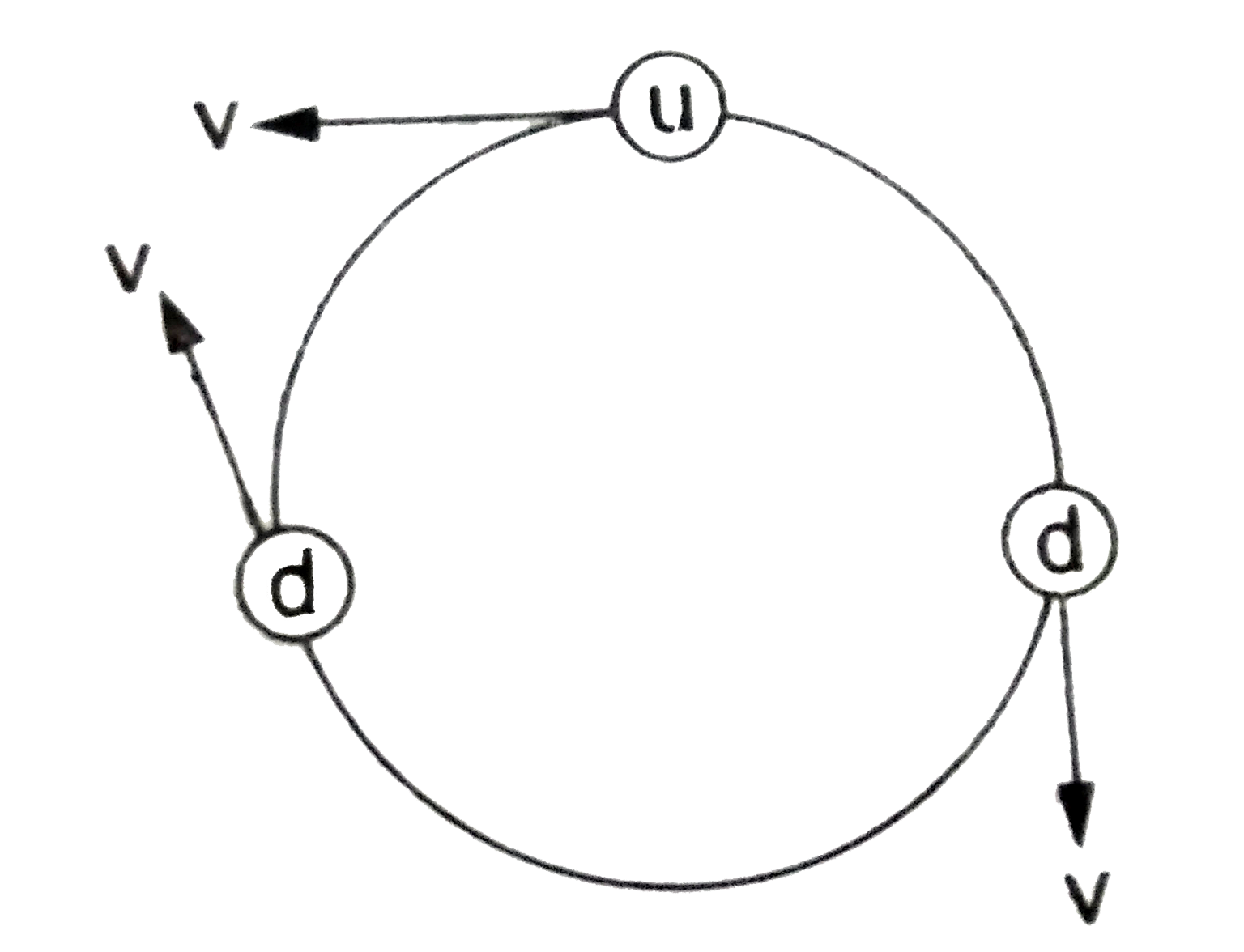
u - क्वार्क की एकसमान वृत्तीय गति के कारण तुल्य विद्युत - धारा हैं03:51View Solutionनाभिक की संरचना प्रोटॉन तथा न्यूट्रॉन के कारण होती हैं , जहाँ प्रोटॉन धनावेशित कण हैं जबकि न्यूट्रॉन अनावेशित होता हैं । न्यूट्रॉन के क्वार्क मॉडल ( quark model ) के आधार पर इसका नेट आवेश शून्य रहने पर भी इसे अशून्य (nonzero) चुबंकीय आघूर्ण प्राप्त हैं जिसका z-घटक `9.66 xx 10^(-27) A - m^(2)` होता हैं । इस संकल्पना की व्याख्या न्यूट्रॉन के आंतरिक बनावट के आधार पर की जा सकती हैं । न्यूट्रॉन की सरंचना तीन प्रकार के मौलिक कणों ( fundamental particles) व्दारा होती हैं जिन्हें क्वार्क (quark) कहा जाता हैंः
एक अप क्वार्क ( up quark ) , संकेत u , आवेश + `(2e)/(3)`
दो डाउन क्वार्क ( down quark ) , संकेत d , प्रत्येक पर आवेश - `(e)/(3)`
तीन प्रकार के कणों के सम्मिलित प्रभाव से न्यूट्रॉन का नेट आवेश = `(2e)/(3) - (e)/(3) - (e)/(3) ` = शून्य । यदि ये क्वार्क गतिमान हो तब इनके व्दारा उत्पन्न चुंबकीय आघूर्ण अशून्य हो सकता हैं । चित्र में प्रदर्शित सरल मॉडल में u - क्वार्क r त्रिज्या v से वामावर्त दिशा में (anticlockwise) घूम रहा हैं तथा दोनों d - क्वार्क उसी वृतीय पथ पर समान वेग v से दक्षिणावर्त दिशा में (clockwise) घूम रहे हैं ।
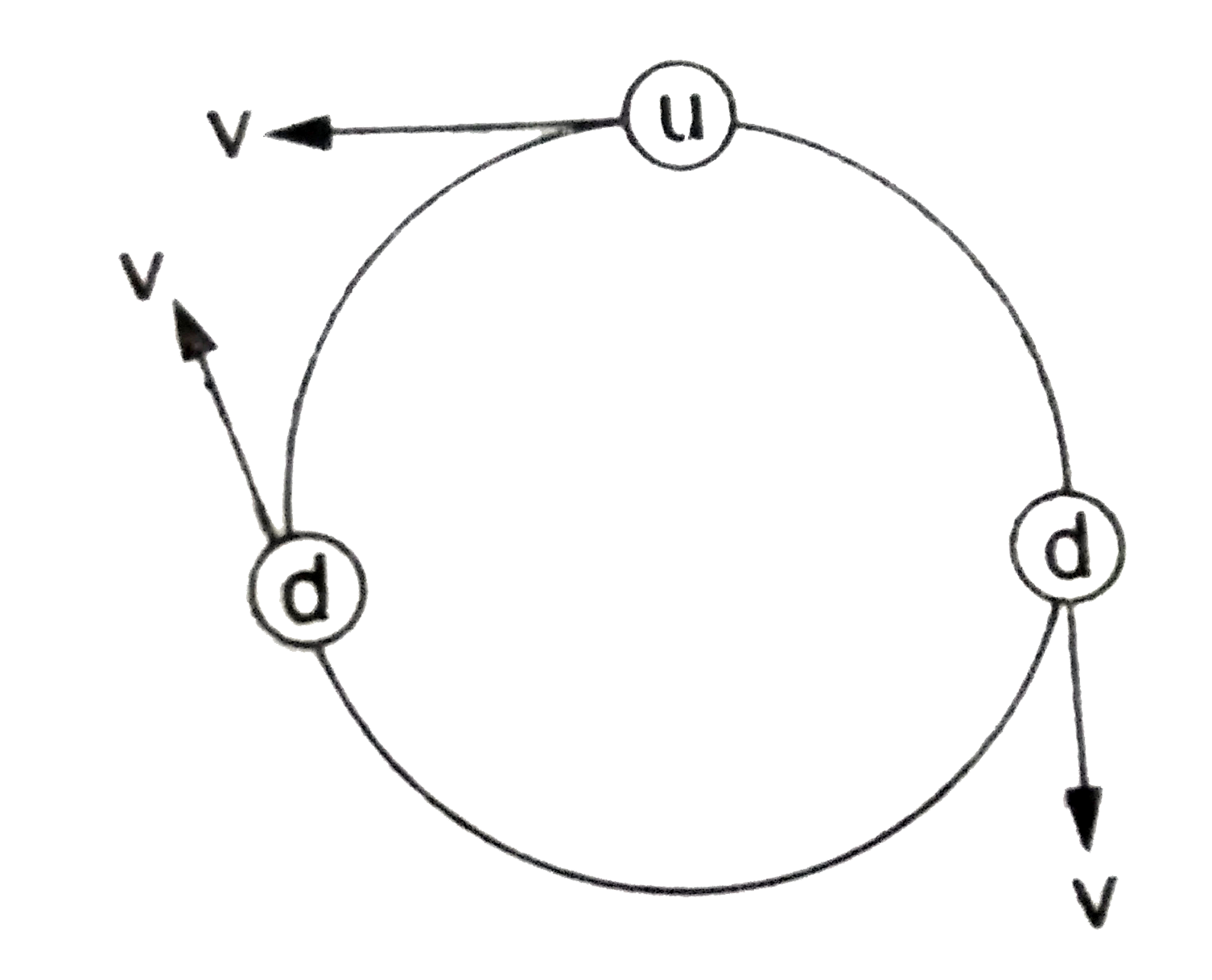
तीनों क्वार्क के निकाय के सम्मिलित प्रभाव के कारण नेट चुंबकीय आपूर्ण का परिणाम03:53View Solutionनाभिक की संरचना प्रोटॉन तथा न्यूट्रॉन के कारण होती हैं , जहाँ प्रोटॉन धनावेशित कण हैं जबकि न्यूट्रॉन अनावेशित होता हैं । न्यूट्रॉन के क्वार्क मॉडल ( quark model ) के आधार पर इसका नेट आवेश शून्य रहने पर भी इसे अशून्य (nonzero) चुबंकीय आघूर्ण प्राप्त हैं जिसका z-घटक `9.66 xx 10^(-27) A - m^(2)` होता हैं । इस संकल्पना की व्याख्या न्यूट्रॉन के आंतरिक बनावट के आधार पर की जा सकती हैं । न्यूट्रॉन की सरंचना तीन प्रकार के मौलिक कणों ( fundamental particles) व्दारा होती हैं जिन्हें क्वार्क (quark) कहा जाता हैंः
एक अप क्वार्क ( up quark ) , संकेत u , आवेश + `(2e)/(3)`
दो डाउन क्वार्क ( down quark ) , संकेत d , प्रत्येक पर आवेश - `(e)/(3)`
तीन प्रकार के कणों के सम्मिलित प्रभाव से न्यूट्रॉन का नेट आवेश = `(2e)/(3) - (e)/(3) - (e)/(3) ` = शून्य । यदि ये क्वार्क गतिमान हो तब इनके व्दारा उत्पन्न चुंबकीय आघूर्ण अशून्य हो सकता हैं । चित्र में प्रदर्शित सरल मॉडल में u - क्वार्क r त्रिज्या v से वामावर्त दिशा में (anticlockwise) घूम रहा हैं तथा दोनों d - क्वार्क उसी वृतीय पथ पर समान वेग v से दक्षिणावर्त दिशा में (clockwise) घूम रहे हैं ।
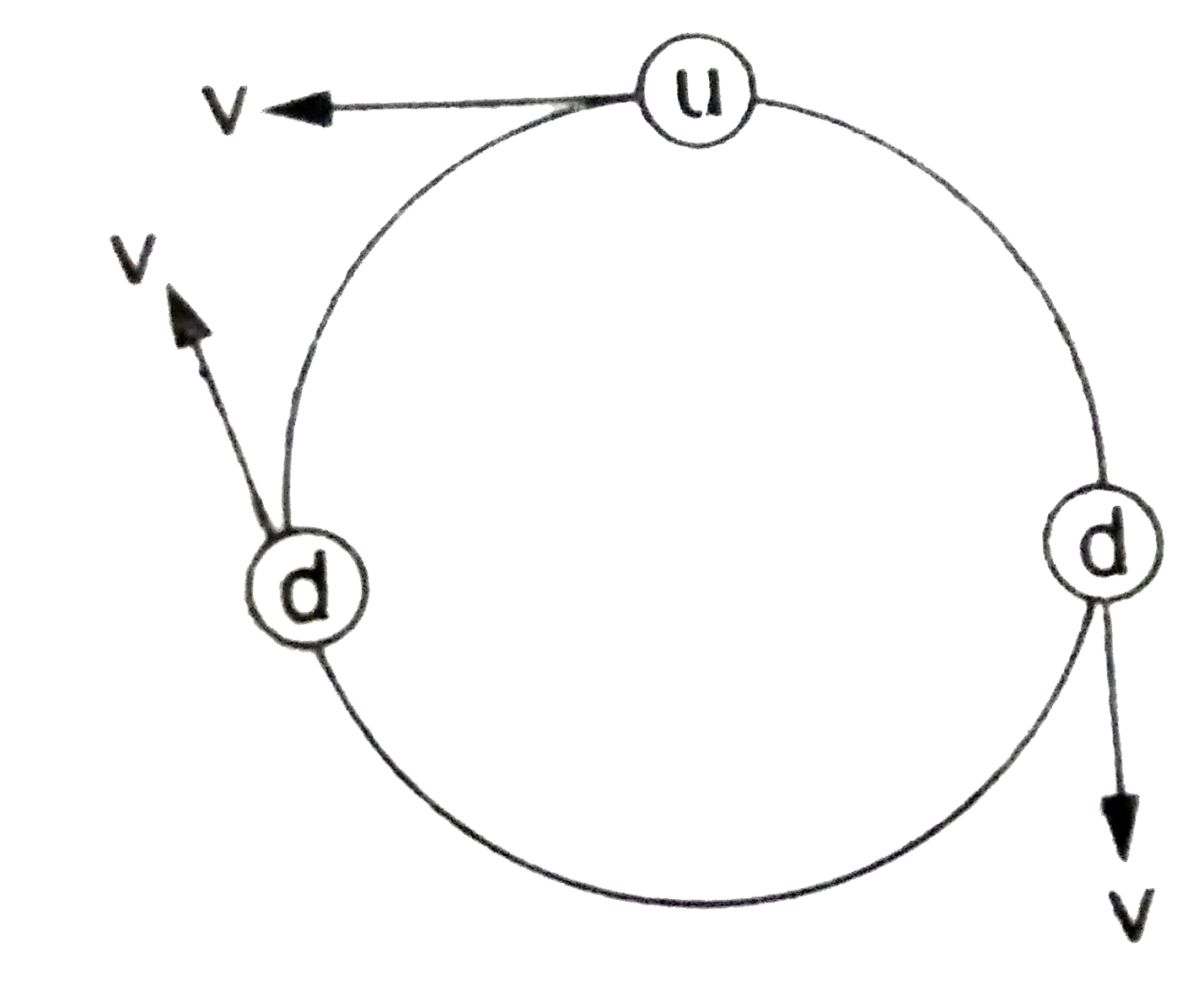
यदि क्वार्क मॉडल के तीनों क्वार्क समान दिशा में समान वृत्तीय गति उत्पन्न करें तब न्यूट्रॉन का नेट चुंबकीय आपूर्ण क्यो होगा ?06:29View Solutionनाभिक की संरचना प्रोटॉन तथा न्यूट्रॉन के कारण होती हैं , जहाँ प्रोटॉन धनावेशित कण हैं जबकि न्यूट्रॉन अनावेशित होता हैं । न्यूट्रॉन के क्वार्क मॉडल ( quark model ) के आधार पर इसका नेट आवेश शून्य रहने पर भी इसे अशून्य (nonzero) चुबंकीय आघूर्ण प्राप्त हैं जिसका z-घटक `9.66 xx 10^(-27) A - m^(2)` होता हैं । इस संकल्पना की व्याख्या न्यूट्रॉन के आंतरिक बनावट के आधार पर की जा सकती हैं । न्यूट्रॉन की सरंचना तीन प्रकार के मौलिक कणों ( fundamental particles) व्दारा होती हैं जिन्हें क्वार्क (quark) कहा जाता हैंः
एक अप क्वार्क ( up quark ) , संकेत u , आवेश + `(2e)/(3)`
दो डाउन क्वार्क ( down quark ) , संकेत d , प्रत्येक पर आवेश - `(e)/(3)`
तीन प्रकार के कणों के सम्मिलित प्रभाव से न्यूट्रॉन का नेट आवेश = `(2e)/(3) - (e)/(3) - (e)/(3) ` = शून्य । यदि ये क्वार्क गतिमान हो तब इनके व्दारा उत्पन्न चुंबकीय आघूर्ण अशून्य हो सकता हैं । चित्र में प्रदर्शित सरल मॉडल में u - क्वार्क r त्रिज्या v से वामावर्त दिशा में (anticlockwise) घूम रहा हैं तथा दोनों d - क्वार्क उसी वृतीय पथ पर समान वेग v से दक्षिणावर्त दिशा में (clockwise) घूम रहे हैं ।
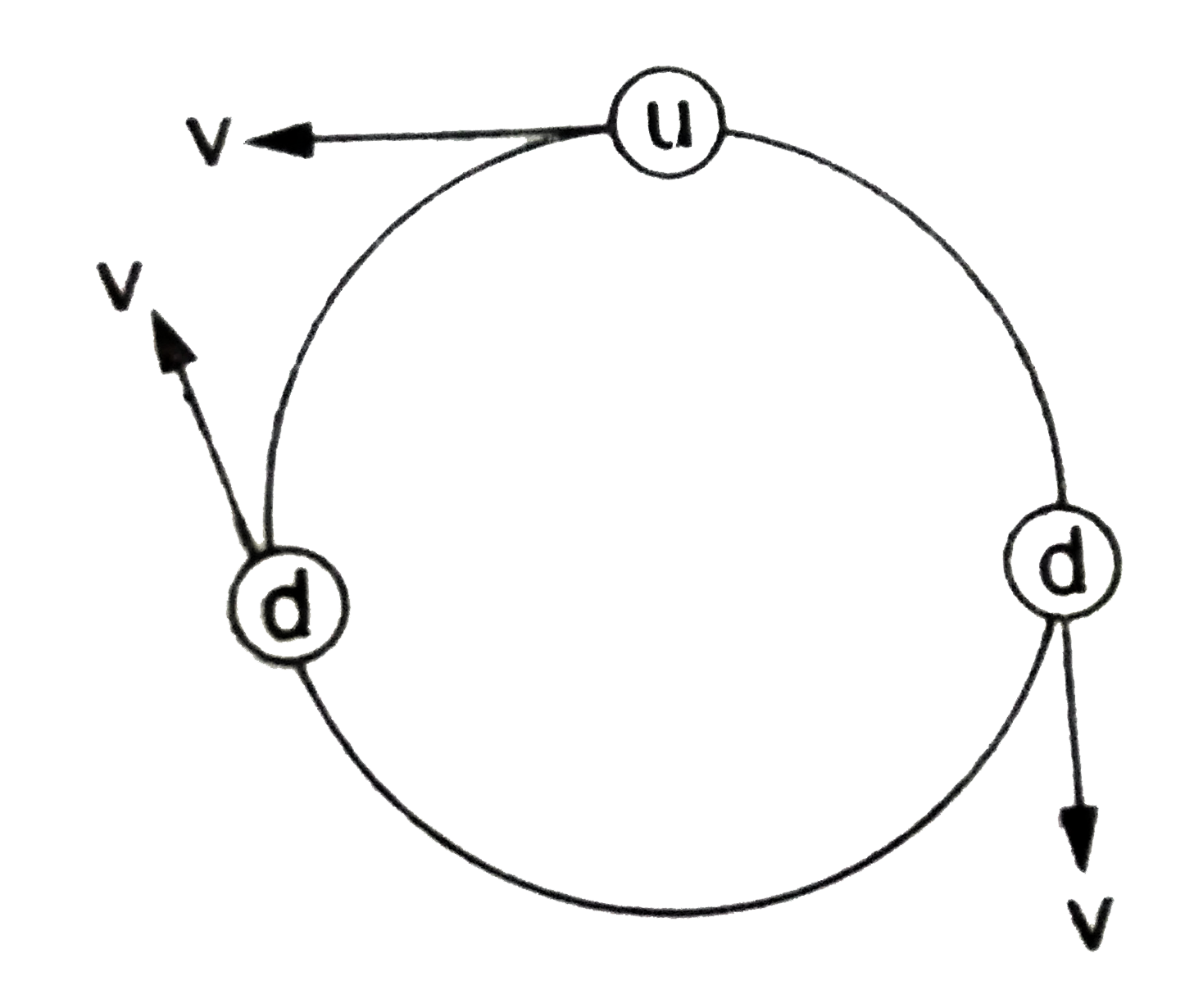
केवल एक d - क्वार्क की एकसमान वृत्तीय गति के कारण उत्पन्न चुंबकीय आपूर्ण का परिमाण06:33View Solutionनाभिक की संरचना प्रोटॉन तथा न्यूट्रॉन के कारण होती हैं , जहाँ प्रोटॉन धनावेशित कण हैं जबकि न्यूट्रॉन अनावेशित होता हैं । न्यूट्रॉन के क्वार्क मॉडल ( quark model ) के आधार पर इसका नेट आवेश शून्य रहने पर भी इसे अशून्य (nonzero) चुबंकीय आघूर्ण प्राप्त हैं जिसका z-घटक `9.66 xx 10^(-27) A - m^(2)` होता हैं । इस संकल्पना की व्याख्या न्यूट्रॉन के आंतरिक बनावट के आधार पर की जा सकती हैं । न्यूट्रॉन की सरंचना तीन प्रकार के मौलिक कणों ( fundamental particles) व्दारा होती हैं जिन्हें क्वार्क (quark) कहा जाता हैंः
एक अप क्वार्क ( up quark ) , संकेत u , आवेश + `(2e)/(3)`
दो डाउन क्वार्क ( down quark ) , संकेत d , प्रत्येक पर आवेश - `(e)/(3)`
तीन प्रकार के कणों के सम्मिलित प्रभाव से न्यूट्रॉन का नेट आवेश = `(2e)/(3) - (e)/(3) - (e)/(3) ` = शून्य । यदि ये क्वार्क गतिमान हो तब इनके व्दारा उत्पन्न चुंबकीय आघूर्ण अशून्य हो सकता हैं । चित्र में प्रदर्शित सरल मॉडल में u - क्वार्क r त्रिज्या v से वामावर्त दिशा में (anticlockwise) घूम रहा हैं तथा दोनों d - क्वार्क उसी वृतीय पथ पर समान वेग v से दक्षिणावर्त दिशा में (clockwise) घूम रहे हैं ।

केवल एक d - क्वार्क की एकसमान वृत्तीय गति के कारण उत्पन्न चुंबकीय आपूर्ण का परिमाण06:33View Solutionएकसमान चुबंकीय क्षेत्र B में चुंबक के दोलन (oscillation) का आवर्तकाल निलंबन अक्ष के परितः उसके जड़त्व - आघूर्ण ( moment of intertia) I तथा चुंबकीय आघूर्ण m पर निर्भर करता हैं और आवर्तकाल T के लिए प्रयुक्त सूत्र हैं -
`T = 2pisqrt((I)/(mB)).`
दोलन के क्रम में चुंबक की स्थितिज ऊर्जा तथा घूर्णन गतिज ऊर्जा के बीच विनिमय होता हैं तथा आदर्श स्थिति में इसकी कुल यांत्रिक ऊर्जा संरक्षित रहती हैं ।
किसी चुंबक को दो बराबर भागों में काटकर तथा उनमें विजातीय ध्रुवों ( unlike poles) , को एक साथ रखकर एकसमान चुंबकीय क्षेत्र से दोलन कराया जाता हैं । यदि काटने से पूर्व संपूर्ण चुंबक को आवर्तकाल T हो , तो उनके दो भागों से बने निकाय का आवर्तकाल क्या होगा ?07:25View Solutionएकसमान चुबंकीय क्षेत्र B में चुंबक के दोलन (oscillation) का आवर्तकाल निलंबन अक्ष के परितः उसके जड़त्व - आघूर्ण ( moment of intertia) I तथा चुंबकीय आघूर्ण m पर निर्भर करता हैं और आवर्तकाल T के लिए प्रयुक्त सूत्र हैं -
`T = 2pisqrt((I)/(mB)).`
दोलन के क्रम में चुंबक की स्थितिज ऊर्जा तथा घूर्णन गतिज ऊर्जा के बीच विनिमय होता हैं तथा आदर्श स्थिति में इसकी कुल यांत्रिक ऊर्जा संरक्षित रहती हैं ।
काटने से पहले चुबंक का आघूर्ण , क्षेत्र B की दिशा से `60^(@)` का कोण बनाता हो , तो विक्षेपित स्थिति से उसे मुक्त करने पर `theta = 0`स्थिति में चुंबक की कोणीय आवृति `Omega` क्या होगी ?02:26View Solutionएकसमान चुबंकीय क्षेत्र B में चुंबक के दोलन (oscillation) का आवर्तकाल निलंबन अक्ष के परितः उसके जड़त्व - आघूर्ण ( moment of intertia) I तथा चुंबकीय आघूर्ण m पर निर्भर करता हैं और आवर्तकाल T के लिए प्रयुक्त सूत्र हैं -
`T = 2pisqrt((I)/(mB)).`
दोलन के क्रम में चुंबक की स्थितिज ऊर्जा तथा घूर्णन गतिज ऊर्जा के बीच विनिमय होता हैं तथा आदर्श स्थिति में इसकी कुल यांत्रिक ऊर्जा संरक्षित रहती हैं ।
चुंबकीय आपूर्ण m और 2m के दो चुंबक एक - दूसरे के साथ क्रॉसित (croosed) रखे गए हैं । निलंबन अक्ष के परितः निकाय का जड़त्व - आपूर्ण l हैं । एकसमान चुबंकीय क्षेत्र B में निकाय के दोलन की आवृत्ति (Hz में ) क्या होंगी ?
 07:10View Solution
07:10View Solutionपार्थिव चुंबकत्व की व्याख्या के लिए एक काल्पनिक मॉडल प्रस्तुत किया जाता हैं जिसमें पृथ्वी के केंद्र पर स्थित m आघूर्ण का एक प्रबल चुंबक मान लेते हैं । अक्षांश (latitude)` lamda` के किसी स्थान P पर नमन कोण का मान `sigma` प्रेक्षित होता हैं । पृथ्वी की त्रिज्या R मान लें ।
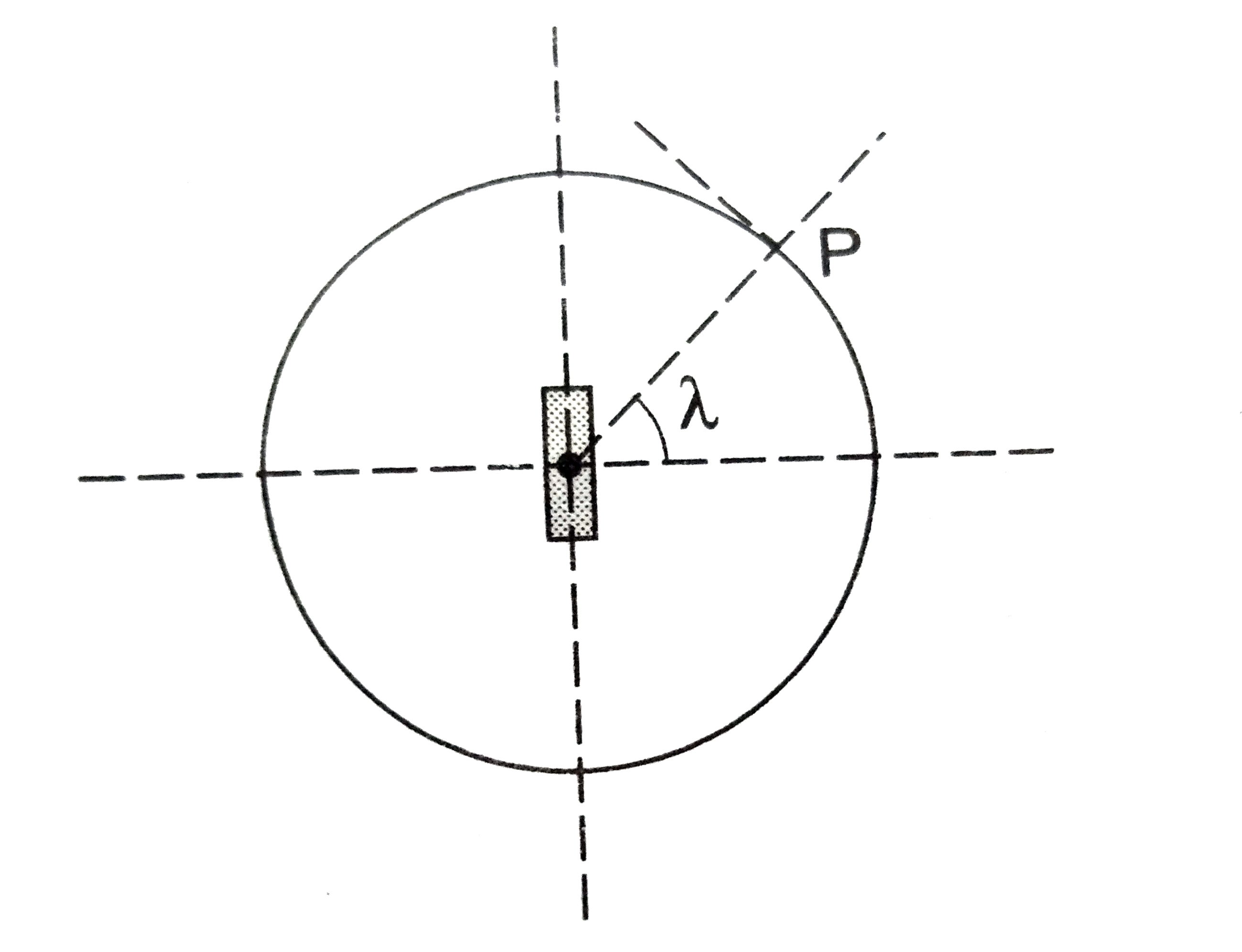
स्थान P पर पृथ्वी के चुंबकीय क्षेत्र के ऊर्ध्वाधर घटक `B_(v)` के लिए संबंध हैं03:08View Solutionपार्थिव चुंबकत्व की व्याख्या के लिए एक काल्पनिक मॉडल प्रस्तुत किया जाता हैं जिसमें पृथ्वी के केंद्र पर स्थित m आघूर्ण का एक प्रबल चुंबक मान लेते हैं । अक्षांश (latitude)` lamda` के किसी स्थान P पर नमन कोण का मान `sigma` प्रेक्षित होता हैं । पृथ्वी की त्रिज्या R मान लें ।
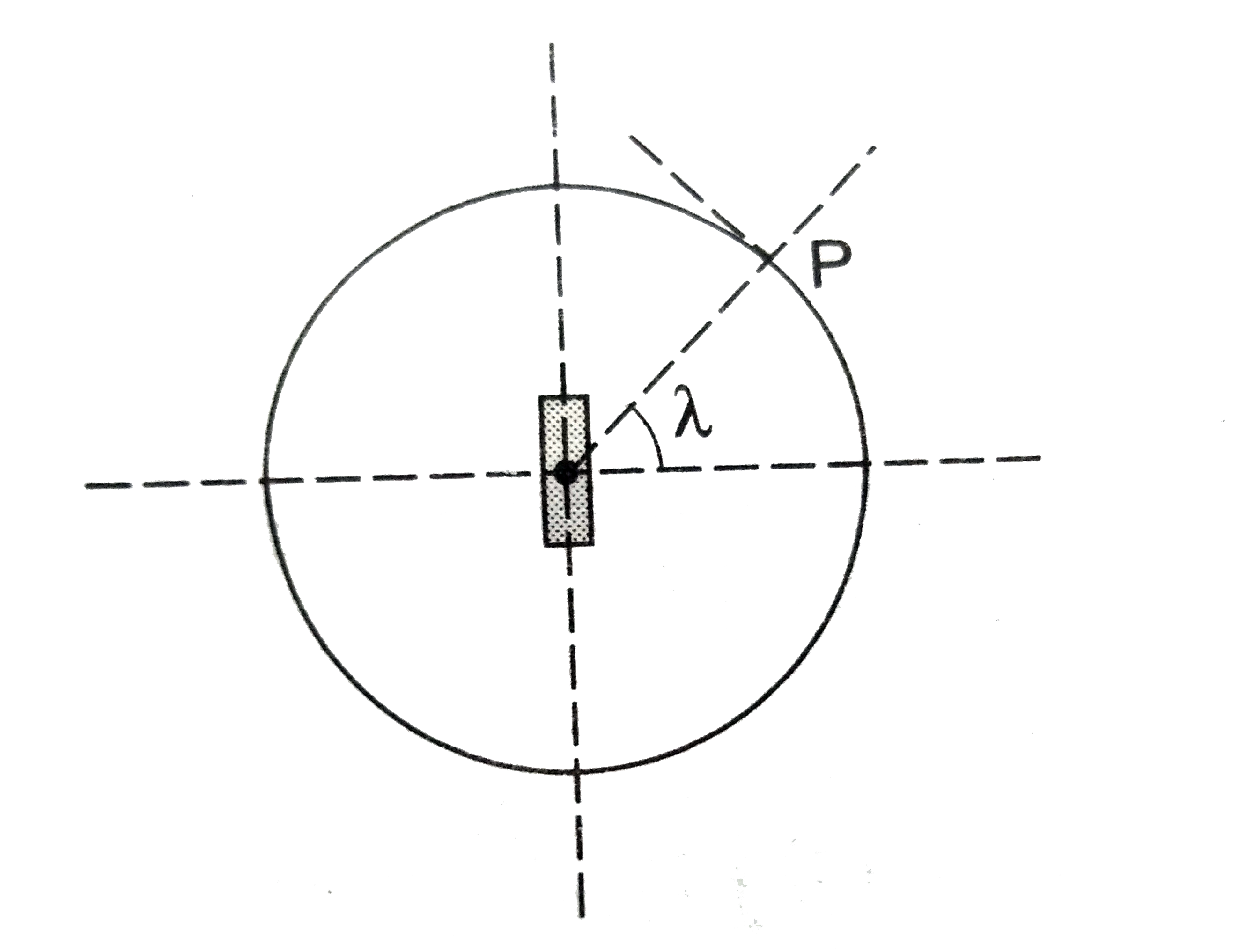
स्थान P पर पृथ्वी के चुंबकीय क्षेत्र के क्षैतिज घटक `B_(H)` के लिए संबंध हैं03:11View Solutionपार्थिव चुंबकत्व की व्याख्या के लिए एक काल्पनिक मॉडल प्रस्तुत किया जाता हैं जिसमें पृथ्वी के केंद्र पर स्थित m आघूर्ण का एक प्रबल चुंबक मान लेते हैं । अक्षांश (latitude)` lamda` के किसी स्थान P पर नमन कोण का मान `sigma` प्रेक्षित होता हैं । पृथ्वी की त्रिज्या R मान लें ।

नमन - कोण एंव अक्षांश `lamda` के बीच संबंध हैं04:12View Solutionमैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल `(c_(0) = 3xx10^(8)m s^(-1) )` से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
मुक्त आकाश में विद्युत - चुंबकीय तरंग के वेग `(c_(0))` को परावैद्युत `(in_(0))` तथा चुंबकनशीलता `(mu_(0))` के पद में किस संबंध व्दारा व्यक्त किया जाता हैं ?04:21View Solutionमैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल `(c_(0) = 3xx10^(8)m s^(-1) )` से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
चुंबकत्व में गॉस का नियम जिस समीकरण से व्यक्त होता हैं , वह हैं02:27View Solutionमैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल `(c_(0) = 3xx10^(8)m s^(-1) )` से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
स्थिर वैद्यतिकी में गॉस का नियम जिस समीकरण से व्यक्त होता हैं , वह हैं02:34View Solutionमैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल `(c_(0) = 3xx10^(8)m s^(-1) )` से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
चालन धारा `(I _(c))` तथा विस्थापन धारा `( I_(d) = epsi_(0) (d phi_(E))/(dt))` के पद में ऐम्पियर का नियम जिस समीकरण से व्यक्त होता हैं , वह हैं06:59View Solutionमैक्सवेल व्दारा प्रतिपादित क्षेत्र - समीकरणों (field equations) के आधार पर विद्युत - चुंबकीय तरंग की उत्पत्ति , संचरण तथा अन्य घटनाओं की व्याख्या की जाती हैं । इस सिध्दांत के अनुसार , विद्युत क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` एक - दूसरे से अतंरबध्द है तथा तरंग संचरण के क्रम में दोनों क्षेत्र समय के साथ परिवर्ती होते हैं । मुक्त आकाश में वे प्रकाश की चाल `(c_(0) = 3xx10^(8)m s^(-1) )` से गमन करती हैं । मैक्सवेल के चार समीकरण मूलतः (i) चुंबकत्व गॉस का नियम , (ii) स्थिर वैद्युतिकी में गॉस का नियम , (iii) फैराडे का विद्युत - चुंबकीय प्रेरण का नियम तथा
(iv) ऐम्पियर के नियम का एक पूर्ण सेट हैं ।
फैराडे का नियम जिस समीकरण में व्यक्त होता हैं , वह हैं03:12View Solutionविद्युत - चुबंकीय तरंग एक अनुप्रस्थ तरंग - गति (transverse wave - motion ) हैं जिसके विद्युत - क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` परस्पर लंबवत होते हैं तथा दोनों क्षेत्र संचरण की दिशा के भी लंबवत होते हैं । लघुतम तरंगदैर्घ्य की `gamma` - किरणों से लेकर रेडियो तरंग के विस्तृत परास तक की तरंगों से मिलकर विद्युत - चुंबकीय स्पेक्ट्रम बनता हैं । आवृत्ति तथा तरंगदैर्घ्य में इसके सभी घटक भिन्न मान के होते हैं , लेकिन निर्वात में सभी घटक के वेग समान होते हैं ।
विद्युत - चुंबकीय तरंग के संचरण की दिशा जिस संदिश की दिशा से व्यक्त होती हैं , वह हैं06:08View Solutionविद्युत - चुबंकीय तरंग एक अनुप्रस्थ तरंग - गति (transverse wave - motion ) हैं जिसके विद्युत - क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` परस्पर लंबवत होते हैं तथा दोनों क्षेत्र संचरण की दिशा के भी लंबवत होते हैं । लघुतम तरंगदैर्घ्य की `gamma` - किरणों से लेकर रेडियो तरंग के विस्तृत परास तक की तरंगों से मिलकर विद्युत - चुंबकीय स्पेक्ट्रम बनता हैं । आवृत्ति तथा तरंगदैर्घ्य में इसके सभी घटक भिन्न मान के होते हैं , लेकिन निर्वात में सभी घटक के वेग समान होते हैं ।
यदि z- दिशा में संचरित विद्युत - चुंबकीय तरंग में विद्युत - क्षेत्र आवर्ती फलन ` E_(x) = E_(0) sin (Omega t - kz)` से व्यक्त हो , तो चुंबकीय क्षेत्र के लिए प्रयुक्त आवर्ती फलन होगा06:52View Solutionविद्युत - चुबंकीय तरंग एक अनुप्रस्थ तरंग - गति (transverse wave - motion ) हैं जिसके विद्युत - क्षेत्र `vec(E)` तथा चुंबकीय क्षेत्र `vec(B)` परस्पर लंबवत होते हैं तथा दोनों क्षेत्र संचरण की दिशा के भी लंबवत होते हैं । लघुतम तरंगदैर्घ्य की `gamma` - किरणों से लेकर रेडियो तरंग के विस्तृत परास तक की तरंगों से मिलकर विद्युत - चुंबकीय स्पेक्ट्रम बनता हैं । आवृत्ति तथा तरंगदैर्घ्य में इसके सभी घटक भिन्न मान के होते हैं , लेकिन निर्वात में सभी घटक के वेग समान होते हैं ।
निम्नलिखित कथन में कौन सही हैं ?06:07View Solutionएक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण के मुड़ने का परिमाण पहले माध्यम की तुलना में दूसरे माध्यम में प्रकाश की चाल पर निर्भर करता हैं । विभिन्न माध्यमों में प्रकाश की चाल चूँकि भिन्न - भिन्न होती हैं , अतः प्रकाश की किरण की दिशा को बदलने की उनकी क्षमता भी भिन्न - भिन्न होती हैं । किसी माध्यम की प्रकाश की किरण की दिशा को बदलने की क्षमता को उसका अपवर्तनांक कहते हैं । किसी माध्यम का अपवर्तनांक n शून्य में प्रकाश की चाल c और उस माध्यम में प्रकाश की चाल `c_(m)` के अनुपात (ratio) को कहते हैं । अतः ,
`n = (c)/(c_(m))`
दो माध्यमों के निरपेक्ष अपवर्तनांकों के अनुपात को आपेक्षिक अपवर्तनांक ( relative refractive index ) कहा जाता हैं । यदि कोई माध्यम 1 एंव 2 के निरपेक्ष अपवर्तनांक क्रमशः `n_(1)` एंव `n_(2)` हो , तो माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक को प्रायः संकेत `""_(1)n_(2)` से निरुपित किया जाता हैं , इसलिए
`""_(1)n_(2) = (n_(2))/(n_(1))`.
प्रकाश को सूर्य से पृथ्वी तक पहुँचने में 8 मिनट 20 सेकंड लगता हैं । यदि सूर्य से पृथ्वी की दूरी 15 करोड़ किलोमीटर हैं , तो प्रकाश की चाल क्या होगी ?03:39View Solutionएक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण के मुड़ने का परिमाण पहले माध्यम की तुलना में दूसरे माध्यम में प्रकाश की चाल पर निर्भर करता हैं । विभिन्न माध्यमों में प्रकाश की चाल चूँकि भिन्न - भिन्न होती हैं , अतः प्रकाश की किरण की दिशा को बदलने की उनकी क्षमता भी भिन्न - भिन्न होती हैं । किसी माध्यम की प्रकाश की किरण की दिशा को बदलने की क्षमता को उसका अपवर्तनांक कहते हैं । किसी माध्यम का अपवर्तनांक n शून्य में प्रकाश की चाल c और उस माध्यम में प्रकाश की चाल `c_(m)` के अनुपात (ratio) को कहते हैं । अतः ,
`n = (c)/(c_(m))`
दो माध्यमों के निरपेक्ष अपवर्तनांकों के अनुपात को आपेक्षिक अपवर्तनांक ( relative refractive index ) कहा जाता हैं । यदि कोई माध्यम 1 एंव 2 के निरपेक्ष अपवर्तनांक क्रमशः `n_(1)` एंव `n_(2)` हो , तो माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक को प्रायः संकेत `""_(1)n_(2)` से निरुपित किया जाता हैं , इसलिए
`""_(1)n_(2) = (n_(2))/(n_(1))`.
निर्वात में प्रकाश की चाल ` 3xx10^(8)m s^(-1)` और कार्बन डाइसल्फाइड में उसकी चाल `1.80xx10^(8) m s^(-1)` हैं । कार्बन डाइसल्फाइड के अपवर्तनांक का मान होगा03:31View Solutionएक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण के मुड़ने का परिमाण पहले माध्यम की तुलना में दूसरे माध्यम में प्रकाश की चाल पर निर्भर करता हैं । विभिन्न माध्यमों में प्रकाश की चाल चूँकि भिन्न - भिन्न होती हैं , अतः प्रकाश की किरण की दिशा को बदलने की उनकी क्षमता भी भिन्न - भिन्न होती हैं । किसी माध्यम की प्रकाश की किरण की दिशा को बदलने की क्षमता को उसका अपवर्तनांक कहते हैं । किसी माध्यम का अपवर्तनांक n शून्य में प्रकाश की चाल c और उस माध्यम में प्रकाश की चाल `c_(m)` के अनुपात (ratio) को कहते हैं । अतः ,
`n = (c)/(c_(m))`
दो माध्यमों के निरपेक्ष अपवर्तनांकों के अनुपात को आपेक्षिक अपवर्तनांक ( relative refractive index ) कहा जाता हैं । यदि कोई माध्यम 1 एंव 2 के निरपेक्ष अपवर्तनांक क्रमशः `n_(1)` एंव `n_(2)` हो , तो माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक को प्रायः संकेत `""_(1)n_(2)` से निरुपित किया जाता हैं , इसलिए
`""_(1)n_(2) = (n_(2))/(n_(1))`.
1.50 अपवर्तनांक वाले काँच (glass) में प्रकाश की चाल `2xx10^(8) m s^(-1)` हो , तो 4/3 अपवर्तनांक वाले जल में प्रकाश की चाल होगी05:07View Solutionएक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण के मुड़ने का परिमाण पहले माध्यम की तुलना में दूसरे माध्यम में प्रकाश की चाल पर निर्भर करता हैं । विभिन्न माध्यमों में प्रकाश की चाल चूँकि भिन्न - भिन्न होती हैं , अतः प्रकाश की किरण की दिशा को बदलने की उनकी क्षमता भी भिन्न - भिन्न होती हैं । किसी माध्यम की प्रकाश की किरण की दिशा को बदलने की क्षमता को उसका अपवर्तनांक कहते हैं । किसी माध्यम का अपवर्तनांक n शून्य में प्रकाश की चाल c और उस माध्यम में प्रकाश की चाल `c_(m)` के अनुपात (ratio) को कहते हैं । अतः ,
`n = (c)/(c_(m))`
दो माध्यमों के निरपेक्ष अपवर्तनांकों के अनुपात को आपेक्षिक अपवर्तनांक ( relative refractive index ) कहा जाता हैं । यदि कोई माध्यम 1 एंव 2 के निरपेक्ष अपवर्तनांक क्रमशः `n_(1)` एंव `n_(2)` हो , तो माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक को प्रायः संकेत `""_(1)n_(2)` से निरुपित किया जाता हैं , इसलिए
`""_(1)n_(2) = (n_(2))/(n_(1))`.
यदि हीरे में प्रकाश की चाल निर्वात में प्रकाश की चाल का 0.42 गुना हो , तो हीरे का 1.33 अपवर्तनांक वाले जल के सापेक्ष आपेक्षिक अपवर्तनांक होगा लगभग05:34View Solutionकिसी पतले लेंस में प्रतिबिंब - दूरी (image distance) के निर्धारण के लिए उपयोगी सूत्र हैंः
`(1)/(v) - (1)/(u) = (1)/(f)`
हम जानते हैं कि वास्तविक वस्तु (real object) के लिए अवतल लेंस (concave lens ) तथा उत्तल दर्पण (convex mirror) आभासी प्रतिबिंब (virtual lens ) बनाते हैं , जबकि उत्तल लेंस (convex lens ) तथा अवतल दर्पण (concave mirror) वास्तवकि एंव आभासी दोनों प्रकार के प्रतिबिंब बना सकते हैं । एक अज्ञात लेंस के सामने एक छोटी वस्तु प्रधान अक्ष के लंबवत (perpendicularly ) निर्धारित स्थान A पर रखी जाती हैं , ताकि वस्तु से 6 गुना बड़ा प्रतिबिंब पुरानी प्रकृति का , परंतु दोगुने आकार का बने । वस्तु के स्थान में पुनः परिवर्तन कर उसे स्थिति C पर रखने पर प्रतिबिंब चौथाई आकार का रह जाता हैं । इन सभी परिस्थितियों में वस्तु को प्रधान अक्ष के लंबवत रखा जाता हैं । अब स्थिति C पर उसी वस्तु को प्रधान अक्ष के अनुरुप ( along ) क्षैतिज में इस तरह रखा जाता हैं कि बिंदु C वस्तु की लंबाई के केंद्र पर अवस्थित हो । इस तरह प्रधान अक्ष के क्षैतिज सतह पर रखने से प्रतिबंब का आवर्धन m पाया जाता हैं ।
जब वस्तु स्थिति B पर थी , तो प्रतिबिंब बना था05:49View Solutionकिसी पतले लेंस में प्रतिबिंब - दूरी (image distance) के निर्धारण के लिए उपयोगी सूत्र हैंः
`(1)/(v) - (1)/(u) = (1)/(f)`
हम जानते हैं कि वास्तविक वस्तु (real object) के लिए अवतल लेंस (concave lens ) तथा उत्तल दर्पण (convex mirror) आभासी प्रतिबिंब (virtual lens ) बनाते हैं , जबकि उत्तल लेंस (convex lens ) तथा अवतल दर्पण (concave mirror) वास्तवकि एंव आभासी दोनों प्रकार के प्रतिबिंब बना सकते हैं । एक अज्ञात लेंस के सामने एक छोटी वस्तु प्रधान अक्ष के लंबवत (perpendicularly ) निर्धारित स्थान A पर रखी जाती हैं , ताकि वस्तु से 6 गुना बड़ा प्रतिबिंब पुरानी प्रकृति का , परंतु दोगुने आकार का बने । वस्तु के स्थान में पुनः परिवर्तन कर उसे स्थिति C पर रखने पर प्रतिबिंब चौथाई आकार का रह जाता हैं । इन सभी परिस्थितियों में वस्तु को प्रधान अक्ष के लंबवत रखा जाता हैं । अब स्थिति C पर उसी वस्तु को प्रधान अक्ष के अनुरुप ( along ) क्षैतिज में इस तरह रखा जाता हैं कि बिंदु C वस्तु की लंबाई के केंद्र पर अवस्थित हो । इस तरह प्रधान अक्ष के क्षैतिज सतह पर रखने से प्रतिबंब का आवर्धन m पाया जाता हैं ।
वस्तु की स्थितियाँ A तथा B की दूरी प्रकाश - केंद्र से क्रमशः हैं05:34View Solutionकिसी पतले लेंस में प्रतिबिंब - दूरी (image distance) के निर्धारण के लिए उपयोगी सूत्र हैंः
`(1)/(v) - (1)/(u) = (1)/(f)`
हम जानते हैं कि वास्तविक वस्तु (real object) के लिए अवतल लेंस (concave lens ) तथा उत्तल दर्पण (convex mirror) आभासी प्रतिबिंब (virtual lens ) बनाते हैं , जबकि उत्तल लेंस (convex lens ) तथा अवतल दर्पण (concave mirror) वास्तवकि एंव आभासी दोनों प्रकार के प्रतिबिंब बना सकते हैं । एक अज्ञात लेंस के सामने एक छोटी वस्तु प्रधान अक्ष के लंबवत (perpendicularly ) निर्धारित स्थान A पर रखी जाती हैं , ताकि वस्तु से 6 गुना बड़ा प्रतिबिंब पुरानी प्रकृति का , परंतु दोगुने आकार का बने । वस्तु के स्थान में पुनः परिवर्तन कर उसे स्थिति C पर रखने पर प्रतिबिंब चौथाई आकार का रह जाता हैं । इन सभी परिस्थितियों में वस्तु को प्रधान अक्ष के लंबवत रखा जाता हैं । अब स्थिति C पर उसी वस्तु को प्रधान अक्ष के अनुरुप ( along ) क्षैतिज में इस तरह रखा जाता हैं कि बिंदु C वस्तु की लंबाई के केंद्र पर अवस्थित हो । इस तरह प्रधान अक्ष के क्षैतिज सतह पर रखने से प्रतिबंब का आवर्धन m पाया जाता हैं ।
लेंस की फोकस - दूरी हैंView Solutionकिसी कण का आपतित प्रकाश के एक अंश के विभिन्न दिशाओं में छितराने को प्रकाश का प्रकीर्णन ( scattering of light ) कहते हैं । जब प्रकाश छोटे सूक्ष्म कणों पर पड़ता हैं , तो उसका एक अंश विभिन्न दिशाओं में प्रकीर्णित होता हैं । प्रकाश का शेष भाग सीधे निकल जाता हैं । किसी माध्यम में छोटे - छोटे कणों के निलंबन (suspension ) को कोलॉइड कहा जाता हैं । किसी कोलॉइडीय विलयन में निलंबित कणों से प्रकाश के प्रकीर्णन को टिंडल प्रभाव (Tyndall effect) कहा जाता हैं । किसी कण से प्रकीर्णित प्रकाश का रंग उसके आकार (size) पर निर्भर करता हैं । अतिसूक्ष्म कण अधिक तरंगदैर्घ्य के प्रकाश की अपेक्षा कम तरंगदैर्घ्य के प्रकाश को अधिक अच्छी तरह प्रकीर्णित करते हैं । हम जानते हैं कि नीले रंग का तरंगदैर्घ्य कम होता हैं और लाल रंग का अधिक । अतः , जब श्वेत प्रकाश ( white light) सूक्ष्म कणों पर पड़ता हैं तो नीले रंग का प्रकीर्णन अधिक होता हैं और लाल रंग का बहुत कम प्रकीर्णन होता हैं । जैसे - जैसे कणों का आकार ( size ) बढ़ता हैं , अधिक तरंगदैर्घ्य का प्रकाश भी बढ़ता हैं । बड़े कण सभी तरंगदैर्घ्य के प्रकाश का समान रुप से प्रकीर्णन करते हैं
श्वेत प्रकाश के किस वर्ण (रंग ) के लिए तरंगदैर्घ्य अधिकतम होता हैं ?07:32View Solutionकिसी कण का आपतित प्रकाश के एक अंश के विभिन्न दिशाओं में छितराने को प्रकाश का प्रकीर्णन ( scattering of light ) कहते हैं । जब प्रकाश छोटे सूक्ष्म कणों पर पड़ता हैं , तो उसका एक अंश विभिन्न दिशाओं में प्रकीर्णित होता हैं । प्रकाश का शेष भाग सीधे निकल जाता हैं । किसी माध्यम में छोटे - छोटे कणों के निलंबन (suspension ) को कोलॉइड कहा जाता हैं । किसी कोलॉइडीय विलयन में निलंबित कणों से प्रकाश के प्रकीर्णन को टिंडल प्रभाव (Tyndall effect) कहा जाता हैं । किसी कण से प्रकीर्णित प्रकाश का रंग उसके आकार (size) पर निर्भर करता हैं । अतिसूक्ष्म कण अधिक तरंगदैर्घ्य के प्रकाश की अपेक्षा कम तरंगदैर्घ्य के प्रकाश को अधिक अच्छी तरह प्रकीर्णित करते हैं । हम जानते हैं कि नीले रंग का तरंगदैर्घ्य कम होता हैं और लाल रंग का अधिक । अतः , जब श्वेत प्रकाश ( white light) सूक्ष्म कणों पर पड़ता हैं तो नीले रंग का प्रकीर्णन अधिक होता हैं और लाल रंग का बहुत कम प्रकीर्णन होता हैं । जैसे - जैसे कणों का आकार ( size ) बढ़ता हैं , अधिक तरंगदैर्घ्य का प्रकाश भी बढ़ता हैं । बड़े कण सभी तरंगदैर्घ्य के प्रकाश का समान रुप से प्रकीर्णन करते हैं |
निम्नलिखित कथन में कौन गलत हैं ?09:06View Solutionकिसी कण का आपतित प्रकाश के एक अंश के विभिन्न दिशाओं में छितराने को प्रकाश का प्रकीर्णन ( scattering of light ) कहते हैं । जब प्रकाश छोटे सूक्ष्म कणों पर पड़ता हैं , तो उसका एक अंश विभिन्न दिशाओं में प्रकीर्णित होता हैं । प्रकाश का शेष भाग सीधे निकल जाता हैं । किसी माध्यम में छोटे - छोटे कणों के निलंबन (suspension ) को कोलॉइड कहा जाता हैं । किसी कोलॉइडीय विलयन में निलंबित कणों से प्रकाश के प्रकीर्णन को टिंडल प्रभाव (Tyndall effect) कहा जाता हैं । किसी कण से प्रकीर्णित प्रकाश का रंग उसके आकार (size) पर निर्भर करता हैं । अतिसूक्ष्म कण अधिक तरंगदैर्घ्य के प्रकाश की अपेक्षा कम तरंगदैर्घ्य के प्रकाश को अधिक अच्छी तरह प्रकीर्णित करते हैं । हम जानते हैं कि नीले रंग का तरंगदैर्घ्य कम होता हैं और लाल रंग का अधिक । अतः , जब श्वेत प्रकाश ( white light) सूक्ष्म कणों पर पड़ता हैं तो नीले रंग का प्रकीर्णन अधिक होता हैं और लाल रंग का बहुत कम प्रकीर्णन होता हैं । जैसे - जैसे कणों का आकार ( size ) बढ़ता हैं , अधिक तरंगदैर्घ्य का प्रकाश भी बढ़ता हैं । बड़े कण सभी तरंगदैर्घ्य के प्रकाश का समान रुप से प्रकीर्णन करते हैं |
निम्नलिखित में कौन - सा कथन गलत हैं ?09:46View Solutionकिसी कण का आपतित प्रकाश के एक अंश के विभिन्न दिशाओं में छितराने को प्रकाश का प्रकीर्णन ( scattering of light ) कहते हैं । जब प्रकाश छोटे सूक्ष्म कणों पर पड़ता हैं , तो उसका एक अंश विभिन्न दिशाओं में प्रकीर्णित होता हैं । प्रकाश का शेष भाग सीधे निकल जाता हैं । किसी माध्यम में छोटे - छोटे कणों के निलंबन (suspension ) को कोलॉइड कहा जाता हैं । किसी कोलॉइडीय विलयन में निलंबित कणों से प्रकाश के प्रकीर्णन को टिंडल प्रभाव (Tyndall effect) कहा जाता हैं । किसी कण से प्रकीर्णित प्रकाश का रंग उसके आकार (size) पर निर्भर करता हैं । अतिसूक्ष्म कण अधिक तरंगदैर्घ्य के प्रकाश की अपेक्षा कम तरंगदैर्घ्य के प्रकाश को अधिक अच्छी तरह प्रकीर्णित करते हैं । हम जानते हैं कि नीले रंग का तरंगदैर्घ्य कम होता हैं और लाल रंग का अधिक । अतः , जब श्वेत प्रकाश ( white light) सूक्ष्म कणों पर पड़ता हैं तो नीले रंग का प्रकीर्णन अधिक होता हैं और लाल रंग का बहुत कम प्रकीर्णन होता हैं । जैसे - जैसे कणों का आकार ( size ) बढ़ता हैं , अधिक तरंगदैर्घ्य का प्रकाश भी बढ़ता हैं । बड़े कण सभी तरंगदैर्घ्य के प्रकाश का समान रुप से प्रकीर्णन करते हैं |
निम्नलिखित में कौन - सा कथन गलत हैं ?09:46View Solution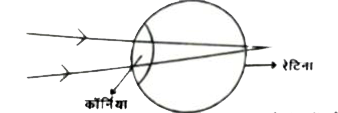
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
सामान्य दोषमुक्त आखों में कॉर्निया से कितनी दूरी पर रेटिना होना चाहिए ?09:06View Solution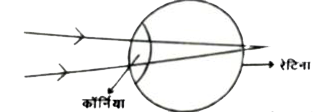
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
निकट दिष्टि एवं दूरी दिष्टि दोष को दूर करने के लिए क्रमशः किस प्रकृति का लेंस उपयोग किया जाना चाहिए ? [ मान लें कि `f_(c)=x`]07:13View Solution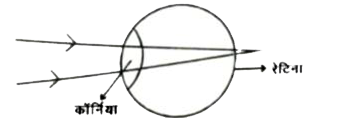
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
एक व्यक्ति के कॉर्निया की फोकस दूरी 1.8 सेमी है , तथा वह दिष्टीदोष से मुक्त हेतु एक `f=-16.5` सेमी के संशोधी लेंस को आंख के कॉर्निया से `x=1.5` सेमी की दूरी पर उपयोग करता है। ऐसी स्थिति में दूरस्थ वस्तु से आने वाली किरणों का कॉर्निया से प्रतिबिम्ब दूरी होगी :06:26View Solutionलेंस एक पारदर्शी पदार्थ की दो सतहों से घिरा क्षेत्र हैं , जिनमें कम से कम एक सतह वक्र होती हैं । लेंस की दोनों सतहें भी वक्र हो सकती हैं । सभी दूरियों को प्रकाश केंद्र से मापा जाता हैं । आपतित किरण की दिशा धनात्मक मानी जाती हैं , जबकि आपतित किरण की विपरीत दिशा ऋणात्मक मानी जाती हैं । गोलीय वक्र सतह पर अपवर्तन - सूत्र होता हैं - `(mu_(2))/(v) - (mu_(1))/(u) = (mu_(2) - mu_(1))/(r) ` तथा लेंस के लिए गाउस सूत्र (Gauss' s formula ) है - `(1)/(v) - (1)/(u) = (1)/(f)`.
लेंस की इन सतहों से विभिन्न आकार एंव प्रकृति के प्रतिबिंब बनते हैं तथा प्रतिबिंब की प्रकृति एंव आकार लेंस की अपवर्तक सतहों से वस्तु की दूरी पर निर्भर करते हैं ।
किसी व्दि - उत्तल (biconvex) लेंस की प्रत्येक सतह की वक्रता - त्रिज्या का मान `|r_(1)| = |r_(2)| = 40 cm` तथा लेंस के पदार्थ का अपवर्तनांक ` mu = (3)/(2)` हैं , तो इसकी क्षमता (power) होगी09:16View Solutionलेंस एक पारदर्शी पदार्थ की दो सतहों से घिरा क्षेत्र हैं , जिनमें कम से कम एक सतह वक्र होती हैं । लेंस की दोनों सतहें भी वक्र हो सकती हैं । सभी दूरियों को प्रकाश केंद्र से मापा जाता हैं । आपतित किरण की दिशा धनात्मक मानी जाती हैं , जबकि आपतित किरण की विपरीत दिशा ऋणात्मक मानी जाती हैं । गोलीय वक्र सतह पर अपवर्तन - सूत्र होता हैं - `(mu)/(v) - (mu)/(u) = (mu_(2) - mu_(1))/(r) ` तथा लेंस के लिए गाउस सूत्र (Gauss' s formula ) है - `(1)/(v) - (1)/(u) = (1)/(f)`.
लेंस की इन सतहों से विभिन्न आकार एंव प्रकृति के प्रतिबिंब बनते हैं तथा प्रतिबिंब की प्रकृति एंव आकार लेंस की अपवर्तक सतहों से वस्तु की दूरी पर निर्भर करते हैं ।
20 cm फोकस - दूरी वाले अभिसारी लेंस (converging lens) से वस्तु के दुगुने आकार का वास्तविक प्रतिबिंब प्राप्त करने के लिए वस्तु का लेंस से जिस दूरी पर रखना होगा , वह हैं04:16View Solutionनिम्नलिखित प्रश्न संख्या 23 से 25 तक के लिए एक उद्धरण दिया गया है। पहले प्रदत्त उद्धरण को ध्यान से पढ़ें तत्पश्चात् दिये गये तीन प्रश्नों का सही उत्तर दिये गये विकल्प तीनों प्रश्न दो-दो अंक के हैं में से चुनें।
उदरण : लेंस एक पारदशी पदार्थ की दो सतहों से घिरा क्षेत्र है, जिनमें कम-से-कम एक सतह लेंस के दोनों सतहें भी वक्र हो सकती हैं। सभी दरियों को प्रकाश केन्द्र मापा जाता है। आपतित किरण की दिशा धनात्मक मानी जाती है. जबकि आपतित की उल्टी दिशा ऋणात्मक मानी जाती है।
गोलीय वक्र सतह पर अपवर्तन-सूत्र होता है
`(n_(2))/(V)-(n_(1))/(u)=(n_(2)-n_(1))/(r)`तथा लेंस के लिए गाउस का सूत्र है : `(1)/(V)-(1)/(u)=(1)/(f)`
लेंस के इन सतहों से विभिन्न आकार एवं प्रकृति के प्रतिबिम्ब बनते हैं तथा प्रतिबिम्ब की एवं आकार लेस को अपवर्तक सतहों से वस्तु की दूरी पर निर्भर करते हैं।
जब तक अभिसारी लेंस को एक ऐसे द्रव में डुबाया जाता है, जिसका अपवर्तनांक लेंस के पदार्थ के अपवर्तनांक के बराबर होता है `(n_(द्रव) = n_(लेंस))` तो लेंस की फोकस दूरी :05:38View Solutionसर जे0 जे0 थॉमसन ने इलेक्ट्रॉन के विशिष्ट आवेश (specific charge) `(e)/(m_(e))` को मापने के लिए एक प्रयोग किया था , जिसका आधुनिक स्वरुप चित्र में प्रदर्शित किया गया हैं ।
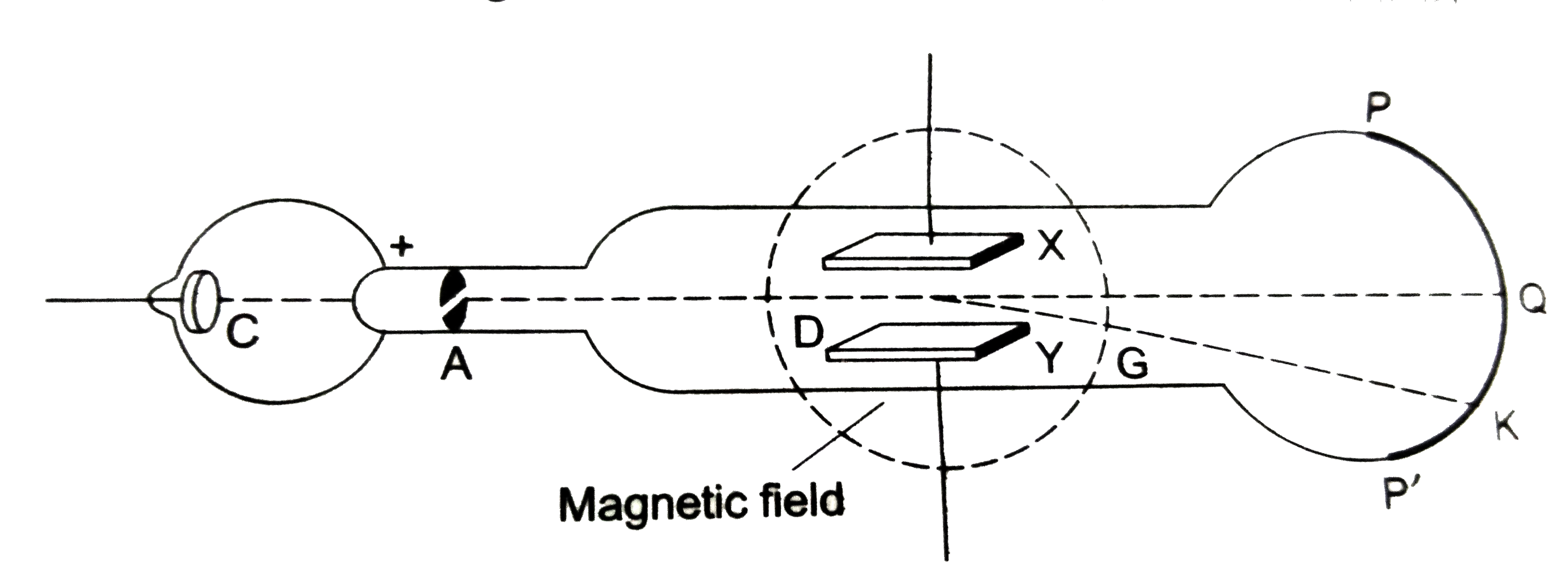
एक तापायनिक उत्सर्जन (thermonic emission ) से इलेक्ट्रॉन उत्पन्न कर उसे विभवांतर V के अंतर्गत त्वरित किया जाता हैं । इलेक्ट्रॉन विक्षेपण उत्पन्न करनेवाले प्लेटों ( deflecting plates ) के विद्युतीय - क्षेत्र `vec (E)` एंव चुंबकीय क्षेत्र `vec (B) ` से होकर गुजरता हैं । प्लेटों से बाहर निकलने पर विद्युतीय एंव चुंबकीय प्रभाव रहित क्षेत्र से गुजरकर पर्दे पर पड़ता हैं । इलेक्ट्रॉन के गमन वाले पूरे क्षेत्र को निर्वात ( vacuum) बनाया जाता हैं ।
प्रारंभ में थॉमसन ने E = 0 तथा B = 0 के लिए पर्दे ( screen ) पर बिना विक्षेपित इलेक्ट्रॉन के स्थान को चिह्नित किया । इसके लिए विद्युत क्षेत्र `vec (E)` को उत्पन्न किया गया । इससे इलेक्ट्रॉन के प्रवाह मार्ग में उत्पन्न विक्षेप,
`d_(1) = (e EL^(2))/(2m_(e)v^(2))`
को मापा गया , जहाँ L प्लेटों की लंबाई एंव v इलेक्ट्रॉन का वेग हैं । इसके बाद चुंबकीय क्षेत्र `vec (B)` के मान को इस प्रकार समंजित किया जाता हैं , ताकि पर्दे पर इलेक्ट्रॉन का विक्षेप शून्य हो जाए । ऐसी स्थिति में
eE = evB.
इस संबंध से v के मान को `d_(1)` के मान वाले समीकरण में पदस्थापित करने पर ,
`(e)/(m_(e)) = (2d_(1)E)/(B^(2)L^(2))` .
थॉमसन के लिए इलेक्ट्रॉन - प्रवाह मार्ग को निर्वात बनाने की आवश्यकता क्यों पड़ी ?06:24View Solutionसर जे0 जे0 थॉमसन ने इलेक्ट्रॉन के विशिष्ट आवेश (specific charge) `(e)/(m_(e))` को मापने के लिए एक प्रयोग किया था , जिसका आधुनिक स्वरुप चित्र में प्रदर्शित किया गया हैं ।
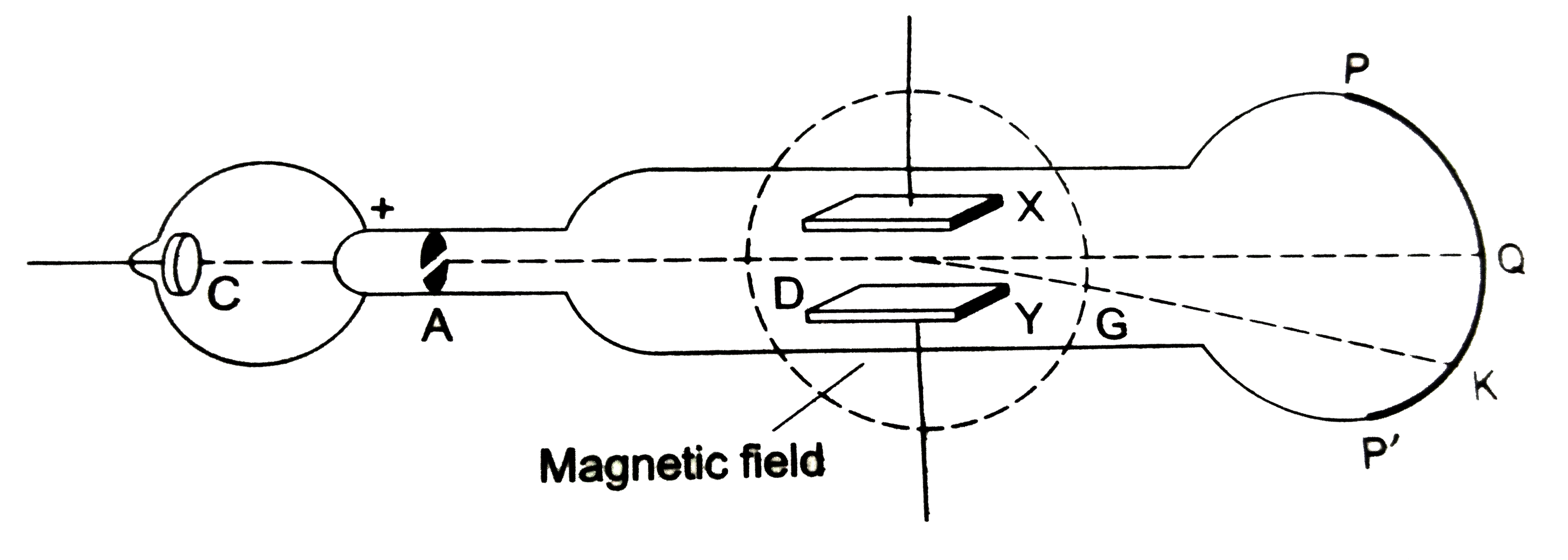
एक तापायनिक उत्सर्जन (thermonic emission ) से इलेक्ट्रॉन उत्पन्न कर उसे विभवांतर V के अंतर्गत त्वरित किया जाता हैं । इलेक्ट्रॉन विक्षेपण उत्पन्न करनेवाले प्लेटों ( deflecting plates ) के विद्युतीय - क्षेत्र `vec (E)` एंव चुंबकीय क्षेत्र `vec (B) ` से होकर गुजरता हैं । प्लेटों से बाहर निकलने पर विद्युतीय एंव चुंबकीय प्रभाव रहित क्षेत्र से गुजरकर पर्दे पर पड़ता हैं । इलेक्ट्रॉन के गमन वाले पूरे क्षेत्र को निर्वात ( vacuum) बनाया जाता हैं ।
प्रारंभ में थॉमसन ने E = 0 तथा B = 0 के लिए पर्दे ( screen ) पर बिना विक्षेपित इलेक्ट्रॉन के स्थान को चिह्नित किया । इसके लिए विद्युत क्षेत्र `vec (E)` को उत्पन्न किया गया । इससे इलेक्ट्रॉन के प्रवाह मार्ग में उत्पन्न विक्षेप,
`d_(1) = (e EL^(2))/(2m_(e)v^(2))`
को मापा गया , जहाँ L प्लेटों की लंबाई एंव v इलेक्ट्रॉन का वेग हैं । इसके बाद चुंबकीय क्षेत्र `vec (B)` के मान को इस प्रकार समंजित किया जाता हैं , ताकि पर्दे पर इलेक्ट्रॉन का विक्षेप शून्य हो जाए । ऐसी स्थिति में
eE = evB.
इस संबंध से v के मान को `d_(1)` के मान वाले समीकरण में पदस्थापित करने पर ,
`(e)/(m_(e)) = (2d_(1)E)/(B^(2)L^(2))` .
अगर विभवांतर को बढ़ाकर इलेक्ट्रॉन की चाल को दोगुना कर दिया गया होता तो निम्नलिखित में कौन - सा कथन `(e)/(m)` के सही मापन के लिए आवश्यक होता ?07:10View Solutionसर जे0 जे0 थॉमसन ने इलेक्ट्रॉन के विशिष्ट आवेश (specific charge) `(e)/(m_(e))` को मापने के लिए एक प्रयोग किया था , जिसका आधुनिक स्वरुप चित्र में प्रदर्शित किया गया हैं ।
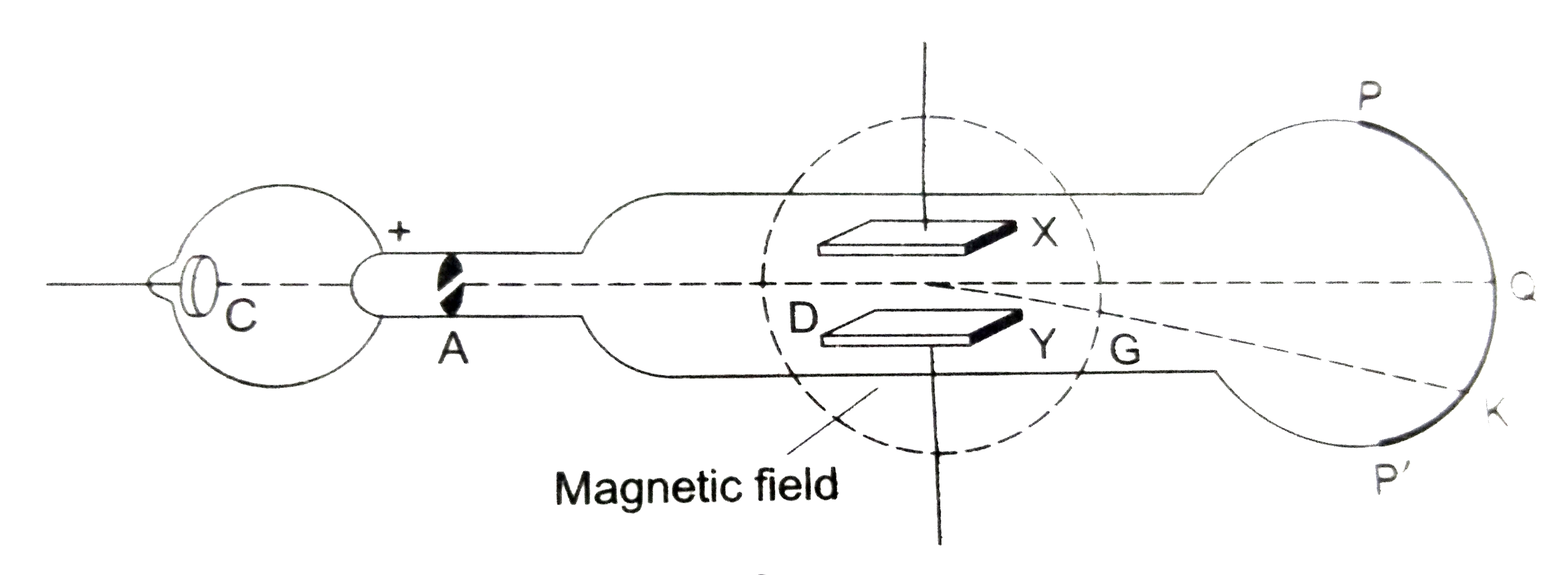
एक तापायनिक उत्सर्जन (thermonic emission ) से इलेक्ट्रॉन उत्पन्न कर उसे विभवांतर V के अंतर्गत त्वरित किया जाता हैं । इलेक्ट्रॉन विक्षेपण उत्पन्न करनेवाले प्लेटों ( deflecting plates ) के विद्युतीय - क्षेत्र `vec (E)` एंव चुंबकीय क्षेत्र `vec (B) ` से होकर गुजरता हैं । प्लेटों से बाहर निकलने पर विद्युतीय एंव चुंबकीय प्रभाव रहित क्षेत्र से गुजरकर पर्दे पर पड़ता हैं । इलेक्ट्रॉन के गमन वाले पूरे क्षेत्र को निर्वात ( vacuum) बनाया जाता हैं ।
प्रारंभ में थॉमसन ने E = 0 तथा B = 0 के लिए पर्दे ( screen ) पर बिना विक्षेपित इलेक्ट्रॉन के स्थान को चिह्नित किया । इसके लिए विद्युत क्षेत्र `vec (E)` को उत्पन्न किया गया । इससे इलेक्ट्रॉन के प्रवाह मार्ग में उत्पन्न विक्षेप,
`d_(1) = (e EL^(2))/(2m_(e)v^(2))`
को मापा गया , जहाँ L प्लेटों की लंबाई एंव v इलेक्ट्रॉन का वेग हैं । इसके बाद चुंबकीय क्षेत्र `vec (B)` के मान को इस प्रकार समंजित किया जाता हैं , ताकि पर्दे पर इलेक्ट्रॉन का विक्षेप शून्य हो जाए । ऐसी स्थिति में
eE = evB.
इस संबंध से v के मान को `d_(1)` के मान वाले समीकरण में पदस्थापित करने पर ,
`(e)/(m_(e)) = (2d_(1)E)/(B^(2)L^(2))` .
यदि प्रयुक्त यंत्र में विद्युत - क्षेत्र लगाने पर इलेक्ट्रॉन नीचे की ओर विक्षेपित हुआ होता , तब प्रयोग के दूसरे चरण में प्रयुक्त विद्युतीय क्षेत्र `vec(E)` एंव चुंबकीय क्षेत्र `vec (B)` की दिशाएँ होती06:41View Solutionप्रकाश - ऊर्जा व्दारा किसी धातु के पृष्ठ से इलेक्ट्रॉन के उत्सर्जन को प्रकाश - वैद्युत प्रभाव कहते हैं तथा इस प्रकार निर्गत इलेक्ट्रॉनों को प्रकाश - इलेक्ट्रॉन कहते हैं । दिए गए धातु के लिए यदि आपतित प्रकाश की आवृत्ति एक निश्चित न्यूनतम मान से कम हो , तो प्रकाश इलेक्ट्रॉन उत्सर्जित नही होते । आपतित प्रकाश की वह न्यूनतम आवृत्ति जिससे दिए गए धातु से इलेक्ट्रॉन उत्सर्जित हो सकते हैं , देहली आवृत्ति ( threshold frequency ) कहलाती हैं । उत्सर्जित इलेक्ट्रॉनों की गतिज ऊर्जा शून्य से एक अधिकतम मान तक होती हैं । यदि धातु का कार्य फलन `phi_(0) ` हो तथा आपतित प्रकाश की आवृत्ति v अथवा तरंगदैर्घ्य `lamda` हो , तो उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ,`E_(k) = hv - phi_(0) = (hc)/(lamda) - phi_(0)`. यह आंइस्टीन का प्रकाश - वैद्युत समीकरण कहलाता हैं । यदि देहली आवृत्ति `v_(0)` तथा देहली तरंगदैर्घ्य `lamda_(0)` हो , तो धातु का कार्य - फलन , ` phi_(0) = hv_(0) = (hc)/(lamda_(0))` . यदि उत्सर्जित इलेक्ट्रानों की अधिकतम गतिज ऊर्जा `E_(k)`हो , तो निरोधी विभव (stopping potential ) `v_(0)` के लिए `E_(k) = (1)/(2)mv_(max)^(2) = eV_(0)` जिसमें `v_(max)` प्रकाश - इलेक्ट्रॉनों की अधिकतम चाल हैं ।
जब 400 nm तरंगदैर्घ्य वाला बैंगनी प्रकाश एक प्रकाश - वैद्युत सेल पर गिरता हैं , तो इसके कैथोड़ से इलेक्ट्रॉन की गति रोकने के लिए `0.5 eV` के निरोधी विभव की आवश्यकता होती हैं । यदि h `= 6.6 xx 10^(-34)` Js हो , तो
इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा होगी04:31View Solutionप्रकाश - ऊर्जा व्दारा किसी धातु के पृष्ठ से इलेक्ट्रॉन के उत्सर्जन को प्रकाश - वैद्युत प्रभाव कहते हैं तथा इस प्रकार निर्गत इलेक्ट्रॉनों को प्रकाश - इलेक्ट्रॉन कहते हैं । दिए गए धातु के लिए यदि आपतित प्रकाश की आवृत्ति एक निश्चित न्यूनतम मान से कम हो , तो प्रकाश इलेक्ट्रॉन उत्सर्जित नही होते । आपतित प्रकाश की वह न्यूनतम आवृत्ति जिससे दिए गए धातु से इलेक्ट्रॉन उत्सर्जित हो सकते हैं , देहली आवृत्ति ( threshold frequency ) कहलाती हैं । उत्सर्जित इलेक्ट्रॉनों की गतिज ऊर्जा शून्य से एक अधिकतम मान तक होती हैं । यदि धातु का कार्य फलन `phi_(0) ` हो तथा आपतित प्रकाश की आवृत्ति v अथवा तरंगदैर्घ्य `lamda` हो , तो उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ,
`E_(k) = hv - phi_(0) = (hc)/(lamda) - phi_(0)`.
यह आंइस्टीन का प्रकाश - वैद्युत समीकरण कहलाता हैं । यदि देहली आवृत्ति `v_(0)` तथा देहली तरंगदैर्घ्य `lamda_(0)` हो , तो धातु का कार्य - फलन ,
` phi_(0) = hv_(0) = (hc)/(lamda_(0))` . यदि उत्सर्जित इलेक्ट्रानों की अधिकतम गतिज ऊर्जा `E_(k)`हो , तो निरोधी विभव (stopping potential ) `V_(0)` के लिए
`E_(k) = (1)/(2)mv_(max)^(2) = eV_(0)` जिसमें `v_(max)` प्रकाश - इलेक्ट्रॉनों की अधिकतम चाल हैं । जब 400 nm तरंगदैर्घ्य वाला बैंगनी प्रकाश एक प्रकाश - वैद्युत सेल पर गिरता हैं , तो इसके कैथोड़ से इलेक्ट्रॉन की गति रोकने के लिए `0.5 eV` के निरोधी विभव की आवश्यकता होती हैं । यदि h `= 6.6 xx 10^(-34)` Js हो , तो
आपतित फोटॉनों की ऊर्जा होगी03:31View Solutionप्रकाश - ऊर्जा व्दारा किसी धातु के पृष्ठ से इलेक्ट्रॉन के उत्सर्जन को प्रकाश - वैद्युत प्रभाव कहते हैं तथा इस प्रकार निर्गत इलेक्ट्रॉनों को प्रकाश - इलेक्ट्रॉन कहते हैं । दिए गए धातु के लिए यदि आपतित प्रकाश की आवृत्ति एक निश्चित न्यूनतम मान से कम हो , तो प्रकाश इलेक्ट्रॉन उत्सर्जित नही होते । आपतित प्रकाश की वह न्यूनतम आवृत्ति जिससे दिए गए धातु से इलेक्ट्रॉन उत्सर्जित हो सकते हैं , देहली आवृत्ति ( threshold frequency ) कहलाती हैं । उत्सर्जित इलेक्ट्रॉनों की गतिज ऊर्जा शून्य से एक अधिकतम मान तक होती हैं । यदि धातु का कार्य फलन `phi_(0) ` हो तथा आपतित प्रकाश की आवृत्ति v अथवा तरंगदैर्घ्य `lamda` हो , तो उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ,
`E_(k) = hv - phi_(0) = (hc)/(lamda) - phi_(0)`.
यह आंइस्टीन का प्रकाश - वैद्युत समीकरण कहलाता हैं । यदि देहली आवृत्ति `v_(0)` तथा देहली तरंगदैर्घ्य `lamda_(0)` हो , तो धातु का कार्य - फलन ,
` phi_(0) = hv_(0) = (hc)/(lamda_(0))` . यदि उत्सर्जित इलेक्ट्रानों की अधिकतम गतिज ऊर्जा `E_(k)`हो , तो निरोधी विभव (stopping potential ) `v_(0)` के लिए
`E_(k) = (1)/(2)mv_(max)^(2) = eV_(0)` जिसमें `v_(max)` प्रकाश - इलेक्ट्रॉनों की अधिकतम चाल हैं । जब 400 nm तरंगदैर्घ्य वाला बैंगनी प्रकाश एक प्रकाश - वैद्युत सेल पर गिरता हैं , तो इसके कैथोड़ से इलेक्ट्रॉन की गति रोकने के लिए `0.5 eV` के निरोधी विभव की आवश्यकता होती हैं । यदि h `= 6.6 xx 10^(-34)` Js हो , तो
इस सेल के लिए कार्य - फलन हैं05:35View Solutionप्रकाश - ऊर्जा व्दारा किसी धातु के पृष्ठ से इलेक्ट्रॉन के उत्सर्जन को प्रकाश - वैद्युत प्रभाव कहते हैं तथा इस प्रकार निर्गत इलेक्ट्रॉनों को प्रकाश - इलेक्ट्रॉन कहते हैं । दिए गए धातु के लिए यदि आपतित प्रकाश की आवृत्ति एक निश्चित न्यूनतम मान से कम हो , तो प्रकाश इलेक्ट्रॉन उत्सर्जित नही होते । आपतित प्रकाश की वह न्यूनतम आवृत्ति जिससे दिए गए धातु से इलेक्ट्रॉन उत्सर्जित हो सकते हैं , देहली आवृत्ति ( threshold frequency ) कहलाती हैं । उत्सर्जित इलेक्ट्रॉनों की गतिज ऊर्जा शून्य से एक अधिकतम मान तक होती हैं । यदि धातु का कार्य फलन `phi_(0) ` हो तथा आपतित प्रकाश की आवृत्ति v अथवा तरंगदैर्घ्य `lamda` हो , तो उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ,
`E_(k) = hv - phi_(0) = (hc)/(lamda) - phi_(0)`.
यह आंइस्टीन का प्रकाश - वैद्युत समीकरण कहलाता हैं । यदि देहली आवृत्ति `v_(0)` तथा देहली तरंगदैर्घ्य `lamda_(0)` हो , तो धातु का कार्य - फलन ,
` phi_(0) = hv_(0) = (hc)/(lamda_(0))` . यदि उत्सर्जित इलेक्ट्रानों की अधिकतम गतिज ऊर्जा `E_(k)`हो , तो निरोधी विभव (stopping potential ) `v_(0)` के लिए
`E_(k) = (1)/(2)mv_(max)^(2) = eV_(0)` जिसमें `v_(max)` प्रकाश - इलेक्ट्रॉनों की अधिकतम चाल हैं । जब 400 nm तरंगदैर्घ्य वाला बैंगनी प्रकाश एक प्रकाश - वैद्युत सेल पर गिरता हैं , तो इसके कैथोड़ से इलेक्ट्रॉन की गति रोकने के लिए `0.5 eV` के निरोधी विभव की आवश्यकता होती हैं । यदि h `= 6.6 xx 10^(-34)` Js हो , तो
इस सेल के लिए देहली आवृत्ति हैं05:10View Solutionन्यूट्रॉन एक अनावेशित परंतु `9.66xx10^(-27) Am^(2)` का z - अक्षीय चुंबकीय आघूर्ण (magnetic moment) रखनेवाला कण हैं । इसे न्यूट्रॉन के आंतरिक बनावट से समझा जा सकता हैं । प्रायोगिक सत्यापन से यह ज्ञात हुआ हैं कि एक न्यूट्रॉन तीन मूलभूत क्वार्क एक `+(2)/(3)e` आवेश के अप - क्वार्क (u) तथा दो ` - (1)/(3) e` आवेश के डाउन - क्वार्क (d) से मिलकर बना हैं । तीनों क्वार्कों का युग्म इसे अनावेशित बनाता हैं । यदि ये क्वार्क गित में हो , तो एक चुंबकीय आघूर्ण उत्पन्न करते हैं । इस साधारण संरचना में यदि यह माना जाए कि u - क्वार्क घड़ी की दिशा की विपरीत दिशा में जबकि d - क्वार्क घड़ी की दिशा से r त्रिज्या वाले वृत्तीय पथ पर एक समरुप चाल v से चलते हैं , तो निम्नलिखित प्रश्नों के उत्तर दें ।

u - क्वार्क के घूमने के कारण उत्पन्न विद्युत -धारा का मान होगा05:39View Solutionन्यूट्रॉन एक अनावेशित परंतु `9.66xx10^(-27) Am^(2)` का z - अक्षीय चुंबकीय आघूर्ण (magnetic moment) रखनेवाला कण हैं । इसे न्यूट्रॉन के आंतरिक बनावट से समझा जा सकता हैं । प्रायोगिक सत्यापन से यह ज्ञात हुआ हैं कि एक न्यूट्रॉन तीन मूलभूत क्वार्क एक `+(2)/(3)e` आवेश के अप - क्वार्क (u) तथा दो ` - (1)/(3) e` आवेश के डाउन - क्वार्क (d) से मिलकर बना हैं । तीनों क्वार्कों का युग्म इसे अनावेशित बनाता हैं । यदि ये क्वार्क गित में हो , तो एक चुंबकीय आघूर्ण उत्पन्न करते हैं । इस साधारण संरचना में यदि यह माना जाए कि u - क्वार्क घड़ी की दिशा की विपरीत दिशा में जबकि d - क्वार्क घड़ी की दिशा से r त्रिज्या वाले वृत्तीय पथ पर एक समरुप चाल v से चलते हैं , तो निम्नलिखित प्रश्नों के उत्तर दें ।

तीनों क्वार्क युग्म के संयुक्त प्रभाव व्दारा उत्पन्न चुंबकीय आघूर्ण का मान होगा05:39View Solutionन्यूट्रॉन एक अनावेशित परंतु `9.66xx10^(-27) Am^(2)` का z - अक्षीय चुंबकीय आघूर्ण (magnetic moment) रखनेवाला कण हैं । इसे न्यूट्रॉन के आंतरिक बनावट से समझा जा सकता हैं । प्रायोगिक सत्यापन से यह ज्ञात हुआ हैं कि एक न्यूट्रॉन तीन मूलभूत क्वार्क एक `+(2)/(3)e` आवेश के अप - क्वार्क (u) तथा दो ` - (1)/(3) e` आवेश के डाउन - क्वार्क (d) से मिलकर बना हैं । तीनों क्वार्कों का युग्म इसे अनावेशित बनाता हैं । यदि ये क्वार्क गित में हो , तो एक चुंबकीय आघूर्ण उत्पन्न करते हैं । इस साधारण संरचना में यदि यह माना जाए कि u - क्वार्क घड़ी की दिशा की विपरीत दिशा में जबकि d - क्वार्क घड़ी की दिशा से r त्रिज्या वाले वृत्तीय पथ पर एक समरुप चाल v से चलते हैं , तो निम्नलिखित प्रश्नों के उत्तर दें ।

अगर सभी क्वार्क एक ही दिशा में घूमने लगे , तो न्यूट्रॉन का चुंबकीय आघूर्ण होगा05:39View Solutionपृथ्वी की सतहरो अनुरेख गमन करनेवाली रेडियो तरंगो को , जो ट्रांसमीटर ऐंटेना से अभिग्राही ऐंटेना तक पहुँचाती हैं , भू - तरंगे ( ground waves ) कहा जाता हैं । भू - तरंगो व्दारा संकेत के संचरण को भू - तरंग संचार ( ground - wave communication ) कहा जाता हैं । संचरण के क्रम में भू - तरंगों की तीव्रता ( intensity ) में ह्रास होता हैं । यही कारण हैं कि अधिक दूरी के लिए संचार व्यवस्था में भू - तरंगे उपयुक्त नही होती हैं । केवल स्थानीय प्रसारण ( local broadcasting ) मे ही भू - तरंगो का उपयोग किया जाता हैं ।
भू - तरंगो के संचरण में सिग्नल की तीव्रता से ह्रास होने का कारण हैं04:09View Solutionपृथ्वी की सतहों के अनुरेख गमन करने वाली रेडियो तरंगो को , जो ट्रांसमीटर ऐंटेना से अभिग्राही ऐंटेना तक पहुँचाती हैं , भू - तरंगे ( ground waves ) कहा जाता हैं । भू - तरंगो व्दारा संकेत के संचरण को भू - तरंग संचार ( ground - wave communication ) कहा जाता हैं । संचरण के क्रम में भू - तरंगों की तीव्रता ( intensity ) में ह्रास होता हैं । यही कारण हैं कि अधिक दूरी के लिए संचार व्यवस्था में भू - तरंगे उपयुक्त नही होती हैं । केवल स्थानीय प्रसारण ( local broadcasting ) मे ही भू - तरंगो का उपयोग किया जाता हैं ।
आवृत्ति के किस परास (range) के लिए भू - तरंग संचार उपयुक्त होता हैं ?03:41View Solutionकिसी ट्रांसमीटर ऐंटेना से आकाश की ओर प्रेषित रेडियो तरंगो का आयनमंडल से परावर्तन होना और पुनः अभिग्राही ऐंटेना व्दारा प्राप्त होने की प्रक्रिया को आकाश तरंग संचार कहा जाता हैं । ऐसी रेडियो - तरंगो को आकाश तरंग भी कहा जाता हैं । आयनमंडल ( ionosphere) का अस्तित्व पृथ्वी - पृष्ठ से 80 km की ऊँचाई से लेकर 300 km तक होता हैं जो इलेक्ट्रॉन तथा आयन जैसे आवेशित कणों से मिलकर बनता हैं । पृथ्वी की सतह के निकट आयनमंडलीय सतह पर आयनीकरण की डिग्री ( degree of ionization ) अधिक होती हैं और ऊपरी पृष्ठ पर अपेक्षाकृत कम होती हैं । यही कारण है कि आयनमंडल की निचली सतह पर रेडियो - तरंगो का अपवर्तनांक अधिक होता हैं और ऊपर जाने के क्रम में इसका मान घटता जाता हैं ।
आयनमंडल की गैसों का आयनीकरण जिसके व्दारा होता हैं , वह हैं04:08View Solutionकिसी ट्रांसमीटर ऐंटेना से आकाश की ओर प्रेषित रेडियो तरंगो का आयनमंडल से परावर्तन होना और पुनः अभिग्राही ऐंटेना व्दारा प्राप्त होने की प्रक्रिया को आकाश तरंग संचार कहा जाता हैं । ऐसी रेडियो - तरंगो को आकाश तरंग भी कहा जाता हैं । आयनमंडल ( ionosphere) का अस्तित्व पृथ्वी - पृष्ठ से 80 km की ऊँचाई से लेकर 300 km तक होता हैं जो इलेक्ट्रॉन तथा आयन जैसे आवेशित कणों से मिलकर बनता हैं । पृथ्वी की सतह के निकट आयनमंडलीय सतह पर आयनीकरण की डिग्री ( degree of ionization ) अधिक होती हैं और ऊपरी पृष्ठ पर अपेक्षाकृत कम होती हैं । यही कारण है कि आयनमंडल की निचली सतह पर रेडियो - तरंगो का अपवर्तनांक अधिक होता हैं और ऊपर जाने के क्रम में इसका मान घटता जाता हैं ।
रेडियो - तरंगे के लिए आयनामंडल का अपवर्तनांक04:02View Solutionकिसी ट्रांसमीटर ऐंटेना से आकाश की ओर प्रेषित रेडियो तरंगो का आयनमंडल से परावर्तन होना और पुनः अभिग्राही ऐंटेना व्दारा प्राप्त होने की प्रक्रिया को आकाश तरंग संचार कहा जाता हैं । ऐसी रेडियो - तरंगो को आकाश तरंग भी कहा जाता हैं । आयनमंडल ( ionosphere) का अस्तित्व पृथ्वी - पृष्ठ से 80 km की ऊँचाई से लेकर 300 km तक होता हैं जो इलेक्ट्रॉन तथा आयन जैसे आवेशित कणों से मिलकर बनता हैं । पृथ्वी की सतह के निकट आयनमंडलीय सतह पर आयनीकरण की डिग्री ( degree of ionization ) अधिक होती हैं और ऊपरी पृष्ठ पर अपेक्षाकृत कम होती हैं । यही कारण है कि आयनमंडल की निचली सतह पर रेडियो - तरंगो का अपवर्तनांक अधिक होता हैं और ऊपर जाने के क्रम में इसका मान घटता जाता हैं ।
आकाश - तरंग संचरण के लिए रेडियों - तरंग की आवृत्ति का कौन - सा परास (range) उपयुक्त होता हैं ?06:14View Solutionअंतरिक्ष संचार (space communication ) में रेडियो सिग्नल को किसी एक स्थान के ट्रांसमीटर ऐटेना से अंतरिक्ष (space) में भेजा जाता हैं । प्रेषित तरंगे पृथ्वी के क्षोभमंडल ( troposphere ) से होकर किसी दूसरे स्थान पर लगे अभिग्राही ऐंटेना व्दारा अंतर्रोधित ( intercept ) होती हैं । अंतरिक्ष संचार व्यवस्था में रेडियो संके सरल रैखिक पथ पर ट्रांसमीटर ऐंटेना से सीधे अभिग्राही ऐंटेना तक पहुँचाती हैं । स्पष्टतः अंतरिक्ष , संचार व्यवस्था पृथ्वी की वक्रता ( curvature) के कारण प्रतिबंधित (restricted) होती हैं । इस प्रकार के संचरण को दिष्ट तरंग संचरण ( direct wave propagation ) कहा जाता हैं । यदि ट्रांसमीटर के ऐंटेना की ऊँचाई h हो , तो उस स्थान से प्रसारण की अधिकतम दूरी d के लिए , d = `sqrt(2Rh)` , जहाँ पृथ्वी की त्रिज्या R हैं । स्पष्टतः , ट्रांसमीटर के ऐंटेना की ऊँचाई जितनी अधिक होगी , प्रसारण उतने ही अधिक क्षेत्र में पहुँचेगा ।
संचार की किस विधि (mode) में VHF और UHF सिग्नल उपयुक्त होते हैं ?07:54View Solutionअंतरिक्ष संचार (space communication ) में रेडियो सिग्नल को किसी एक स्थान के ट्रांसमीटर ऐटेना से अंतरिक्ष (space) में भेजा जाता हैं । प्रेषित तरंगे पृथ्वी के क्षोभमंडल ( troposphere ) से होकर किसी दूसरे स्थान पर लगे अभिग्राही ऐंटेना व्दारा अंतर्रोधित ( intercept ) होती हैं । अंतरिक्ष संचार व्यवस्था में रेडियो संके सरल रैखिक पथ पर ट्रांसमीटर ऐंटेना से सीधे अभिग्राही ऐंटेना तक पहुँचाती हैं । स्पष्टतः अंतरिक्ष , संचार व्यवस्था पृथ्वी की वक्रता ( curvature) के कारण प्रतिबंधित (restricted) होती हैं । इस प्रकार के संचरण को दिष्ट तरंग संचरण ( direct wave propagation ) कहा जाता हैं । यदि ट्रांसमीटर के ऐंटेना की ऊँचाई h हो , तो उस स्थान से प्रसारण की अधिकतम दूरी d के लिए , d = `sqrt(2Rh)` , जहाँ पृथ्वी की त्रिज्या R हैं । स्पष्टतः , ट्रांसमीटर के ऐंटेना की ऊँचाई जितनी अधिक होगी , प्रसारण उतने ही अधिक क्षेत्र में पहुँचेगा ।
यदि TV टावर की ऊँचाई 80 m हो , तो वह महत्तम दूरी जहाँ तक TV प्रसारण पहुँचेगा , वह हैं (पृथ्वी की त्रिज्या = 6400 km)05:37View Solutionअंतरिक्ष संचार (space communication ) में रेडियो सिग्नल को किसी एक स्थान के ट्रांसमीटर ऐटेना से अंतरिक्ष (space) में भेजा जाता हैं । प्रेषित तरंगे पृथ्वी के क्षोभमंडल ( troposphere ) से होकर किसी दूसरे स्थान पर लगे अभिग्राही ऐंटेना व्दारा अंतर्रोधित ( intercept ) होती हैं । अंतरिक्ष संचार व्यवस्था में रेडियो संके सरल रैखिक पथ पर ट्रांसमीटर ऐंटेना से सीधे अभिग्राही ऐंटेना तक पहुँचाती हैं । स्पष्टतः अंतरिक्ष , संचार व्यवस्था पृथ्वी की वक्रता ( curvature) के कारण प्रतिबंधित (restricted) होती हैं । इस प्रकार के संचरण को दिष्ट तरंग संचरण ( direct wave propagation ) कहा जाता हैं । यदि ट्रांसमीटर के ऐंटेना की ऊँचाई h हो , तो उस स्थान से प्रसारण की अधिकतम दूरी d के लिए , d = `sqrt(2Rh)` , जहाँ पृथ्वी की त्रिज्या R हैं । स्पष्टतः , ट्रांसमीटर के ऐंटेना की ऊँचाई जितनी अधिक होगी , प्रसारण उतने ही अधिक क्षेत्र में पहुँचेगा ।
यदि TV टावर की ऊँचाई 80 m हैं तथा किसी शहर में आबादी का माध्य - घनत्व 2000 व्यक्ति प्रति वर्ग किलोमीटर हो , तो उपर्युक्त प्रश्न में कितनी आबादी तक प्रसारण पहुँचेगा ?06:48View Solution
बहुवैकल्पिक प्रश्न questions and complete solutions for chapter बोध - संबध्द प्रकार के प्रश्न of BHARATI BHAWAN PHYSICS (HINDI) of Class 12
