Complete Solutions to Linked Comprechension Type of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| CENGAGE NEW | Linked Comprechension Type |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Consider an unknow polynomial which divided by `(x - 3)` and `(x-4)` leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by `(x-3)(x-4)`.
If equations `R(x) = x^(2)+ ax +1` has two distint real roots, then exhaustive values of a are.
View SolutionConsider an unknow polynomial which divided by `(x - 3)` and `(x-4)` leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by `(x-3)(x-4)`.
If equations `R(x) = x^(2)+ ax +1` has two distint real roots, then exhaustive values of a are.
View SolutionIf a polynomial f (x) is divided by ` (x - 3) and (x - 4)` it leaves remainders as 7 and 12 respectively, then find the remainder when f (x) is divided by `(x-3)(x-4)`
View SolutionLet `f(x)=x^(2)+bx+c` and `g(x)=x^(2)+b_(1)x+c_(1)`
Let the real roots of `f(x)=0` be `alpha, beta` and real roots of `g(x)=0` be `alpha +k, beta+k` fro same constant `k`. The least value fo `f(x)` is `-1/4` and least value of `g(x)` occurs at `x=7/2`
The valueof `b_(1)` is
View SolutionLet `f(x)=x^(2)+bx+c` and `g(x)=x^(2)+b_(1)x+c_(1)`
Let the real roots of `f(x)=0` be `alpha, beta` and real roots of `g(x)=0` be `alpha +k, beta+k` fro same constant `k`. The least value fo `f(x)` is `-1/4` and least value of `g(x)` occurs at `x=7/2`
The valueof `b_(1)` is
View SolutionLet `f(x)=x^(2)+bx+c` and `g(x)=x^(2)+b_(1)x+c_(1)`
Let the real roots of `f(x)=0` be `alpha, beta` and real roots of `g(x)=0` be `alpha +k, beta+k` fro same constant `k`. The least value fo `f(x)` is `-1/4` and least value of `g(x)` occurs at `x=7/2`
The valueof `b_(1)` is
View SolutionIn the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaAB` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.
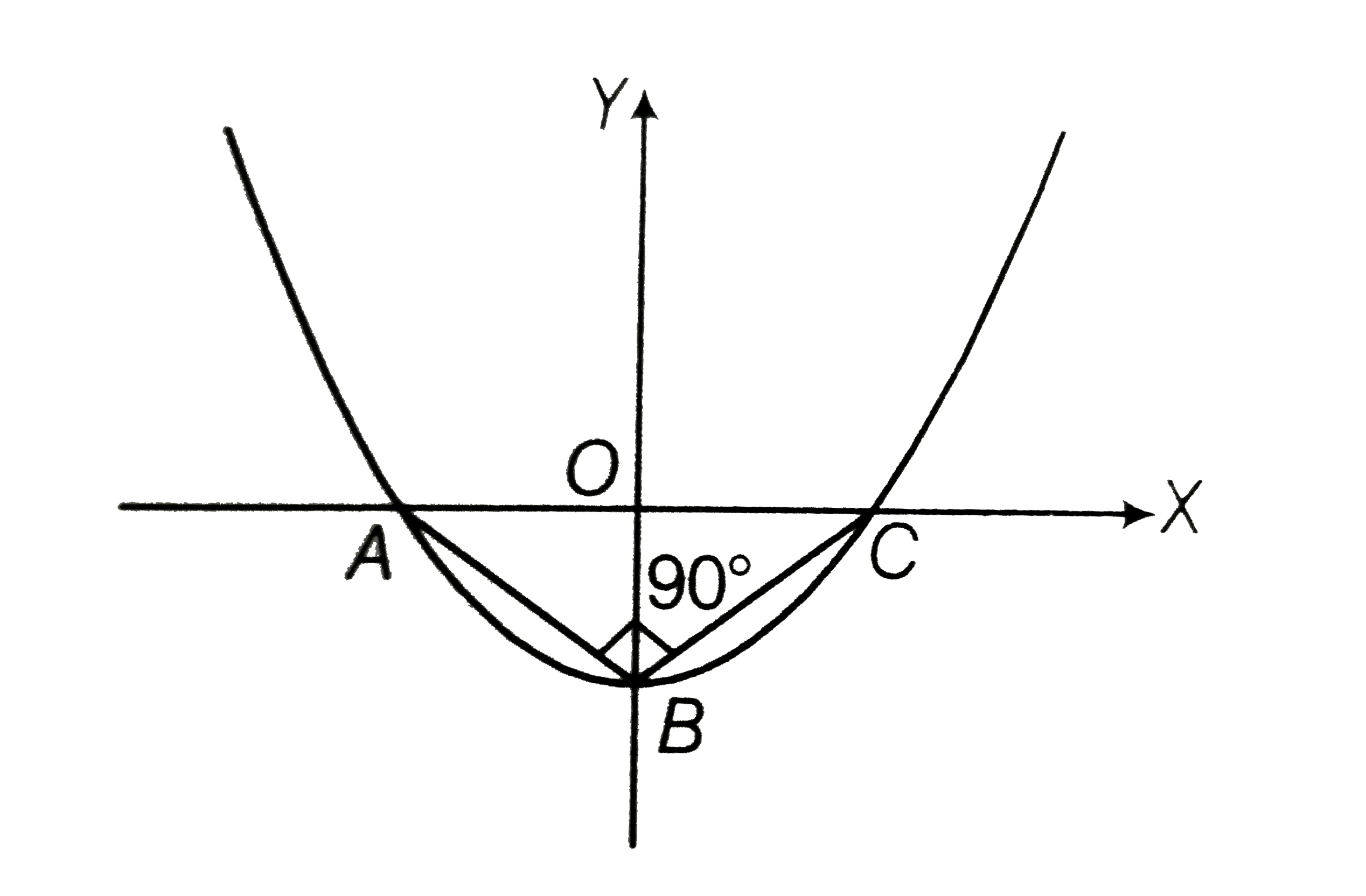
Number of integral value of `lamda` for which `(lamda)/2` lies between the roots of `f(x)=0`, is
View SolutionIn the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaAB` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.

Number of integral value of `lamda` for which `(lamda)/2` lies between the roots of `f(x)=0`, is
View SolutionIn the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaAB` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.

Number of integral value of `lamda` for which `(lamda)/2` lies between the roots of `f(x)=0`, is
View SolutionLet `f(x) =4x^2-4ax+a^2-2a+2` be a quadratic polynomial in `x`,`a` be any real number. If x-coordinate of vertex of parabola y =f(x) is less than 0 and f(x) has minimum value 3 for `x in [0,2]` then value of a is (a) `1+sqrt2` (b) `1-sqrt2` (c) `1-sqrt3` (d) `1+sqrt3`
View SolutionLet `f(x) =4x^2-4ax+a^2-2a+2` be a quadratic polynomial in x,a be any real number. If x-coordinate of the vertex of parabola y =f(x) is less thna 0 and f(x) has minimum value 3 for `x in [0,2]` then value of a is
View SolutionLet `f(x)= 4x^(2) - 4ax + a^(2) - 2a + 2` such that minimum value fo the `f(x)` for `x in [0,2]` is equal to 3.
Number of values of a for which global minimum value, that is equal to 3 for `x in [0,2]`, occurs for the value of x lying in (0,2) is
View SolutionConsdier the equaiton `2 + |x^(2) + 4x + 3_= m , m in R`
Set of all values of m so that the given equaition have two solutions is
View SolutionConsdier the equaiton `2 + |x^(2) + 4x + 3| = m , m in R` Set of all real values of m so that given equation have four distinct solutions, is
View SolutionConsdier the equaiton `2 + |x^(2) + 4x + 3|= m , m in R` Set of all values of m so that the given equaition have two solutions is
View SolutionIf `ax^(2)+bx+c=0` have two distinct roots lying int eh interval `(0,1),a,b,c epislonN`
The least value of `a` is
View SolutionConsider the quadration`ax^(2) - bx + c =0,a,b,c in N` which has two distinct real roots belonging to the interval (1,2).
The least value of b is
View SolutionConsider the quadration`ax^(2) - bx + c =0,a,b,c in N` which has two distinct real roots belonging to the interval (1,2).
The least value of b is
View SolutionConsider the inequation `x^(2) + x + a - 9 < 0`
The values of the real parameter a so that the given inequaiton has at least one positive solution:
View SolutionConsider the inequation `x^(2) + x + a - 9 lt 0`
The values of the real parameter a so that the given inequations has at least one negative solution.
View SolutionConsider the inequation `x^(2) + x + a - 9 lt 0`
The value of the parameter a so that the given inequaiton is ture `AA x in (-1,3)`
View SolutionConsider the inequation `9^(x) -a3^(x) - a+ 3 le 0`, where a is real parameter.
The given inequality has at least one negative solution for `a in ` (a) `(-oo,2)` (b) `(3,oo)` (c) `(-2,oo)` (d) `(2,3)`
View SolutionConsider the inequality `9^(x)-a*3^(x)-a+3le0`, where a is a real parameter.
The given inequality has at least one positive solution for `ain`
View SolutionConsider the inequality `9^(x)-a*3^(x)-a+3le0`, where a is a real parameter.
The given inequality has at least one positive solution for `ain`
View Solution`(af(mu) lt 0)` is the necessary and sufficient condition for a particular real number `mu` to lie between the roots of a quadratic equations `f(x) =0,` where `f(x) = ax^(2) + bx + c`. Again if `f(mu_(1)) f(mu_(2)) lt 0`, then exactly one of the roots will lie between `mu_(1)` and `mu_(2)`.
If `|b| gt |a + c|`, then
View SolutionAn analytic balance has uncertainty in measurement equal to `+- 1 mg`. Then report the result in terms of percentage if the weight of a compound is
a. `1 g` b. `10 g` c. `100 g`
View Solution`(af(mu) lt 0)` is the necessary and sufficient condition for a particular real number `mu` to lie between the roots of a quadratic equations `f(x) =0,` where `f(x) = ax^(2) + bx + c`. Again if `f(mu_(1)) f(mu_(2)) lt 0`, then exactly one of the roots will lie between `mu_(1)` and `mu_(2)`.
If `c(a+b+c) lt 0 lt (a+b+c)a`, then
View SolutionGiven `|px^(2) + qx + r| le |Px^(2) + Qx + R|AA x in R` and `d=q^(2) - 4pr gt 0` and `D =Q^(2) -4PR gt 0`
Which of the following must be ture ?
View SolutionIf `(x+2)` is a common factor of `(px^2+qx+r)` and `(qx^2+px+r)` then (a) ` p=q` or `p+q+r=0` (b)`p=r` or `p+q+r=0` (c) `q=r` or `p+q+r=0` (d)`p=q=-1/2r`
View SolutionConsider the equation `x^(4) + 2ax^(3) + x^(2)+2ax + 1 =0`, where `a in R`.
If exactly two roots are positive and two roots are negative, then the number of intergal values of a is
View SolutionConsider the equation `x^(4) + 2ax^(3) + x^(2)+2ax + 1 =0`, where `a in R`.
If exactly two roots are positive and two roots are negative, then the number of intergal values of a is
View SolutionConsider the equation `x^4 + 2ax^3 + x^2 + 2ax + 1 = 0` where `a in R`. Also range of function `f(x)= x+1/x` is `(-oo,-2]uu[2,oo)` If equation has at least two distinct positive real roots then all possible values of a are
View SolutionThe real numbers `x_1, x_2, x_3` satisfying the equation `x^3-x^2+b x+gamma=0` are in A.P. Find the intervals in which `beta and gamma` lie.
View SolutionThe real numbers `x_1, x_2, x_3` satisfying the equation `x^3-x^2+b x+gamma=0` are in A.P. Find the intervals in which `beta and gamma` lie.
View SolutionIf the equation `x^4- λx^2+9=0` has four real and distinct roots, then `lamda` lies in the interval
View SolutionIf the equation has no real root, then `lamda` lies in the interval
View SolutionIf the equation x^4 -λx^2 +9 has only two real roods, then the set of values of `λ` is
View Solution
Linked Comprechension Type questions and complete solutions for chapter THEORY OF EQUATIONS of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS THEORY OF EQUATIONS
- Archives JEE MAIN (single correct Answer Type )
- Comprehension
- CONCEPT APPLICATION EXERCISE 2.1
- CONCEPT APPLICATION EXERCISE 2.10
- CONCEPT APPLICATION EXERCISE 2.11
- CONCEPT APPLICATION EXERCISE 2.12
- CONCEPT APPLICATION EXERCISE 2.13
- CONCEPT APPLICATION EXERCISE 2.2
- CONCEPT APPLICATION EXERCISE 2.3
- CONCEPT APPLICATION EXERCISE 2.4
- CONCEPT APPLICATION EXERCISE 2.5
- CONCEPT APPLICATION EXERCISE 2.6
- CONCEPT APPLICATION EXERCISE 2.7
- CONCEPT APPLICATION EXERCISE 2.8
- CONCEPT APPLICATION EXERCISE 2.9
- ILLUSTRATION
- JEE ADVANCED (Multiple Correct Answer Type )
- JEE ADVANCED (Numerical Value Type )
- JEE ADVANCED (Multiple Correct Answer Type )
- JEE ADVANCED (Single Correct Type )
- Linked Comprechension Type
- MATRIX MATCH TYPE
- Multiple Correct Answer Type
- Multiple Correct Answer
- NUMERICAL VALUE TYPE
- Single correct Answer
- Single Correct Answer Type : Exercise
- SOLVED EXAMPLES