Complete Solutions to Multiple Correct Answer Type of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| CENGAGE NEW | Multiple Correct Answer Type |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
If `c ne 0` and the equation `(p)/(2x)=(a)/(x+c)+(b)/(x-c)` has two equal roots, then `p` can be
View SolutionIf `alpha,beta` are the roots of the quadratic equation `a x^2+b x+c=0` , then which of the following expression will be the symmetric function of roots a. `|log(alpha/beta)|` b. `alpha^2beta^5+beta^2alpha^5` c. `t a n(alpha-beta)` d. `(log(1/alpha))^2+(logbeta)^2`
View SolutionIf one root of the quadratic equation `px^2 +qx + r = 0 (p != 0)` is a surd `sqrta/(sqrta+sqrt(a-b),` where `p, q, r; a, b` are all rationals then the other root is -
View SolutionIf `a , b ,c` real in G.P., then the roots of the equation `a x^2+b x+c=0` are in the ratio a. `1/2(-1+isqrt(3))` b. `1/2(1-isqrt(3))` `c 1/2(-1-isqrt(3))` d. `1/2(1+isqrt(3))`
View Solutionthe roots of the equation `(a+sqrt(b))^(x^2-15)+(a-sqrt(b))^(x^2-15)=2a` where `a^2-b=1` are
View SolutionIf the equations `x^2+p x+q=0 and x^2+p^(prime)x+q^(prime)=0` have a common root, then it must be equal to a.`(p^(prime)-p ^(prime) q)/(q-q^(prime))` b. `(q-q ')/(p^(prime)-p)` c. `(p^(prime)-p)/(q-q^(prime))` d. `(p q^(prime)-p^(prime) q)/(p-p^(prime))`
View SolutionIf the quadratic equation `a x^2+b x+c=0(a >0)` has `sec^2thetaa n dcos e c^2theta` as its roots, then which of the following must hold good? `b+c=0` b. `b^2-4a cgeq0` c. `ccgeq4a` d. `4a+bgeq0`
View SolutionGiven that `alpha,gamma` are roots of the equation `A x^2-4x+1=0,a n dbeta,delta` the roots of the equation of `B x^2-6x+1=0,` such that `alpha,beta,gamma,a n ddelta` are in H.P., then a.`A=3` b. `A=4` `B=2` d. `B=8`
View SolutionIf `cos^4theta+alpha` are the roots of the equation `x^2+2b x+b=0a n dcos^2theta+beta,sin^2theta+betaa r e` the roots of the equation `x^2+4x+2=0,` then values of `b` are `2` b. `-1` c. `-2` d. `2`
View SolutionIf `alpha,beta` are the roots of the equation `ax^2 + bx+c=0` then the roots of the equation `(a + b + c)x^2-(b + 2c)x+c=0` are (a) `c` (b) `d-c` (c) `2c` (d) 0
View SolutionIf every pair of equations `x^2+ax+bc=0, x^2+bx+ca=0` and `x^2+cx+ab=0` has a common root then their sum is
View SolutionIf the equation `4x^2-x-1=0 and 3x^2+(lambda+mu)x+lambda-mu=0` have a root common, then the irrational values of `lambda and mu` are (a) `lambda=(-3)/4` b. `lambda=0` c. `mu=3/4` b.`mu=0`
View SolutionIf `x^3+3x^2-9x+c` is of the form `(x-alpha)^2(x-beta)` then `c` is equal to
View SolutionIf the equation whose roots are the squares of the roots of the cubic `x^3-a x^2+b x-1=0` is identical with the given cubic equation, then (A) `a=0,b=3` (B) `a=b=0` (C) `a=b=3` (D) `a ,b ,` are roots of`x^2+x+2=0`
View SolutionIf ` f(x) ` is a polynomial of degree 4 with rational coefficients
and touches x - axis at ` (sqrt(2) , 0 )` , then for the equation
` f(x) = 0`,
View Solution`(x^3+1/x^3)+(x^2+1/x^2)-6(x+1/x)-7=0`
View Solution`2x^2+6xy+5y^2=1, then`
View SolutionIf ` f(x) = ax^(2) + bx + c ` , where ` a ne 0, b ,c in ` R , then which of
the following conditions implies that f(x) has real roots?
View SolutionIf `(x^(2) + 5)/(2) = x - 2` cos (m + n)` has at least one real root, the
View SolutionLet three quadratic equations ` ax^(2) - 2bx + c = 0, bx^(2) - 2 cx + a = 0`
and `cx^(2) -2 ax + b = 0 `, all have only positive roots. Then ltbr. Which of these are always ture?
View SolutionFor the quadratic equation `x^2+2(a+1)x+9a-5=0,` which of the following is/are true? (a) If `2 < a < 5` , then roots are opposite sign (b)If `a < 0` , then roots are opposite in sign (c) if `a > 7` then both roots are negative (d) if `2 <= a <= 5` then roots are unreal
View SolutionIf `a ,b ,c in Ra n da b c<0` , then equation `b c x^2+2b+c-a)x+a=0h a s` both positive roots both negative roots real roots one positive and one negative root
View SolutionThe graph of the quadratic trinomial `u=a x^2+b x+c` has its vertex at (4, -5) and two x-intercepts, one positive and one negative. Which of the following holds good? a. `a >0` b. `b<0` c. `c<0` d. `8a=b`
View SolutionLet `a ,b ,c in Q^+` satisfying `a > b > cdot` Which of the following statements (s) hold true of the quadratic polynomial `f(x)=(a+b-2c)x^2+(b+c-2a)x+(c+a-2b)?` The mouth of the parabola `y=f(x)` opens upwards Both roots of the equation `f(x)=0` are rational The x-coordinate of vertex of the graph is positive The product of the roots is always negative
View SolutionLet `f(X) = ax^(2) + bx + c `. Consider the following diagram
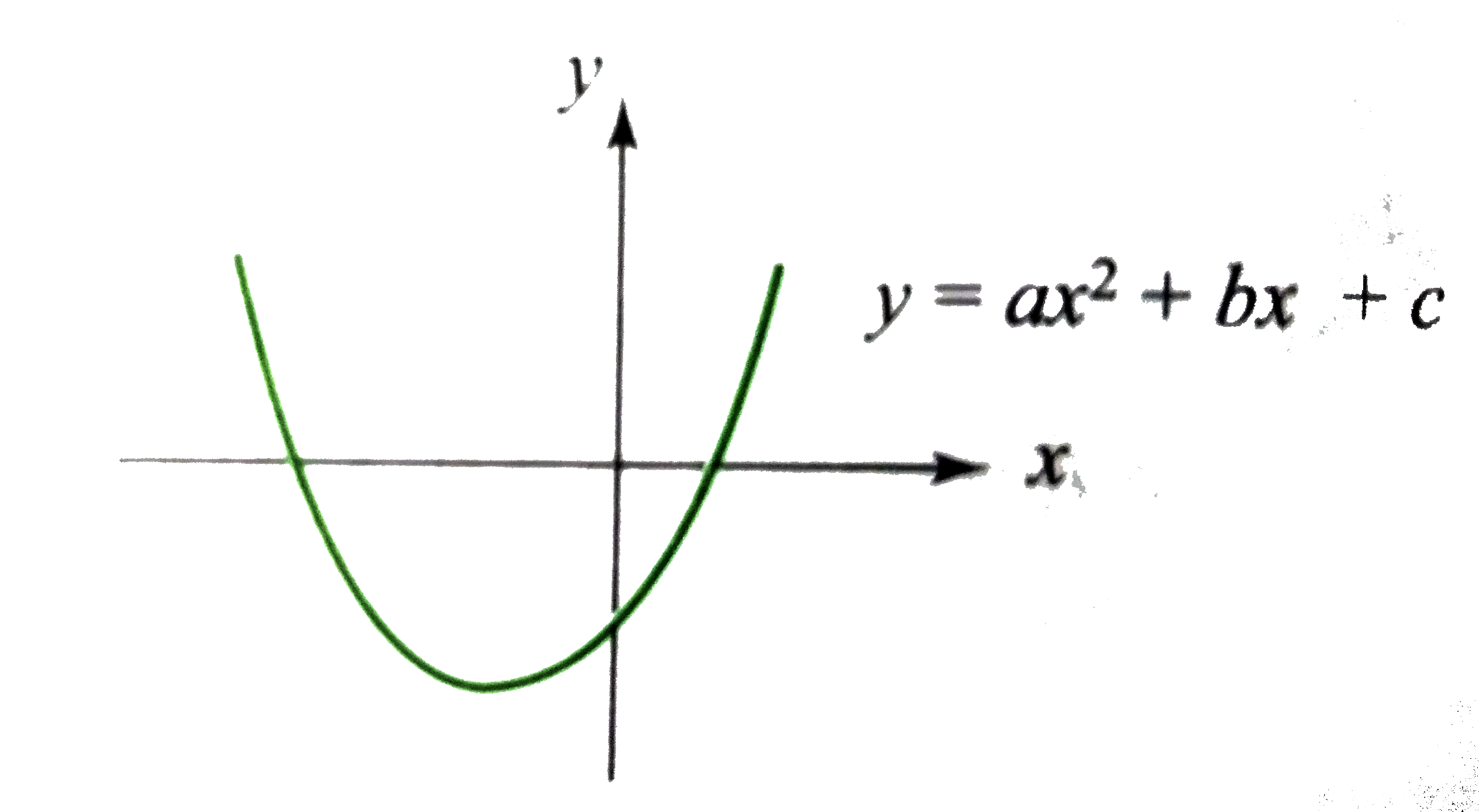 .
.
View SolutionGraph of y = ax^(2) + bx + c is as shown in the figure . If ` PQ= 9,`
`OR = 5` and `OB = 2.5`, the which of the following is /are ture?
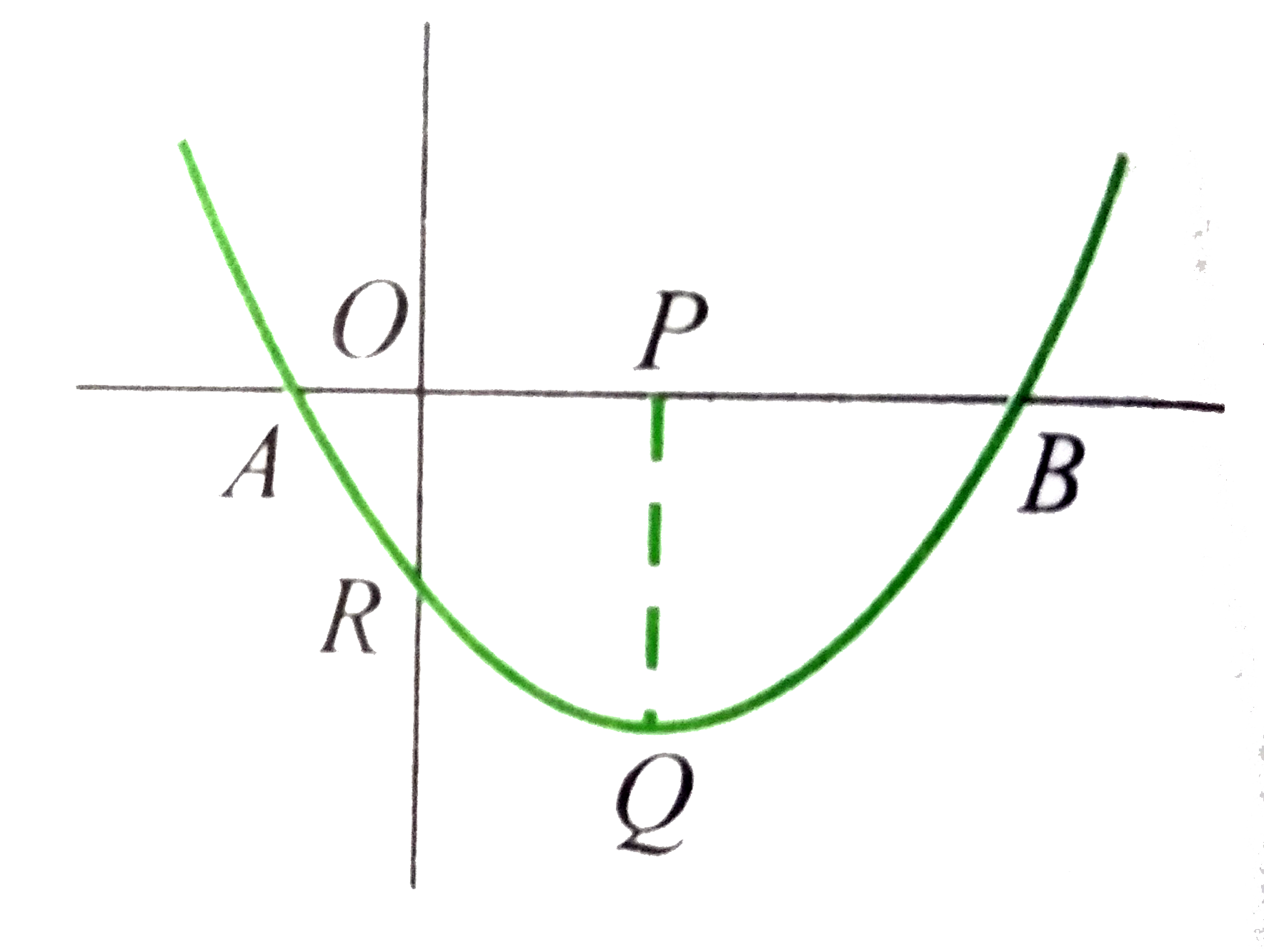
View Solution`ax^2 + bx + c = 0(a > 0),` has two roots `alpha and beta` such `alpha < -2 and beta > 2,` then
View SolutionIf the equation `ax^(2) + bx + c = 0, a,b, c, in` R have non -real
roots, then
View SolutionIf `cos x - y^(2) - sqrt(y - x ^(2) - 1 )ge 0 ` , then
View SolutionIf `ax^(2)+(b-c)x+a-b-c=0` has unequal real roots for all `c epsilonR`, then
View SolutionIf `(x^2+a x+3)/(x^2+x+a)` takes all real values for possible real values of `x ,` then a.`a^3-9a+12<=0` b. `4a^5+39 >=0` c. `ageq1/4` d. `a<1/4`
View SolutionIf the range of function ` f(x) = (x + 1)/(k+x^(2))` contains the interval
[-0,1] , then values of k can be equal to
View SolutionConsider equation `(x - sin alpha) (x-cos alpha) - 2 = 0` . Which of the following is /are true?
View SolutionIf the roots of the equation, `x^3 + px^2+qx-1 = 0` form an increasing` G.P.` where `p` and `q`are real,then (a) `p +q = 0` (b) `p in (-3, oo)` (c) one of the roots is unity (d) one root is smaller than 1 and one root is greater than 1
View SolutionConsider a quadratic equation `ax^2 + bx + c = 0` having roots `alpha, beta`. If `4a + 2b + c > 0,a-b+c < 0 and 4a - 2b + C > 0` then `|[alpha] + [beta]|` can be {where [] is greatest integer}
View SolutionThe equation `(x/(x+1))^2+(x/(x-1))^2=a(a-1)` has
a. Four real roots if `a >2`
b.Four real roots if `a<-1`
c. Two real roots if `1 < a < 2`
d . No real roots if `a<-1`
View Solutionlf the quadratic equations `x^2+bx+c=0` and `bx^2+cx+1=0` have a common root then prove that either `b+c+1=0` or `b^2+c^2+1=bc+b+c`.
View SolutionIf the inequality `cot^(2)x + (k +1) cot x - (k-3) < 0` is true for at least one `x in (0, pi//2)`, then `k in `.
View Solution
Multiple Correct Answer Type questions and complete solutions for chapter THEORY OF EQUATIONS of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS THEORY OF EQUATIONS
- Archives JEE MAIN (single correct Answer Type )
- Comprehension
- CONCEPT APPLICATION EXERCISE 2.1
- CONCEPT APPLICATION EXERCISE 2.10
- CONCEPT APPLICATION EXERCISE 2.11
- CONCEPT APPLICATION EXERCISE 2.12
- CONCEPT APPLICATION EXERCISE 2.13
- CONCEPT APPLICATION EXERCISE 2.2
- CONCEPT APPLICATION EXERCISE 2.3
- CONCEPT APPLICATION EXERCISE 2.4
- CONCEPT APPLICATION EXERCISE 2.5
- CONCEPT APPLICATION EXERCISE 2.6
- CONCEPT APPLICATION EXERCISE 2.7
- CONCEPT APPLICATION EXERCISE 2.8
- CONCEPT APPLICATION EXERCISE 2.9
- ILLUSTRATION
- JEE ADVANCED (Multiple Correct Answer Type )
- JEE ADVANCED (Numerical Value Type )
- JEE ADVANCED (Multiple Correct Answer Type )
- JEE ADVANCED (Single Correct Type )
- Linked Comprechension Type
- MATRIX MATCH TYPE
- Multiple Correct Answer Type
- Multiple Correct Answer
- NUMERICAL VALUE TYPE
- Single correct Answer
- Single Correct Answer Type : Exercise
- SOLVED EXAMPLES