Complete Solutions to Linked comprehension type of chapter PROPERTIES AND SOLUTIONS OF TRIANGLE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES AND SOLUTIONS OF TRIANGLE |
| CENGAGE NEW | Linked comprehension type |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Given that `Delta = 6, r_(1) = 3, r_(3) = 6`
Circumradius R is equal to
View SolutionGiven that `Delta = 6, r_(1) = 3, r_(3) = 6`
Inradius is equal to
View SolutionGiven that `Delta = 6, r_(1) = 2,r_(2)=3, r_(3) = 6` Difference between the greatest and the least angles is
View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Area (in sq. units) of the triangle is equal to
View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Angle C is equal to
View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Value of `sin A` is equal to
View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.BH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of `(cos A. cos B . cos C)/(cos^(2)A + cos^(2)B + cos^(2)C)` is
View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.BH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of R is
View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.BH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of `HD.HE.HF` is
View SolutionLet `O` be a point inside a triangle `A B C` such that `/_O A B=/_O B C=/_O C A=omega` , then show that: `cotomega=cotA+cotB+cot C` `Cos e c^2omega=cos e c^2A+cos e c^2B+cos e c^2C`
View Solutionfind the principle value of `cos^(-1)((sqrt3)/2)`
View SolutionLet O be a point inside `DeltaABC` such that
`angleAOB = angleBOC = angle COA = theta`
Area of `DeltaABC` is equal to
View SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the circumradius R is given by
View SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the inradius r is given by
View SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the distance between circumcenter O and incenter I is
View SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
`angleDEF` is equal to
View SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
`angleDEF` is equal to
View SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
The length of side EF is
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A`,`90^@-1/2B` and `90^@-1/2C`
View SolutionInternal bisectors of `DeltaABC` meet the circumcircle at point D, E, and F
Area of `DeltaDEF` is
View SolutionInternal bisectors of `DeltaABC` meet the circumcircle at point D, E, and F
Area of `DeltaDEF` is
View SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minimum value of the sum of the lenghts of diagonals is
View SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The sides of the triangle are in the ratio
View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The value of `R : r` is
View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The greatest angle of the triangle is given by
View SolutionIn `DeltaABC, P,Q, R` are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. `DeltaPQR` is constructed

If `angleBAC = 120^(@)`, then measusred of `angleRPQ` will be
View SolutionIn `triangleABC, P,Q, R` are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. `trianglePQR` is constructed
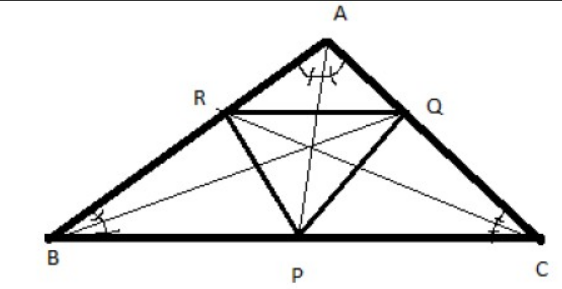
If `AB = 7` units, BC = 8 units, AC = 5 units, then the side PQ will be
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If `BC = 6, AC = 8`, then the length of side AB is equal to
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A `
`If `angleGAC = (pi)/(3) and a = 3b`, then sin C is equal to
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal to
View SolutionThe inradius in a right angled triangle with integer sides is r
If r = 4, the greatest perimeter (in units) is
View SolutionThe inradius in a right angled triangle with integer sides is r
If r = 5, the greatest area (in sq. units) is
View Solution
Linked comprehension type questions and complete solutions for chapter PROPERTIES AND SOLUTIONS OF TRIANGLE of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS PROPERTIES AND SOLUTIONS OF TRIANGLE
- Archives (JEE Advanced)
- Archives (Matrix Match Type)
- Archives (Multiple correct Answer Type)
- Archives (Numerical Value Type)
- Archives (Single correct Answer type)
- Concept application exercise 5.1
- Concept application exercise 5.10
- Concept application exercise 5.11
- Concept application exercise 5.2
- Concept application exercise 5.3
- Concept application exercise 5.4
- Concept application exercise 5.5
- Concept application exercise 5.6
- Concept application exercise 5.7
- Concept application exercise 5.8
- Concept application exercise 5.9
- example
- Exercises
- Illustration
- Linked comprehension type
- Matrix match type
- Multiple correct answer type
- Numerical value type