Complete Solutions to Examples of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| CENGAGE NEW | Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let f(x) be a quadratic polynomial satisfying f(2) + f(4) = 0.
If unity is one root of f(x) = 0 then find the other root.02:49View SolutionA polynomial in `x` of degree 3 vanishes when `x=1` and `x=-2` , ad has the values 4 and 28 when `x=-1` and `x=2` , respectively. Then find the value of polynomial when `x=0` .
03:37View SolutionLet `f(x)=A x^2+B x+c ,w h e r eA ,B ,C` are real numbers. Prove that if `f(x)` is an integer whenever `x` is an integer, then the numbers `2A ,A+B ,a n dC` are all integer. Conversely, prove that if the number `2A ,A+B ,a n dC` are all integers, then `f(x)` is an integer whenever `x` is integer.
05:34View SolutionProve that
`(ax^(2))/((x -a)(x-b)(x-c))+(bx)/((x -b)(x-c))+(c)/(x-c)+1`
`= (x^(3))/((x-a)(x-b)(x-c))`.View SolutionFind the remainder when `x^3+4x^2-7x+6` is divided by `x-1.`
02:34View SolutionIf the expression `a x^4+b x^3-x^2+2x+3` has remainder `4x+3` when divided by `x^2+x-2,` find the value of `aa n dbdot`
03:33View SolutionLet `a!=0a n dp(x)` be a polynomial of degree greater than 2. If `p(x)` leaves reminders `aa n d a` when divided respectively, by `+aa n dx-a ,` the remainder when `p(x)` is divided by `x^2-a^2` is `2x` b. `-2x` c. `x` d. ` x`
05:21View SolutionGiven that `x^2+x-6` is a factor of `2x^4+x^3+b x+a+b-1,` find the value of `aa n dbdot`
03:02View SolutionUse the factor theorem to find the value of `k` for which `(a+2b),w h e r ea ,b!=0` is a factor of `a^4+32 b^4+a ^3b(k+3)dot`
02:54View SolutionIf `c ,d` are the roots of the equation `(x-a)(x-b)-k=0` , prove that a, b are roots of the equation `(x-c)(x-d)+k=0.`
01:45View SolutionLet `f(x)= x^(3) + x + 1` and P(x) be a cubic polynomial such that P(0) = -1 and roots of f(0) = 1 ; P(x) = 0 are the squares of the roots of f(x) = 0 . Then find the value of P(4).
View SolutionLet f(x) be a polynomial with integral coefficients. If f(1) and f(2) both are odd integers, prove that f(x) = 0 can' t have any integral root.
03:24View SolutionLet `a ,b in na n a > 1.` Also `p` is a prime number. If `a x^2+b x+c=p` for any intergral values of `x ,` then prove that `a+b x+c!=2p` for any integral value of `xdot`
03:20View SolutionWhat is Identity equation & Inequalities ? (i)If `(a^2-1)x^2+(a-1)x+a^2-4a+3=0` is an identity in x; then find the value of a .
02:07View SolutionShow that `((x+b)(x+c))/((b-a)(c-a))+((x+c)(x+a))/((c-b)(a-b))+((x+a)(x+b))/((a-c)(b-c))=1` is an identity.
05:17View SolutionA certain polynomial `P(x)x in R` when divided by k`x-a ,x-ba n dx-c` leaves remainders`a , b ,a n dc` , resepectively. Then find remainder when `P(x)` is divided by `(x-a)(x-b)(x-c)w h e r eab, c` are distinct.
06:06View SolutionIf `alpha,beta,gamma` are such that `alpha+beta+gamma=2,""alpha^2+beta^2+gamma^2=6,""alpha^3+beta^3+gamma^3=8,t h e n""alpha^4+beta^4+gamma^4` is a. 18 b. 10 c. 15 d. 36
03:41View SolutionIf `x + y + z = 12, x^(2) + Y^(2) + z^(2) = 96` and `(1)/(x)+(1)/(y)+(1)/(z)= 36` . Then find the value `x^(3) + y^(3)+z^(3).`
05:04View SolutionIn how many points graph of `y=x^3-3x2+5x-3` interest the x-axis?
02:42View SolutionConsider the following figure.
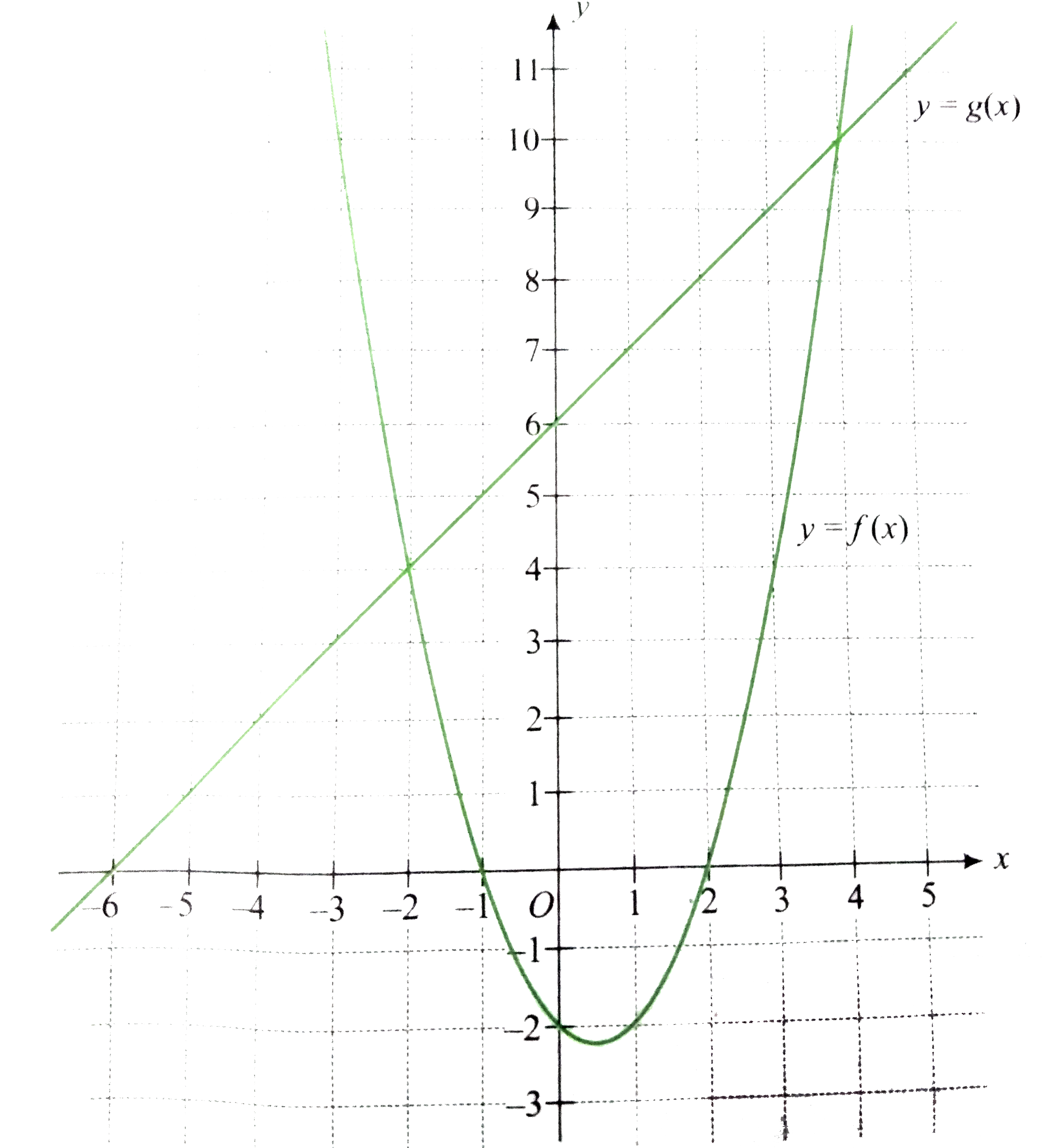
Answer the following questions
(i) What are the roots of the f(x) = 0?
(ii) What are the roots of the f(x) = 4?
(iii)What are the roots of the f(x) = g (x)?02:14View SolutionWhich of the following pair of graphs intersect ?
(i) y = `x^(2) - x ` and y = 1
(ii) y = `x^(2) - 2x + 3` and y = sin x
(iii) = `x^(2) - x + 1` and y = x - 4View SolutionSolve `(x^2-2x-3)/(x+1)=0.`
01:39View SolutionSolve `(x^3-4x)sqrt(x^2-1)=0.`
02:23View SolutionSolve `(2x-3)/(x-1)+1=(6x-x^2-6)/(x-1)dot`
02:43View SolutionEvaluate `x=sqrt(6+sqrt(6+sqrt(6+.....oodot)))`
01:29View SolutionAnalyze the roots of the following equations:
(i) `2x^(3) - 9x^(2) + 12x - (9//2) = 0`
(ii) `2x^(3) - 9x^(2) + 12x - 3 = 0`06:47View SolutionFind how many roots of the equations `x^4+2x^2-8x+3=0.`
03:33View SolutionHow many real solutions does the equation `x^7+14 x^5+16 x^3+30 x-560=0` have?
02:42View SolutionSolve `sqrt(5x^2-6x+8)+sqrt(5x^2-6x-7)=1.`
View SolutionSolve `(x^2-5x+7)^2-(x-2)(x-3)=1.`
03:57View SolutionSolve the equation `4^(x)- 5 xx2^(x) + 4 = 0.`
03:01View SolutionSolve the equation `12^x-56 x^2+89 x^2-56 x+12=0.`
View SolutionSolve the equation `3x^(2-x)+4x^(2-x)=25.`
View SolutionSolve the equation `(x-1)^4+(x-5)^4=82.`
View SolutionSolve the equation `(x+2)(x+3)(x+8)xx(x+12)=4x^2dot`
View SolutionIf the roots of the equation `x^2-8x+a^2-6a=0` are real distinct, then find all possible value of `adot`
View SolutionIf the roots of the equation `a(b-c)x^2+b(c-a)x+c(a-b)=0` are equal, show that `2//b=1//a+1//cdot`
View SolutionProve that the roots of the equation `(a^4+b^4)x^2+4a b c dx+(c^4+d^4)=0` cannot be different, if real.
View SolutionIf roots of equation `x^3-2c x+a b=0` are real and unequal, then prove that the roots of `x^2-2(a+b)x+a^2+b^2+2c^2=0` will be imaginary.
View SolutionFind the quadratic equation with rational coefficients whose one root is `1//(2+sqrt(5))dot`
View SolutionIf `f(x)=a x^2+b x+c ,g(x)=-a x^2+b x+c ,w h e r ea c!=0,` then prove that `f(x)g(x)=0` has at least two real roots.
02:37View SolutionIf `a ,b ,c` are non zero`(a b c^2)x^2+3a^2c x+b^2c x-6a^2-a b+2b^2=0` are rational.
04:15View SolutionIf `a gt 0 and b^(2) - 4 ac = 0` then solve `ax^(3) + (a + b) x^(2) + (b + c) x + c gt 0` .
02:35View SolutionIf `a ,b ,a n dc` are odd integers, then prove that roots of `a x^2+b x+c=0` cannot be rational.
View SolutionIf `aa n dc` are odd prime numbers and `a x 62+b x+c=0` has rational roots , where `b in I ,` prove that one root of the equation will be independent of `a ,b ,cdot`
10:09View SolutionFind the range of the fuction f(x) = x^(2) - 2x -4`
View SolutionFind the least value of `((6x^2-22 x+21))/((5x^2-18+17))` for real `xdot`
View SolutionProve that if the equation `x^2+9y^2-4x+3=0` is satisfied for real values of `xa n dy ,t h e nx` must lie between 1 and 3 and`y` must lie between-1/3 and 1/3.
04:17View SolutionThe least value of the expression `x^2+4y^2+3z^2-2x-12 y-6z+14` is a.`3` b. no least value`` c. `0` d. none of these
04:31View SolutionFind he linear factors of `2x^2-y^2-x+x y+2y-1.`
View SolutionFind the values of `m` for which the expression `2x^2+m x y+3y^2-5y-2` can be resolved into two rational linear factors.
04:49View SolutionForm a quadratic equation whose roots are `-4a n d6.`
View SolutionForm a quadratic equation with real coefficients whose one root is `3-2idot`
View SolutionIf roots of the equation `a x^2+b x+c=0` are `alphaa n dbeta` , find the equation whose roots are `1/alpha,1/beta` (ii) `alpha,-beta` (iii) `(1-alpha)/(1+alpha),(1-beta)/(1+beta)`
View SolutionIf `alpha,beta` are the roots of lthe equation `2x 62-3x-6=0,` find the equation whose roots are `alpha^2+2a n dbeta^2+2.`
View SolutionIf `alpha!=betaa n dalpha^2=5alpha-3a n dbeta^2=5beta-3.` find the equation whose roots are `alpha//betaa n dbeta//alphadot`
View SolutionIf roots of equation `3x^(2) + 5x + 1 = 0` are `(sectheta_(1) - tentheta_(1)) and (cosectheta_(2)-cottheta_(2)),` then find the equation whose roots are `(sectheta_(1)+tantheta_(1) and (cosectheta_(2) + cottheta_(2)).`
03:48View SolutionIf `a b+b c+c a=0,` then solve `a(b-2c)x^2+b(c-2a)x+c(a-2b)=0.`
View SolutionIf `a ,b ,a n dc` are in A.P. and one root of the equation `a x^2+b c+c=0i s2,` the find the other root`dot`
View SolutionIf `alpha` is a root of the equation `4x^2+2x-1=0,` then prove that `4alpha^3-3alpha` is the other root.
05:20View SolutionIf the roots of the equadratic equation `x^(2) + px + q = 0 " are " tan23^(@) "and" tan22^(@),` then find the value of q - p .
02:50View SolutionThe sum of roots of equation `1/(x+a)+1/(x+b)=1/c` is zero find the product of roots of equation a)0 b) `((a+b)/2)` c)`-((a^2+b^2)/2)` d) `2(a^2+b^2)`
View SolutionSolve the equation `x^2+p x+45=0.` it is given that the squared difference of its roots is equal to 144
04:21View SolutionIf `alpha,beta` are the roots of the equation `2x^2-35x+2=0` , the find the value of `(2alpha-35)^3(2beta-35)^3dot`
03:31View SolutionFind a quadratic equation whose product of roots `x_1a n dx_2` is equal to 4 an satisfying the relation `(x_1)/(x_1-1)+(x_2)/(x_2-1)2.`
View SolutionIf `alpha,beta` are roots of `x^2+-p x+1=0a n dgamma,delta` are the roots of `x^2+q x+1=0` , then prove that `q^2-p^2=(alpha-gamma)(beta-gamma)(alpha+delta)(beta+delta)` .
View SolutionIf p and q are the roots of the equation `x^(2)+px+q=0`, then
02:29View SolutionLet n `in` Z and `DeltaABC` be a right tirangle with angle at C . If sin A and sin B are the roots of the equadratic equation `(5n + 8) x^(2) - (7n - 20) x + 120 = 0` , then find the value of n.
03:50View SolutionFind the value of `a` for which one root of the quadratic equation `(a^2-5a+3)x^2+(3a-1)x+2=0` is twice as large as the other.
View SolutionFind t values of the parameter `a` such that the rots `alpha,beta` of the equation `2x^2+6x+a=0` satisfy the inequality `alpha//beta+beta//alpha<2.`
View SolutionLet a, b, c be real numbers with a = 0 and let `alpha,beta ` be the roots of the equation `ax^2 + bx + C = 0`. Express the roots of `a^3x^2 + abcx + c^3 = 0` in terms of `alpha,beta`
02:53View SolutionLet `alpha and beta` be the roots of `x^2 - 5x - 1 = 0` then the value of `(alpha^15 + alpha^11 + beta^15 + beta^11)/(alpha^13 + beta^13)` is
04:56View SolutionIf `alpha,beta` are the roots of the equation `a x^2+b x+c=0,` then find the roots of the equation `a x^2-b x(x-1)+c(x-a)^2=0` in term of `alphaa n dbetadot`
07:45View SolutionIf `alpha and beta` are roots of the equatioin `a cos theta + b sin theta = c`, then find the value of `tan (alpha + beta).`
05:19View SolutionDetermine the values o `m` for which equations `3x^2+4m x+2=0a n d2x^2+3x-2=0` may have a common root.
View SolutionIf `x^2+p x+q=0a n dx^2+q x+p=0,(p!=q)` have a common roots, show that `1+p+q=0` . Also, show that their other roots are the roots of the equation `x^2+x+p q=0.`
03:35View SolutionIf equations `x^2+a x+12=0. x^2+b x+15=0a n dx^2+(a+b)x+36=0,` have a common positive root, then find the values of `aa n dbdot`
View SolutionThe equations `x^2 +3x+5=0 `and `ax^2+bx+c=0` have a common root. If `a,b,c in N` then the least possible values of a+b+c is equal to
03:16View SolutionIf `a ,b ,p ,q` are nonzero real numbers, then how many oon roots would two equations `2a^2x^2-2a b x+b^2=0a n dp^2x^2+2p q x+q^2=0` have?
View Solution`a ,b ,c` are positive real numbers forming a G.P. ILf `a x 62+2b x+c=0a n ddx^2+2e x+f=0` have a common root, then prove that `d//a ,e//b ,f//c` are in A.P.
View SolutionFind the condition on `a , b ,c ,d` such that equations `2a x^2+b^2+c x+d=0a n d2a x 62+3b x+4x=0` have a common root.
View SolutionNumber of positive integers `x` for which `f(x)=x^3-8x^2+20 x-13` is a prime number is______.
View SolutionIf r is positive real number such that `4sqrt(r)-(1)/(4sqrt(r))= 4,` then find the value of ` 6sqrt(r)+(1)/(6sqrt(r)).`
View SolutionIf `alpha, beta and gamma` the roots of the equation `x^(3) + 3x^(2) - 4x - 2 = 0.`
then find the values of the following expressions:
(i) `alpha ^(2) + beta^(2) + gamma^(2)`
(ii)`alpha ^(3) + beta^(3) + gamma^(3)`
(iii) `(1)/(alpha)+(1)/(beta)+(1)/(gamma)`05:16View SolutionIf `alpha,beta,gamma` are the roots of the equation `x^3 + 4x +1=0` then `(alpha+beta)^(-1)+(beta+gamma)^(-1)+(gamma+alpha)^(-1)=`
03:17View SolutionEquations `x^3+5x 62+p x+q=0a n dx 63+7x^2+p x+r=0` have two roots in common. If the third root of each equation is `x_1a n dx_2` , respectively, then find the ordered pair `(x_1, x_2^)dot`
02:20View SolutionIf `alpha, beta and gamma` are the roots of the equation `x^(3) + 3x^(2) - 24x + 1 = 0`
thebn find the value of `(3sqrt(alpha)+3sqrt(beta)+ 3sqrt(gamma)).`04:17View SolutionIf euation `x^(3) + ax^(2) + bx + c = 0,` where a, b, c `in Q (a ne `1). If the real roots of the equation are `x_(1), x_(2) and x_(1)x_(2),` then prove that `x_(1)x_(2)` is rational.
View SolutionSolve the equation `x^3-13 x^2+15 x+189=0` if one root exceeds the other by 2.
View SolutionIn equation `x^4-2x^3+4x^2+6x-21=0` if two of its roots are equal in magnitude but opposite in sign find the roots.
04:01View SolutionIf `b^2<2a c` , then prove that `a x^2+b x^2+c x+d=0` has exactly one real root.
View SolutionIf `f(x)=x^3+b x^2+c x+da n df(0),f(-1)` are odd integers, prove that `f(x)=0` cannot have all integral roots.
05:02View SolutionIf `x-c` is a factor of order m of the polynomial `f(x)` of degree n `(1 < m < n)`, then find the polynomials for which `x=c` is a root.
03:40View SolutionWhat is the minimum height of any point on the curve `y=x^2-4x+6` above the x-axis?
View SolutionWhat is the minimum height of any point on the curve `y=x^2+6x-5` above the x-axisdv?
View SolutionFind the largest natural number a for which the maximum value of `f(x)=a-1+2x-x^2` is smaller thante ninimum value of `g(x)=x^2-2a x=10-2adot`
View SolutionLet `f(x)=a x^2+b x+c` be a quadratic expression having its vertex at (3, -2) and value of `f(0)=10. F in df(x)dot`
View SolutionFind the least value of `n` such that `(n-2)x^2+8x+n+4>0,AAx in R ,w h e r en in Ndot`
View SolutionGiven that `a ,b ,c` are distinct real numbers such that expressions `a x^2+b x+c ,b x^2+c x+aa n dc x^2+a x+b` are always non-negative. Prove that the quantity `(a^2+b^2+c^2)//(a b+b c+c a)` can never lie inn `(-oo,1) ∪ [ 4 , ∞ ) .` .
View SolutionFor a `in` R, if `|x - a + 3| + |x-3a|=2x - 4a +3 |` is ture `AA x in`R. Then find the value of a.
02:46View Solution
Examples questions and complete solutions for chapter THEORY OF EQUATIONS of CENGAGE of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS THEORY OF EQUATIONS
- Comprehension
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 2.1
- Exercise 2.10
- Exercise 2.11
- Exercise 2.12
- Exercise 2.13
- Exercise 2.2
- Exercise 2.3
- Exercise 2.4
- Exercise 2.5
- Exercise 2.6
- Exercise 2.7
- Exercise 2.8
- Exercise 2.9
- JEE Advanced Previous Year
- JEE Main Previous Year
- Multiple Correct Answer
- Single correct Answer
