Complete Solutions to Single correct Answer of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| CENGAGE NEW DPP | Single correct Answer |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
Number of real solutions of `sqrt(2x-4)-sqrt(x+5)=1` is
13:00View SolutionNumber of real solutions of `sqrt(x)+sqrt(x-sqrt(1-x))=1` is
13:29View SolutionThe set of real values of `a` for which the equation `(2a^(2)+x^(2))/(a^(3)-x^(3))-(2x)/(ax+a^(2)+x^(2))+(1)/(x-1)=0` has a unique solution is
08:35View SolutionNumber of distinct real solutions of the equation `x^(2)+((x)/(x-1))^(2)=8` is
14:59View SolutionIf `m`, `n` are positive integers and `m+nsqrt(2)=sqrt(41+24sqrt(2))`, then `(m+n)` is equal to
13:03View SolutionThe equation `(x+3-4(x-1)^(1//2))^(1//2)+(x+8-6(x-1)^(1//2))^(1//2)=1` has (A) no solution (B) only `1` solution (C) only `2` solutions (D) more than `2` solutions
02:40View SolutionThe number of solutions of `sqrt(3x^(2)+x+5)=x-3` is (A) `0` (B) `1` (C) `2` (D) `4`
06:39View SolutionThe number of real or complex solutions of `x^(2)-6|x|+8=0` is
05:56View SolutionIf `alpha, beta` are the roots of the quadratic equation `x^2 - (3 + 2^(sqrt(log_2 3)) -3^(sqrt( log_3 2)))x - 2(3^(log_3 2 - 2^(log_2 3))) = 0` then the value of `alpha^2 + alpha beta + beta^2` is equal to
View SolutionWhich of the following is not true for equation `x^(2)log8-xlog5=2(log2)-x` (A) equation has one integral root (B) equation has no irrational roots (C) equation has rational roots (D) none of these
04:58View SolutionLet `f(x)` be a quadratic expression such that `f(-1)+f(2)=0`. If one root of `f(x)=0` is `3`, then the other root of `f(x)=0` lies in (A) `(-oo,-3)` (B) `(-3,oo)` (C) `(0,5)` (D) `(5,oo)`
03:07View SolutionIf `f(x)=(x^(2)+3x+2)(x^(2)-7x+a)` and `g(x)=(x^(2)-x-12)(x^(2)+5x+b)`, then the value of `a` and `b`, if `(x+1)(x-4)` is H.C.F. of `f(x)` and `g(x)` is
07:19View SolutionThe remainder obtained when the polynomial `x+x^(3)+x^(9)+x^(27)+x^(81)+x^(243)` is divided by `x^(2)-1` is
04:36View SolutionLet `f(x)=x^(2)-ax+b`, `'a'` is odd positive integar and the roots of the equation `f(x)=0` are two distinct prime numbers. If `a+b=35`, then the value of `f(10)=`
09:49View SolutionIf `0 lt alpha lt beta lt gamma lt pi//2`, then the equation
`(x-sinbeta)(x-singamma)+(x-sinalpha)(x-singamma)+(x-sinalpha)(x-sinbeta)=0` has02:41View SolutionIf the system of equation `r^(2)+s^(2)=t` and `r+s+t=(k-3)/(2)` has exactly one real solution, then the value of `k` is
03:50View SolutionIf `a,` b`. `c in R` and `3b^(2)-8ac lt 0`, then the equation `ax^(4)+bx^(3)+cx^(2)+5x-7=0` has
01:49View SolutionFor real solution of equation `3sqrt(x+3p+1)-3sqrt(x)=1`, we have
03:22View SolutionFor `a`, `b`,`c` non-zero, real distinct, the equation, `(a^(2)+b^(2))x^(2)-2b(a+c)x+b^(2)+c^(2)=0` has non-zero real roots. One of these roots is also the root of the equation :
01:45View SolutionThe equation `x^(2)+bx+c=0` has distinct roots. If `2` is subtracted from each root the result are the reciprocal of the original roots, then `b^(2)+c^(2)` is
03:57View SolutionThe equation `(x^(2)+3x+4)^(2)+3(x^(2)+3x+4)+4=x` has
01:41View SolutionIf one root of the equation `(x-1)(7-x)=m` is three times the other, then `m` is equal to
02:48View SolutionIf the roots of the equation `ax^(2)-4x+a^(2)=0` are imaginery and the sum of the roots is equal to their product then `a` is
05:04View SolutionIf the sum of squares of roots of equation `x^(2)-(sin alpha-2)x-(1+sin alpha)=0` is the least, then `alpha` is equal to
07:53View SolutionIf `alpha` and `beta` are the roots of the equation `ax^(2)+bx+c=0` then the sum of the roots of the equation `a^(2)x^(2)+(b^(2)-2ac)x+b^(2)-4ac=0` is
03:18View SolutionIf the roots of the quadratic equation `ax^(2)+bx-b=0`, where `a`, `b in R` such that `a*b gt 0`, are `alpha` and `beta`, then the value of `log_(|(beta-1)|)|(alpha-1)|` is
07:45View SolutionIf `cos^4 alpha +k and sin^4 alpha+k` are the roots of `x^2+lambda(2 x+1)=0 and sin^2 alpha+1 and cos^2 alpha +1` are the roots of `x^2 +8 x+4=0,` then the sum of the possible values of `lambda` is
04:43View SolutionLet `f(x)=ax^(2)+bx+c`, `g(x)=ax^(2)+qx+r`, where `a`, `b`, `c`,`q`, `r in R` and `a lt 0`. If `alpha`, `beta` are the roots of `f(x)=0` and `alpha+delta`, `beta+delta` are the roots of `g(x)=0`, then
02:30View SolutionIf `a, b` and `c` are in geometric progression and the roots of the equation `ax^(2) + 2bx + c = 0` are `alpha` and `beta` and those of `cx^(2) + 2bx + a = 0` are `gamma` and `delta`
04:51View SolutionIf `alpha`, `beta` are the roots of the equation `ax^(2)+bx+c=0` and `S_(n)=alpha^(n)+beta^(n)`, then `aS_(n+1)+bS_(n)+cS_(n-1)=(n ge 2)`
04:19View SolutionLet `f(x)=ax^(2)+bx+c`, `g(x)=ax^(2)+px+q`, where `a`, `b`, `c`, `q`, `p in R` and `b ne p`. If their discriminants are equal and `f(x)=g(x)` has a root `alpha`, then
06:17View SolutionIf `alpha` and `beta` be the roots of equation `x^(2) + 3x + 1 = 0` then the value of `((alpha)/(1 + beta))^(2) + ((beta)/(1 + alpha))^(2)` is equal to
03:46View SolutionThe roots of the equation `a(b-2c)x^(2)+b(c-2a)x+c(a-2b)=0` are, when `ab+bc+ca=0`
03:30View SolutionIf the equations `2x^(2)-7x+1=0` and `ax^(2)+bx+2=0` have a common root, then
03:06View SolutionIf `alpha` and `beta`, `alpha` and `gamma`, `alpha` and `delta` are the roots of the equations `ax^(2)+2bx+c=0`, `2bx^(2)+cx+a=0` and `cx^(2)+ax+2b=0` respectively where `a`, `b`, `c` are positive real numbers, then `alpha+alpha^(2)` is equal to
03:06View SolutionThe product of uncommon real roots of the polynomials ` p(x)=x^4+2x^3-8x^2-6x+15` and ` q(x) ` `= x^3+4x^2-x-10 ` is :
09:13View SolutionNumber of values of `x` satisfying the pair of quadratic equations `x^(2)-px+20=0` and `x^(2)-20x+p=0` for some `p in R` is
03:42View SolutionIf the equation `4x^2-x-1=0a n d3x^2+(lambda+mu)x+lambda-mu=0` have a root common, then the rational values of `lambdaa n dmu` are a.`lambda=(-3)/4` b. `lambda=0` c. `mu=3/4` b.`mu=0`
02:56View SolutionIf the equations `x^(2)+2lambdax+lambda^(2)+1=0`, `lambda in R` and `ax^(2)+bx+c=0` , where `a`, `b`, `c` are lengths of sides of triangle have a common root, then the possible range of values of `lambda` is
07:22View SolutionIf both the roots of `k(6x^(2)+3)+rx+2x^(2)-1=0` and `6k(2x^(2)+1)+px+4x^(2)-2=0` are common, then `2r-p` is equal to
03:35View Solution`x^(3)+5x^(2)+px+q=0` and `x^(3)+7x^(2)+px+r=0` have two roos in common. If their third roots are `gamma_(1)` and `gamma_(2)` , respectively, then `|gamma_(1)-gamma_(2)|=`
05:04View SolutionLet `a,b in N, a != b` and the two quadratic equations `(a-1)x^2-(a^2+2)x+a^2+2a=0 and (b-1)x^2-(b^2+2)x+(b^2+2b)=0` have a common root. The value of `ab` is
View SolutionA quadratic equations `p(x)=0` having coefficient `x^(2)` unity is such that `p(x)=0` and `p(p(p(x)))=0` have a common root, then
04:00View SolutionIf `ax^2+bx+c=0 and cx^2 + bx+a=0(a,b,c in R)` have a common non-real roots, then which of the following is not true ?
04:17View SolutionLet `A={x|x^2 + (m - 1)x -2(m +1)=0, x in R}, {B = {x|(m-1)x^2 + mx + 1 = 0, x in R}` Number of values of m such that `AuuB` has exactly 3 distinct elements, is
04:20View SolutionIf the equation `|x^2-5x + 6|-lambda x+7 lambda=0` has exactly 3 distinct solutions then `lambda` is equal to
06:20View SolutionLet `alpha`, `beta (a lt b)` be the roots of the equation `ax^(2)+bx+c=0`. If `lim_(xtom) (|ax^(2)+bx+c|)/(ax^(2)+bx+c)=1` then
03:01View SolutionIf the quadratic polynomials defined on real coefficient
`P(x)=a_(1)x^(2)+2b_(1)x+c_(1)` and `Q(x)=a_(2)x^(2)+2b_(2)x+c_(2)` take positive values `AA x in R`, what can we say for the trinomial `g(x)=a_(1)a_(2)x^(2)+b_(1)b_(2)x+c_(1)c_(2)` ?03:57View SolutionFor which of the following graphs the quadratic expression `y=ax^(2)+bx+c` the product `abc` is negative ?
03:47View SolutionThe difference of maximum and minimum value of `(x^(2)+4x+9)/(x^(2)+9)` is
05:23View SolutionIf `a gt 1` , then the roots of the equation `(1-a)x^(2)+3ax-1=0` are
05:14View SolutionThe set of values of `a` for which `a x^2+(a-2)x-2` is negative for exactly two integral `x ,` is `(0,2)` b. `[1,2)` c. `(1,2]` d. `(0,2]`
05:57View SolutionIf the roots of equation `(a + 1)x^2-3ax + 4a = 0` (a is not equals to -1) are greater than unity, then
02:12View SolutionThe equation `ax^(4)-2x^(2)-(a-1)=0` will have real and unequal roots if
04:10View SolutionIf `ax^(2)+bx+c=0`, `a ne 0`, `a`, `b`, `c in R` has distinct real roots in `(1,2)`, then `a` and `5a+2b+c` have
05:23View SolutionIf `c lt a lt b lt d`, then roots of the equation `bx^(2)+(1-b(c+d)x+bcd-a=0`
06:09View SolutionIf `2a`, `b`, `2c` are in `A.P.` where `a`, `b`, `c` are `R^(+)`, then the expression `f(x)=(ax^(2)-bx+c)` has
03:55View SolutionIf `a`, `b`, `c` are positive numbers such that `a gt b gt c` and the equation `(a+b-2c)x^(2)+(b+c-2a)x+(c+a-2b)=0` has a root in the interval `(-1,0)`, then
05:01View SolutionIf the quadratic equation `x^(2)-36x+lambda=0` has roots `alpha` and `beta` such that `alpha`, `beta in N` and `(lambda)/(5) cancel in Z` and `lambda` assumes minimum possible value then `(sqrt(alpha+2)sqrt(beta+2))/(|alpha-beta|)` is equal to
04:40View SolutionIf the equation `2^(2x)+a*2^(x+1)+a+1=0` has roots of opposite sign, then the exhaustive set of real values of `a` is
02:49View SolutionLet `a`, `b`, `c` ne three distinct non-zero real numbers satisfying the system of equation `(1)/(a)+(1)/(a-1)+(1)/(a-2)=1` , `(1)/(b)+(1)/(b-1)+(1)/(b-2)=1` , `(1)/(c )+(1)/(c-1)+(1)/(c-2)=1`. Then `abc=`
03:57View SolutionIn the given figure graph of `y=p(x)=x^(4)+ax^(3)+bx^(2)+cx+d` is given
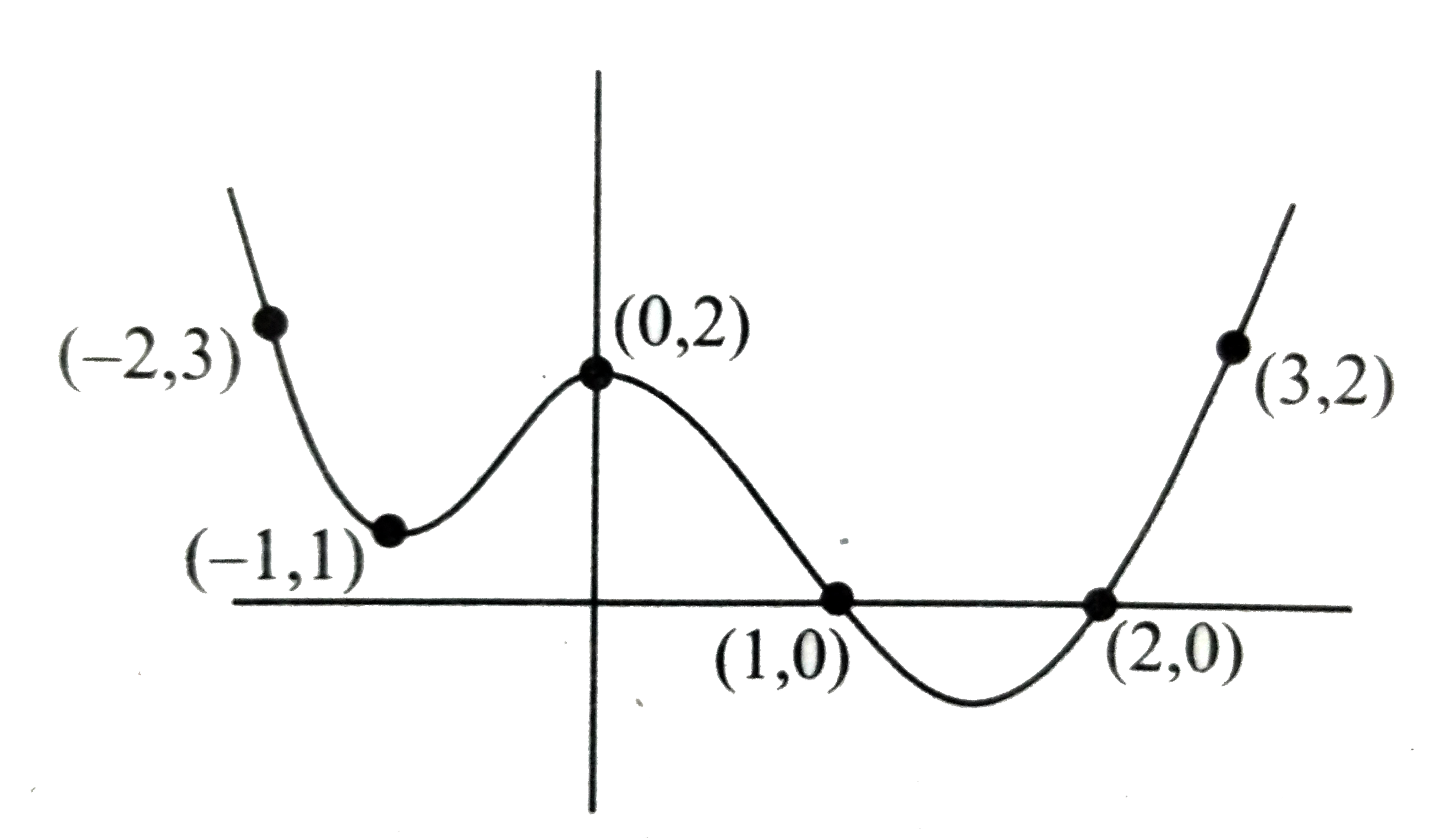
The product of all imaginery roots of `p(x)=(0)` is03:28View SolutionIf `a^(3)-3a^(2)+5a-17=0` and `b^(3)-3b^(2)+5b+11=0` are such that `a+b` is a real number, then the value of `a+b` is
06:44View SolutionLet` f(x) = x^4 + ax^3 + bx^2 + cx + d` be a polynomial with real coefficients and real roots. If |f(i)|=1where `i=sqrt(-1)`, then the value of a +b+c+d is
04:02View SolutionIf f(x) is a polynomial of degree four with leading coefficient one satisfying `f(1)=1, f(2)=2,f(3)=3`.then `[(f(-1)+f(5))/(f(0)+f(4))]`
11:19View SolutionLet `p(x) =x^6-x^5-x^3-x^2-x` and `alpha, beta, gamma, delta` are the roots of the equation `x^4-x^3-x^2-1=0` then `P(alpha)+P(beta)+P(gamma)+P(delta)=`
03:30View SolutionThe line `y=mx+1` touches the curves `y=0x^(4)+2x^(2)+x` at two points `P(x_(1),y_(1))` and `Q(x_(2),y_(2))`. The value of `x_(1)^(2)+x_(2)^(2)+y_(1)^(2)+y_(2)^(2)` is
04:10View SolutionIf `a+b+c=24`, `a^(2)+b^(2)+c^(2)=210`, `abc=440`. Then the least value of `a-b-c` is
05:27View SolutionIf the roots of `x^(4)+qx^(2)+kx+225=0` are in arthmetic progression, then the value of `q`, is
03:41View Solution
Single correct Answer questions and complete solutions for chapter THEORY OF EQUATIONS of CENGAGE of Class 12
All Exercises from CENGAGE NEW DPP Class 12 MATHS THEORY OF EQUATIONS
- Comprehension
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 2.1
- Exercise 2.10
- Exercise 2.11
- Exercise 2.12
- Exercise 2.13
- Exercise 2.2
- Exercise 2.3
- Exercise 2.4
- Exercise 2.5
- Exercise 2.6
- Exercise 2.7
- Exercise 2.8
- Exercise 2.9
- JEE Advanced Previous Year
- JEE Main Previous Year
- Multiple Correct Answer
- Single correct Answer
