Complete Solutions to Comprehension of chapter PROGRESSION AND SERIES of Class 12 book with complete answers and questions

The `1^(st)` , `2^(nd)` and `3^(rd)` terms of an arithmetic series are `a`, `b` and `a^(2)` where `'a'` is negative. The `1^(st)`, `2^(nd)` and `3^(rd)` terms of a geometric series are `a`, `a^(2)` and `b` respectively.
The sum of infinite geometric series is

The `1^(st)` , `2^(nd)` and `3^(rd)` terms of an arithmetic series are `a`, `b` and `a^(2)` where `'a'` is negative. The `1^(st)`, `2^(nd)` and `3^(rd)` terms of a geometric series are `a`, `a^(2)` and `b` respectively.
The sum of the `40` terms of the arithmetic series is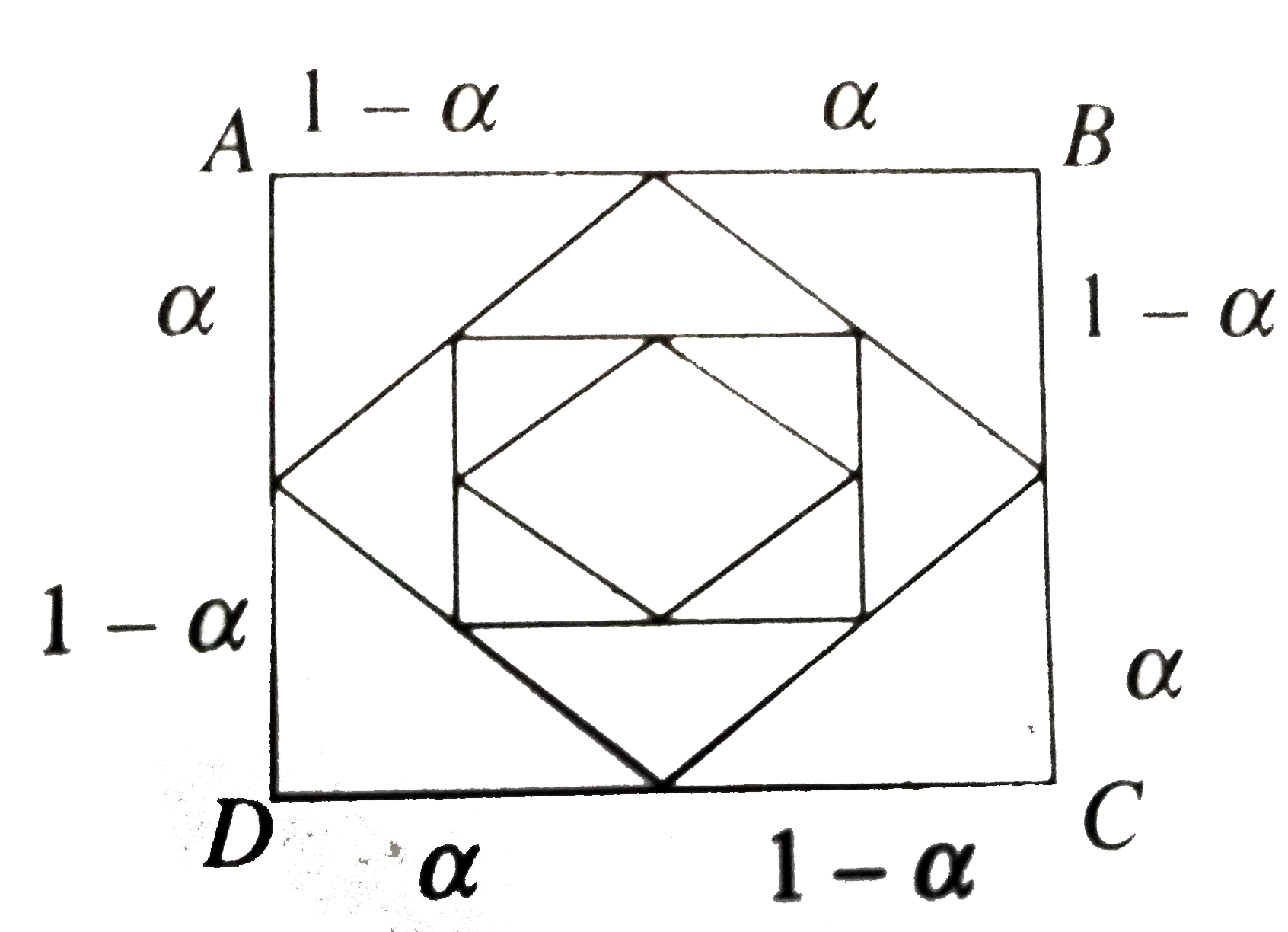

Let `ABCD` is a unit square and each side of the square is divided in the ratio `alpha : (1-alpha) (0 lt alpha lt 1)` . These points are connected to obtain another square. The sides of new square are divided in the ratio `alpha : (1-alpha)` and points are joined to obtain another square. The process is continued idefinitely. Let `a_(n)` denote the length of side and `A_(n)` the area of the `n^(th)` square
If`alpha=(1)/(3)`, then the least value of `n` for which `A_(n) lt (1)/(10)` is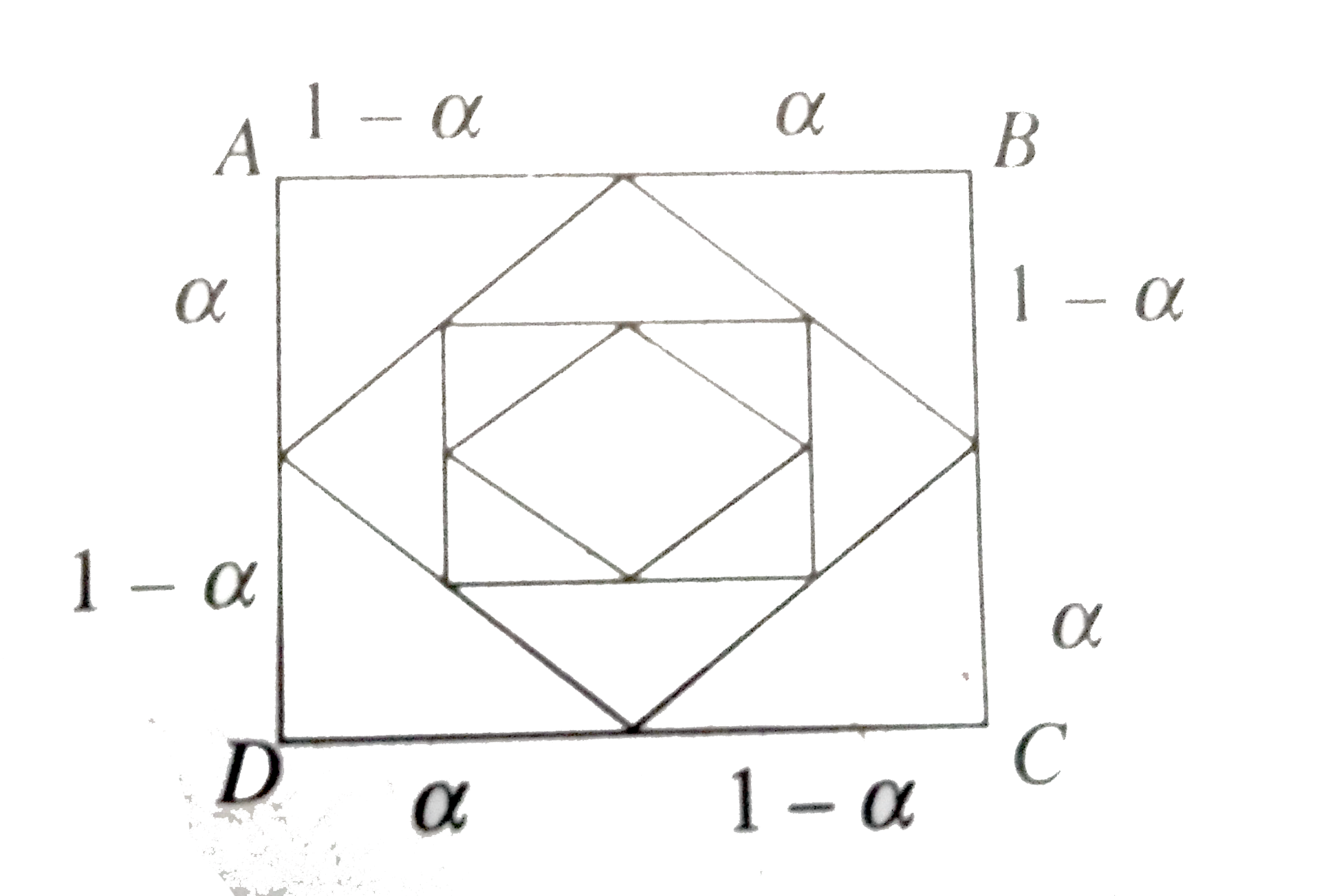

Let `ABCD` is a unit square and each side of the square is divided in the ratio `alpha : (1-alpha) (0 lt alpha lt 1)` . These points are connected to obtain another square. The sides of new square are divided in the ratio `alpha : (1-alpha)` and points are joined to obtain another square. The process is continued idefinitely. Let `a_(n)` denote the length of side and `A_(n)` the area of the `n^(th)` square
The value of `alpha` for which `sum_(n=1)^(oo)A_(n)=(8)/(3)` is/are

Let `ABCD` is a unit square and each side of the square is divided in the ratio `alpha : (1-alpha) (0 lt alpha lt 1)` . These points are connected to obtain another square. The sides of new square are divided in the ratio `alpha : (1-alpha)` and points are joined to obtain another square. The process is continued idefinitely. Let `a_(n)` denote the length of side and `A_(n)` the area of the `n^(th)` square
The value of `alpha` for which side of `n^(th)` square equal to the diagonal of `(n+1)^(th)` square is

Let `f(n)` denote the `n^(th)` terms of the seqence of `3,6,11,18,27,….` and `g(n)` denote the `n^(th)` terms of the seqence of `3,7,13,21,….` Let `F(n)` and `G(n)` denote the sum of `n` terms of the above sequences, respectively. Now answer the following:
`lim_(ntooo)(f(n))/(g(n))=`

Let `f(n)` denote the `n^(th)` terms of the seqence of `3,6,11,18,27,….` and `g(n)` denote the `n^(th)` terms of the seqence of `3,7,13,21,….` Let `F(n)` and `G(n)` denote the sum of `n` terms of the above sequences, respectively. Now answer the following:
`lim_(ntooo)(f(n))/(g(n))=`