Complete Solutions to Exercise (Comprehension) of chapter AREA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AREA |
| CENGAGE NEW | Exercise (Comprehension) |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Let `A_(r)` be the area of the region bounded between the curves `y^(2)=(e^(-kr))x("where "k gt0,r in N)" and the line "y=mx ("where "m ne 0)`, k and m are some constants
`A_(1),A_(2),A_(3),…` are in G.P. with common ratio10:02View SolutionLet `A_(r)` be the area of the region bounded between the curves `y^(2)=(e^(-kr))x("where "k gt0,r in N)" and the line "y=mx ("where "m ne 0)`, k and m are some constants
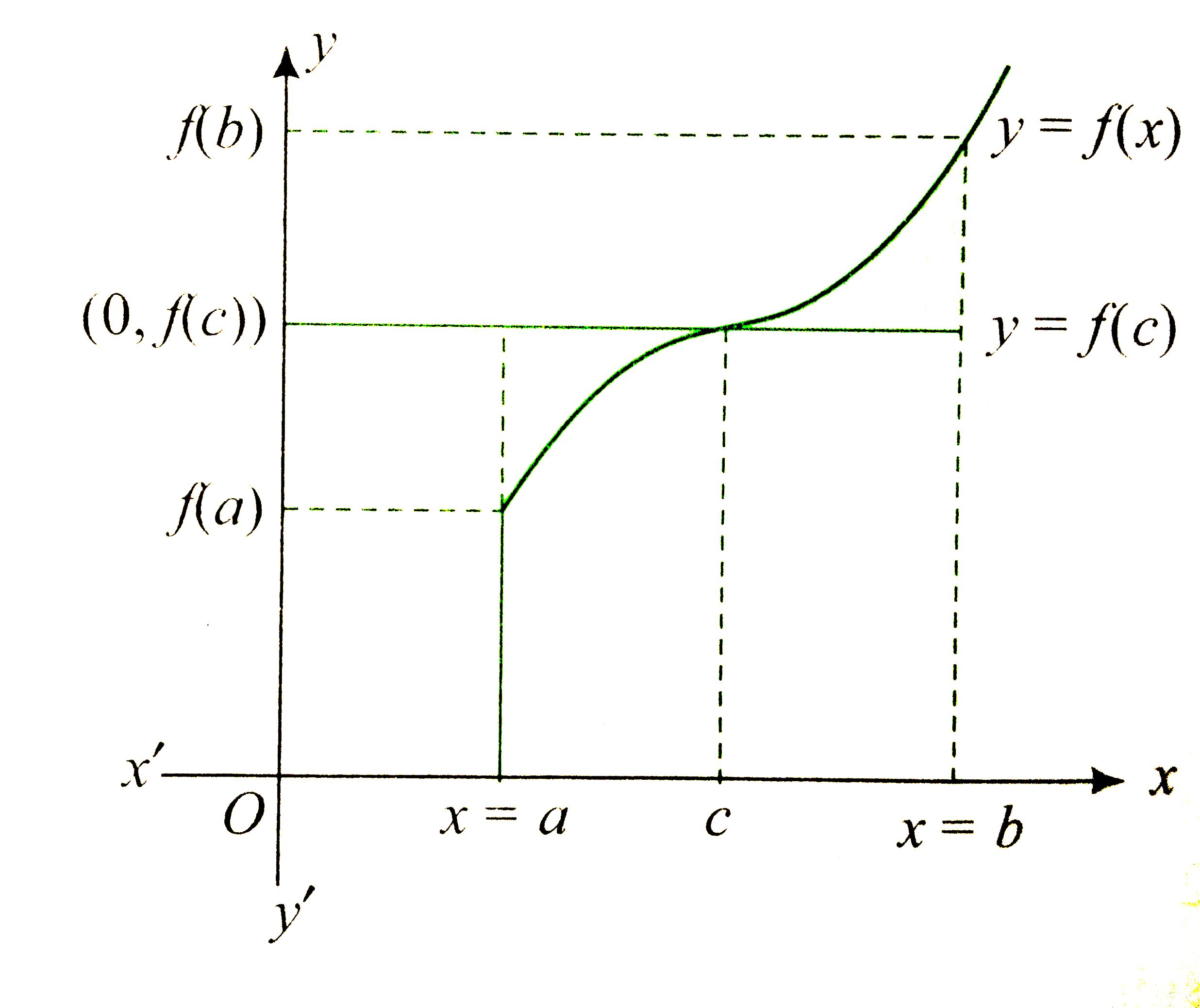
`lim_(n to oo)Sigma_(i=1)^(n)A_(i)=(1)/(48(e^(2k)-1))` then the value of m is10:13View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx`
`=f(c)(c-a)-int_(a)^(c)(f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
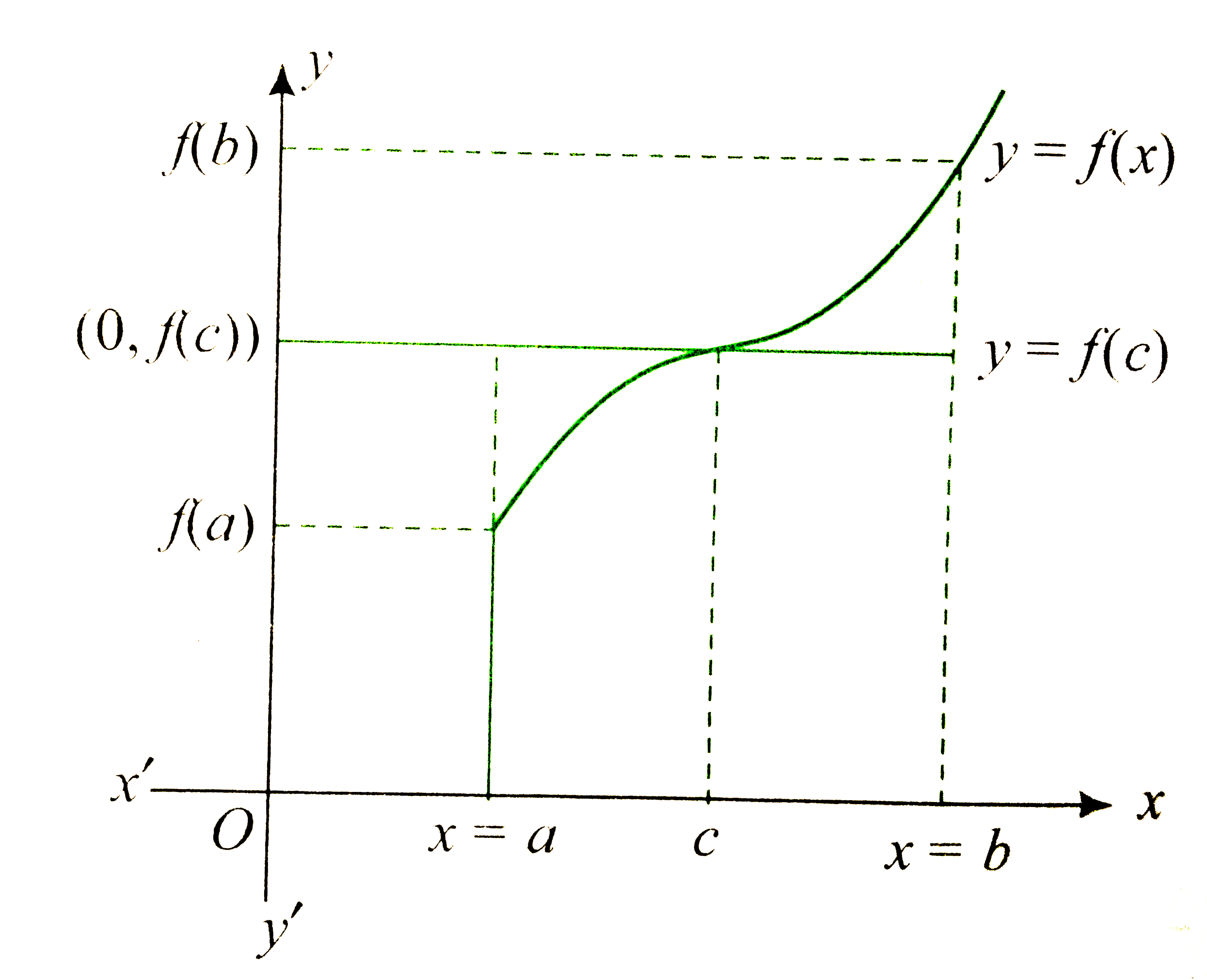
If the area bounded by `f(x)=(x^(3))/(3)-x^(2)+a` and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is01:40View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c) (f(c)-f(x))dx+int_(c)^(b) (f(c))dx`
`=f(c)(c-a)-int_(a)^(c) (f(x))dx+int_(a)^(b) (f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b) (f(x))dx-int_(a)^(c) (f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
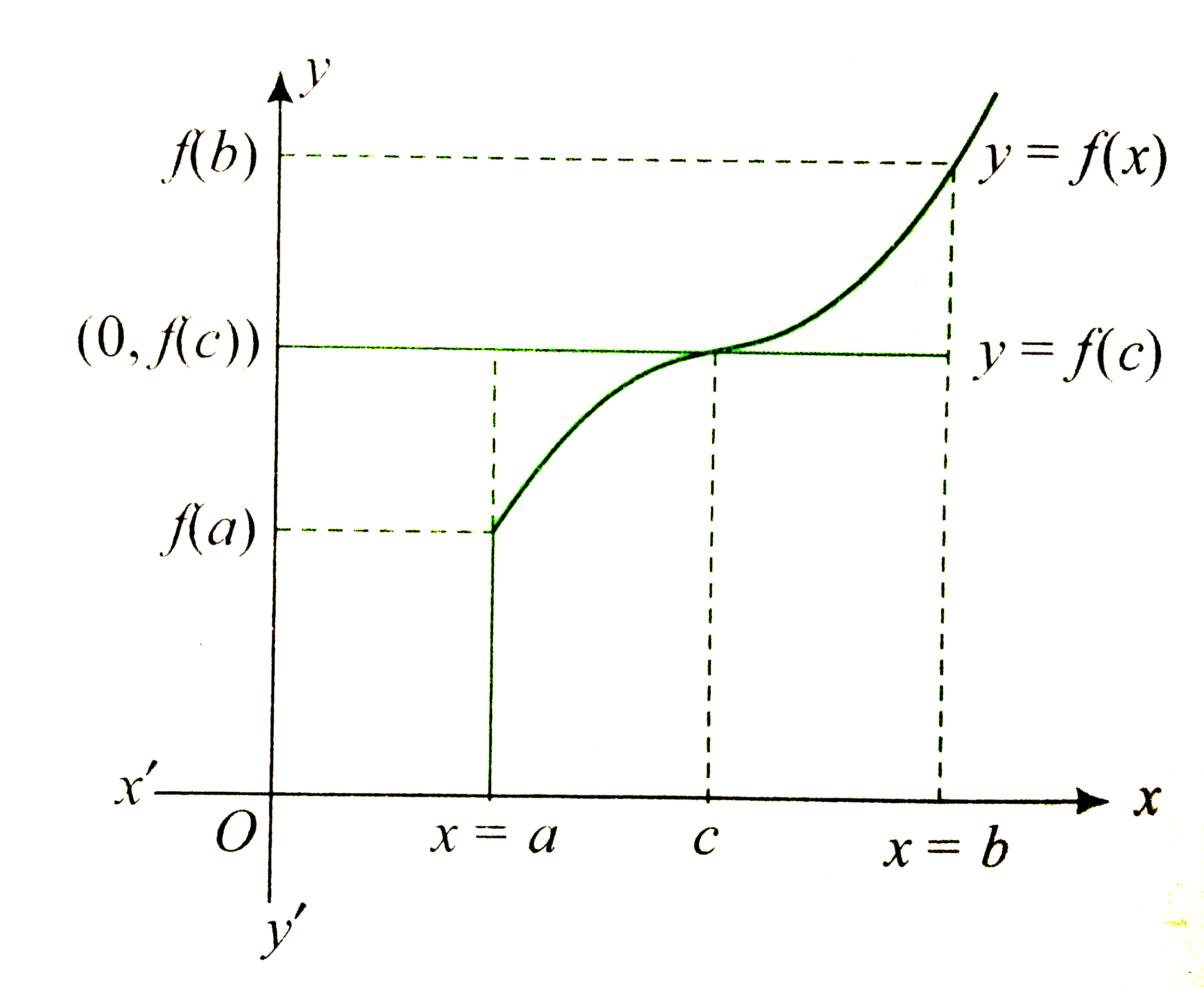
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function `y=x^(3)+3x^(2)+x+a`, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is01:25View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx`
`=f(c)(c-a)-int_(a)^(c) (f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
If the area enclosed by `f(x)= sin x + cos x, y=a` between two consecutive points of extremum is minimum, then the value of a is02:33View SolutionConsider the area `S_(0),S_(1),S_(2)….` bounded by the x-axis and half-waves of the curve `y=e^(-x) sin x," where "x ge 0.`
The value of `S_(0)` is02:28View SolutionConsider the sequence of natural numbers `s_0,s_1,s_2`,... such that `s_0 =3, s_1 = 3 and s_n = 3 + s_(n-1) s_(n-2)`, then
04:25View SolutionConsider the area `S_(0),S_(1),S_(2)….` bounded by the x-axis and half-waves of the curve `y=e^(-x) sin x," where "x ge 0.`
`Sigma_(n=0)^(oo) S_(n)` is equal to03:49View Solution`"Two curves "C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12," satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by `C_(1) and C_(2)` isView Solution`"Two curves "C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12," satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by the curve `C_(2) and |x|+|y|=sqrt(12)` isView Solution`"Two curves "C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12," satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by `C_(1) and x+y+2=0` isView SolutionConsider the two curves `C_(1):y=1+cos x and C_(2): y=1 + cos (x-alpha)" for "alpha in (0,(pi)/(2))," where "x in [0,pi].` Also the area of the figure bounded by the curves `C_(1),C_(2), and x=0` is same as that of the figure bounded by `C_(2),y=1, and x=pi`.
The value of `alpha` is03:54View SolutionConsider two curves `C_1:y =1/x` and `C_2.y=lnx` on the `xy` plane. Let `D_1`, denotes the region surrounded by `C_1,C_2` and the line `x = 1` and `D_2` denotes the region surrounded by `C_1, C_2` and the line `x=a`, Find the value of `a`
06:20View SolutionConsider the function defined implicity by the equation `y^(2)-2ye^(sin^(-1)x)+x^(2)-1+[x]+e^(2sin ^(-1)x)=0("where [x] denotes the greatest integer function").`
The area of the region bounded by the curve and the line `x=-1` isView SolutionConsider the function defined implicity by the equation `y^(2)-2ye^(sin^(-1)x)+x^(2)-1+[x]+e^(2sin ^(-1)x)=0("where [x] denotes the greatest integer function").`
Line x=0 divides the region mentioned above in two parts. The ratio of area of left-hand side of line to that of right-hand side of line isView SolutionConsider two functions `f (x) ={[x] , -2 leq x leq -1 and |x|+1 , -1 lt x leq 2 and g(x)={[x], -pi leq x lt 0 and sin x and 0 leq x leq pi`, where [.] denotes the greatest integer function.
08:34View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta)y(t)x'(t)dt,`
`S=int_(alpha)^(beta)x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the region bounded by an are of the cycloid `x=a(t-sin t), y=a(1- cos t)` and the x-axis is02:08View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta)y(t)x'(t)dt,`
`S=int_(alpha)^(beta)x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the loop described as
`x=(t)/(3)(6-t),y=(t^(2))/(8)(6-t)` is01:56View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta) y(t)x'(t)dt,`
`S=int_(alpha)^(beta) x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
If the curve given by parametric equation `x=t-t^(3), y=1-t^(4)` forms a loop for all values of `t in [-1,1]` then the area of the loop is01:53View SolutionLet f(x) be a continuous function fiven by `f(x)={(2x",", |x|le1),(x^(2)+ax+b",",|x|gt1):},"then "`
If f(x) is continuous for all real x then the value of `a^(2)+b^(2)` is04:02View SolutionLet `f(x)` be continuous function given by `f(x)={2x ,|x|lt=1x^2+a x+b ,|x|>1}dot` Find the area of the region in the third quadrant bounded by the curves `x=-2y^2a n dy=f(x)` lying on the left of the line `8x+1=0.`
09:53View Solution
Exercise (Comprehension) questions and complete solutions for chapter AREA of CENGAGE MATHS (HINGLISH) of Class 12
