Complete Solutions to Concept Exercise 2.1 of chapter SOURCES OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCES OF MAGNETIC FIELD |
| CENGAGE PHYSICS | Concept Exercise 2.1 |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
(a). Find the magnetic field B at point O (centre) of
(i). ABCD, which is a square of side l.
(ii). ABC, which is an equilateral triangle of side l.
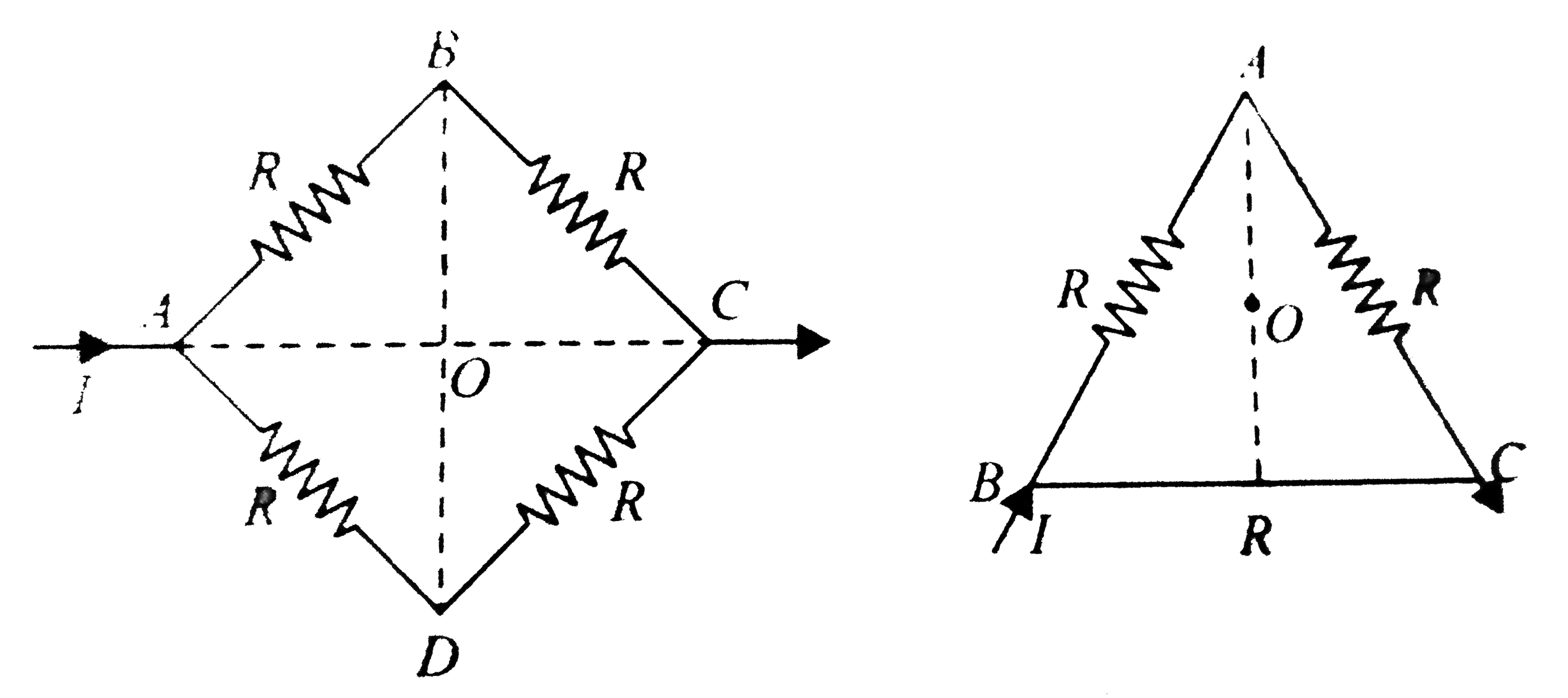
(b) Twelve uniform wires of equal length l and each of resistance r are connected to form a skelton cube. A battary of emf E is connected between two diagonally opposite corners of the cube. The magnetic induction at the centreof the cube is .........
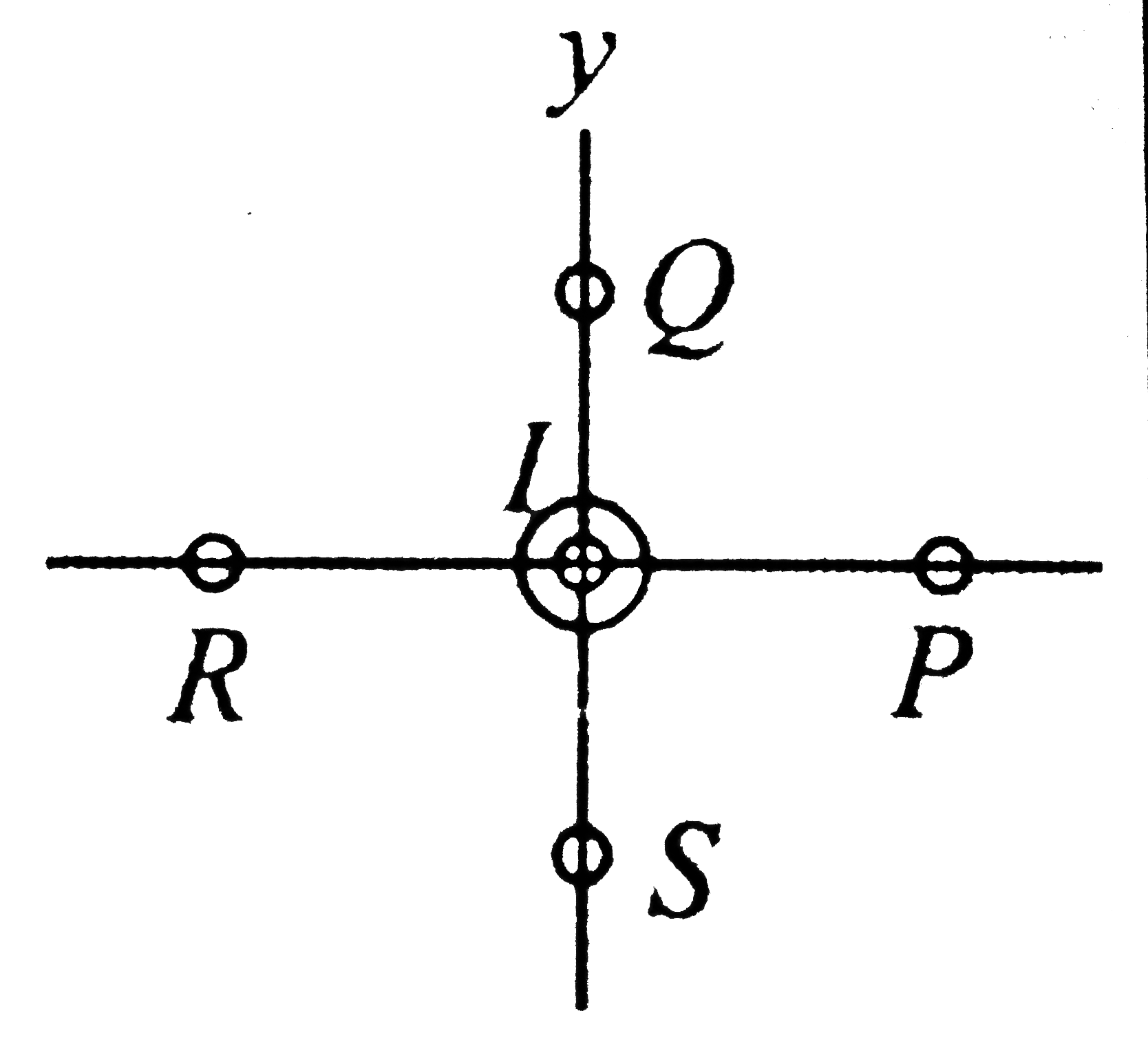
(c) An infinately long straight wire is placed at the origin along the z-axis. The current I flows along the positive z-axis. Find the unit vecotrs showing the direction of magnetic field at the four points: `P(a,0), Q(0,b), R(a,0) and S(0,-b)`

View SolutionCalculate the magnetic field at point O in each of the following cases:




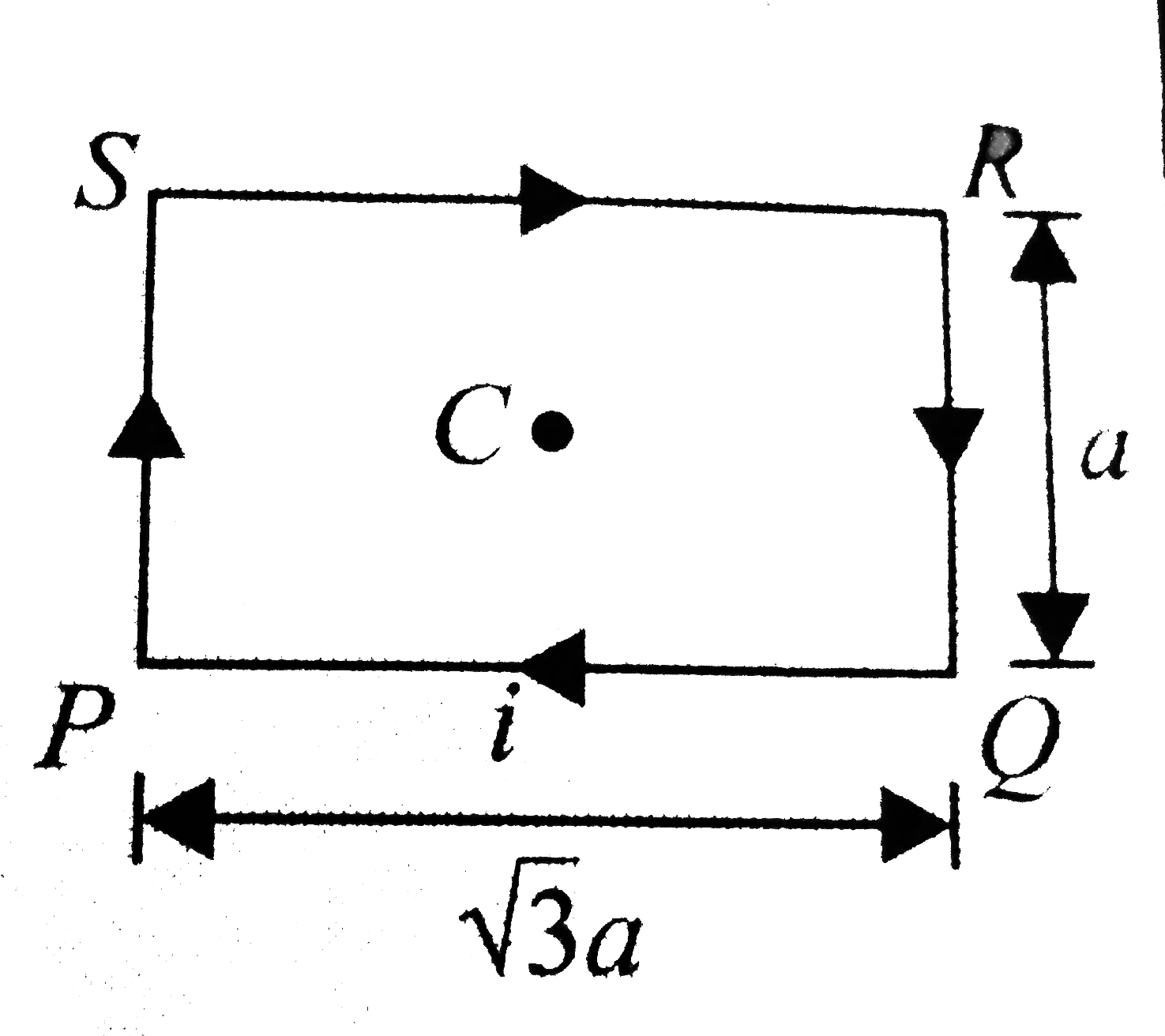
View SolutionFind resultant magnetic field at C in Fig
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

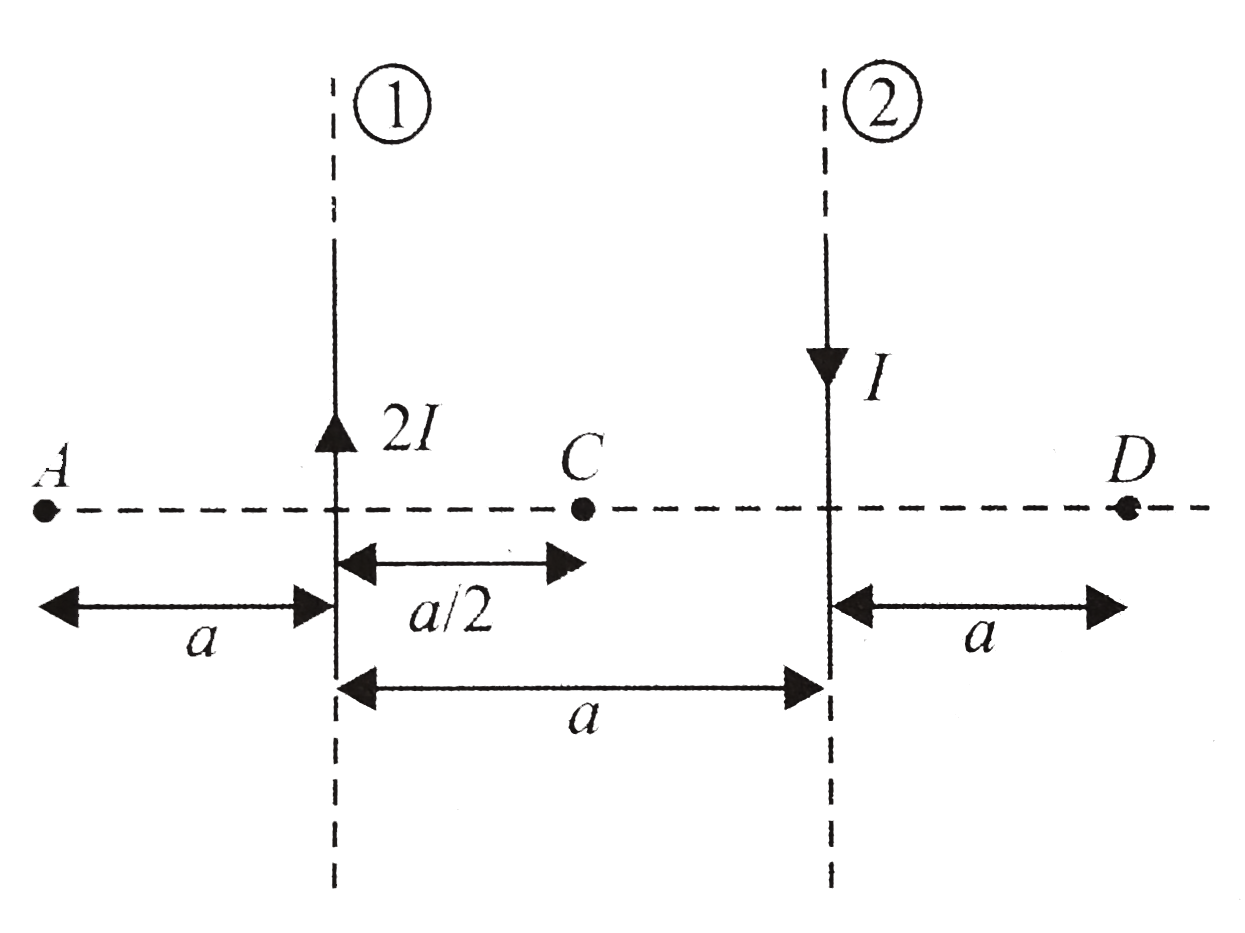
View SolutionIn Fig. There are two parallel long wires (placed in the plane of paper ) carrying currents 2I and I. Consider point A,C and D on the line perpendicular to both the wires and also in the plane of the paper. The distances are mentioned. Find (a) `vecB` at A,C and D (b) position of points on line ACD where `vecB` 0 is.
View SolutionIn Fig. a larger metal sheet of width w carries a current I(uniformly distributed in its width w). Find the magnetic field at point P which lies on the plane of the sheet.


View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View SolutionFind magnetic field at C by the system of current carrying wire.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity `omega` about its axes. Find the magnetic field at the centre of the ring.

View SolutionSuppose that the current density in a wire of radius a varius with r according to `Kr^2` where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) r`lt`a and (b) r`gt`a.
View SolutionIn Fig. Find the magnetic field at common centre.

View SolutionThe segment of wire shown in figure carries a current of `i = 5.0 A` where the radius of the circular arc is `R = 3.0 cm`. Determine the magnitude and direction of the magnetic field at the origin.
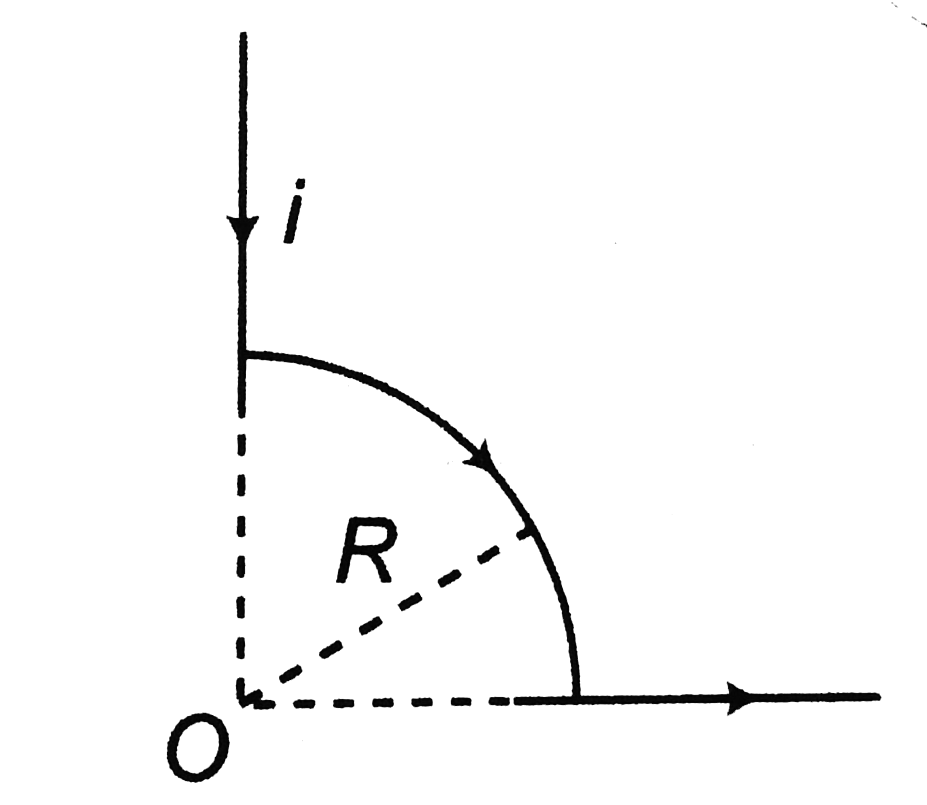
View SolutionA long, straight wire, carrying a current 200A, runs through a cubical wooden box, entering and leaving through holes in the centre of opposite faces (as shown in Fig). The length of each side of the box is 20 cm. Consider an element `dl,0.100 cm` long of the wire at the centre of the box. Compute the magnitude dB of the magnetic field produced by this element at the point a, b,c,d and e as shown fig. Points a,c, and dare at the centres of the faces of the cube, point b is at the midpoint of one edge, and point e is at a corner. Copy the figure and show the direction and relative magnitudes of field vectors.

View SolutionThe wire shown in Fig. carries current I in the direction shown. The wire consists of a very long, straight section, a quarter- circle with radius R, and another long, straight section. What are magnitude and direction of net magnetic field at the center of curvature of quarter-circle section (point P)?

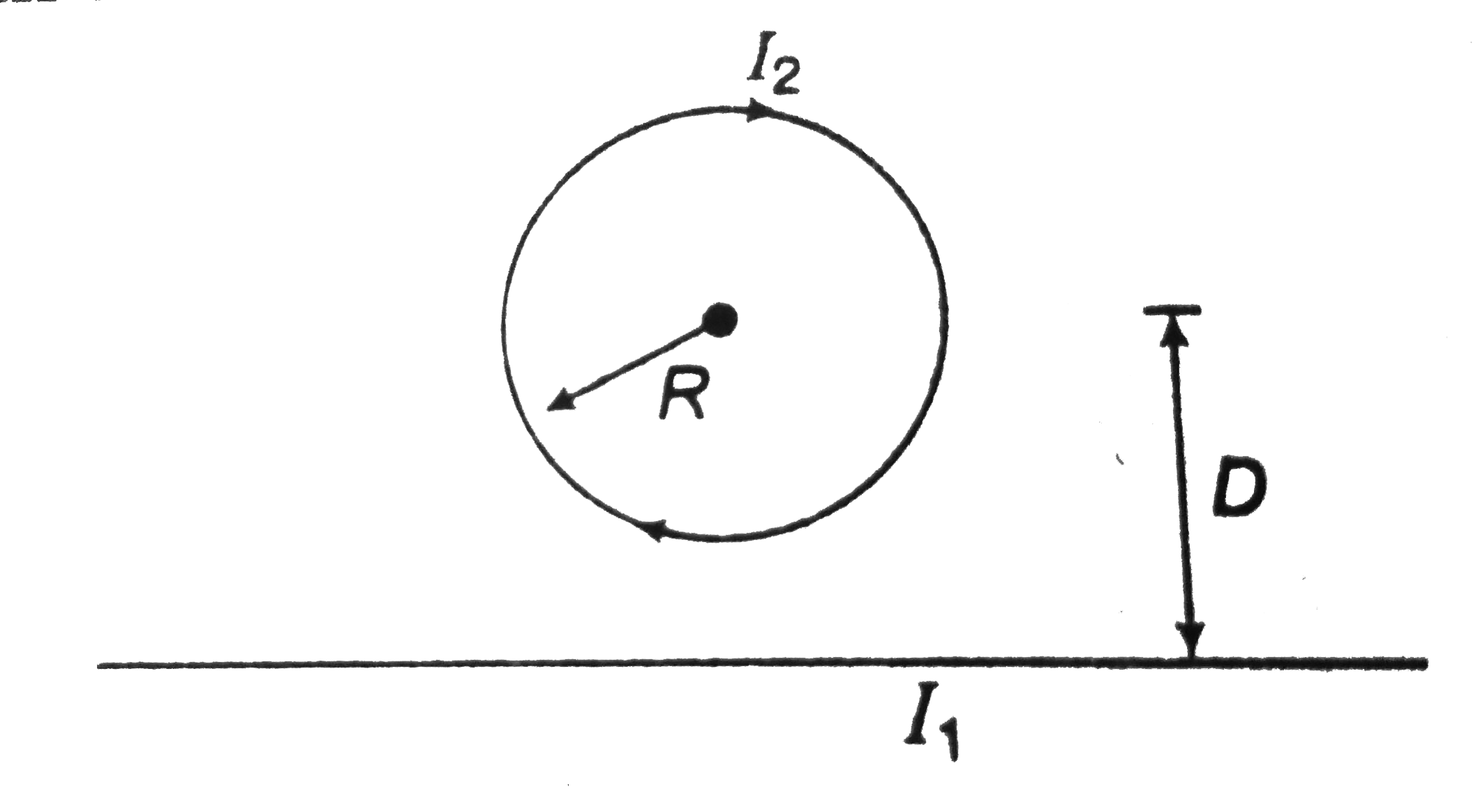
View SolutionA circular loop of radius `R` carries current `I_2` in a clockwise direction as shown in figure. The centre of the loop is a distance `D` above a long, straight wire. What are the magnitude and direction of the current `I_1` in the wire if the magnetic field at the centre of loop is zero?
View SolutionFor the arrangement shown in Fig. determine the magnetic field at centre O.

View SolutionFour long, parallel conductors carry equal currents of `5.0`. The direction of the currents is into the pge at points. `A` and `B` and out of the page at `C` and `D`. Calculate the magnitude and directionof the mgnetic field at point `P`, located at the centre of the square.

View SolutionA long vertical wire carrying a current of 10A in the upward direction is placed in a region where a horizontal magnetic field of magnitude`2.0 xx 10^-3` T exists from south to north. Find the point where the resultant magnetic field is zero.
View SolutionFigure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the points P,Q, R and S are equal and find this magnitude. `

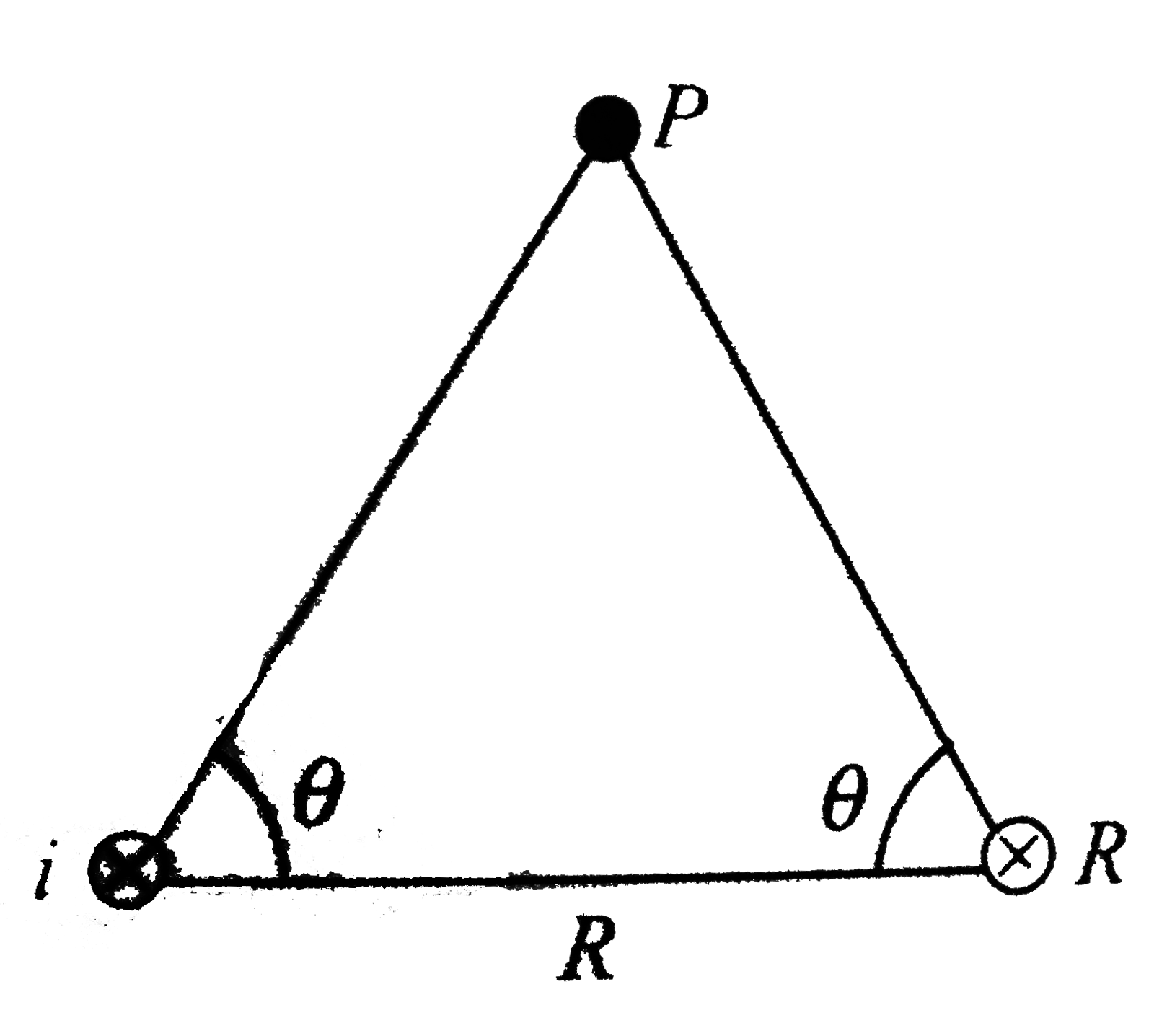
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle `theta` from the plane of the wires.
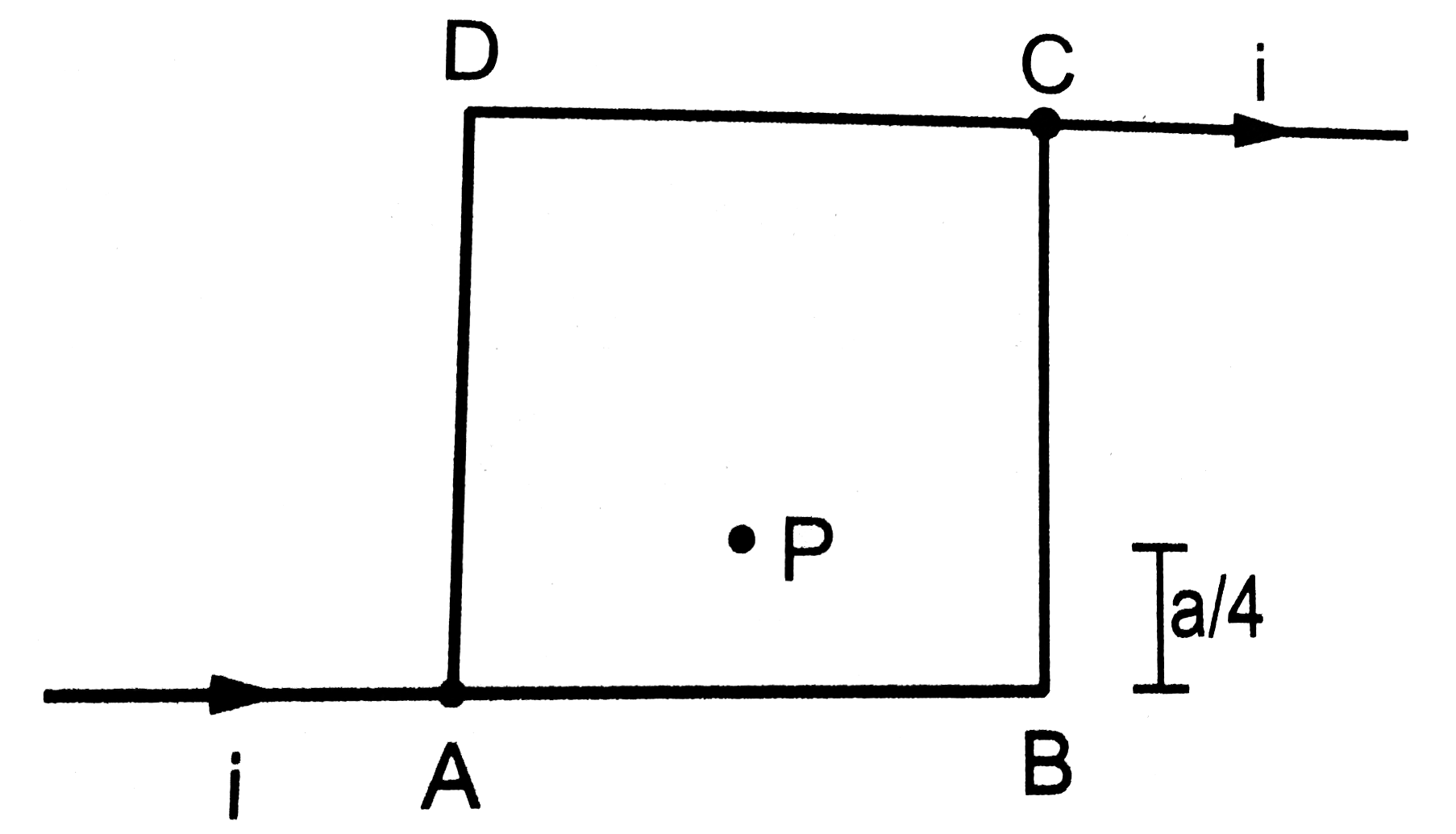
View SolutionFigure shows a square loop of edge `a` made of a uniform wire. A current `i` enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it. `
View SolutionLet two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at `x=0`, the other at `x=d` (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.

View SolutionA long, circular pipe, with an outside radius R, carries a (uniformly distributed) current `i_0` (into the paper as shown in Fig.) A wire runs parallel to the pipe at a distance 3R from centre to centre. Calculate the magnitude and direction of the current in the wire that would cause the resultant magnetic field at point P to have the same magnitude, but the opposite direction, as the resultant field at the centre of the pipe.

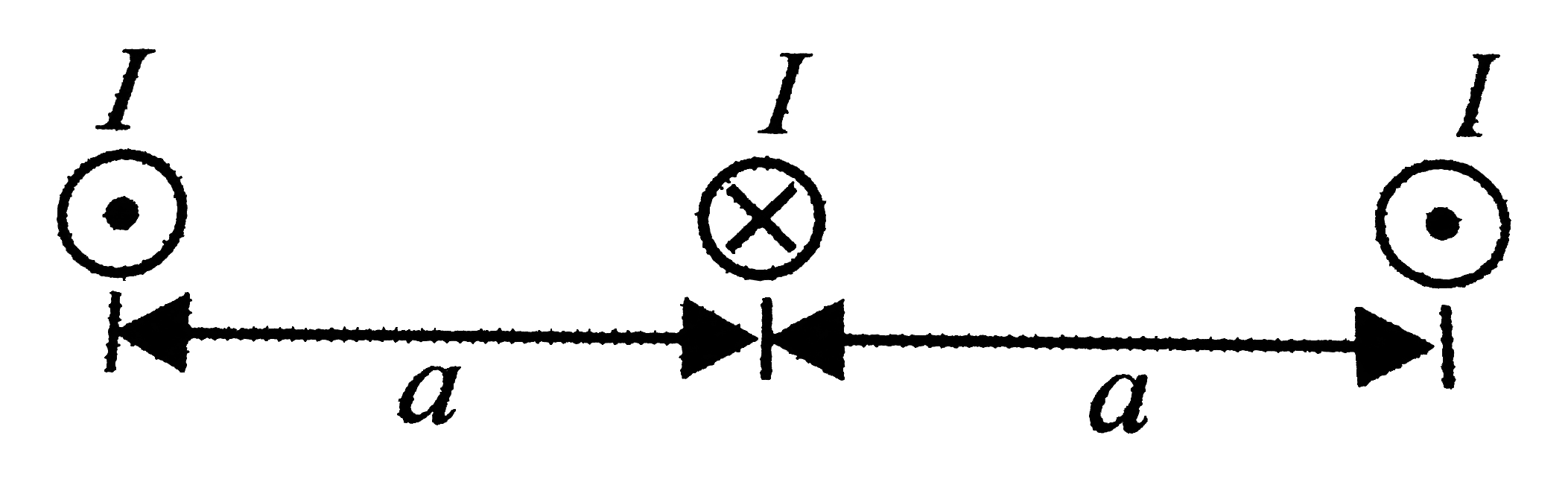
View SolutionShown in Fig. is an end-on view of three long, straight, parallel conductors spaced equal distances a apart. The outer conductors carry current I out of the page, the middle conductor carries current I into the page. Where in the plane of the page is the magnetic field zero?
View SolutionIn Fig, find the magnetic field at point P.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionA wire is bent into the shape shown in fig and the magnetic field is measured at `P_1` when the current in the wire is I. The same wire is then formed into the shape shown in the Fig and the magnetic field is measured at point `P_2` when the current is again I. If the total length of wire is the same in each case, what is the ratio of `B_1//B_2` ?
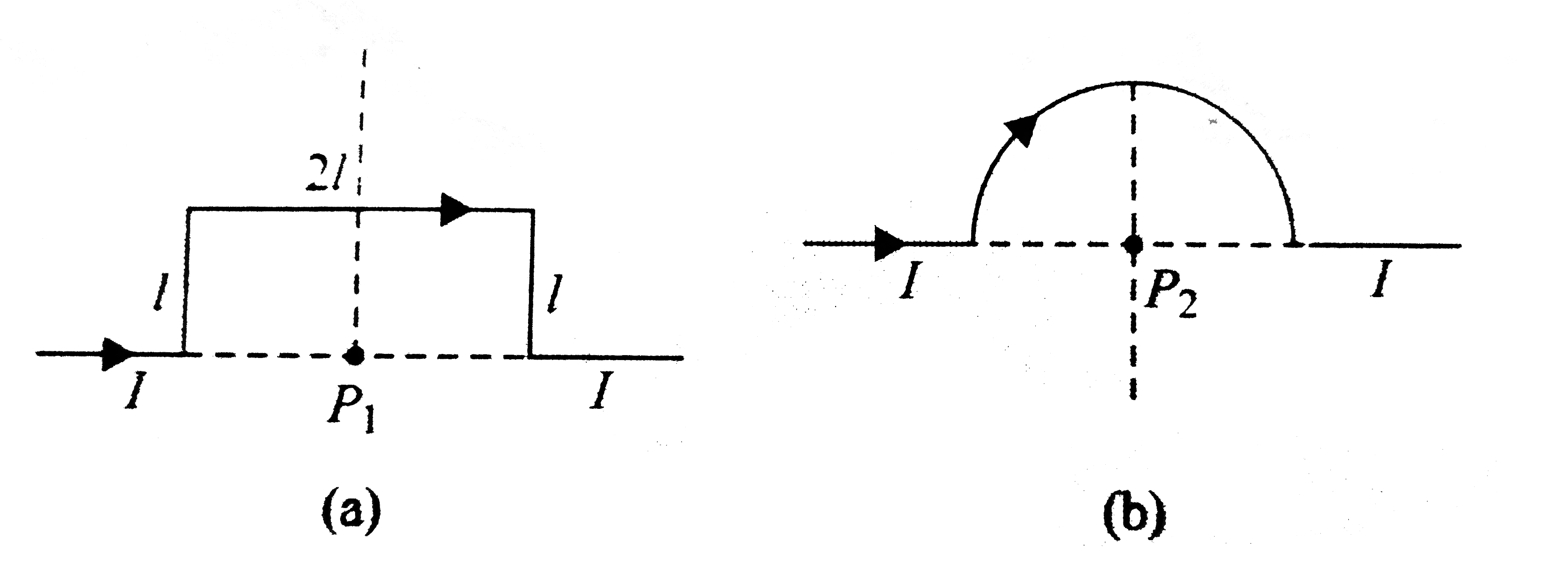

View SolutionCharge is sprayed onto a large non-conducting belt above the left-hand roller in Fig. The belt carries the charge, with a uniform surface charge density s, as it moves with a speed v between the rollers as shown in the figure. The charge is removed by a wiper at the right-hand roller. Consider a point just above the surface on the moving belt. Find an expression for the magnitude of magnetic field at this point.

View SolutionAn infinitely long, noc-conducting cylidner of radius R lies along the z-axis. Five long, conducting wires are parallel to the cylinder and spaced equally on the upperhalf of its surface. Each wire carries a current I in the opposite z-direction. Find the magnetic field on the z-axis. opposite z-direction. Find the magnetic field on the z-axis.
View SolutionIn Fig, find the magnetic field at point P. The loop is lying in x-y plane.

View SolutionTwo long, straight wires, one above the other, are separated by a distance 2a and are parallel to the x-axis. Let the y-axis be in the plane of the wires in the direction form the lower wire to the upper wire. Each wire carries current I in the +x-direction. What are the magnitude and direction of the net magnetic field of the two wires at a point in the plane of wires:
(a) midway between them?
(b) at a distance a above the upper wire?
(c) at a distance a below the lower wire?
View SolutionA long straight wire along the Z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coodinates (x, y) in the z = 0 plane is
View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of `R,I_1 and I_2`.

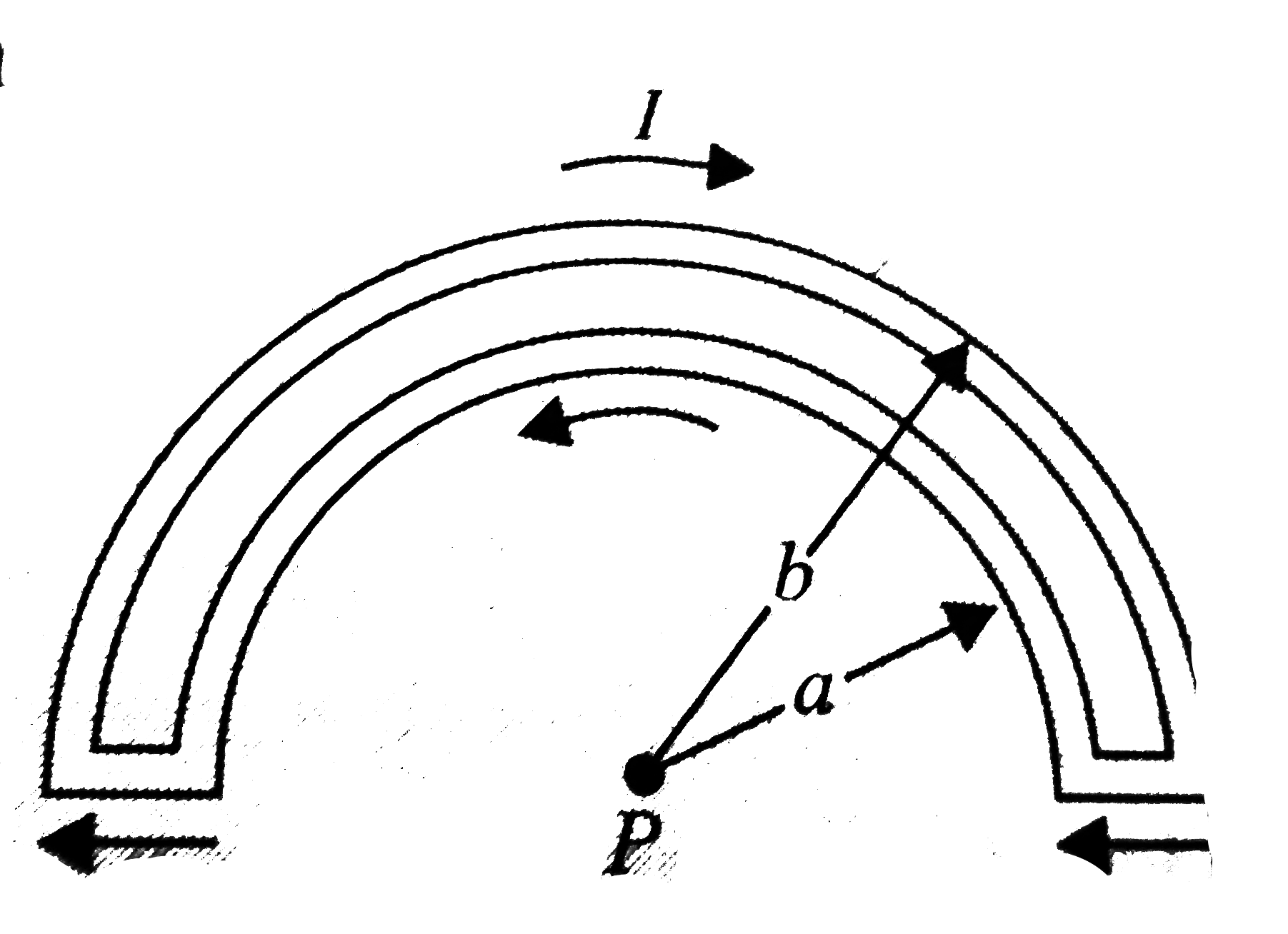
View SolutionTwo semicircles shown in Fig. have radii a and b. Calculate the net magnetic field (magnitude and direction) that the current in the wires produces at point P.
View SolutionA `+6muC` point charge is moving at a constant velocity of `8xx10^6 ms^-1` in the +y direction, relative to a reference frame. At the instant when the point charge is at the origin of this reference frame, what is the magnetic field vector it produces at the following points?
(a) `x=0.500m, y=0, z=0,` and (b) `x=0, y=-0.500m, z=0`.
View Solution
Concept Exercise 2.1 questions and complete solutions for chapter SOURCES OF MAGNETIC FIELD of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS SOURCES OF MAGNETIC FIELD
- Archives (fill In The Blanks)
- Archives (integer)
- Archives (linked Comprehension)
- Archives (multiple Correct )
- Archives (single Correct Anser)
- Concept Exercise 2.1
- Concept Exercise 2.2
- Exercise (assertion-reasioning )
- Exercise (integer)
- Exercise (linked Comprehension)
- Exercise (multiple Currect )
- Exercise (single Correct )
- Exercise (subjective )
- Illustration
- single correct Ansewer type
- single correct Answer Type
- Solved Example
- Subjective type