Complete Solutions to Exercise (linked Comprehension) of chapter SOURCES OF MAGNETIC FIELD of Class 12 book with complete answers and questions

There exists a long conductor along z-axis carrying a current `I_0` along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference `V_(BA)=V` is applied. Radii of arcs are a and b, respectively, as shown in the figure.

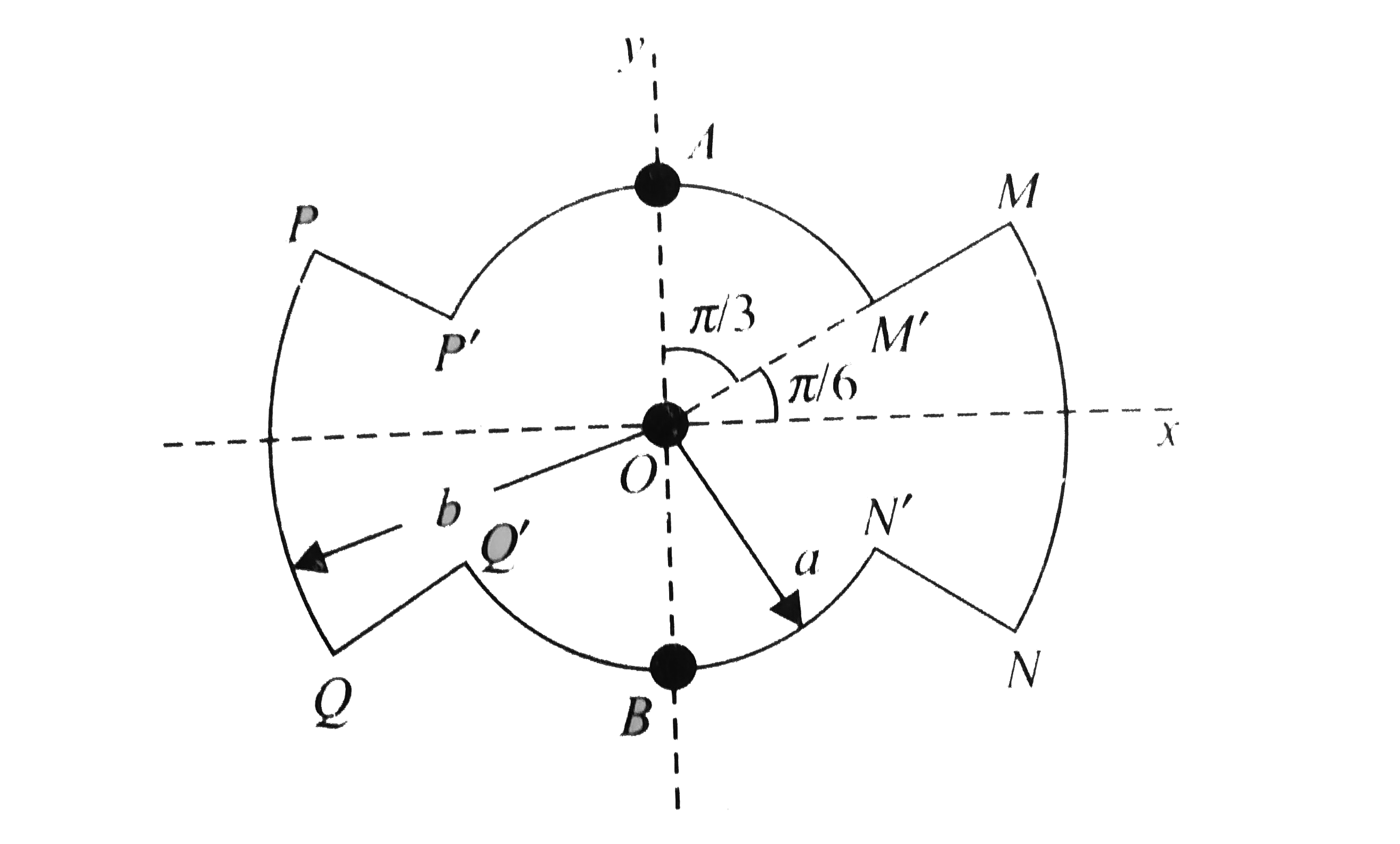
The magnitude of force experienced by the arc MN is

There exists a long conductor along z-axis carrying a current `I_0` along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference `V_(BA)=V` is applied. Radii of arcs are a and b, respectively, as shown in the figure.

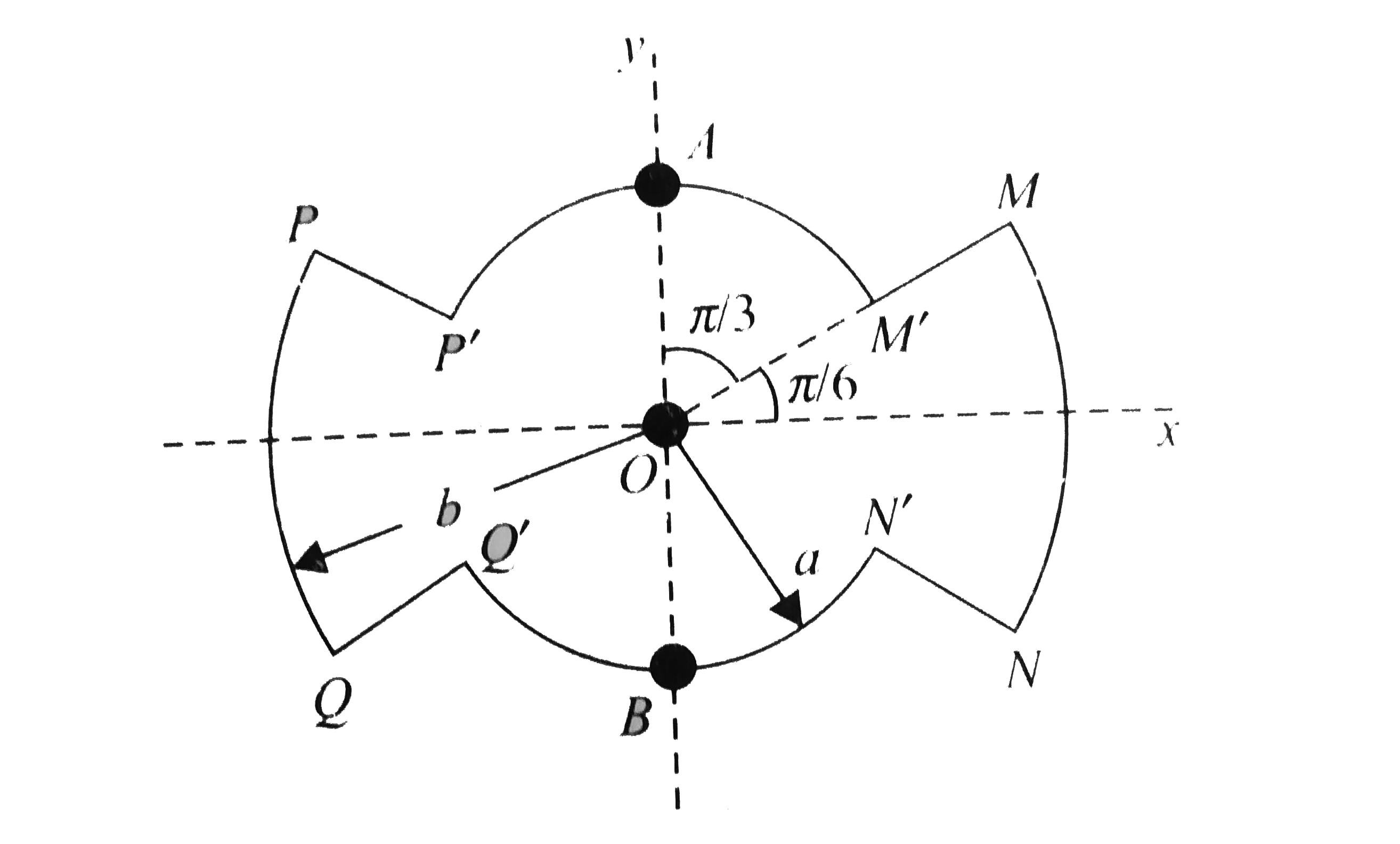
The total torque acting on the loop is nearly

Curves in the graph shown in Fig. give, as function of radius distance r, the magnitude B of the magnetic field inside and outside four long wire a,b,c and d, carrying currents that are uniformly distributed across the cross sections of the wires. Overlapping portions of the plots are indicated by double labels.

Which wire has the greatest radius?

Curves in the graph shown in Fig. give, as function of radius distance r, the magnitude B of the magnetic field inside and outside four long wire a,b,c and d, carrying currents that are uniformly distributed across the cross sections of the wires. Overlapping portions of the plots are indicated by double labels.

which wire has the greatest magnitude of the magnetic field on the surface?

Curves in the graph shown in Fig. give, as function of radius distance r, the magnitude B of the magnetic field inside and outside four long wire a,b,c and d, carrying currents that are uniformly distributed across the cross sections of the wires. Overlapping portions of the plots are indicated by double labels.

The current density in wire a is

Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is `ointvecB.dl=mu_0I_("in")`.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
Only the current inside the Amperian loop contributes in

Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is `ointvecB.dl=mu_0I_("in")`.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation `J=kr^2`, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.

Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is `ointvecB.dl=mu_0I_("in")`.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
In the above question, find the magnetic field induction at a point distance r from the axis when rgta. Assume relative permeability of the medium surrounding the conductor to be unity.

According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
`B=(mu_0I)/(4pir)(sinphi_1+sinphi_2)`
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given `OA=OB=OC=a`. Find the magnetic field at point B due to this loop.

According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
`B=(mu_0I)/(4pir)(sinphi_1+sinphi_2)`
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given `OA=OB=OC=a`. Find the magnetic field at point B due to this loop.

In Fig. the circular and the straight parts of the wire are made of same material but have different diameters. The magnetic field at the centre is zero.

Ratio of the currents `I_1 andI_2` flowing through the circular and straight parts is

In Fig. the circular and the straight parts of the wire are made of same material but have different diameters. The magnetic field at the centre is zero.

The ratio of the diameters of wires of circular and straight parts is

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current `I_1` of 6.00A into the plane of the paper.

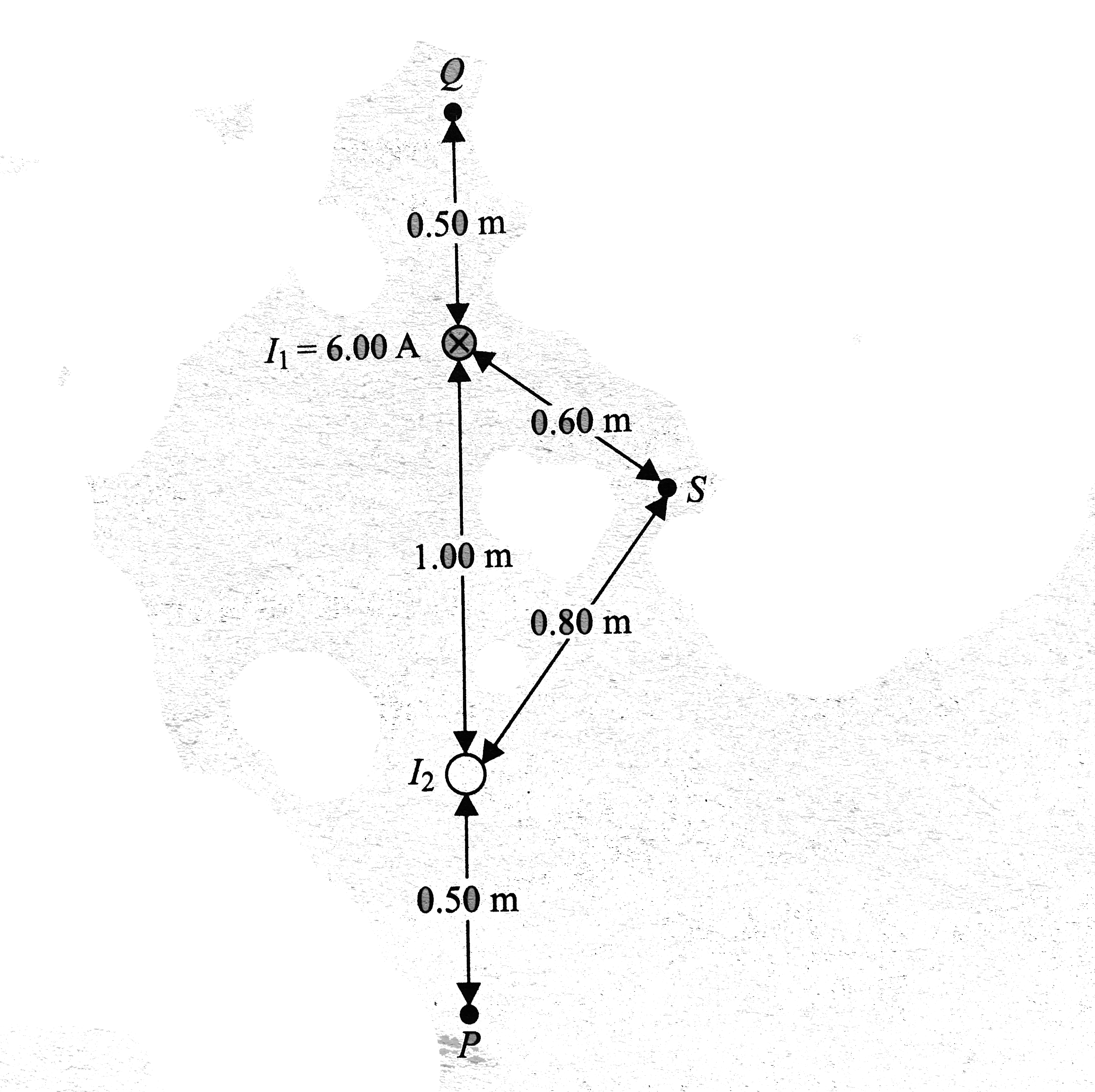
What must the magnitude of the current `I_2` be for the net field at point P to be zero?

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current `I_1` of 6.00A into the plane of the paper.

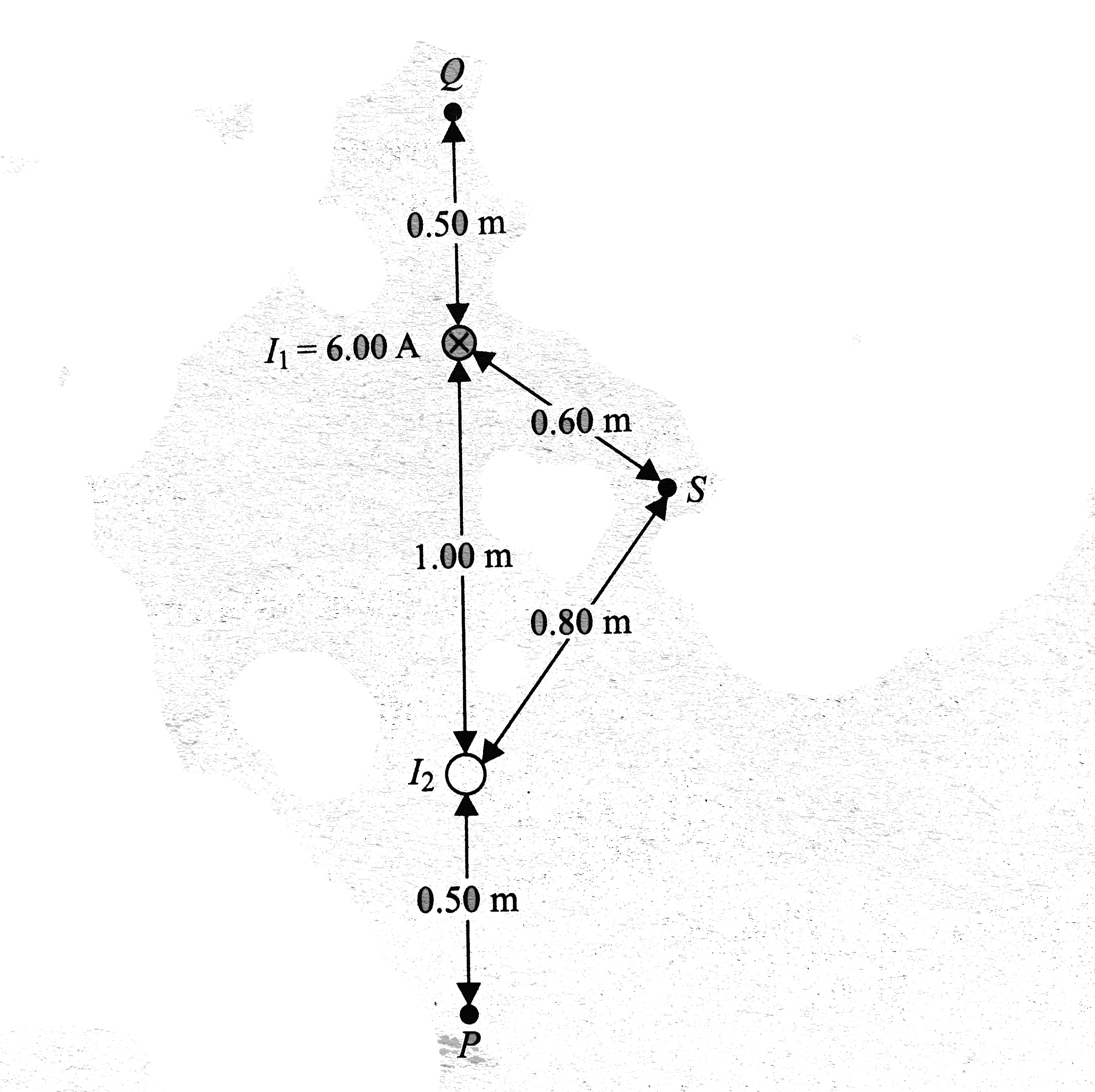
What is the magnitude of the net field at Q?

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current `I_1` of 6.00A into the plane of the paper.

What is the magnitude of the net field at S?

Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Derive an expression for the magnitude of `vecB` at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of `vecB`?

Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Graph the magnitude of `vecB` at point on the x-axis.

Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

At what value of x, the magnitude of `vecB` is maxismum?

Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Derive the expression for the magnitude of `vecB` at any point on the x-axis in terms of the x-coordinate of the point. What is the direciton of `vecB`?

Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Graph the magnitude of `vecB` at points on the x-axis.

Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
At what value of x is the magnitude of `vecB` is maximum?