Complete Solutions to Solved Example of chapter SOURCES OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCES OF MAGNETIC FIELD |
| CENGAGE PHYSICS | Solved Example |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
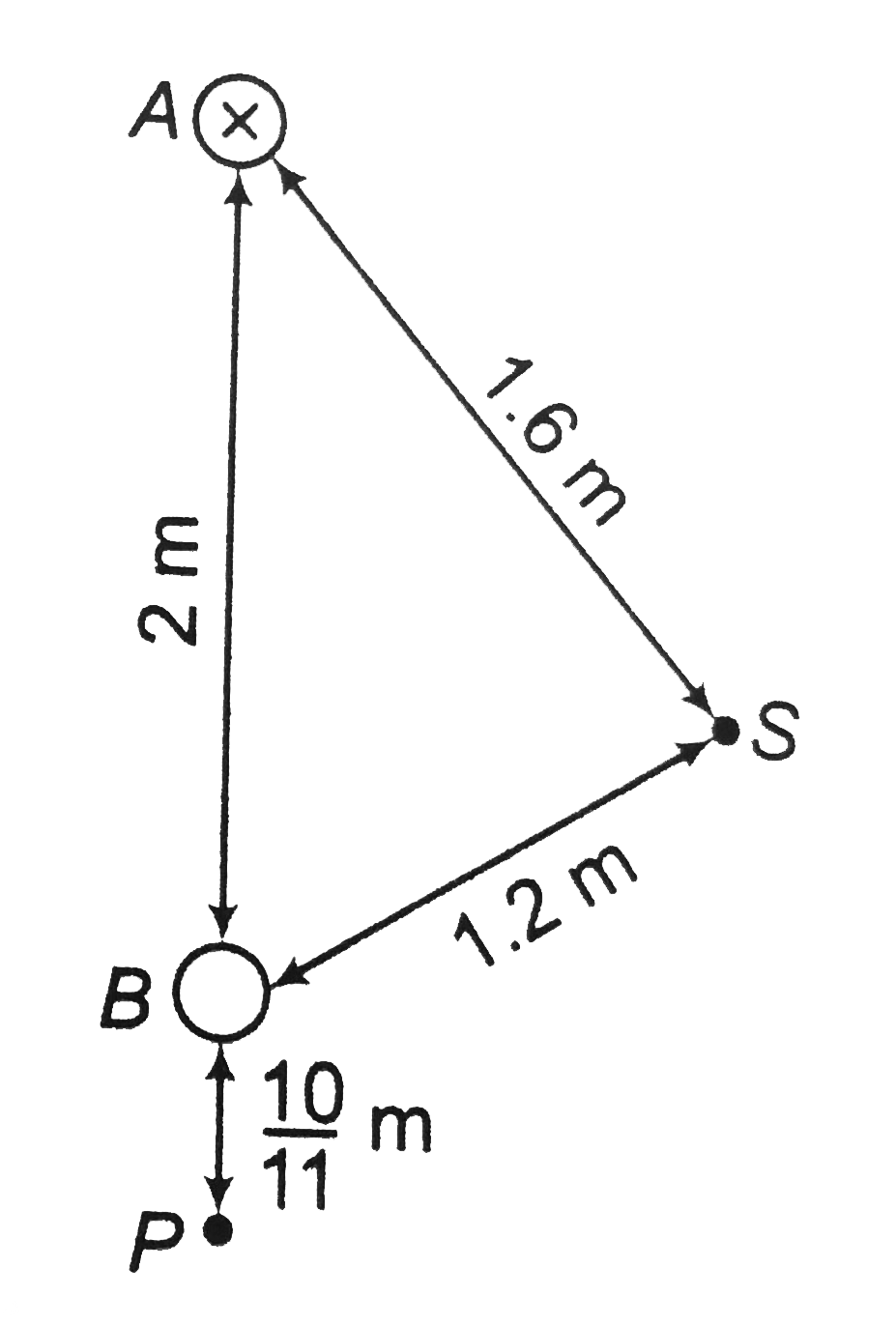
Two long straight parallel wieres are `2m` apart, perpendicular to the plane of the paper. The wire A carries a current of `9.6 A`, directed into the plane of the paper. The wire `B` carries a current such that the magnetic field of induction at the point `P`, at a distance of `10/11` m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont `S`.
c. the force per unit length on the wire `B`.
View SolutionTwo long parallel wires carrying current 2.5 A and I in the same direction (directed into plane of the paper 0 are held ar P and Q respectively,such that they are perpendicular to the plane of paper .The points O and Q are located at distance of 5 m and 2 m respectively,from a collinear point R
(i0 An electron moving with a velocity of `4xx10^(5)`m/s along positive x-direction experiences a force of magnitude `3.2xx10^(-20)` n at the point R.Find the value of i
(ii) Find all positions at which a third long parallel wire carrying a current of magnitude 2.5 A may be placed, so that magnetic field at R is zero
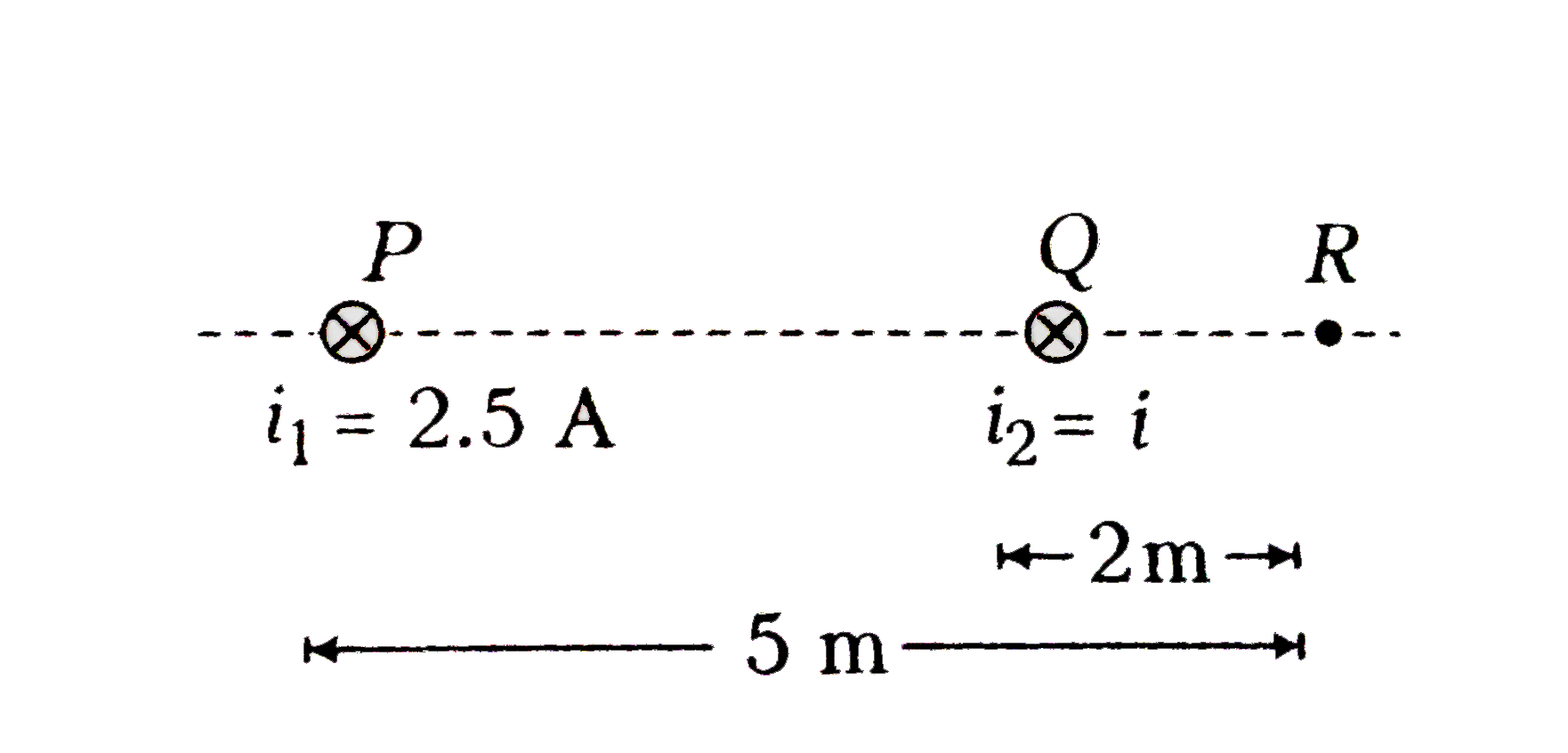
View SolutionA wire loop carrying a current `I` is placed in the `xy`-plane as shown in figure
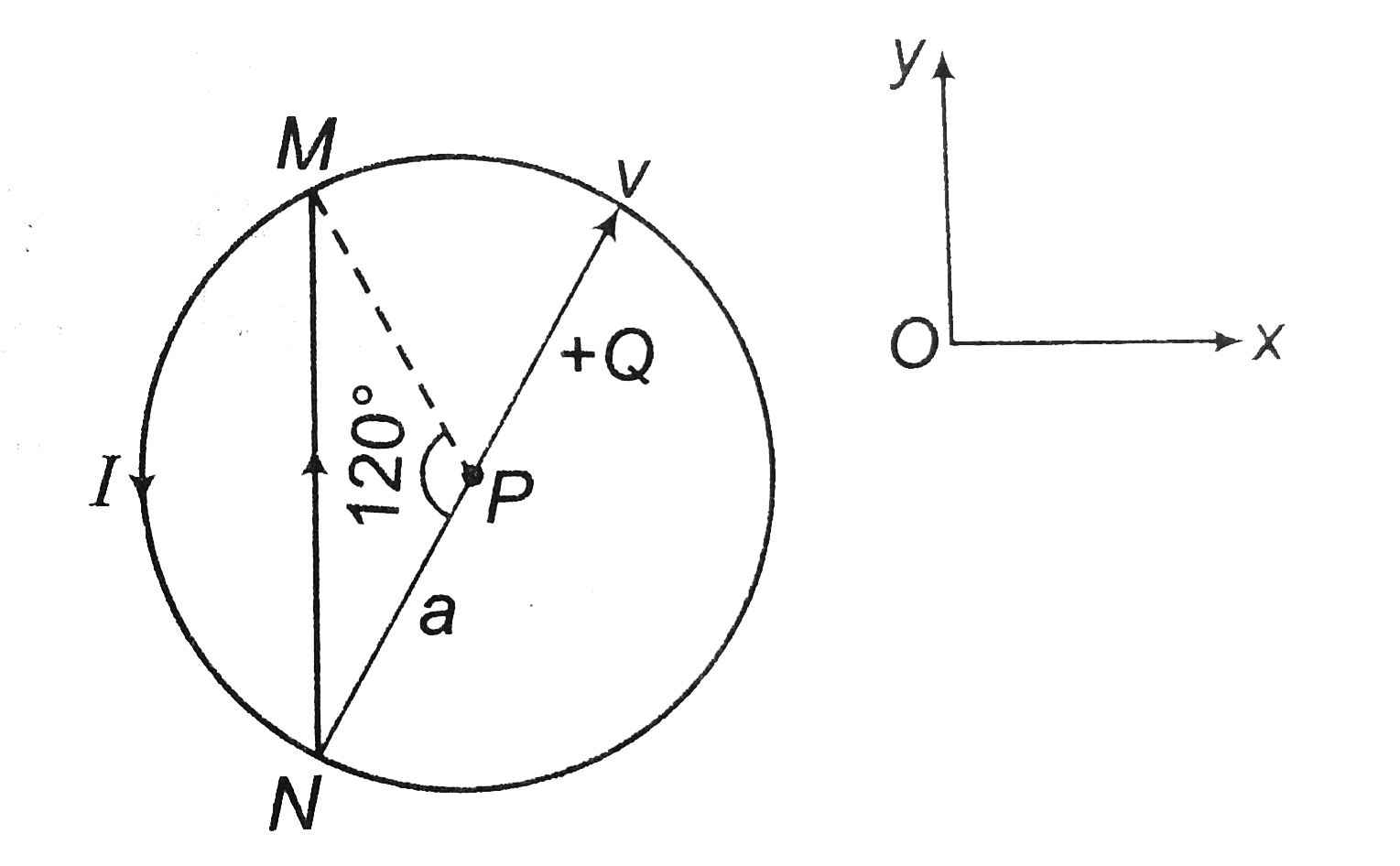
a. If a particle chsarge +Q and mass m is placed at in centre `P` and given a velocity `v` along `NP` (see figure), find its instaneous acceleration.
If an external uniform magnetic induction field `B=Bhati` is applied, find the force and the torque acting on the loop due to this field.
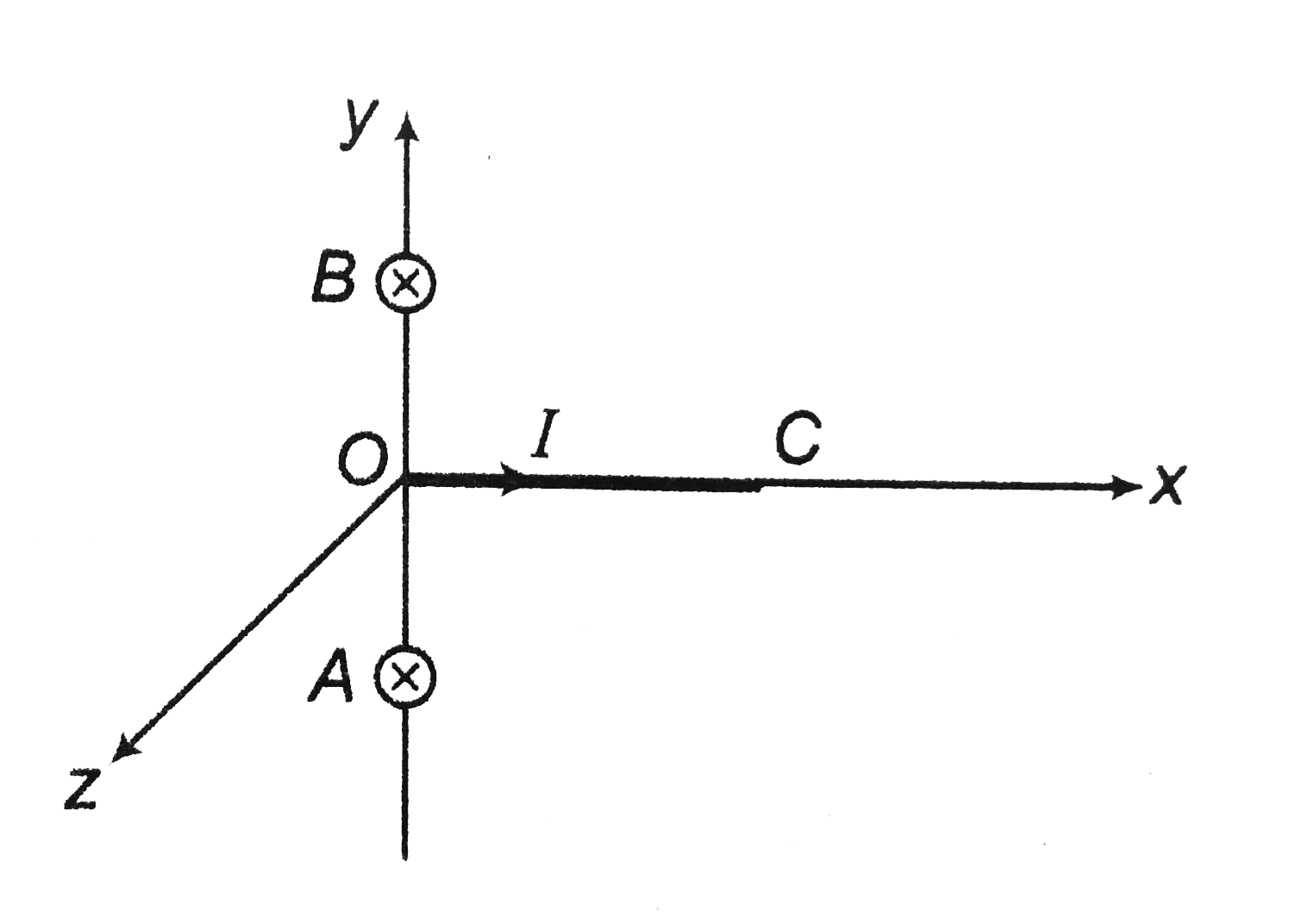
View SolutionA straight segment `OC` (of lengh `L`) of a circuit carrying a current I is placed along the x-axis. Two infinitely long straight wire `A` and `B` each extending from `z=-ooto+oo` are fixed at `y=-a` and `y=+a` respectively as show in the figure. If the wires `A` and `B` each carry a current I into the plane of the paper, obtain the expression for the force acting on the segment `OC`. What will be the force on `OC` if the current in the wire `B` is reversed?
View SolutionA long horizontal wire `AB`,which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another paralllel long wire `CD` which is fixed in a horizontal plane and carries a steady current of `30 A`, as shown in figure. Show that when `AB` is slightly
depressed it executes simple harmonic motion. Find the period of oscillations.

View SolutionThree infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along `x=+-d`
i find the locus of the points for which the magnetic field `B` is zero.
ii If the central wire is displaced along the `z`-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is `lamda`, find the frequency of oscillation.
View SolutionA pair of stationary and infintely long bent wires are placed in the ` XY` planes as shown in fig. The wires carry currents of ` I = 10 amperes` each as shown . The segments `P and Q` are parallel to the ` Y-axis` such that ` OS = OR = 0.02 m`. Find the magnitude and direction of the magnetic induction at the origin `O`.
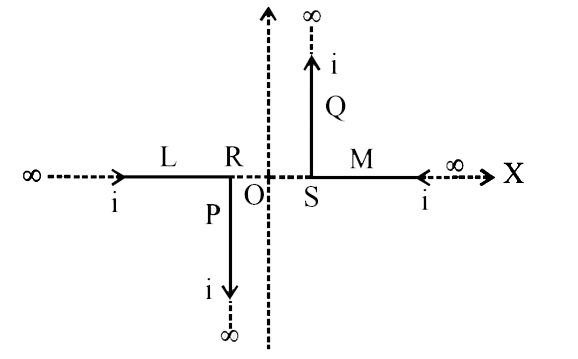
View SolutionA current of `10 A` flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii `r_1=0.08m` and `r_2 =0.12m`. Each subtends the same angle at the centre.
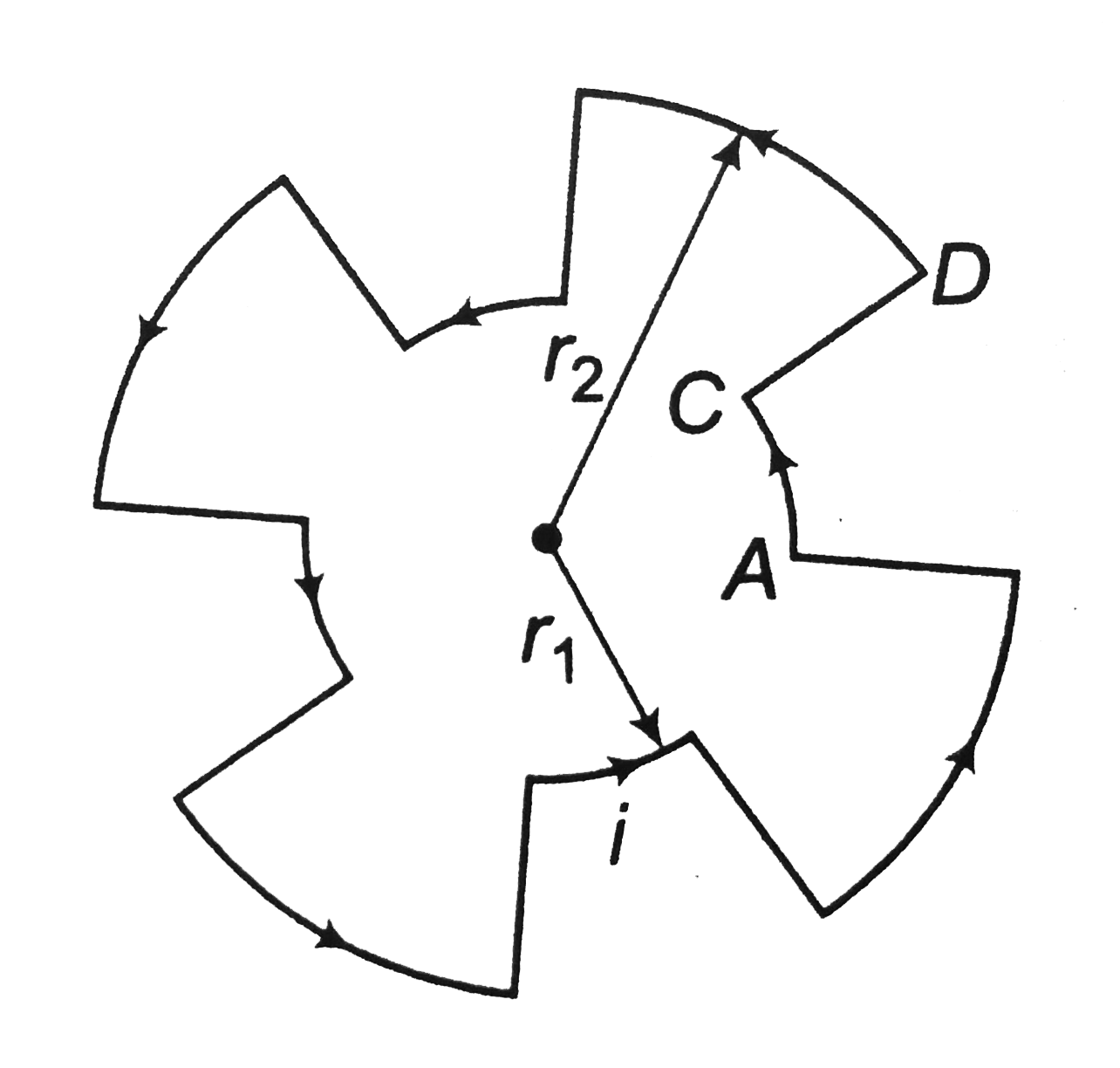
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of `10 A` is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc `AC` and the straight segment `CD` due to the current at the centre?
View SolutionA circular loop of radius `R` is bent along a diameter and given a shapes as shown in the figure. One of the semicircles `(KNM)` lies in the ` x-z` plane with their centres and the other one `(KLM)` in the `y-z` plane with their centres at the origin. current `I` is flowing through each of the semi circles as shown in figure.
(a) A particle of charge `q` is released at the origin with a velocity `vec(v) = -v_(0)hat(i)`. Find the instantaneous force `vec(F)` on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field `B_(0) hat(j) ` is applied , determine the force `vec(F)_(1) and vec(F)_(2)` on the semicircles `KLM and KNM` due to the field and the net force ` vec(F)` on the loop.
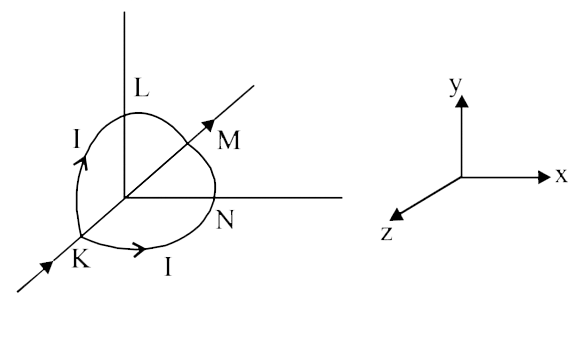
View SolutionCenters of two similar coils P and Q having same number of turns are located at the coordinates (0.4,0) and (0,0.3) such that the plane of coils are perpendicular to X-and Y-axis respectively. The areas of cross section of coils P and Q are in the ration `4:3` Coil P has 16 A current in clockwise direction and coil Q has `9sqrt3A` current in anticlockwise direction as seen from the origin. A small compass needle is placed at the origin. Find the deflection in the needle, assuming the earth's magnetic field negligible and the radii of the coils very small compared to their distances from the origin.
View SolutionA coil of radius R carries current `i_1`. Another concentric coil of radius `r(rlt ltR)` carries current `i_2`. Planes of two coils are mutually perpendicular and both the coil are free to rotate about common diametre. Find maximum kinetic energy of smaller coil when both the coils are released, masses of coils are M and m, respectively.
View SolutionA current I flows along a round loop. Find the integral `intvecB.vec(dr)` along the axis of the loop within the range from `(-oo)` to `(+oo)`. Explain the result obtained.
View SolutionInside a long straight uniform wire of round cross- section there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from latter by a distance d. If a direct current of density `vecj` flows along the wire, then magnetic field inside the cavity will be
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity `omega`. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA sphere of radius R, uniformly charged with the surface charge density `sigma` rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.
View SolutionA long straight wire is coplanar with a current carrying circular loop of radius R as shown in Fig. Current flowing through wire and the loop is `I_0` and I, respectively. If distance between centre of loop and wire is `r=2R,` calculate force of attraction between the wire and the loop.

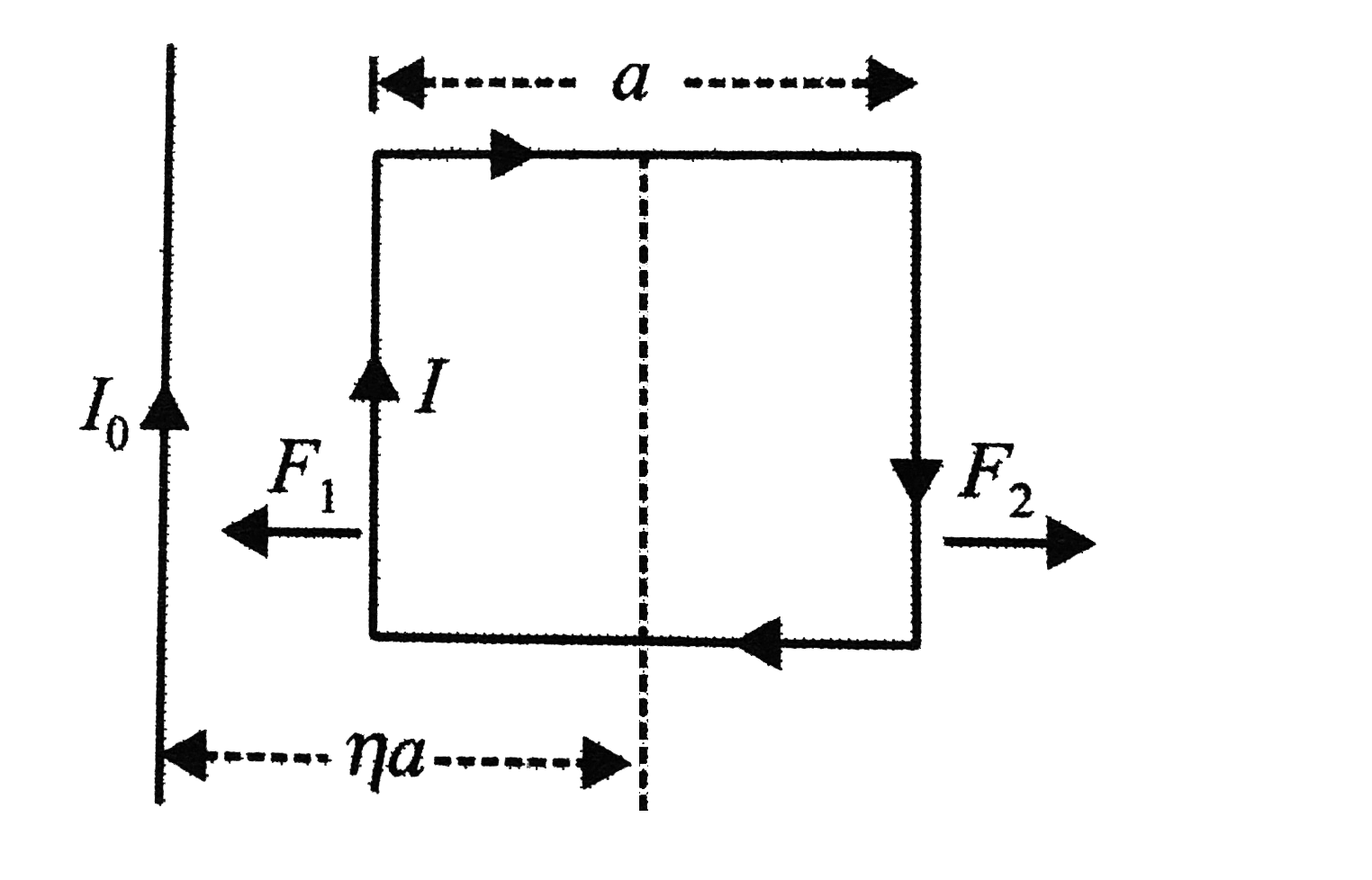
View SolutionA square frame carrying a current `I=0.90A` is located in the same plane as a long straight wire carrying a current `I_0=5A`, The frame side has a length `a=8cm`. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance `h=15` times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through `180^@` about its axis, with the current maintained constant.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance `x_0` from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
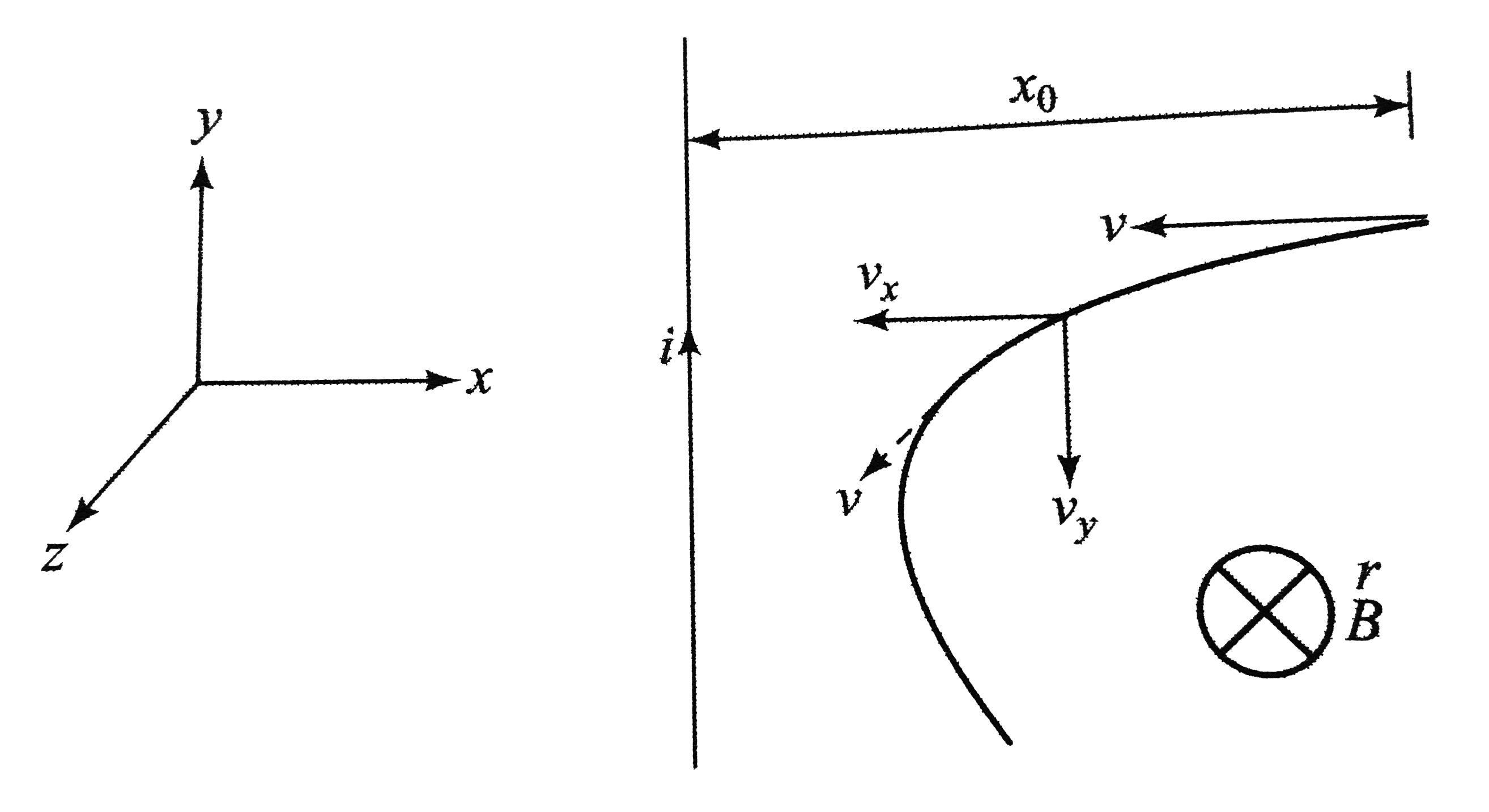

View SolutionFrom the surface of a round wire of radius a carrying a direct current i, a positive charge q escapes with a velocity `v_0` perpendicular to the surface. Find what the maximum distance of the electron will be from the axis of the wire before it turns back due to the action of the magnetic field generated by the current.
View Solution
Solved Example questions and complete solutions for chapter SOURCES OF MAGNETIC FIELD of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS SOURCES OF MAGNETIC FIELD
- Archives (fill In The Blanks)
- Archives (integer)
- Archives (linked Comprehension)
- Archives (multiple Correct )
- Archives (single Correct Anser)
- Concept Exercise 2.1
- Concept Exercise 2.2
- Exercise (assertion-reasioning )
- Exercise (integer)
- Exercise (linked Comprehension)
- Exercise (multiple Currect )
- Exercise (single Correct )
- Exercise (subjective )
- Illustration
- single correct Ansewer type
- single correct Answer Type
- Solved Example
- Subjective type