Complete Solutions to Subjective of chapter COULOMB LAW AND ELECTRIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | COULOMB LAW AND ELECTRIC FIELD |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Suppose that `1.0g` fo hydrogen is separated into electrons and protons. Suppose also that the protons are palced at the earth's north pole and the electrons are placed at the south pole. What is the resulting compression force on earth? (Given that the radius of rarth is 6400 km).
View SolutionTwo identical conducting small spheres are placed with their centers 0.3 m aparts. One is given a charge of 12.0 nC and the other a charge of `-18.0 nC`.
(a) Find the electric force exerted by one sphere on the other?
(b) If the spheres are connected by a conducting wire, find the electric force between the two after they attain equilibrium.
View SolutionFour equal point charges, each of magnitude `+Q`, are to be placed in equilibrium at the corners of a square. What should be the magnitude and sign of the point charge that should be placed at the center of the square to do this job?
View SolutionTwo point electric charges of value `q` and `2q` are kept at a distance `d` apart from each other in air. A third charge `Q` is to be kept along the same line in such a way that the net force action on `q` and `2q` is zero. Calculate the position of charge `Q` in terms of `q` and `d`.
View SolutionTwo fixed point charges `+4e` and `+e` units are separated by a distance a. Where should a third point charge be placed for it to be in equilibrium?
View SolutionTwo identical particles are charged and held at a distance of 1m form each pther. They are found to be attraction each other with a force of 0.027N . Now they are connected by a conducting wire so that charge folws between them. Whe the charge flow stop, they are found to be repelling each other with a force of 0.009N. Find the initial charge on each particle.
View SolutionTwo similarly and equally charged identical metal spheres A and B repel each other with a force of `2xx10^(-5)N`. A third identical unchared sphere C is touched with A and then placed at the midpoint between A and B. Find the net electric force on C.
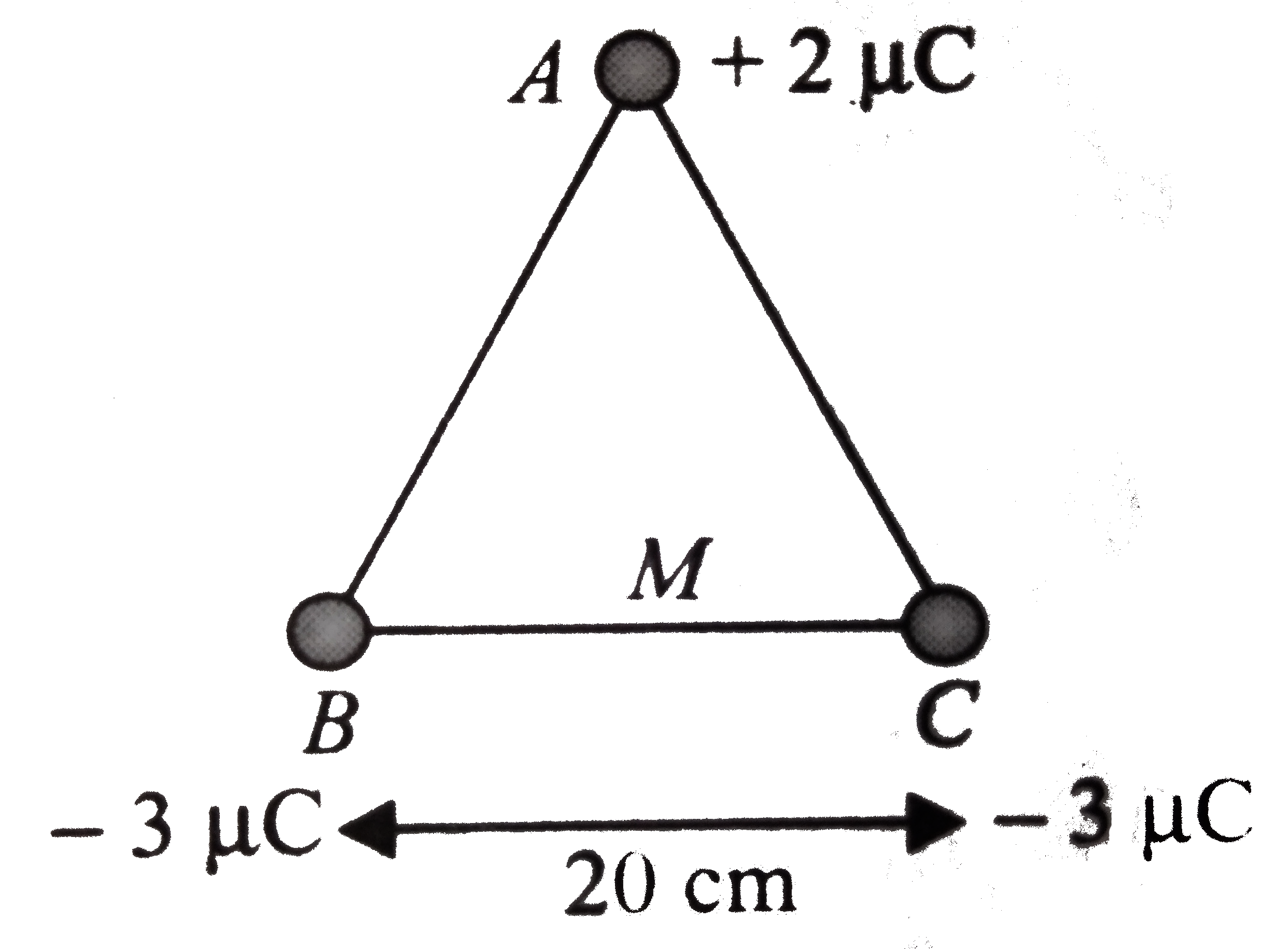
View SolutionThree point charges of `+2muC, -3muC` , and `-3muC` are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
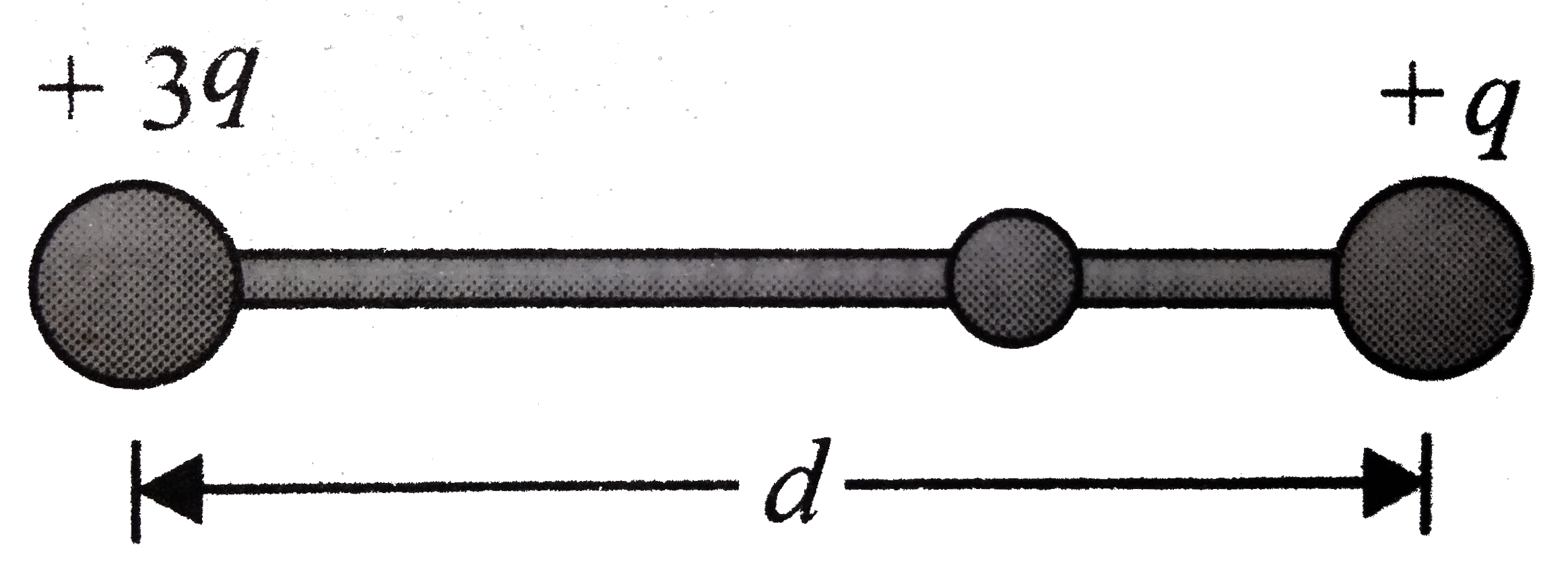
View SolutionTwo small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origein to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable eqyilibrium ?
View SolutionA copper atom consists of copper nucles surrounded by 29 electrons. The atomic weight of copper is `63.5 gmol^(-1)`. Let us now take two poeces of copper each weighing 10g. Let one electrof from one piece be transferred to another for every 1000 atom in a piece. ltbRgt (a) Find the magnitude of charge appearing on each piece.
(b) What will be the Coulomb force between the two poeces after the transfer of electrons if they are 10cm apart?
View SolutionA flat square sheet of charge (side 50 cm) carries a uniform surface charge density. An electrons0.5 cm form a point near the center of the sheet experiences a force of `1.8xx10^(-12)N` directed away from the sheet. Determine the total charge on the sheet.
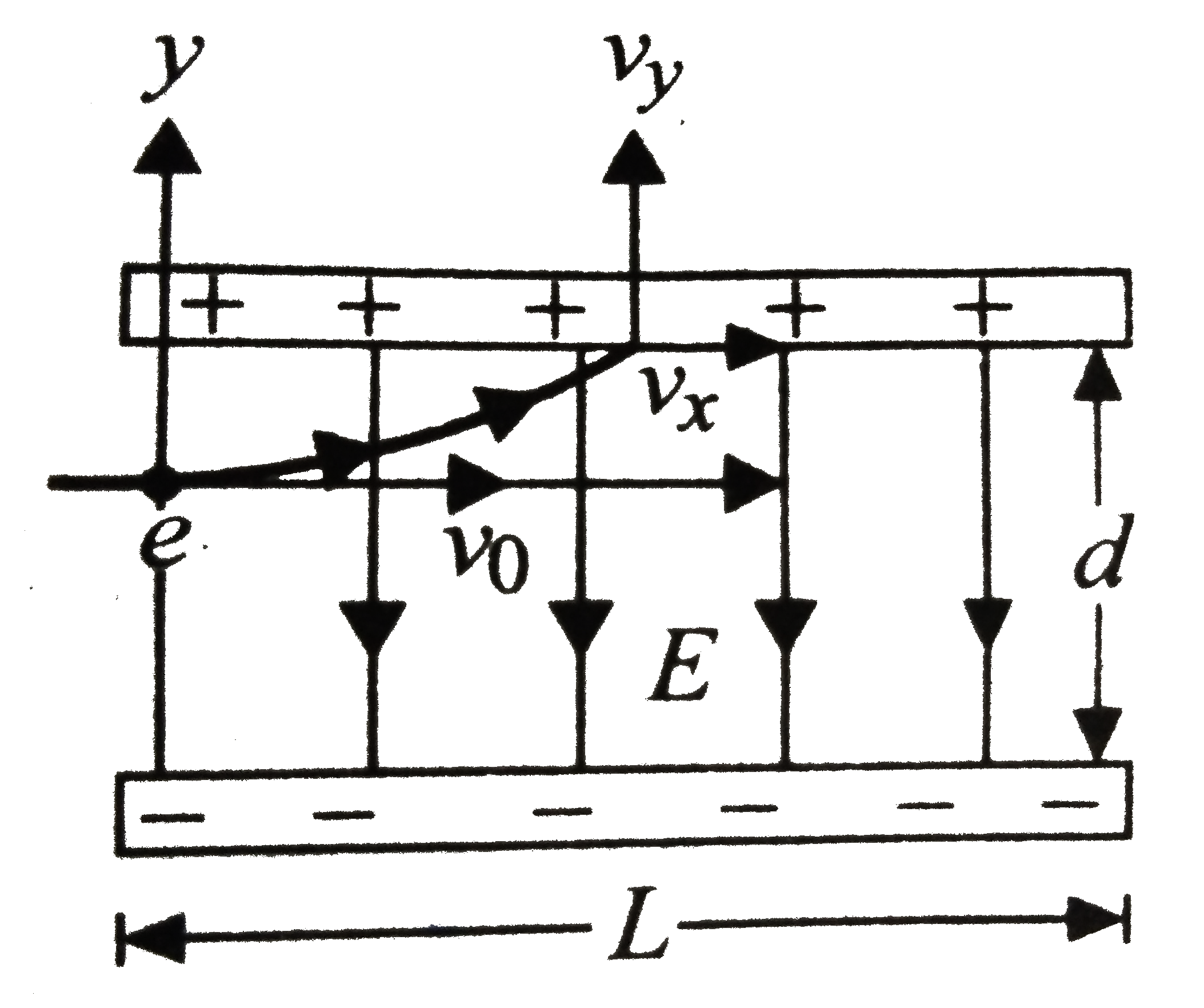
View SolutionA particle of mass `9xx10^(-31)` kg having a negative charge of `1.6xx10^(-19)C` is projected horizontally with a velocity of `10^(6)ms^(-1)` into a region between two infinite horizontal parallel plates of metal. The distance between the plates is `d=0.3cm` and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of hte velocity of hte paricle just before it hits one of the plates.
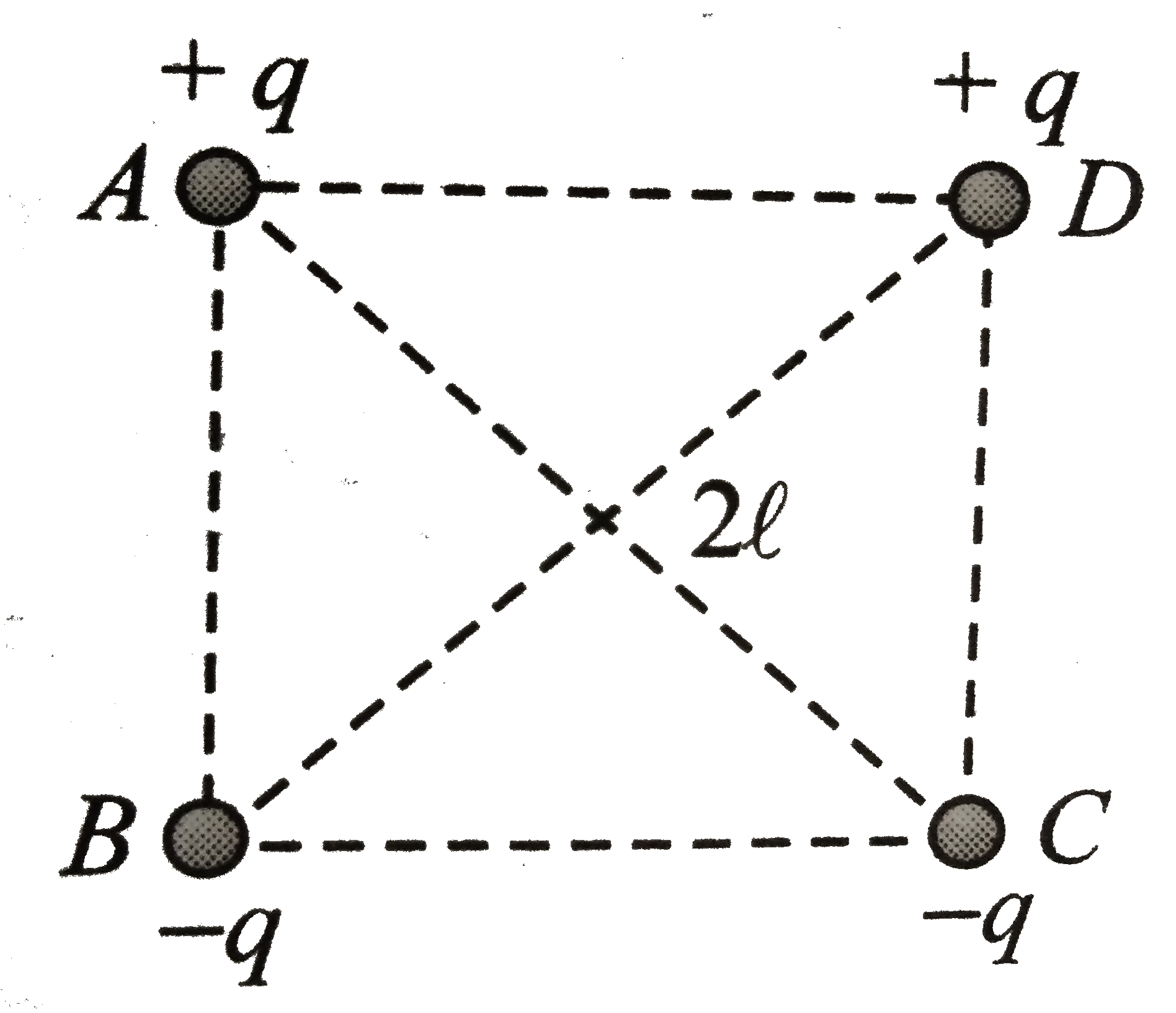
View SolutionPoint chages q and -q are located at the verticles of a squre with diagonals 2l as shown in fig. Evaluate the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of the square at a distanc x from the center.
View SolutionTwo mutually perpendicular long straight conductors carrying uniformly distributed charges of linear charges densities `lambda_(1)` and `lambda_(2)` are positon at a distance a from each other. How does the interaction between the rods depends on a ?

View SolutionA ring of radius 0.1m is made out of thin metallic wire of area of cross section `10^(-6)m^(2)`. The ring has a uniform charge of `pi` coulombs. Find the change in the radius of the rig when a charge of `10^(-8)C` is placed at the center of the ring. Young's modulus of hte metal is `2xx10^(11)Nm^(-2)`.
View SolutionA charged cork ball of mass m is suspended on a light sting in the presence of a uniform electric field as shown in fig. When `E=(A hat i+B hat j)NC^(-1)`, Where A and B positive numbers, the ball is in equilibirum at `theta`. Find (a) the charge on the ball and (b) the tension in the string.
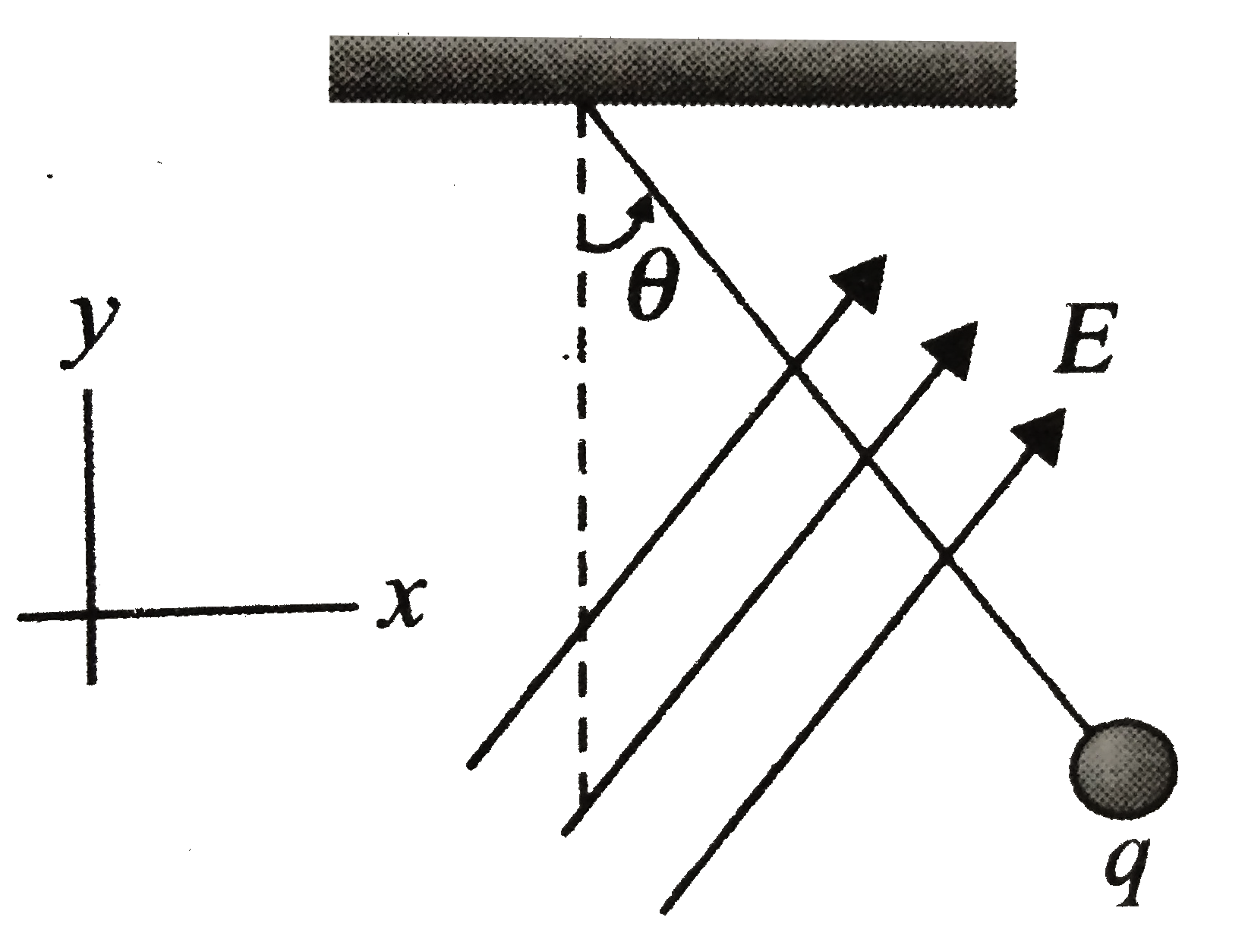
View SolutionA ring of radius R has charge `-Q` distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionTwo identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibirum whaen th distance between them is a(the length of thread `Lgtgta`). Then one of the balls is discharged. what will be the distance `b(bltltL)` between the balls when equilibrium is restored?
View SolutionTwo point charge `Q_(a)` and `Q_(b)` are positional at point A and B. The field strenght to the right of charge `Q_(b)` on the line that passes therough the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincedes with the positive direction of the x-axis. The distance between the charges is `l=21 cm`.
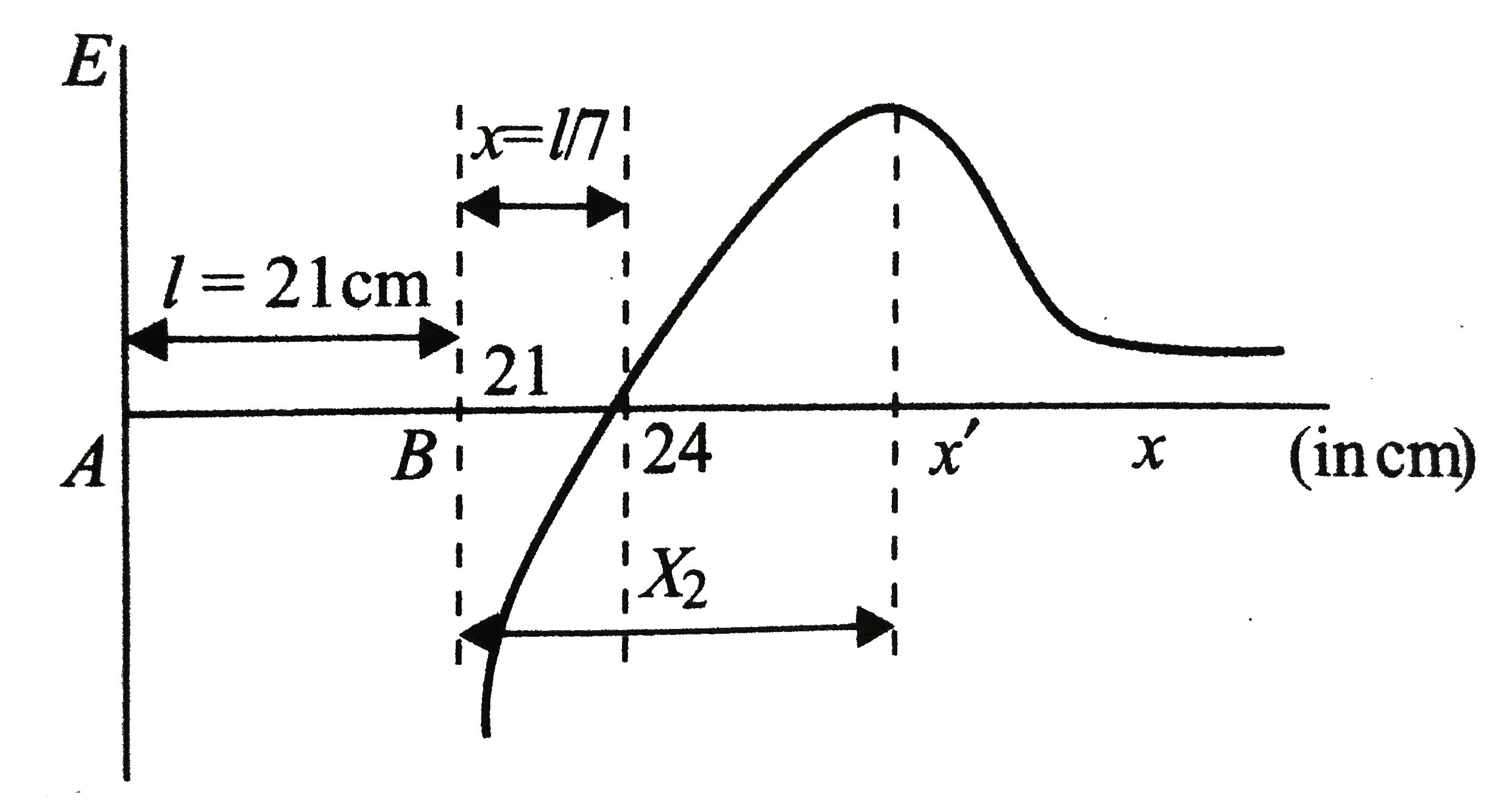
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge `Q_(a)` and `Q_(b)`.
(c ) Find the coordinate x of the point where the field strenght is maximum.
View SolutionTwo semicircle wires ABC, and ADC, each of radius R are lying on xy and xz planes, respectively as shown in fig.
if the linear charge density of the semicircle parts and straight parts and straight parts is `lambda`, Find the electric field entensity `vec(E)` at the origin .

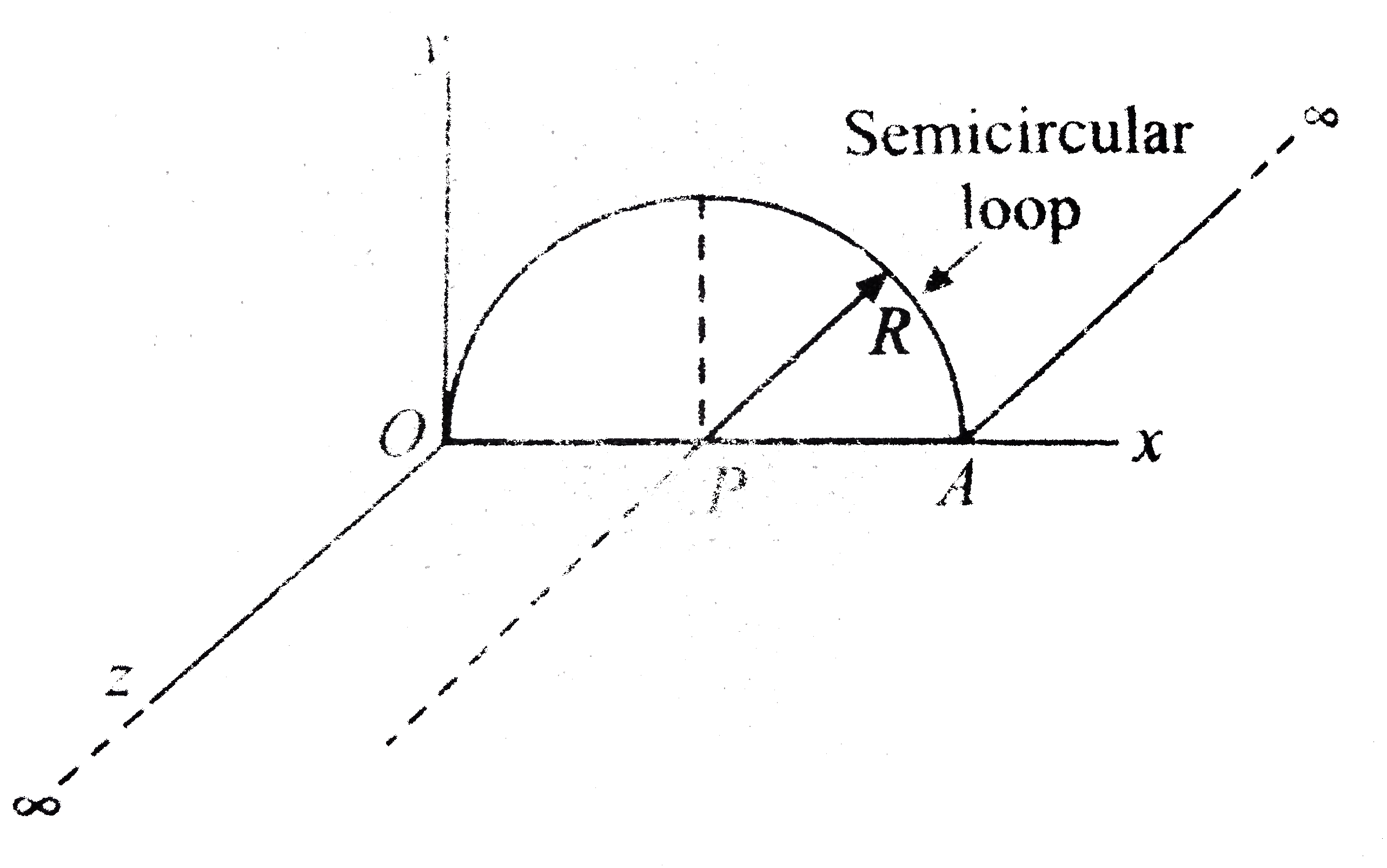
View SolutionAn infinte wire having linear charge density `lambda` is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
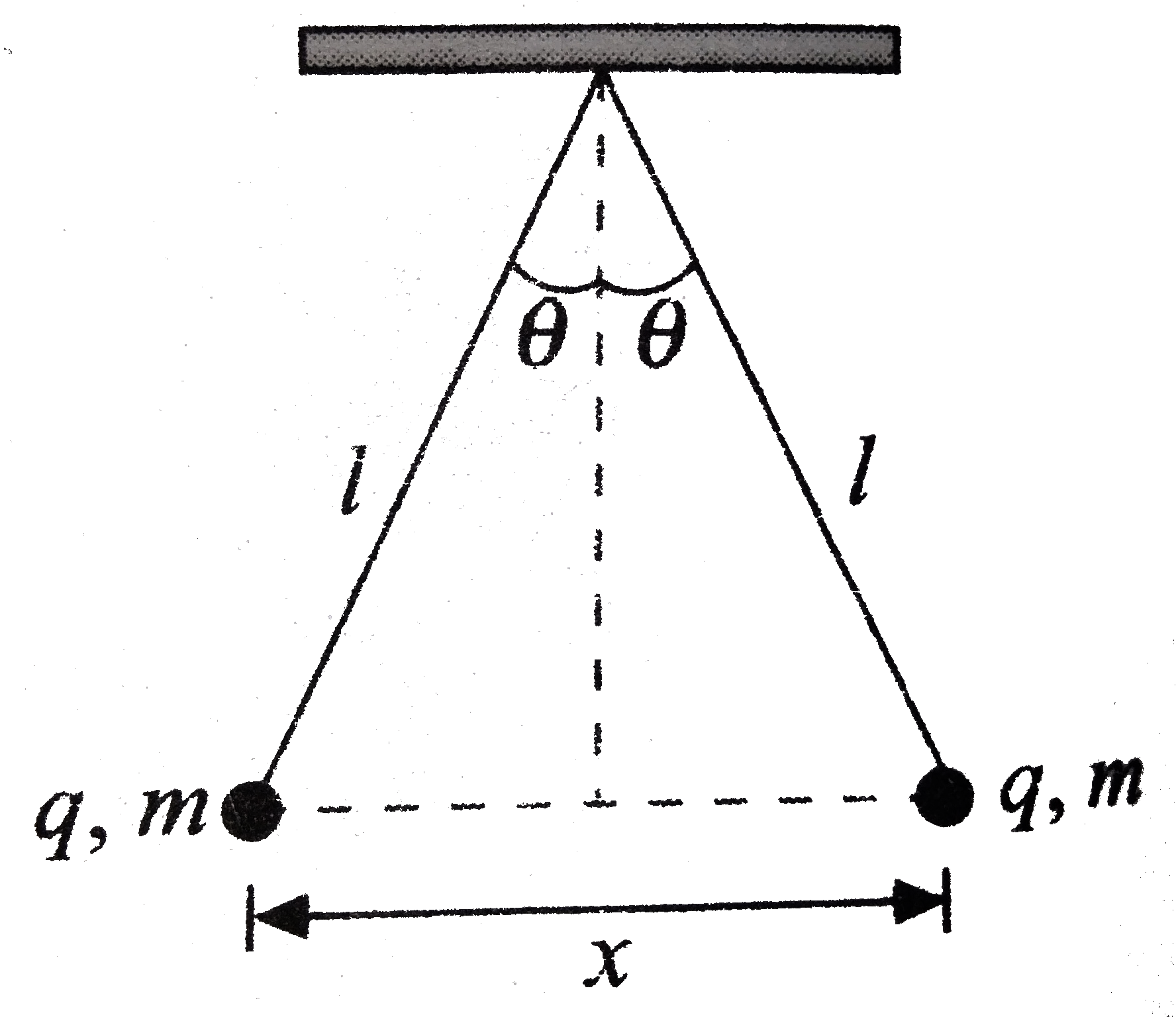
View SolutionTwo similar balls, each of mass m and charge q, are hung from a common point by two slik threads, each of length l. Prove that separation between the ball is `x=[(q^(2)l)/(2 pi epsilon_(0)mg)]^(1//3)`, if `theta` is small
Find the rate `(dq)/(dt)` with which the charge should leak off each sphere if the velocity of approach varies as `v=a//sqrt(x)`, where a is a constant.
View SolutionThree equal negative charges, `-q_(1)` each form the vertices of and equilateral triangle . A particle of mass m and a positive charge `q_(2)` is constrained to move along a line perpendicular to the plane of triangle and through its center, which at a distance r from each of the negative charges as shown in fig. The whole systen is kept in gravity-free space, Find the tome period of vibration of the particle for small displacement from the equilibrium position.

View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as `rho=rho_(0)(1-r//R)`, Where `rho_(0)` is a constant and r is the distance of the point from the center. Assume the permittivies of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of hte distance r both inside and outside the ball.
(b) Find the maximum intensity `E_("max")` and the corresponding distance `r_(m)`.
View SolutionA uniform nonconducting rod of mass ma and length l, with charge density `lambda` as shown in fig. is hanged at the midpoint at orgin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists paralled to xaxis in th entire region. Calculated the period of small oscillation of the rod .

View SolutionElectrically charged drops of nercury fall from an altitude h into a sperical metal vessel of radius R. There is a small opening in the upperapart of the vessel. The mass of eanc drop is m, and the charge on the drop is Q. What will be the number n of the last drop taht can still enter the sphere?
View SolutionA thin rigid insulated rod of mass m and length l carrying a charge Q unformly distrivuted along its length is smoothly pivoted at P. It is palced in between the charged large conducting plates. Disregard gravity.
(a) Find the initial accelaeration of the rod.
(b) Find the angular speed of the rod as the function of angel `theta` of rotation `omega=f(theta)`, if the rod is allowed to rotate freely .

View SolutionTwo particles of chargaes and masses `(+q_(1),m_(1))` and `(+q_(2),m_(2))` are reelaesed at two different points in a uniform electric field E established in free space. If their separation remains unchanged find the separation l between them .
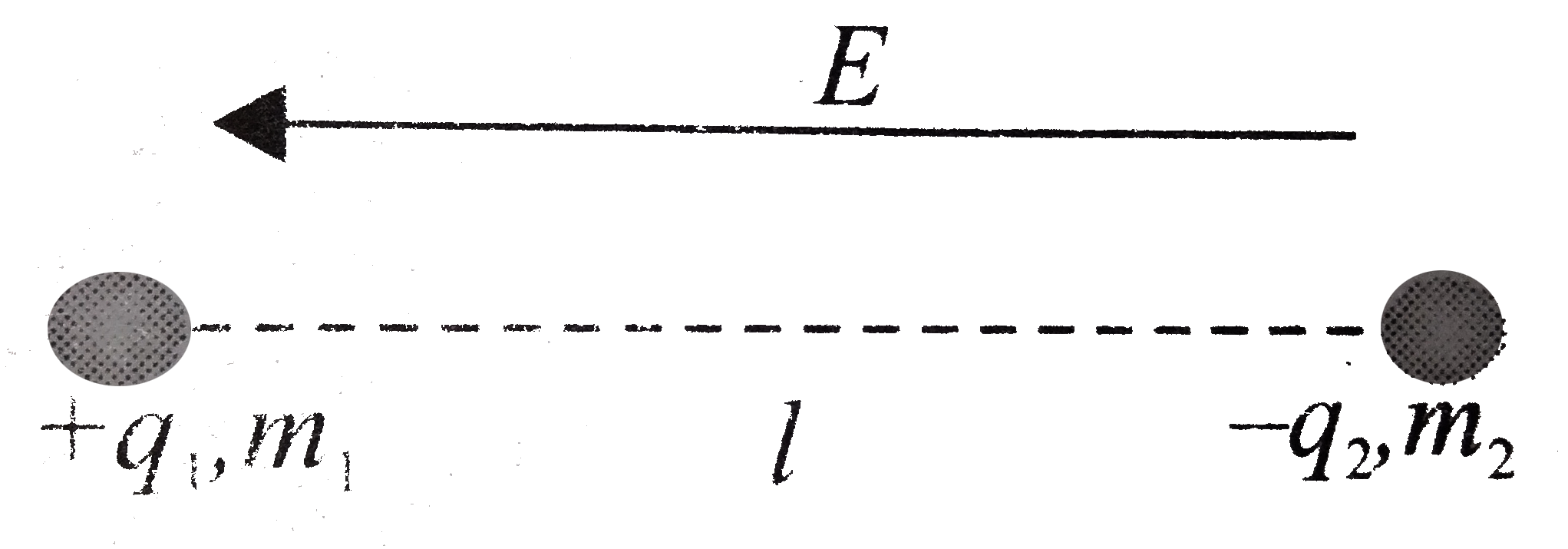
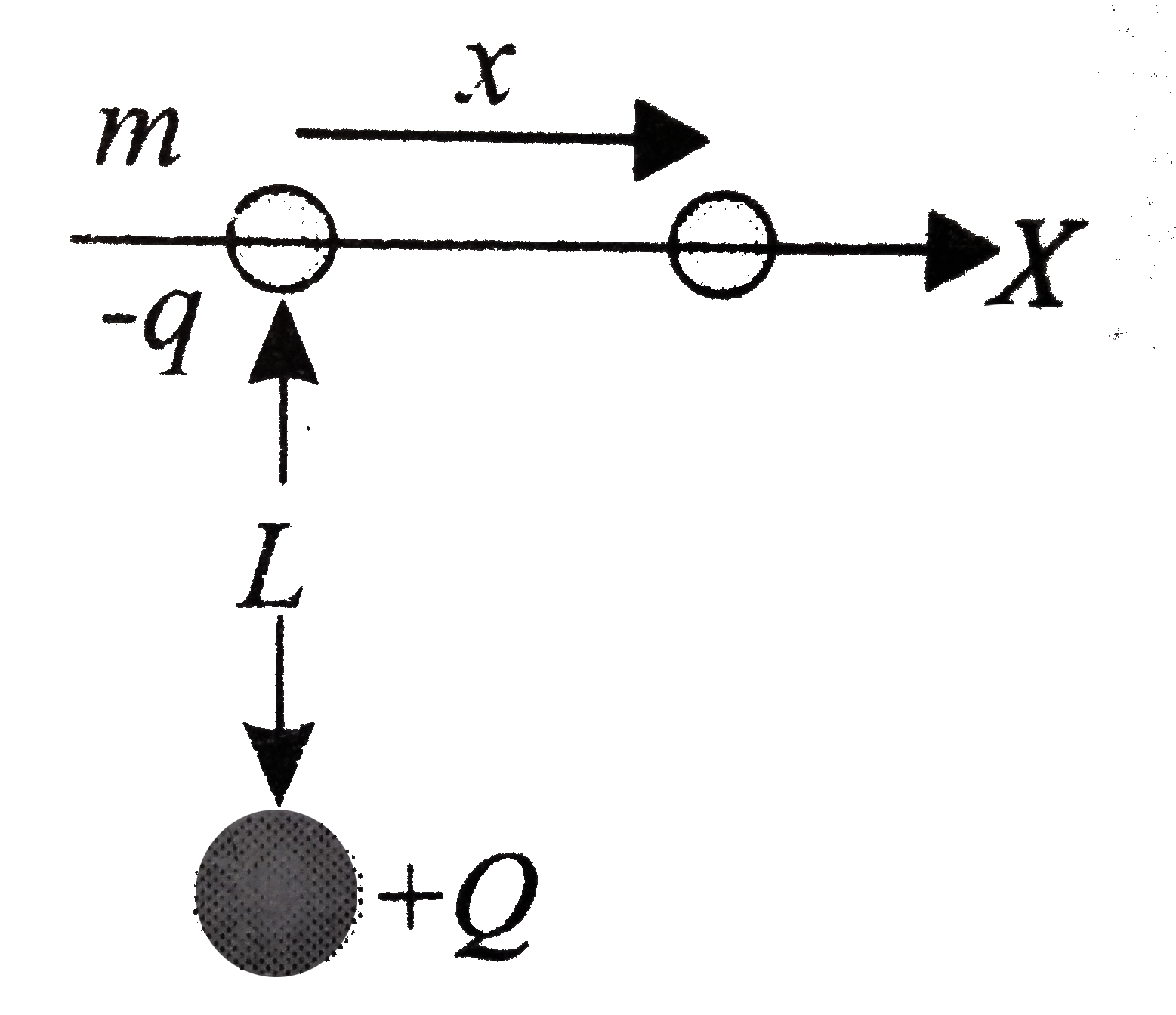
View SolutionA small beads of mass ma having charge -q is constrained to move along a froctionless wire. A positive charges Q lies at a distance L from the wire. Initiallym the bead is just above charge +Q. Show that if the bead is displaced a distance x, where `xltltL`, and released, it will exhibit simple harmonic motion. obtain an expression for the tive period of simple harnonic motion.
View SolutionA charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density `lambda`. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
View SolutionA point charge `Q_(1)=-125mu C` is fixed at the center of an insulated disc of mass 1 kg. The disc rests on a rough horizontal plane. Another charge `Q_(2)=125mu C` is fixed verically above the center of the disc at a height h=1m. After the disc is displaced slightly in the horizontall direction (friction is sufficient to prevent slipping), find the period of oscillation of disc.

View SolutionTwo small balls having the same mass and charge and located on the same vertical at heights `h_(1)` and `h_(2)` are thrown in the same direction along the horizontal at the same velocity v. The first vall touches the ground at a horizontal distance R from the initial vertical position. At waht heigth `h_(2)` will the second ball be at this instant? Neglect any frictional resistance of air and the effect of any induced charge on the ground.
View Solution
Subjective questions and complete solutions for chapter COULOMB LAW AND ELECTRIC FIELD of CENGAGE PHYSICS (HINGLISH) of Class 12