Complete Solutions to Comprehension of chapter COULOMB LAW AND ELECTRIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | COULOMB LAW AND ELECTRIC FIELD |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Two small identical conducting balls A and B of charges `+10 mu C` and `+30 mu C` respectively, are kept at a separation of 50 cm. these balls have been connected by a wire for a short time. The final charge on each of the balls A and B will be
View SolutionTwo small identical conducting balls A and B of charges `+10 mu C` and `+30 mu C` respectively, are kept at a separation of 50 cm. these balls have been connected by a wire for a short time
The final charge on each of the balls A and B and force of interaction will be
View SolutionTwo particles (free to move) with charges `+q` and `+4q` are a distance L apart. A third charge is placed so that the entire system is in equilibrium.
(a) Find the location, magnitude and sign of the third charge.
(b) Show that the equilibrium is unstable.
View SolutionTwo particles (free to move) with charges `+q` and `+4q` are a distance L apart. A third charge is placed so that the entire system is in equilibrium.
(a) Find the location, magnitude and sign of the third charge.
(b) Show that the equilibrium is unstable.
View SolutionThree charges are placed as shown in fig. the magnitude of `q1 is 2.00mu C`, but its sign and the value of the charge `q_(3) is +4.00muC`, and the net force on `q_(3)` is entirely in the negative x-direction
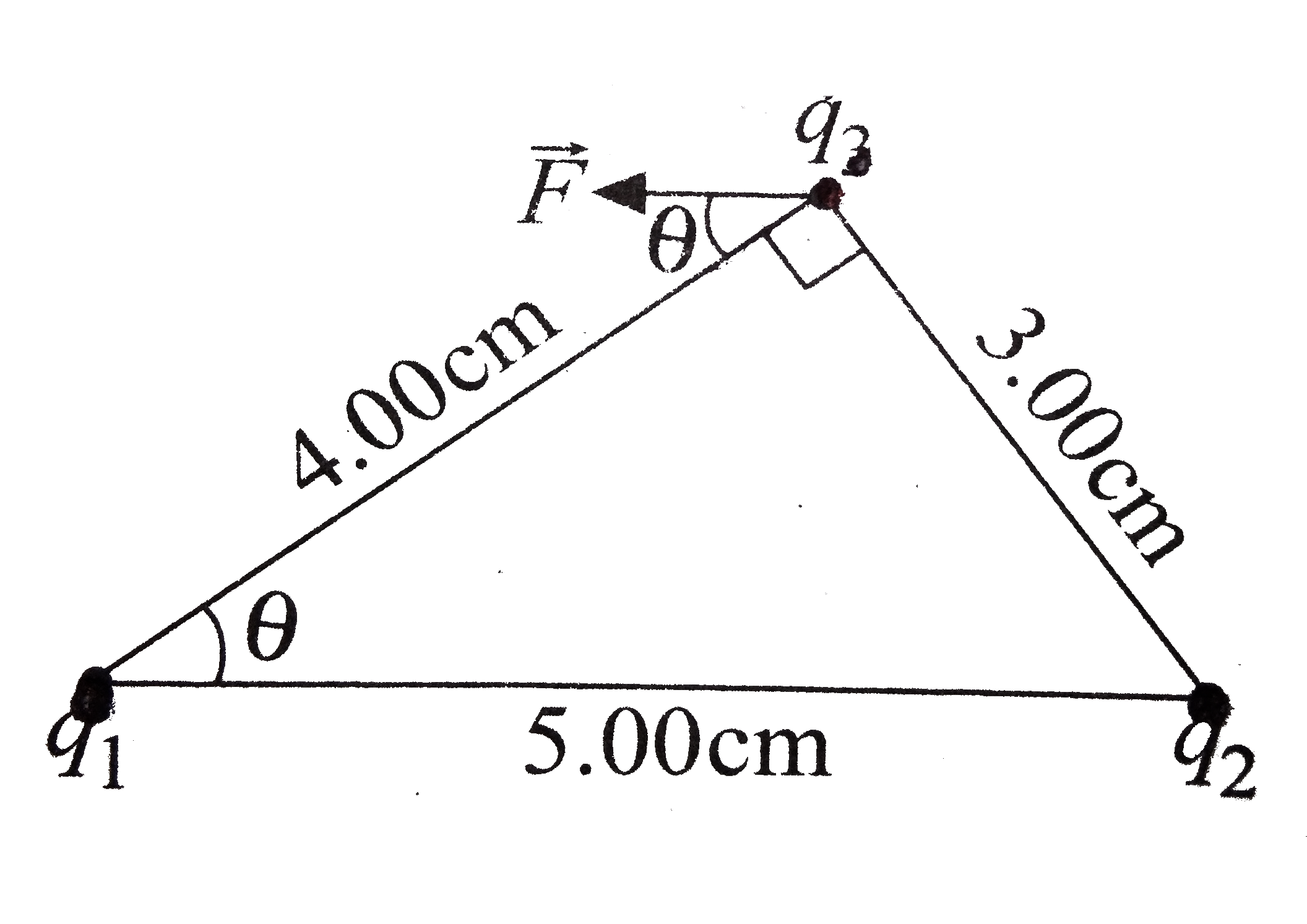
As per the condition given in the problem, the sign of `q_(1)` and `q_(2)` will be
View SolutionThree charges are placed as shown in fig. the magnitude of `q_(1)` is `2.00mu C`, but its sign and the value of the charge `q_(3)` is `+4.00muC`, and the net force on `q_(3)` is entirely in the negative x-direction

As per the condition given in the problem, the sign of `q_(1)` and `q_(2)` will be
View SolutionThree charges are placed as shown in fig. the magnitude of `q_(1)` is `2.00mu C`, but its sign and the value of the charge `q_(3)` is `+4.00muC`, and the net force on `q_(3)` is entirely in the negative x-direction

As per the condition given in the problem, the sign of `q_(1)` and `q_(2)` will be
View SolutionTwo point charge `Q_(a)` and `Q_(b)` are positional at point A and B. The field strength to the right of charge `Q_(b)` on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is `l=21 cm`.
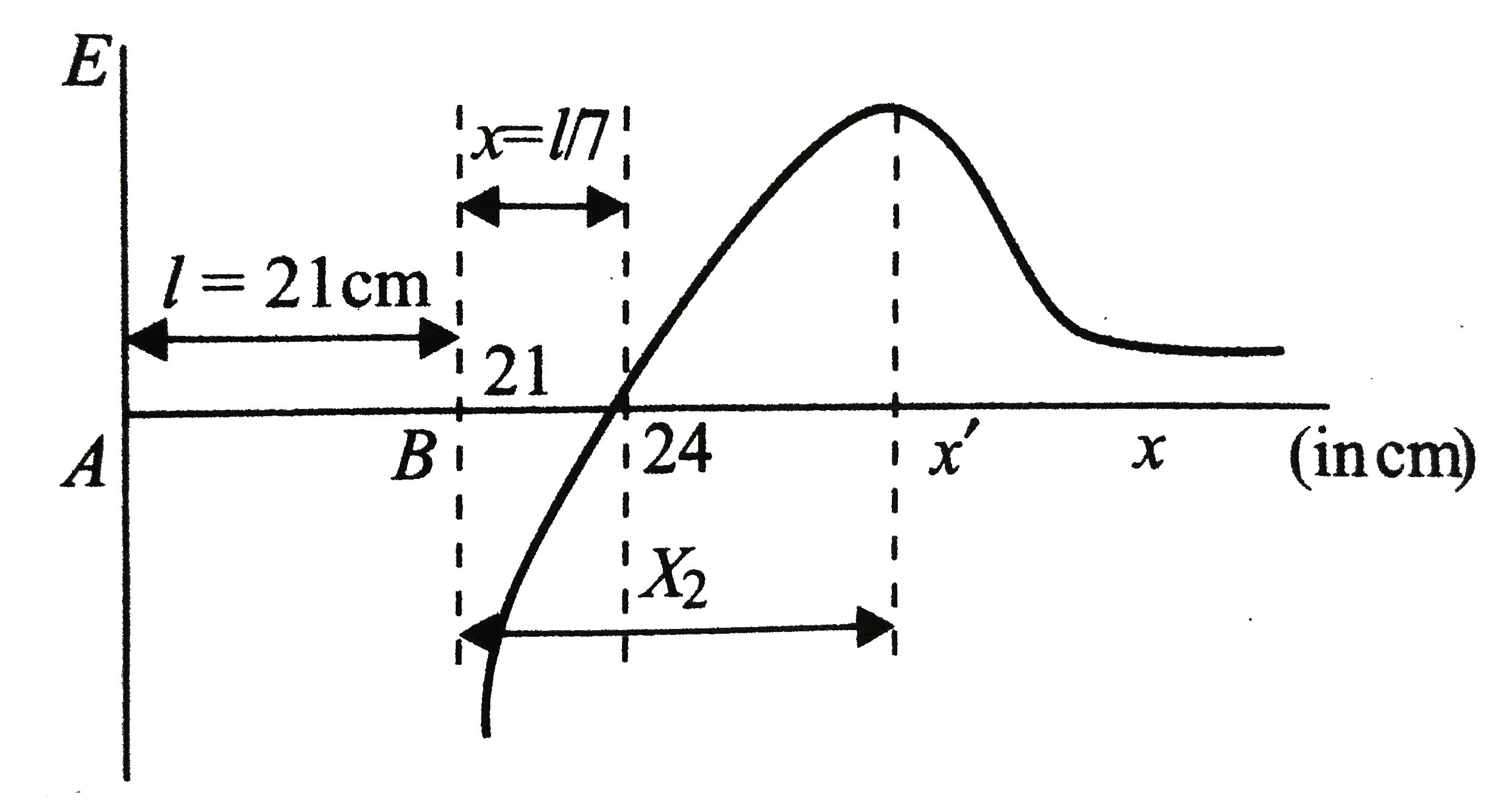
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge `Q_(a)` and `Q_(b)`.
(c ) Find the coordinate x of the point where the field strength is maximum.
View SolutionTwo point charge `Q_(a)` and `Q_(b)` are positional at point A and B. The field strength to the right of charge `Q_(b)` on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is `l=21 cm`.

(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge `Q_(a)` and `Q_(b)`.
(c ) Find the coordinate x of the point where the field strength is maximum.
View SolutionTwo point charge `Q_(a)` and `Q_(b)` are positional at point A and B. The field strength to the right of charge `Q_(b)` on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is `l=21 cm`.

(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge `Q_(a)` and `Q_(b)`.
(c ) Find the coordinate x of the point where the field strength is maximum.
View SolutionFour equal positive charges, each of value Q, are arranged at the four corners of a square of diagonal 2a. A small body of mass m carrying a unit positive charge is placed at height h above the center of the square.
What should be the value of Q in order taht this vody may be in equilibrium?
View SolutionFour equal positive charges, each of value Q, are arranged at the four corners of a square of diagonal 2a. A small body of mass m carrying a unit positive charge is placed at height h above the center of the square.
What should be the value of Q in order that this body may be in equilibrium?
View SolutionAn electron is projected with an initial speed `v_(0)=1.60xx10^(6)ms^(-1)` into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is `9.1xx10^(-31)kg`.
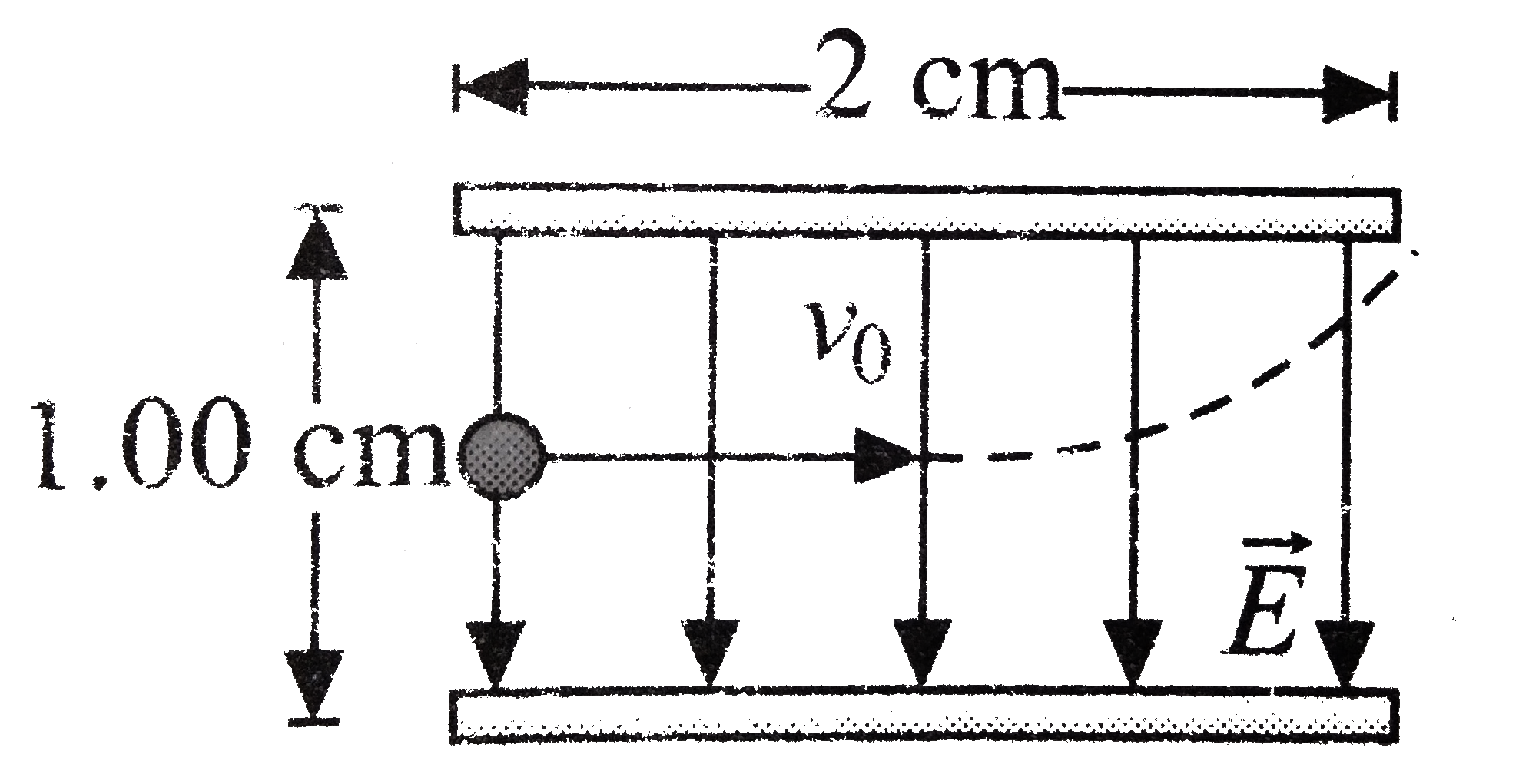
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is `1.67xx10^(-27)kg`).
View SolutionAn electron is projected with an initial speed `v_(0)=1.60xx10^(6)ms^(-1)` into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is `9.1xx10^(-31)kg`.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is `1.67xx10^(-27)kg`).
View SolutionAn electron is projected with an initial speed `v_(0)=1.60xx10^(6)ms^(-1)` into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is `9.1xx10^(-31)kg`.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is `1.67xx10^(-27)kg`).
View SolutionAn electron is projected with an initial speed `v_(0)=1.60xx10^(6)ms^(-1)` into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is `9.1xx10^(-31)kg`.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is `1.67xx10^(-27)kg`).
View SolutionAn electron is projected as shown in fig. with kinetic energy K, at an angle `theta=45^(@)` between two charged plates. Ignore the gravity.
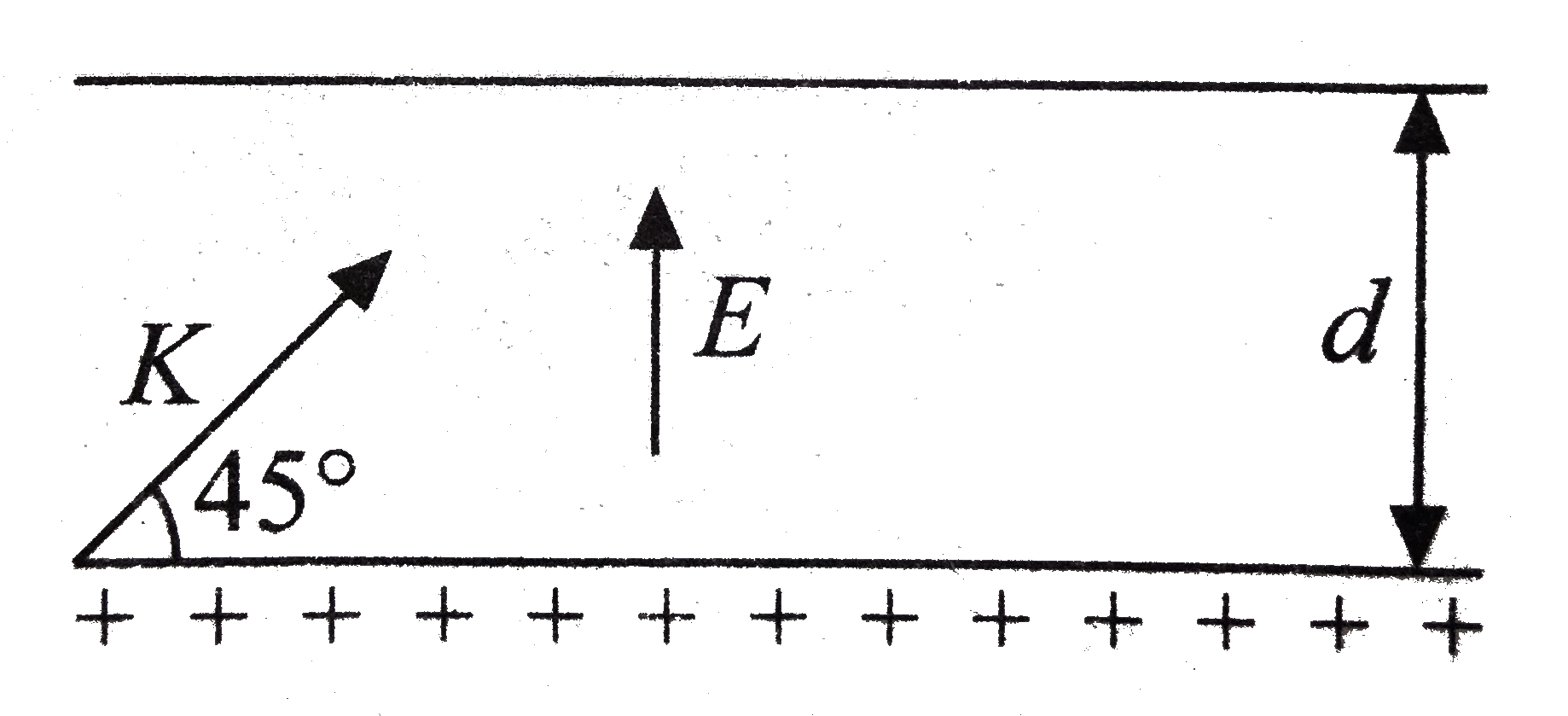
At what distance from the starting point will the electron strike the lower plate?
View SolutionAn electron is projected as shown in fig. with kinetic energy K, at an angle `theta=45^(@)` between two charged plates. Ignore the gravity.

At what distance from the starting point will the electron strike the lower plate?
View SolutionIn 1909, Robert Millikan war the firest to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were pbserved with a magnitue eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of `1.6xx10^(-19)C-` the charge of the electron. For this, he won the Nobel prize.
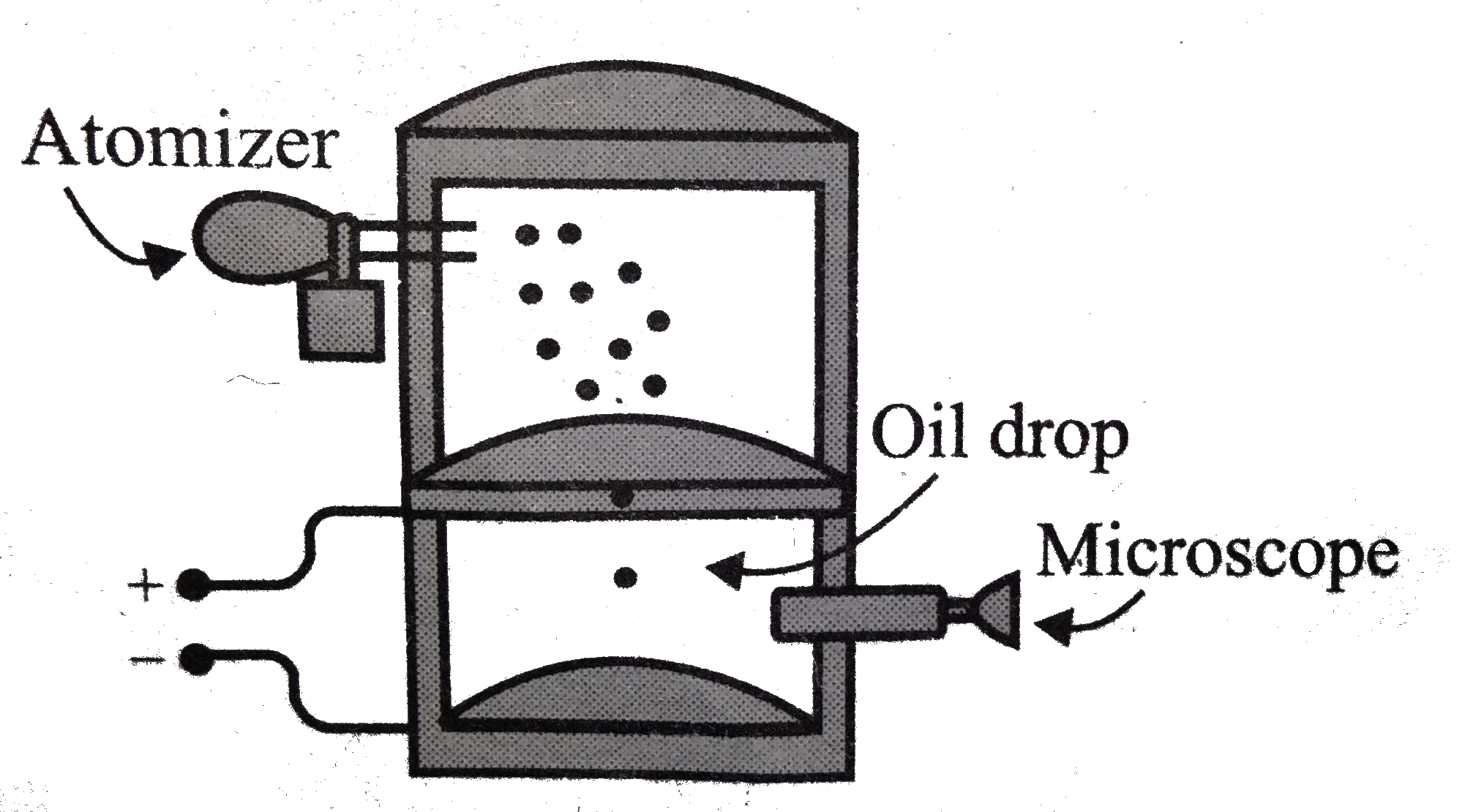
If a drop of mass `1.08xx10^(-14)kg` remains stationary in an electric field of `1.68xx10^(5)NC^(-1)`, then teh charge of this drop is
View SolutionIn 1909, Robert Millikan was the first to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were observed with a minute eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of `1.6xx10^(-19)C-` the charge of the electron. For this, he won the Nobel prize.

If a drop of mass `1.08xx10^(-14)kg` remains stationary in an electric field of `1.68xx10^(5)NC^(-1)`, then the charge of this drop is
View SolutionA simple pendulum of mass m charged negatively to q coulomb oscillates with a timeperiod T in a down ward electric field E such that `mggtqE..

If the electric field is withdrawn, the new time period
View SolutionA simple pendulum of mass m charged negatively to q coulomb oscillates with a time period T in a down ward electric field E such that `mg gt qE`.
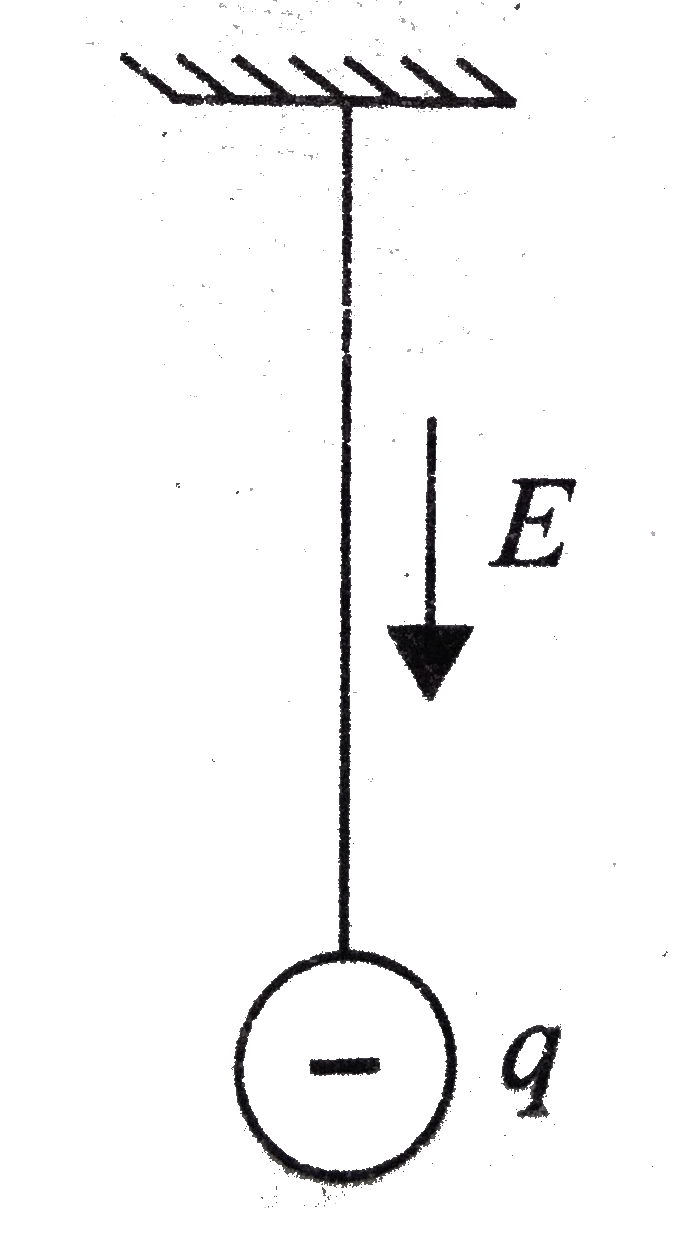
At equilibrium of he bob, the change in tension in the string will be (assuming rest condition)
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance `L//4` from one of its ends.
At first the rod is in unstabel equilbrium in a gorizontal umifrom electric field of field strenght E. Then we gently displace it from this position. Determine the maximim velocity attained by the ball taht is closer to the axis in the subsequent motion
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a distance `L//4` from one of its ends.
What is the time period of the SHM as mentioned in the above question, if an electric field `E` is applied along horizontal?
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance `L//4` from one of its ends.
What is the time period of the SHM as mentioned in the above question?
View Solution
Comprehension questions and complete solutions for chapter COULOMB LAW AND ELECTRIC FIELD of CENGAGE PHYSICS (HINGLISH) of Class 12