Complete Solutions to Exercise 3.2 of chapter ELECTRIC POTENTIAL of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL |
| CENGAGE PHYSICS | Exercise 3.2 |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
A particle of mass `1 kg` and charge `1//3 mu C` is projected toward a nonconducing fixed spherical shell of radius `r = 1 mm` having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
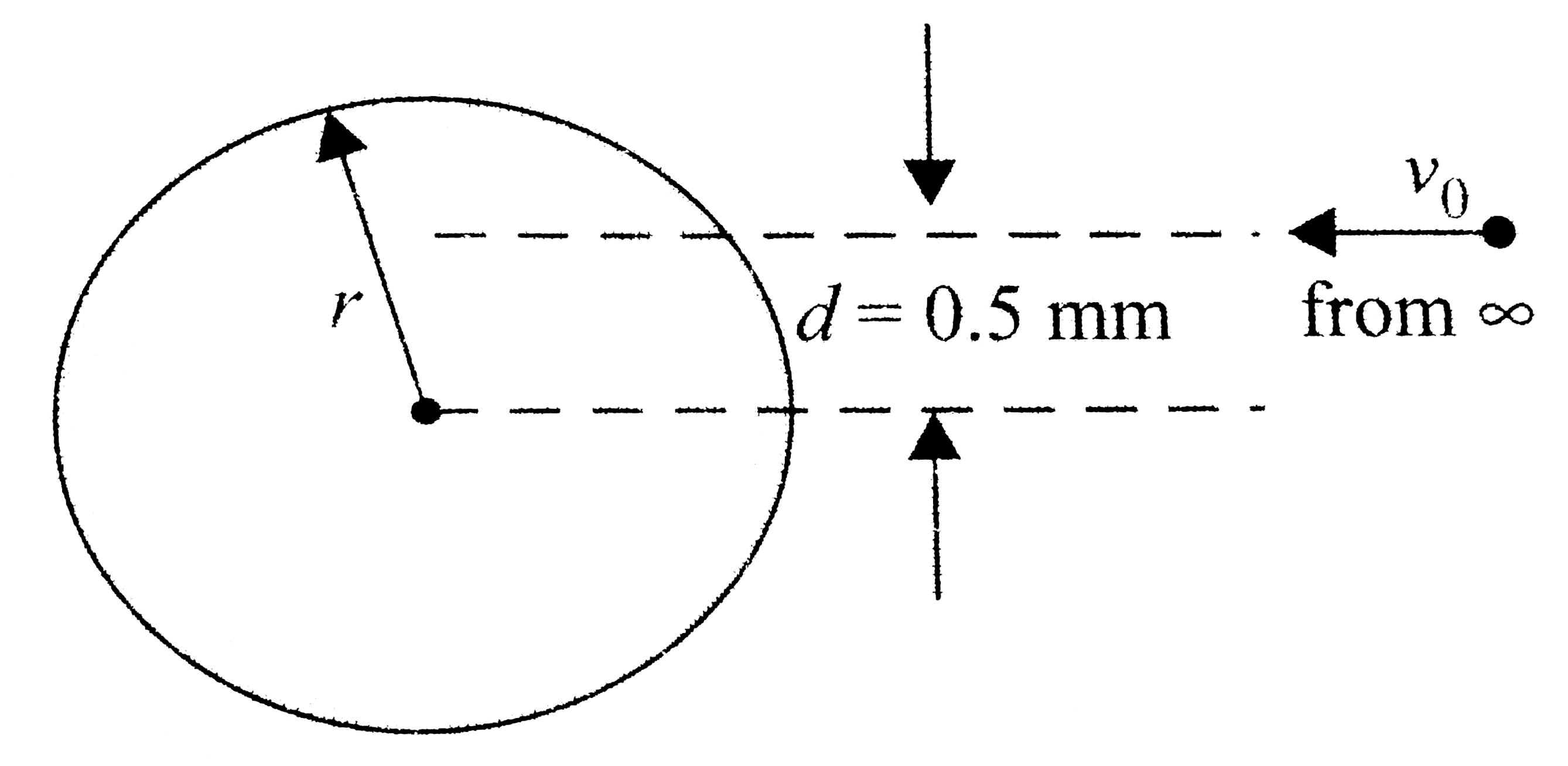 .
.
View SolutionA cone made of insulating material has a total charge Q spread uniformly over its sloping surface. Calculate the energy required to take a test charge q from infinity to apex A of cone. The slant length is L.
 .
.
View SolutionA simple pendulum of length `l` and bob mass `m` is hanging in front of a large nonconducting sheet having surface charge density `sigma`. If suddenly a charge `+q` is given to the bob `&` it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
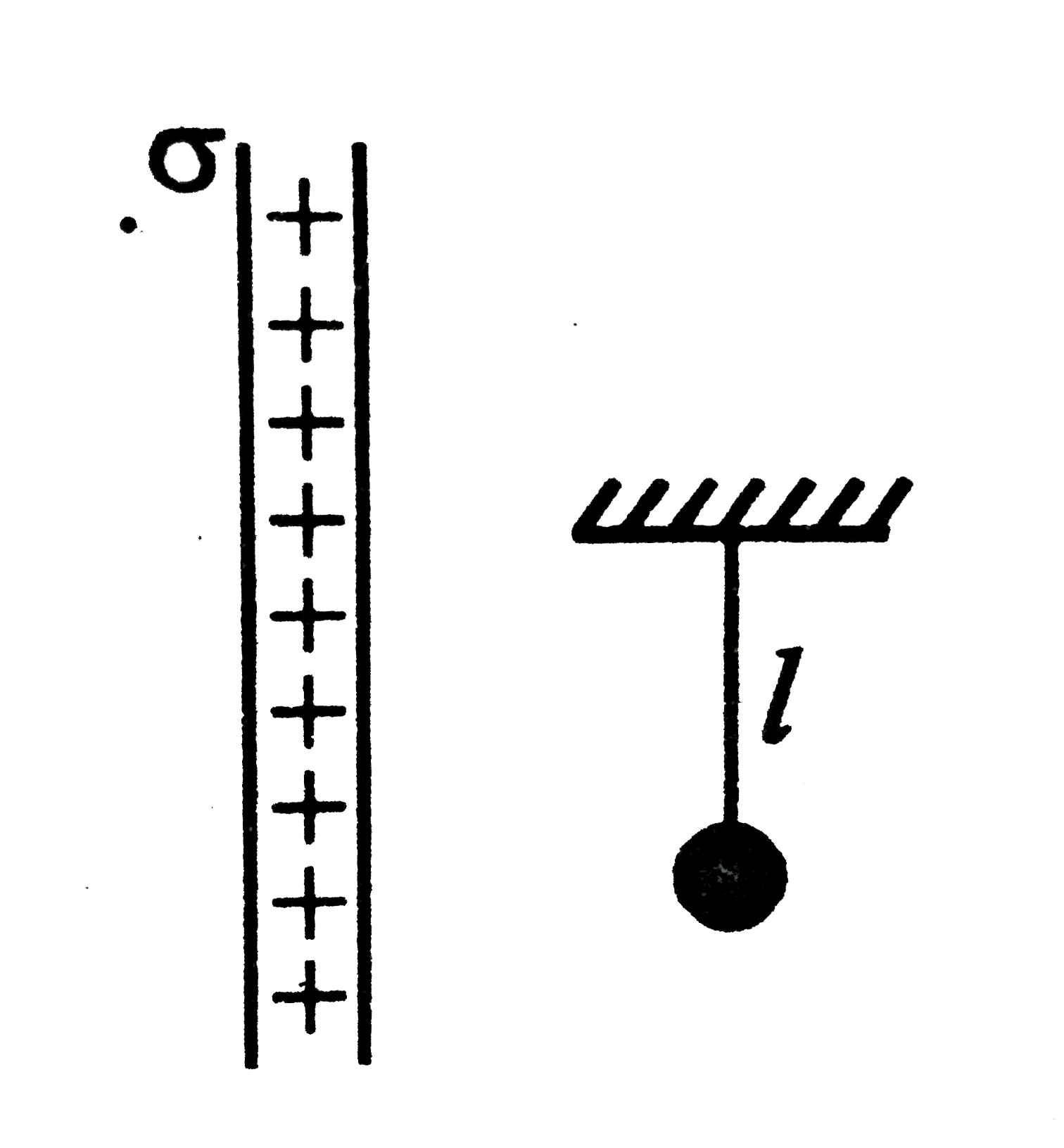 .
.
View SolutionAn insulating rod having linear charge density `lambda = 40.0 mu Cm^-1` and linear mass density `mu = 0.100 kg m^-1` is released from rest in a uniform electric field `E = 100 Vm^(-1)` directed perpendicular to the rod.
(a) Determine the speed of the rod after it has travelled 2.00 m
(b) How does your answer to part (a) change if the electric field is not perpendicular to the rod ?
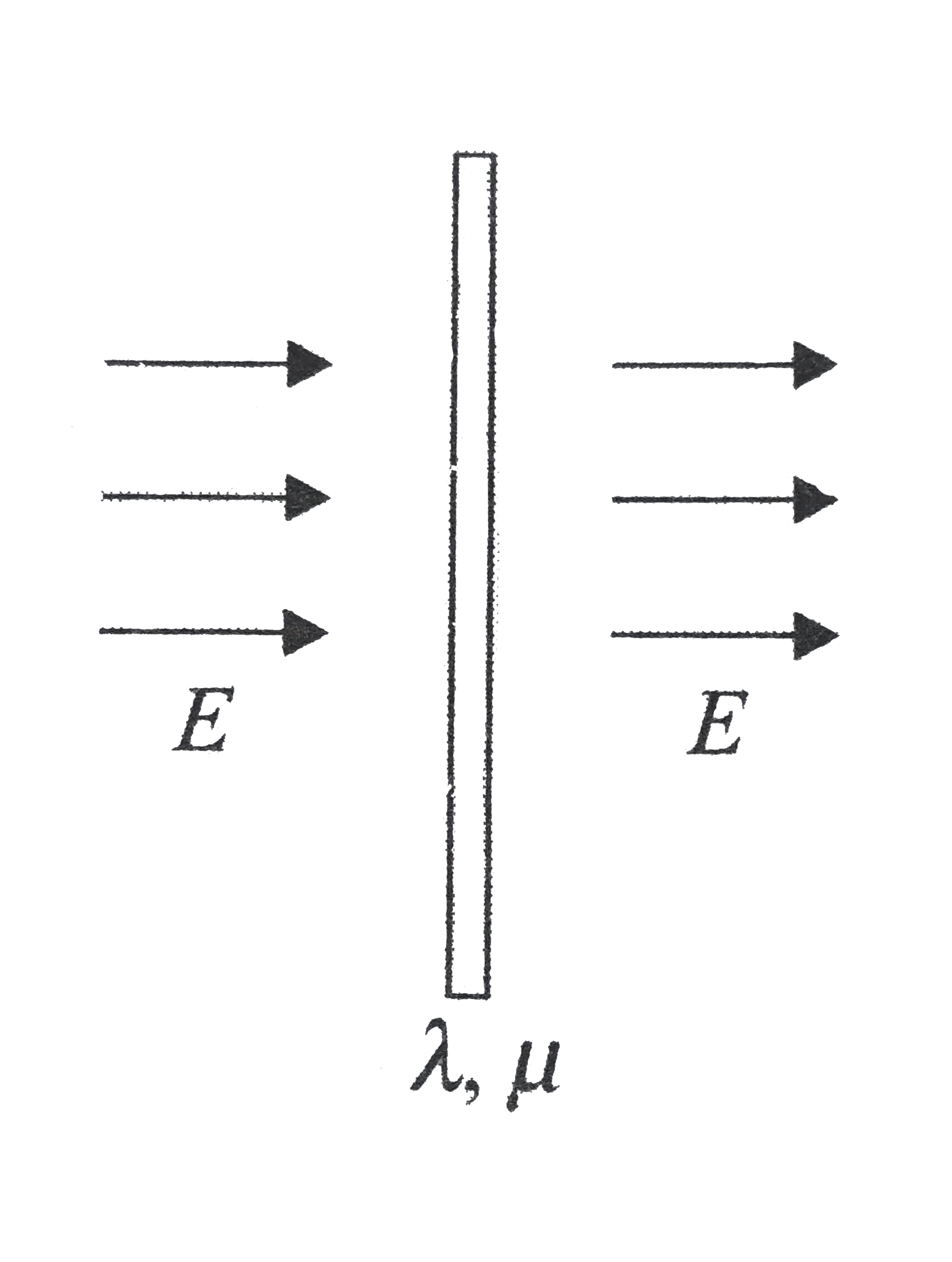
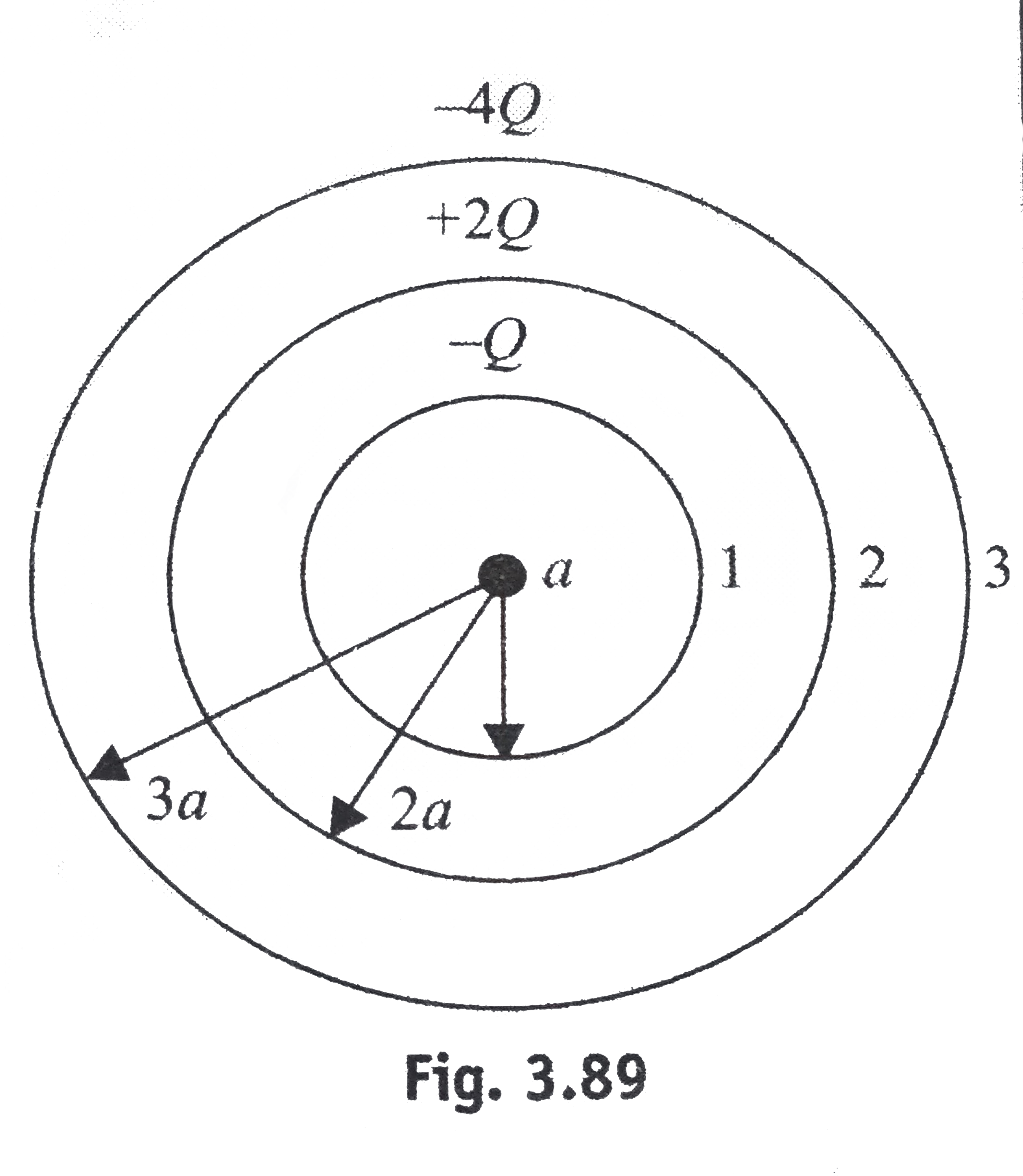
View SolutionThree concentric spherical conductors of radii a, 2a, and 3a have charges `-Q, +2Q`, and `-4Q`, respectively. If r is the distance of the point under consideration from the center of the spheres, then find the electric field and potential due to the given configuration, for the values
(i) `r lt a`
(ii) `a lt r lt 2a`
(iii) `2 a lt r lt 3 a`
`r gt 3 a`.
 .
.
View SolutionIn the previous problem, if we connect the conductors 1 and 2, 2 and 3, 1 and 3, 1 and ground, 2 and ground, and 3 and ground, separately, find the charge flown in each case.
View SolutionAs shown in, two large parallel vertical conducting plates separated by distance D are charge so that their potential are `+V_0` and `- V_0`. A small conducting ball of mass m and radius r `("where" R lt lt d)` is hung midway between the plates. The thread of length L supporting the ball is a conducting wire connected to ground, so the potential of the ball is fixed at `V = 0`. The ball hangs straight down in stable equilibrium when `V_0` is sufficiently small. Show that the equilibrium of the ball is unstable if `V_0` exceeds the critical value `[k_e d^2 mg//(4 R L)]^(1//2)`.

View SolutionElectrically charged drops of mercury fall from an altitude h into a spherical metal vessel of radius R. There is a small opening in the upper part of the vessel. The mass of each drop is m, and the charge on the drop is Q. What will be the number n of the last drop that can still enter the sphere?
View SolutionA small sphere of mass `m = 0.5 kg` carrying a positive charge `q = 110 mu C` is connected with a light, flexible, and inextensible string of length of length `r = 60 cm` and whirled in a vertical circle. If a vertically upward electric field of strength `E = 10^5 NC^-1` exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle `(g = 10 ms^-2)`.
View Solution
Exercise 3.2 questions and complete solutions for chapter ELECTRIC POTENTIAL of CENGAGE PHYSICS (HINGLISH) of Class 12